基于运动矢量的视频可逆隐藏算法
葛 京,杨红梅,2,颜 斌,谷玉莹
(1.山东科技大学 计算机科学与工程学院,山东 青岛 266590;2.山东科技大学 山东省智慧矿山信息技术重点实验室,山东 青岛 266590;3.山东科技大学 电子与信息工程学院,山东 青岛 266590)
常用的视频信息隐藏技术将视频视作多帧图像的叠加,并采用图像数字水印隐藏算法进行数据隐藏[1-2],虽然增加了隐藏信息的鲁棒性,但是受制于传统水印相对较高的算法复杂度,在现行的视频应用中并未有良好的表现。H.264作为常用的视频编码标准[3-4]是视频传输与存储的主要形式,结合编码标准的视频信息隐藏技术能更好的利用视频的编码特性,因此越来越多的算法开始利用视频的编码特性来进行信息隐藏[5]。
利用视频编码特性的视频信息隐藏技术一般包括视频空域和频域信息隐藏[6-8]与运动矢量信息隐藏[9],与视频空域和频域的信息隐藏研究相比,近些年基于运动矢量的信息隐藏研究工作相对较少,但这一类信息隐藏有其独有的优势,在应用中有着不可替代的作用。与空域和频域的视频信息隐藏算法相比,基于运动矢量的信息隐藏算法由于不改变视频参考帧和在传输中的运动矢量,通常较少遭受破坏,在解码端视频质量保障和隐藏信息保护方面均具有明显优势。在这一领域较早的研究工作是2001年Xu等[10]提出的压缩视频流中的信息隐藏算法(MVCA算法),将隐藏信息嵌入在绝对值大的分量中,利用较大数据允许更大变化的特点改变矢量进行数据嵌入。Fang等[11]提出了更符合矢量变化规律的相位角概念进行信息隐藏,之后Zhu等[12]利用1/4像素进行信息隐藏降低了矢量变化程度,苏育挺等[13]利用菱形算法进一步提高了嵌入强度。后期算法研究者又从局部最优性和相关性等方向开展了进一步研究工作[14-15],且更注重算法的安全性。但以上算法存在一个共同问题,就是在嵌入水印时会引起视频运动矢量的改变,而解码端无法消除这些改变所带来的影响。一方面,由于在解码端解码时无法利用传输的信息解码原始的运动矢量,因此算法只能利用改变后的运动矢量进行解码操作,会造成解码视频质量下降;另一方面,为了保证视频的质量,上述算法往往会利用嵌入信息后的运动矢量来进行残差运算,但是运动矢量的计算是在残差最小的情况下得出的,上述矢量信息隐藏算法中产生的运动矢量改变会造成残差码流的增加,影响传输效率。综上所述,如何能在解码端不借助大量的外部信息的同时还原未嵌入数据时的运动矢量信息隐藏算法成为迫切需要。针对这一问题,本研究通过在编解码过程中引入可逆信息隐藏算法思想来解决。
可逆信息隐藏算法早期是由Tian[16]针对图像提出的差值扩展算法,目的是在解码端提取隐藏数据并还原载体未嵌入数据时的状态,算法通过增加相邻像素值差值的最低有效位来实现数据嵌入,并利用差值扩展与变化的控制保证水印化图像的质量。在此基础上,Thoid等[17]提出了差值直方图平移的改进算法,解决了Tian算法中位置图占有大量比特信息问题,进一步提高了嵌入容量和嵌入后图像的质量。熊志勇等[18-19]也在这一领域进行了研究,实现了单向扩展和负数域的可逆算法来应对更复杂的情况。
本研究利用可逆信息隐藏思想可以无损回复原始载体的特性,设计了一种基于可逆思想的运动矢量信息隐藏算法。算法利用EPZS算法计算出目标运动矢量的最优预测矢量,通过调整预测矢量与目标运动矢量的差值实现水印嵌入,由于嵌入过程和提取过程引入了可逆信息隐藏的算法思想,在解码端提取完整的嵌入信息后可以还原最优预测情况下的视频运动矢量,较好解决了基于运动矢量的视频信息隐藏算法中嵌入数据导致运动矢量变化所带来的问题。得益于运动矢量完全恢复,在解码视频的质量得到保证的同时,避免了因为运动矢量改变所引起的码流增加和预测矢量改变所造成的GOP(group of pictures)误差积累。
1 最优预测矢量
当可逆信息隐藏算法在较大的待嵌入值中嵌入信息时,往往会产生嵌入后信息改变幅度过大的问题[16],对于运动矢量来讲同样会出现这种问题。而本算法采取在目标运动矢量与其最相关矢量的差值中进行嵌入的方案,以利用相关性使需要嵌入信息的矢量值较小。其中,找到与目标运动矢量最相关矢量的方法就是对当前的运动矢量进行估计。

图1 预测矢量选择
H.264提供了多种运动矢量的估计算法,本研究选用EPZS估计算法。EPZS算法包括运动矢量的预测选择、自适应提前终止和预测矢量的修正三大部分,是由Tourapis等[21]在2002年提出的一种基于PMVFSAST[20](predictive motion vetor field adaptive search technique)和APDZS(advanced predictive diamond zonal search)的矢量预测改进算法[21-22],旨在利用视频临近矢量的相关性减少预测矢量码流。将其用于本可逆算法中,可以提高运动估计的准确性,求得最优预测矢量,下面给出EPZS算法的三大部分。
1.1 预测矢量选择
矢量选择如图1所示,通过选择矢量构成集合A~C。
集合A={Median(MVTop,MVLeft,MVTop_Left)},其中MVTop为当前预测块上块的预测矢量,MVLeft前预测块左块的预测矢量,MVTop_Left前预测块左上块的预测矢量,Median为目标矢量取中值操作。
子集B={MVTop,MVLeft,MVTop_Left,MVPre,(0,0)},MVPre前预测帧前一帧与当前预测块位置相同块的预测矢量。
子集C={MVAcc,MVPre_Top,MVPre_down,MVPre_right,MVPre_left},MVAcc为包括加速度运动矢量的更复杂的运动预测矢量,MVPre_Top,MVPre_down,MVPre_right,MVPre_left为Frame(t-1)帧中与当前预测块位置相同块的四个相邻块的运动矢量。
1.2 自适应提前终止
自适应提前终止通过依次对集合A、B、C处理选择在预测范围内的预测模式来提高预测的速度。
设定T=a×min(Min1,Min2,…,Minn)+b,其中Min1,Min2,…,Minn表示邻块的最小匹配误差,a和b是依据运动矢量预测要求的设定值。依次遍历数据集A到C,运动矢量预测参差小于预测阈值T时,中止计算。
1.3 预测矢量的修正
当自适应终止不能满足阈值时,要进行进一步的矢量修正,以1.2小节选择的最优预测矢量对应的预测位置为中心,通过算法复杂度更高的模板,对预测矢量进行进一步的定位,以满足阈值,达到准确预测矢量的目的。
矢量预测完成后,得到了与目标运动矢量相关性极高的预测矢量,利用预测矢量可以减少运动矢量的冗余度,也为进行可逆信息的嵌入提供了与运动矢量相关性强的矢量。
2 矢量差值扩展隐藏算法思想
本算法核心思想是基于运动矢量的插值扩展,包括基于矢量预测的插值扩展、矢量失真控制、差值扩展标记和嵌入位置标记。
2.1 基于矢量预测的差值扩展
本算法将目标矢量的横向位移值与纵向位移分别与EPZS算法计算得到的最优预测矢量的横向位移与纵向位移做差,利用得到的差值来进行隐秘数据的嵌入。利用横向或纵向得到的差值进行嵌入与提取1bit数据并还原原始差值的过程示意图如图2所示,这样在解码端可以不需要通过外部信息来还原差值,从而可以通过解码的最优预测矢量还原原始的运动矢量。

图2 在差值中嵌入与提取1bit信息的示意图
通过改变嵌入差值的信息,可以实现在一个运动矢量中嵌入2n比特数据,n表示允许的扩展位。设目标矢量为MV(a,b),对应的最优预测矢量为MVP(a′,b′)。以矢量横向位移量a为例,定义矢量的差值(Dif)如式(1):
Dif=a-a′。
(1)
在计算机中,通过对矢量差值(Dif)左移n位,然后将待嵌入的n比特数据补位操作实现嵌入n比特数据bt,得到变化后的差值Difch:
(2)
其中,bin2dec是比特数据转十进制数操作,Difch为差值扩展改变后的差值。嵌入信息后的矢量横向位移量
(3)

(4)
提取嵌入信息如式(5):

(5)
其中dec2bin是十进制转比特数据操作,LSBn是提取目标最低n位有效值的操作。同理可以用同样的方法对b进行嵌入信息提取。
在解码端解码后,可以提取水印信息的同时还原原始矢量。
2.2 矢量失真控制
可逆的视频水印虽然在解码端可以无损恢复原始视频矢量信息,但是由于矢量的改变,非法解码端解码后视频质量会大幅度降低。当误差积累时,在一个GOP组中会导致明显的视频图像失真,从而影响信息隐藏的保密性。本算法对视频码流采取根据需要增加解码信息的隐蔽性方案,以提高算法在解码端的保密性。
根据人眼对运动剧烈的区域不敏感的特点,在视频运动剧烈的地方嵌入水印。解码端原始矢量在解码完成前不可知,无法利用原始的矢量值进行衡量。2.1节的算法未改变最优预测矢量的值,但最优预测矢量和当前块的真实矢量值具有强相关性,可以利用最优预测矢量来进行当前块的控制。具体方法是:对于预测得到的矢量,其运动程度可用式(6)进行计算。
(6)
其中H和V是预测运动矢量的垂直分量和水平分量,设定允许的阈值T′。当|MV|>T′时,标记为可嵌入块,否则,标记为不可嵌入块。阈值T′可以依据当前视频流的运动程度与需要进行嵌入的数据量进行设定,当需要嵌入的数据量较大且在非法的解码端质量要求较低的应用中可以采用较小的阈值,反之可以适量的增大阈值以保证算法在非法解码端的保密性。在解码端,利用解码前面完全恢复的矢量得到当前块的最优预测矢量,通过对比解码预测矢量的运动程度与允许的阈值T′,可以判断当前块是否为进行嵌入的块。
2.3 差值扩展标记
由式(2)可知,影响矢量改变程度的最大因素为目标矢量与最优预测矢量的差值,所以差值扩展运动矢量的变化程度依赖EPSZ算法的准确度,当运动矢量预测相对准确时目标矢量改变较小,反之则会使矢量偏移过大,引起解码端视频失真。因此,为了保证嵌入数据后的运动矢量与原始运动矢量不会有较大的偏差,引入差值扩展标记的概念。
在2.2节筛选出的满足失真控制的矢量中,提取相应的矢量MV(a,b)和最优预测矢量MVP(a′,b′),根据预测准确度的需要设定t作为预测阈值,通过式(2)得到差值与阈值t对比,设定差值扩展标记值mark:
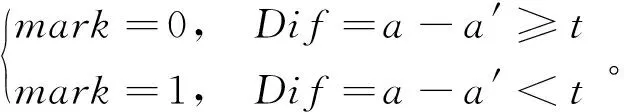
(7)
对b进行相同的操作,后续就可以利用mark的值来判断是否满足嵌入域值。
2.4 嵌入位置标记
由于在解码端无法知晓运动矢量是否进行过水印嵌入,因此为保证解码时辨别不同运动矢量的嵌入模式,需要将上述过程判断结果以码流形式保存,并作为水印与需要嵌入的信息同时嵌入到待嵌入视频中,据此,引入嵌入位置标记的概念。
首先,当前运动矢量满足2.2中的失真控制且横向位移和纵向位移mark值为1时,将矢量视为可扩展的矢量,其余的矢量视为不可扩展矢量。设定通过码流集合L来记录不可扩展运动矢量的最低有效位;对于可扩展的矢量进行2.1节中的扩展,并预留出可嵌入隐秘信息的n位最低有效置;对于不可扩展的矢量,提取差值的n位最低有效位,将提取出的最低有效位记入L中,并预留出可嵌入隐秘信息的n位最低有效位。依据次序对运动矢量进行标识,设定通过码流C来记录运动矢量是否为可扩展,当为可扩展时,记录当前运动矢量的标记码C为1,当为不可扩展时记录当前运动矢量标记码C为0。
这样得到各个矢量的嵌入位置标记C+L,对其进行JBIG2压缩或行程编码等无损压缩后作为隐藏信息传输。在解码端,只需提取每个运动矢量的n位最低有效位,就可以从中提取嵌入位置标记C+L,从而达到解码端对运动矢量是否嵌入数据可知的目的。
3 算法步骤
依据矢量差值扩展隐藏算法思想的嵌入策略,对待嵌入码流B实施的嵌入与提取过程分别在3.1节与3.2节介绍。
3.1 信息嵌入流程
本研究在H.264编码运动矢量时嵌入数字水印,信息嵌入具体过程如图3所示。
具体步骤为:
Step 1. 选定GOP组提取视频的运动矢量,得到选定块的运动矢量MV(a,b) ,并通过EPZS算法得到数字视频的最优预测矢量MVP(a′,b′) ,将两者做差得到运动矢量残差。
Step 2. 对选定块的运动矢量采取嵌入位置标记操作,区分可扩展和不可扩展的矢量,得到需要传输的位置标记C+L,并在不可扩展的矢量中预留可嵌入的最低有效位。
Step 3. 对可扩展的矢量进行差值扩展,并预留出可嵌入的位置。
Step 4. 获得待嵌入信息,转化为相应的二进制码流B,分别将二进制码流C+L与码流B进行JBIG2压缩或行程编码等无损压缩,再将压缩码流嵌入步骤2、3中已预留的可嵌入最低有效位。

图3 数字水印嵌入过程
Step 5. 判需要嵌入的隐藏信息是否嵌入完全,如若没有嵌入完全,引入下一帧进行上述过程直到所有信息嵌入完全。
3.2 信息提取流程
解码过程为编码过程的一个逆过程,过程如下:
Step 1. 找到选定的GOP组,提取嵌入帧的运动矢量。
Step 2. 得到选定块的运动矢量MV(a,b)与最优预测运动矢量MVP(a′,b′),提取两者差值的最低有效位,还原二进制码流C+L,提取并得到相应的嵌入位置标记,区分相应的可扩展的矢量和不可扩展的矢量,而后还原码流K=C+L+B。
Step 3. 对于不可扩展的矢量差值通过C+L中的位置标记和提取的码流信息,还原不可变化的运动矢量。
Step 4. 对于可扩展的矢量差值通过C中的位置标记信息,将差值行右移n位还原可变化的运动矢量。
Step 5. 计算下一块的运动矢量直到计算完毕,如果提取的码流B中没有停止的标识码流,继续对下一帧进行上述操作过程。
4 仿真实验与分析
以开源的H.264/AVC标准,利用Matlab进行仿真实验。实验使用了分辨率为 QCIF(quarter common intermediate format,176×144像素)的YUV视频序列的灰度分量,在JM11.0上,采取IPPP模式对6个运动状态不同的视频进行测试,包括Highway、Akiyo、Carphone、Coastguard、Suze与Stefan 6个运动序列。其中编码器为基线档次编码器、帧率为30 Hz、QP值为28、分辨率为176×144。
4.1 算法对于视频质量影响分析
对比算法为标准解码算法、文献[10]中的MVCA算法和文献[13]中的菱形算法,并在嵌入水印前进行残差的计算,以保证算法的解码端视频质量不受编码残差量的影响。分别对比变化平缓的视频组Akiyo和变化剧烈的视频组Highway。为了保证实验结果是在嵌入数据量相同的情况下产生,设定所有算法嵌入的数据量是视频编码中运动矢量数目的2倍,且三种算法对于矢量失真控制的阈值T′在相同的视频中设定的值相同。在不改变视频最优预测矢量计算的残差情况下对50帧中的运动矢量进行满嵌,通过依次比较提取数据后各个算法解码端解码的第n帧和标准解码的第n帧的视频质量来观察各种算法的性能。由于标准解码与本文算法解码后每一帧与原始视频PSNR值的折线图相同,因此不在折线图5与图7中表示标准解码的PSNR曲线,只在表1与表2中列出具体实验数值。
1) 对运动平缓视频进行算法性能实验分析
选取运动平缓的视频序列Akiyo,并给出标准解码与三种算法解码50帧后的图像和解码流程中的PSNR。
图4和图5给出了运动平缓的不同视频组解码端情况,从图中可以看出,所有的测试序列的帧在视频解码中都保持了和标准解码的帧基本相同的PSNR值,这是由于对于运动情况平缓的视频组来讲,视频运动不明显,运动矢量较小,使得矢量算法可以利用的矢量较少。在改变运动矢量少的情况下,算法均没有明显的视频质量变化,在视频解码对比中,几个算法均表现出了良好的特性。这一结果表明,本算法对于运动平缓视频进行信息隐藏能够很好的保证解码视频质量。
2) 对运动剧烈视频进行算法性能实验分析
选取运动剧烈的视频序列Highway,并给出四种算法解码50帧后的图像和解码流程中的PSNR。

图4 标准解码与三种算法解码50帧的视觉效果
图6给出了在运动剧烈的Highway视频流第50帧中解码端图像质量情况。在Highway视频组中解码两个对比算法视频图像中道路直线出现弯曲的情况,并且依据图7对比算法视频质量较差,这是由于MVCA算法和菱形算法中存在运动矢量的变化,导致了解码视频质量的下降。但本算法完全恢复了运动矢量,使得解码后的视频质量与H.264标准解码器解码的视频质量相同,因此本算法解码两组视频组后依旧保持着较高的解码视频质量。且从图7中可以看出,MVCA算法和菱形算法的PSNR会随着预测帧的增加而减少,这是由于误差的积累会使解码质量逐帧变差,从而导致了视频质量下降。由此可以看出本算法在视频解码质量方面优于MVCA算法和菱形算法,且这种优势随着GOP组中编码帧数的增加愈发明显。

图5 三种算法解码50帧的每一帧与原始视频的PSNR比较

图6 标准解码与三种算法解码50帧的视觉效果

图7 三种算法解码50帧中每一帧与原始视频的PSNR比较
表1给出了六个运动情况不同的视频解码第10帧与第50帧时的PSNR,通过六组视频序列的PSNR对比,可以看出本算法与标准解码算法的PSNR一致,均优于MVCA算法和菱形算法。
4.2 算法对于视频码流影响分析
为探究算法对于视频码流的影响,改变4.1节中实验的编码模式,在嵌入水印过程完成后再进行残差运算,保证在解码端视频质量下降只与残差的量化相关。实验通过控制嵌入量,同样使算法嵌入的数据量是视频编码中运动矢量数目的2倍,且三种算法对于矢量失真控制的阈值T′在相同的视频中设定的值相同。采用这种编码模式完整编码Highway、Akiyo、Carphone、Coastguard、Suze和Stefan的50帧,对比各个算法编码量。

表1 六个视频序列标准解码与三种算法解码的PSNR
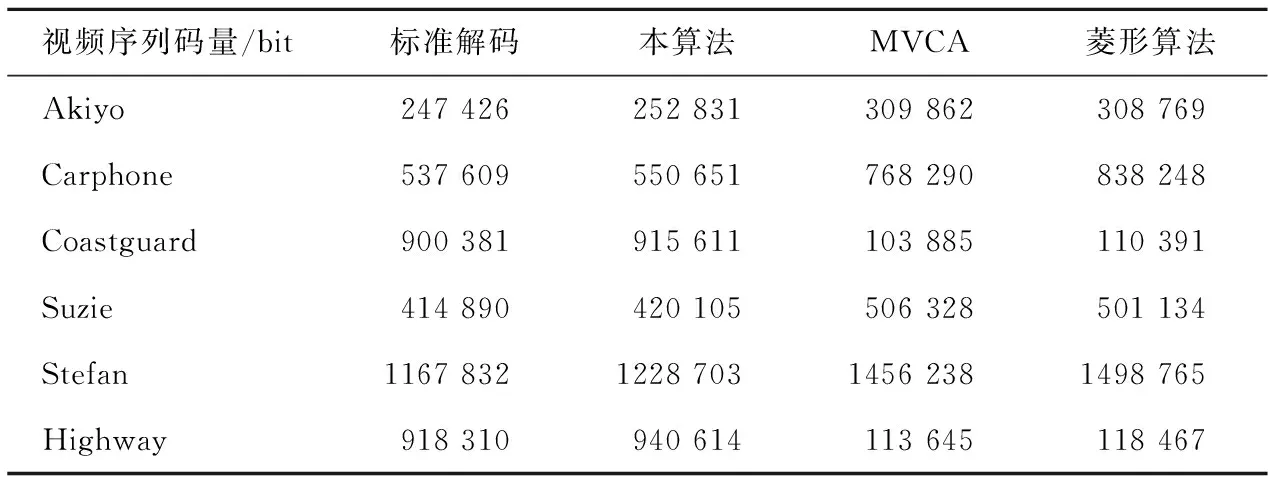
表2 六个视频序列标准解码与三种算法编码的码流大小
通过表2的实验结果发现三种算法在嵌入数据后与标准解码相比,码流有着不同程度的增加,其中本算法在同样嵌入强度时码量增加最少。产生上述结果的原因是本算法在解码端能够还原原始的运动矢量,使解码残差和标准解码算法的残差可以保持一致,且由于H.264中解码算法的残差是最优预测矢量下的残差值,残差值在编码过程中保持最小,编码后的残差的码流量保持最少。根据实验结果对比与分析,本算法对编码码流的影响均优于MVCA算法与菱形算法。
5 结论
利用可逆算法在解码端还原原始的矢量,确保了原始视频运动矢量的局部最优性,通过与MVCA算法和菱形算法在视频质量和编码码流的实验对比分析,可以看出本算法在加密信息的同时减少了码流的增加,并且保证了视频的解码质量,在运动剧烈的视频中优势更加明显。综上,本算法在解码视频质量和视频编码码流量方面均表现出高性能,在医学、法律与视频直播等领域具有广泛的应用前景。

