例谈课堂“错误”资源的有效利用
宋远征


【摘要】在课堂教学中,学生经常会出现各种各样的“错误”,这些“错误”也往往被教师忽视.本文以一堂“一次函数应用”复习课中学生出现的“错误”引发思考并生成新方法的过程为例,“错误”不仅不可怕,我们还要迎“错”而上,感悟数学的本质.
【关键词】课堂教学;错误;生成
学生解决问题的过程是一个不断试错的过程,这些错误包括审题、思维过程和运算等方面出现的错误.其中,有些“错误”也许会成为课堂的生成性资源,为解决问题提供了另外一种策略.学生的经验包括日常生活经验、社会生活经验、数学活动经验等.数学教学活动是以学生已有的经验为基础的主动建构的过程,杜威就曾指出,学生的经验是教学的起点.因此,在试错的过程中根据每名学生个体经验的不同,从问题的切入到最终解决的路径会有所差异.作为一名数学教师,在课堂上要不断引导学生依据不同的情境,采取不同的策略对学生的经验进行辨别、改造和提升,从而达到认识数学的本质的目的.
著名学者弗赖登塔尔说过,学习数学的唯一正确的方法是“再创造”,让学生把想要学的东西去自己发现或创造出来,教师的任务是引导学生进行这种创造工作,而不是把现成的知识灌输给学生.下面通过一名学生在审题时将题目的条件读错从而引发课堂上的一系列的交流与思考.
一、“错误”生成
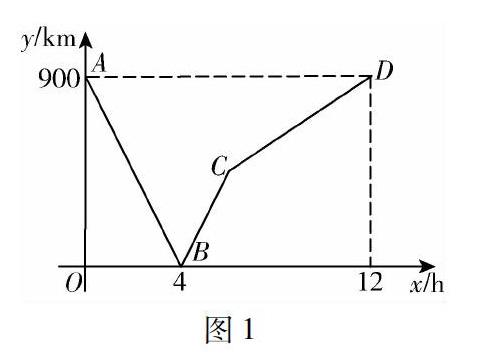
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图1中的折线表示y与x之间的函数关系.问题解决:若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.在第一列快车与慢车相遇30分钟后,第二列快车与慢车相遇.求第二列快车比第一列快车晚出发多少小时?
(题目已经做了简化,只保留了最后一问,前面4个小问是分析图1中的数量关系与各直线所表示的实际意义,较容易解决,也为解决最后一问提供必要的条件)
分析与思考 将图1的行驶状态用图2来表示.快2与慢车相遇的时候,快2与快1之间的距离差正好等于快1与慢车的距离差.快1与慢车的距离差是在快1与慢车相遇之后产生的,因此,这个距离差可以用速度和乘时间来表示,即225×0.5=112.5(km),所以快1与快2的时间差为112.5150=0.75(h),这个时间差就是快2比快1晚出发的时间.
这是学生2学习了前面学生1的“错误”经验,在学生1正确画出图2的基础上计算出来的结果.而学生1在正确画图之后,在列方程的时候一直处于“卡壳”的状态,因为他一直在把两列快车当作同时出发来做,无法列出正确的方程.
二、教学片段
此时,笔者的想法是不直接指出学生1思考中的错误,而是采取了追问引导的方式,提出了一个问题:“如果以快1和快2同时出发作为条件,算一算结果会怎样呢?”
学生3在思考片刻后,大胆举手,说出了他的想法:假设快1和快2同时出发,且快2的速度比快1慢,根据图2,快2与慢车相遇用了4.5(h),根据总路程相遇时间=速度和,即9004.5=200(km/h),则快2的速度为200-75=125(km/h),用150×4.5-125×4.5=112.5(km/h),再用112.5÷150=0.75(h).
这名学生当时并没有给出合理的解释,笔者决定继续花时间与学生一起重新从这名学生的角度来审题.
教师:“我们先换个角度思考,先从答案的角度逆向思考,已知快2晚出发了0.75(h),大家算一算快2在4.5(h)内的平均速度,你有什么发现?”
学生4:“我算的是0×0.75+150×3.750.75+3.75=125(km/h),正好與之前假设两列快车同时出发时的快2的速度相等.”
教师:“因此,我们可以把这个快2的速度125(km/h)理解为快2在4.5(h)内的平均速度.再把思路切换回来,我们已经假设了快2的速度与快1相同的,但是实际上这里快1与快2经过4.5(h)后出现了路程差,那我们如何理解这个路程差呢?”
学生5:“这个路程差本质上是由快2晚出发的时间来抵消的,即150×4.5-125×4.5150=0.75(h).”
三、课后反思
在课堂教学中,教师经常受到时间的制约,特别容易忽视“错误”,常常采取的办法是反驳学生的“错误”,引导他走向所谓的正确的路径上,殊不知,这让学生失去了一次宝贵的主动思考和交流的机会.
数学教学活动要把握数学内容的本质,创造合适的教学情境,提出合理的问题,启发学生独立思考,鼓励学生与他人交流,让学生在掌握知识技能的同时,感悟数学的本质,让学生积累数学思维的经验.学生所学习的数学知识都是前人已经建造好的,但学生需要亲身参与到教学过程中去感悟,才能体会数学中丰富、生动的概念和思维活动的组织过程,学生的“错误”也是自身思维活动中的一种“创造”.教师如果能引导学生深入探究,从正向到逆向或者从特殊到一般,让学生不局限于一种思维模式,培养学生发散的思维.
在课堂中,教师与学生之间进行思维上的碰撞,在试错的过程中,师生围绕这些意外产生的问题思考和讨论,学生在成长,教师在反思,这才是数学课的魅力所在.
【参考文献】
[1]许冬梅.浅谈初中几何数学中发散思维的训练[J].数学学习与研究,2019(11):34.
[2]史宁中.学科核心素养的培养与教学——以数学学科核心素养的培养为例[J].中小学管理,2017(1):35-37.

