基于前概念修正的小学数学概念教学探讨

摘 要：学生头脑中比较顽固的前概念在有些老师看来是影响新概念建立的障碍，但换个思路，它正是教学的出发点。立足于前概念，使之充分暴露出来，经过教师不断的引导，慢慢推着它向新概念移动，最终实现前概念的修正而建立新概念。

关键词：小学数学;前概念;同化;修正

数学概念是数学思维的基本形式。所谓“基础不牢，地动山摇。”牢牢抓住概念教学这一基石，数学教学质量才有望大幅度提高。在现行的数学课堂中，老师们比较重视计算法则、解题方法的指导，却普遍忽视数学思维能力的培养，尤其把概念看作“小儿科”不加重视。当前，有的老师过度重视故事情境的创设，却没有对教材本身的逻辑体系进行深入研究，导致学生头脑中建立的概念互相抵触、莫衷一是，最终在解决实际问题时只能凭感觉行事，错误不断。

一、 关于前概念修正的理论认识

（一）建构主义心理学视野下的概念教学理念

建构主义心理把相对于新概念而言学生先前已经具备的经验被称为“前概念”。在前概念的基础上进行教学，通过学习不断的同化与顺应，可以尽快实现科学概念的构建。

所谓“同化”，是指前概念与新概念之间有较多相似成分，学习者只需在前概念中增加原来没有的新异信息，将新概念趋同性地纳入原有概念之中就可以了。比如学习“三角形”这个概念之前，有学生认为：三角形有三个角，这每个角应该都是锐角。这一认知是印象式的，学生往往能在后续的学习中自动修正错误。

所谓“顺应”，是指前概念与新概念之间存在较大差异，此时前概念必须尽大力修正原有错误，才能达到内心的平衡。人都有惰性，当“愚公移山”不易办到时往往选择“阿Q精神”，以保持原有平衡状态。比如学习“甲数的3倍等于12，求甲数是多少”时，不少学生存有顽固的“倍即是乘”的观念。此时基础相对薄弱、不肯动脑的学生往往会忽视老师的指导，似乎也能自得其乐。

（二）概念教学的优化方向

“同化”与“顺应”过程所需要花费的力气是有区别的。打个类似的比方，把一个优秀的少先队员培养成优秀共青团员较之把一个少年犯培养成一个优秀共青团员，其难度决然不同。当然，一个优秀的思想工作者在做少年犯的工作时，他可能会蹲下来与对方目光平视，设法与对方拉家常，甚至故意暴露自己的一些劣迹来打动对方，这其实就是遵循了尽量同化的原则。具体落实到概念教学中，我们应尽可能地让学生去同化，即使采取顺应策略，也应设法求同存异，使他有理由把新旧概念联系起来。

二、 以“三角形的高”为例进行概念教学策略探讨

学生对于概念产生偏差一般分为两种情况：一种是易矫正型的概念偏差，另一种是顽固不化型的概念。我们有必要探讨第二类概念的教学，比如“三角形的高”就涉及与高与底的关联性，每个三角形有三条不同方向的高，而且存在形外高的情况，是小学阶段概念教学中的一大难点。以下就此展开探讨：

（一）预热前概念——找找生活中的高

1. 房梁与身高

师：房屋的人字形房梁的形状是三角形（图1（1）），请大家思考：（1）如果要量出房梁的高，应该从哪里量到哪里？（2）这条表示房梁高的线段与下边的这条长边是什么关系？

师：（指较短的一条竖向线段）为什么不去量这一条呢？

生：因为它并不是最高的，整个梁最高的位置应该是在大三角形正上方的顶点。

师：是啊！这就像我们在测量身高的时候，都是从头顶量到脚底，而不是从肩膀量起。

分析：由学生熟悉的事物引发探究，正是基于学生平时对“高”的理解：比如“这山好高啊！”是一个形容词，再如“小明高150cm。”是一个名词。“三角形的高”也是名词，但又有严格的定义，指特定的线段。但上述三者又存在引申关系：他们都与竖向有关，都有与水平线垂直的含义，能把它们放在一起理解就是顺水推舟的事。也正是这个原因，一开始呈现三角形高垂直于水平方向底边，这具备了概念的雏形，为后续的“四面出击”建立了“根据地”。

2. 一根垂挂的绳子

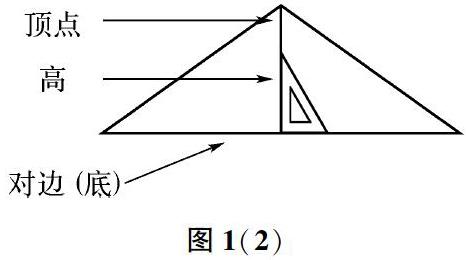
师：现在，我们把这个三角形画下来，从三角形的这个顶点向它的对边所在直线可以作一条垂直的线段，这条垂直线段就是三角形的高，而这条对边是三角形的底。（图1（2））

师：我们再来看这个图（图2），图上的三角形表示的是一张帆，你能过最上边那个顶点给这个三角形画一条高吗？假如现在只有一条绳子，你能用这条绳子来代表高吗？你还见过类似这样绳子的事物吗？（学生联想到：吊车的巨臂下挂的钢索，山岩下的冰凌）假如现在帆张得更开了（图3），你能重新画一下刚才那条高吗？

分析：很多概念是劳动人民把生活体验上升到数学智慧的结果。这一步教学假定三角形高的原始概念为：过一边水平摆放的三角形物体的最高点向对边所作的垂直线段。这样的表述更合乎人类生活实际，与学生的前概念也更接近。这两个图都突破了锐角三角形的限制，为直角三角形、钝角三角形作高提供了原型。教学到这一步，学生的前概念又有了新的延续：高是与水平方向的底边垂直的。

（二）发展前概念：画同一个三角形的高

师：现在同学们手头的练习纸上有这么一个三角形，请你分别画出不同底上的高，再说说你是怎么画的。

师：图4（2）的底是斜放的，我们能让它变水平吗？

生3：底斜放的时候，可以把图转过来，让底变成水平。（教师用视频演示，然后师生得出画高方法“一平二挂三畫”）

生4：我看不转也可以，这就是以前学过的画垂线的方法啊！

师：对，这类似于以前学过的过直线外一点画这条直线的垂线，不同的是高是一条线段。所以大家可以不看三角形的另两条边（用虚线标示），直接过顶点画与对边直线垂直的线段。（图4（6））

师：（针对图4前三个图）现在我们发现三角形的每一条底都有与它对应的高，这就好像一把钥匙开一把锁一样。细心的同学会发现，这三个三角形其实完全一样，我们把它重合在一起（视频演示）就会发现什么？

生：一个三角形有三条高，三个底，每条高对应一个底，这条高与底垂直。

分析：让学生自己画同一个三角形的三条高，教师着重就画斜向边上的高提供引导：①“一平二挂三垂足”。这里的“一平”指的是把底旋转或者想象成水平的。“二挂”类似于吊车顶上的钢索，须从顶点出发与底边垂直。“三垂足”指的是所画高到垂足后不再伸展。这就将画不是水平底上的高纳入作水平底上的高的体系之中，很快产生同化作用。②过直线外一点画已经直线的垂线段，教师提供图画的原型，这又使学生把新知识纳入旧知识之中，从另一个角度实现了思维同化。

显然，这一步教学丰富拓展了前概念，学生对生活中的高的理解已經较为完善，前概念已经前进到新概念的“门口”。

（三）修正前概念：画不同的三角形的高

师：请三位同学来画一画老师指定底上的高。

师：现在我们来看芳芳同学画的三条高，对吗？错在哪里，需要怎么纠正？（图5）

分析：由于教师在前几步中做足了前概念同化的准备，所以这时的引导变得较为容易，学生能较快地画出特殊情形下的高。纠错练习在这里起到了提醒学生顶点、高及底边所在的直线三者之间关系的作用。在无声无息中，新概念已经悄悄浮出水面。

（四）建立新概念

下图（图6）每一小方格面积为1cm2，以图中 5cm 长的线段为底，用直尺直接画出高是3cm的三角形（尽量多画）。

分析：通过开放式答题，使学生能从上下两个方向，分在格点上与不在格点上两种情况，找到不同类型的三角形，使三角形高的概念经过不断的操作牢固地掌握起来。这一题的设计改变了已知三角形作高的传统命题方法，使学生耳目一新，同时摈弃了题海战术，将多种知识融合于一炉，有助于学生对三角形高的知识体系进行分类回顾与系统建构。至此，原有的前概念已经消失，新概念已经取而代之。

总之，对于容易出错的新概念的教学，我们应尽量激活学生头脑中的前概念，使之充分暴露出来，经过教师不断地变化引导，慢慢推动它向新概念靠近，最终实现前概念的修正而建立科学有效的新概念。“山不过来，我就过去。”概念教学理应有扎根生本的勇气，才能带领学生走得更远。

参考文献：

[1]沃建中.小学数学教学心理学[M].北京教育出版社，2001.

[2]毕宏辉.迷思概念的诊断与教学转变策略——以“三角形的高”为例[J].中小学数学（小学版），2016（Z1）.

作者简介：

顾琴芳，浙江省绍兴市，浙江省绍兴市柯桥区鉴湖小学。