4个阔叶树种树高曲线模型的研究

武文昊

（辽宁省林业调查规划监测院，辽宁 沈阳110122）

树高和胸径是森林调查中最重要的因子［1-2］，与胸径相比，树高的测量比较困难、费时，且相对复杂，鉴于这种情况，在目前的森林调查和试验研究中，常常只测量部分树木的树高，缺失的树高则通过不同树种的树高-胸径模型来预测［3］，树高曲线的拟合就是这种关系的表现形式。树高曲线是建立生长与收获模型的基础［4-5］，还可用来预测树木材积，计算优势木高和立地指数，最终用于描述林分生长动态和演替［6］

关于树高-胸径模型，国内外有大量的相关研究，比如国内有大量关于杉木Cunninghamia lanceolata、马尾松Pinus massoniana、云杉Piceasp.等树高曲线的研究［7-9］，而关于东北天然次生林中阔叶树种树高模型的研究较少。因此，本研究以辽宁宽甸泉山林场天然次生林为研究对象，以常见的17个树高曲线模型，对核桃楸Juglans mandshurica、黄波罗Phellodendron amurense、枫桦Betula costata和灯台树Bothrocaryum controversum筛选最优的树高曲线模型，为该区域开展森林资源调查和次生林结构调整等方面的研究提供理论基础。

1 研究区概况

泉山实验林场位于辽宁省宽甸县东北部，林场地处长白山脉龙岗支脉的延续部分，其地理坐标为124°54′～125°21′E，40°55′～41°09′N，总 经 营 面 积1 401.5 hm2，海拔400～1 200 m，属辽宁东部中低山地。属温带半湿润季风气候，年平均气温6.5 ℃，年平均降水量1 100 mm，雨量多集中在每年的7、8 月份，年平均蒸发量1 129.1 mm。森林土壤主要为棕壤，土壤质地多为沙壤质，且土壤含砾石较多。林场属长白植物区系与华北植物区系的交错地带，基本上属红松阔叶混交林植被带，现在以天然次生林为主。主要针叶树种有红松Pinus koraiensis、日本落叶松Larix kaempferi、长白落叶松Larix olgensis、云杉等；主要阔叶树种有辽东栎Quercus liaotungensis、枫桦、核桃楸、黄波罗、灯台树、水曲柳Fraxinus mandschurica等；主要灌木有胡枝子Lespedeza bicolor、忍 冬Lonicera japonica、卫 矛Euonymus nanoides等；主要藤本有狗枣猕猴桃Actiniaia kolomikta、山葡萄Vitis amurensis、五味子Schizandra chinensis等；主要草本有堇菜Viola verecunda、水金凤Impatiens noli-tangere、悬钩子Rubus crataegifolius等。

2 研究方法

2.1 资料收集与整理

2014 年在泉山林场进行数据采集，共设置临时标准地38 块，标准地面积为600 m2。调查林分起源、林龄、胸径、树高、郁闭度、枝下高等，其中起测胸径为5.0 cm，共测得200 组灯台树数据，342 组枫桦数据，220 组核桃楸数据以及黄波罗241 组数据，分别树种随机抽取其中75%的数据作为建模数据，其余25%数据作为检验数据，各树种调查因子统计见表1。

表1 各树种调查因子统计

2.2 最优模型的选择

通过查阅相关文献中有关的树高曲线模型，以常见的17个树高曲线对树高-胸径规律进行拟合，计算各模型的参数，并用R2、偏差（Bias）和均方根误差（RMSE）对模型精度进行检验，结果表明17 个常见的树高-胸径模型能较好地模拟树高与胸径的关系，故选取其作为辽宁省东部山区主要阔叶树种最优树高曲线。所以本文应用17 个常见的树高曲线模型，通过非线性最小二乘法来模拟这些主要树种（灯台树、枫桦、核桃楸、黄波罗）的树高与胸径的关系，模型的形式基本上来自于一些比较常用的树高曲线模型，分别属于幂函数、双曲线、Schumacher式、单分子式、Richards式、Logistic式等（表2）。

表2 树高曲线方程

本研究中，使用偏差（Bias）、均方根误差（RMSE）和调整后的决定系数（adj-R2）来选取上述树种的树高与胸径的最优模型。adj-R2的大小决定预测值与实际值相关的密切程度，adj-R2越接近1，表示相关的方程式参考价值越高；RMSE 和Bias 的值越接近0 而adj-R2的值越接近1，说明模型的精度高［9-10］。adj-R2较大、Bias 的绝对值及RMSE 较小的模型，说明拟合精度较高，树高曲线较合理，因此，本研究通过综合分析3 个评价指标，选定各个树种的最优树高曲线。其中，偏差（Bias）、均方根误差（RMSE）和调整后的决定系数（adj-R2）的计算公式如下。

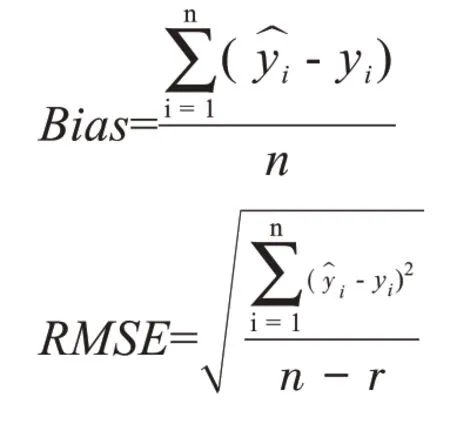
式中：yi为树高实测值；为预测值；n为样本数；r为模型参数个数［11］。

本研究基于阔叶树种的树高和胸径的实测数据，利用R软件［12］的nls模块实现的。

2.3 模型检验

模型的拟合优度不能完全反映模型的预测能力，为了评价模型的预测能力，模型检验必不可少。因此，本研究采用以下5个指标进行检验，调整后决定系数（adj-R2）、均方根误差（RMSE）、平均误差（ME）、平均绝对误差（MAE）、平均相对误差绝对值（MAE%），5个指标的具体定义见文献［12］。

其中:yi是观测值；yi是预测值；n是样本总数。

3 结果与分析

3.1 最优模型的选取

利用R 软件［13］的nls 模块，对17 个模型分别树种进行拟合，得出分别树种的各模型的误差分析，见表3。

综合分析评价因子，分别树种得到最优的树高模型。其中灯台树的最优模型是（14），枫桦的最优模型是（8），核桃楸的最优模型是（14），黄波罗的最优模型是（13）。

误 差 树 种 （1） （2） （3） （4） （5） （6）Bias RMSE R2误 差Bias RMSE R2误差Bias RMSE R2灯台树枫 桦核桃楸黄波罗灯台树枫 桦核桃楸黄波罗灯台树枫 桦核桃楸黄波罗树 种灯台树枫 桦核桃楸黄波罗灯台树枫 桦核桃楸黄波罗灯台树枫 桦核桃楸黄波罗树 种灯台树枫 桦核桃楸黄波罗灯台树枫 桦核桃楸黄波罗灯台树枫桦核桃楸黄波罗2.53E-03 6.12E-03 3.28E-03 2.19E-03 0.6340 0.8980 1.4672 0.6957 0.7132 0.7680 0.7550 0.7676（7）-1.68E-04-1.54E-03 1.71E-03 5.23E-04 0.5872 0.8789 1.4592 0.6883 0.7539 0.7777 0.7577 0.7725（13）-2.40E-04-4.96E-04 1.82E-03-6.05E-07 0.5951 0.8802 1.4689 0.6698 0.7473 0.7771 0.7545 0.7815 2.93E-03 8.40E-03 9.30E-03 3.28E-03 0.6449 0.9107 1.4722 0.7029 0.7032 0.7614 0.7534 0.7627（8）1.83E-03-5.58E-05 7.70E-03 7.33E-05 0.6035 0.8381 1.4644 0.6903 0.7401 0.7881 0.7560 0.7712（14）-3.66E-04-1.94E-03-9.31E-06 5.79E-04 0.3834 0.8797 1.4149 0.6870 0.7671 0.7774 0.7693 0.7734-3.90E-04-1.91E-03-6.42E-03-9.83E-04 0.5889 0.8890 1.5744 0.7064 0.7524 0.7726 0.7179 0.7604（9）-8.08E-04-3.20E-03 1.52E-03 1.51E-04 0.5985 0.8953 1.4509 0.6861 0.7444 0.7694 0.7604 0.7740（15）3.26E-03-1.16E-03 5.34E-03 3.40E-04 0.6143 0.8780 1.4628 0.6900 0.7057 0.7782 0.7565 0.7714 1.99E-02 3.14E-03-4.55E-02 2.16E-04 0.6548 0.8788 1.5076 0.6877 0.6940 0.7778 0.7413 0.7729（10）-1.41E-04-1.52E-03 2.41E-03 1.60E-04 0.3364 0.8868 1.4553 0.6874 0.7477 0.7737 0.7590 0.7731（16）1.45E-03-1.40E-03 4.55E-03 5.07E-04 0.7357 0.8784 1.4584 0.6893 0.7187 0.7780 0.7580 0.7718 4.28E-02 8.13E-03-5.14E-02 1.91E-03 0.7036 0.8822 1.4990 0.6868 0.6467 0.7761 0.7443 0.7735（11）-4.39E-04-1.52E-03 2.41E-03 1.60E-04 0.5962 0.8868 1.4553 0.6874 0.7463 0.7737 0.7590 0.7731（17）3.21E-03-1.26E-03 3.97E-03 3.44E-04 0.7547 0.8785 1.4610 0.6893 0.7301 0.7780 0.7571 0.7718 3.55E-02-3.11E-07-1.02E-07-3.21E-03 0.6012 0.8862 1.4842 0.7420 0.7015 0.7746 0.7493 0.7357（12）-1.05E-04-1.41E-03 2.41E-03 5.00E-04 0.5882 0.8787 1.4593 0.6886 0.7531 0.7779 0.7577 0.7723

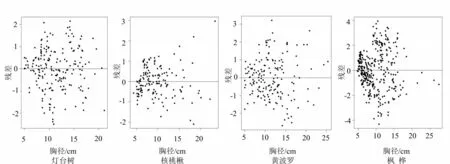
图1 不同树种最优树高曲线的残差图

残差分析如图1 所示，残差点在残差值为0 的线上下分布均匀，基本大多数都落在±2的标准残差之内，也有个别残差较大的样本，表明方程的拟合效果较好。通过以上分析和残差分布图的比较，以上各个树种的树高曲线模型的拟合效果都较好。

3.2 模型的检验

本研究用25%的数据进行模型预测能力的检验，采用以下3 个指标进行检验，调整后决定系数（adj-R2）、均方根误差（RMSE）、平均误差（ME），计算结果见表4。定系数在0.8 左右，均方根误差在0.4～1.5，模型误差也很小，说明经过筛选出的4 种树种的最优树高曲线拟合效果较好。

为了进一步检验模型的预测能力，对实测树高与模型拟合树高值进行T 检验（表5），结果显示实测值与拟合值无显著差异，筛选出的最优树高模型有较强的拟合预测能力。

表4 最优模型的拟合优度和检验结果

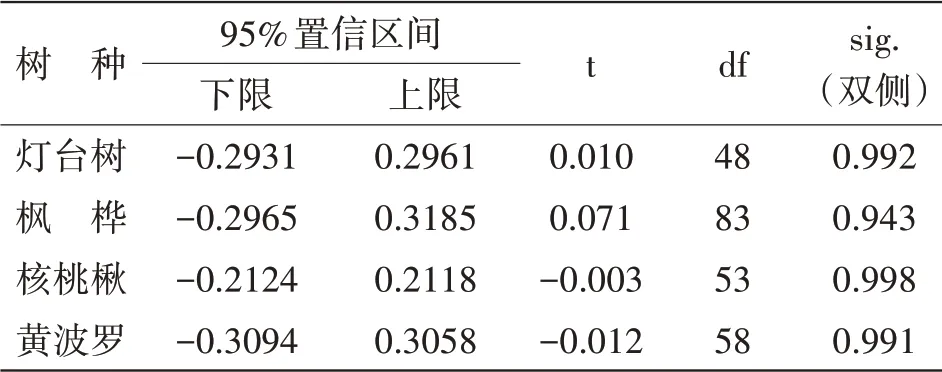
表5 实测树高与拟合树高值T检验结果

从表4 可以看出，4 种树种的树高曲线，调整决

统计分析建模数据，对各个树种的最优树高模型进行拟合，得到各个模型的方程参数，模型中各参数估计值见表6。

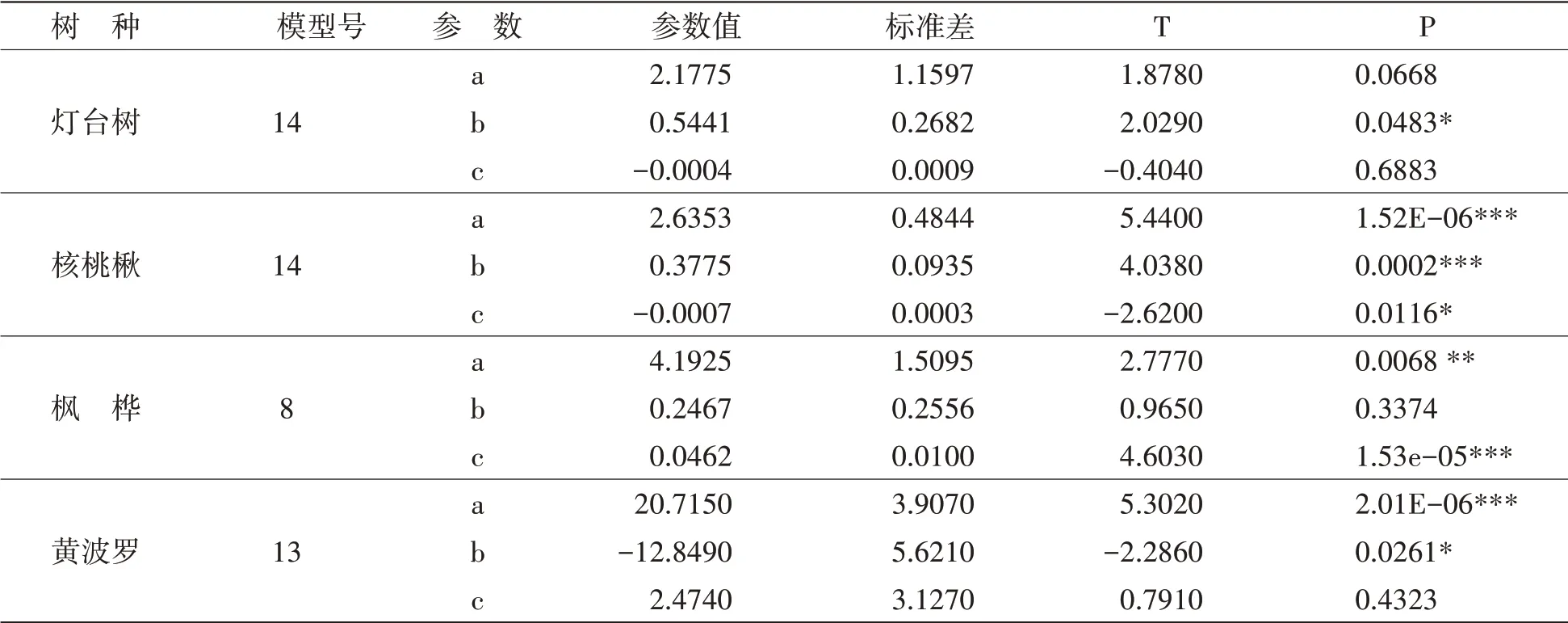
表6 模型中参数值

4 结论与讨论

本研究以17 个常见的树高-胸径模型来模拟宽甸泉山林场主要阔叶树种灯台树、枫桦、核桃楸和黄波罗的树高-胸径关系，从中为每个树种选取了最优模型，其中灯台树、核桃楸和黄波罗的最优模型是三参数模型，枫桦的最优模型为两参数模型。且每个树种的树高模型，误差较小，相关系数在0.78以上，方程的拟合效果较好。通过应用独立数据检验，各方程平均误差较小，因此，这些模型可以用来描述该树种树高的变化规律，通过测量胸径值，可以对该树种的树高进行预测。

本研究调查的数据数量有限，在以后的研究中，通过更多数据的采集提高方程的精度。本研究仅以胸径为自变量，还可以通过添加一些相关的林分变量构成标准树高曲线，增加模型更大的适用范围。本文所得模型可以为该地区主要阔叶树种提供树高曲线，可以用于相关的生长与收获预估模型。