FRM滤波器中应用积分梳状滤波器的研究
李杰,汪海涛
FRM滤波器中应用积分梳状滤波器的研究
李杰,汪海涛
(上海船舶电子设备研究所,上海 201108)
传统的频率响应屏蔽(Frequency Response Masking, FRM)滤波器由多个含有乘法器的滤波器构成,计算复杂度较高。提出了一种改进窄带低通FRM数字滤波器设计复杂度的方法,使用积分梳状滤波器作为屏蔽滤波器,以达到设计窄过渡带的滤波器的要求。仿真结果表明,在降低窄带低通FRM滤波器计算复杂度方面效果明显,有效地减少了乘法器的使用,降低了目标滤波器设计的阶数。该方法可以应用于窄过渡FRM数字滤波器的设计中。
频率响应屏蔽滤波器;积分梳状滤波器;计算复杂度;窄过渡带
0 引言
窄带低通滤波器是指通带和过渡带相对于采样频率都很窄的低通滤波器,对过渡带和通阻带纹波都有较高要求。由于过渡带的宽度与滤波器的阶数有关,过渡带变窄会增加滤波器的阶数即增加乘法器的个数[1-2]。如何在满足窄过渡带要求的前提下降低滤波器的阶数是研究的重点。现有的窄过渡带滤波器的设计方法主要有:预滤波器-均衡器技术,有限脉冲响应内插技术,并行结构技术,频率响应屏蔽(Frequency Response Masking, FRM)技术[3]。目前以FRM技术设计的窄过渡带滤波器应用较广,可设计任意带宽的滤波器,且对其的改进主要集中在结构和算法上。一般是对原型滤波器和屏蔽滤波器进行优化设计。
由于积分梳状滤波器的滤波计算中只有加法,没有乘法,只需将相邻的数据相加即可得到输出数据,不仅节省了硬件资源,同时大大减少了运算时间[4],因此本文将积分梳状滤波器用于FRM滤波器的屏蔽滤波器中,可以有效降低窄过渡带FRM滤波器的设计复杂度。
由于现有的水声对抗器材对低频窄带噪声的滤除有较高的要求,所以可以将基于积分梳状滤波器设计的FRM滤波器应用于这一领域。
1 频率响应屏蔽技术(FRM)
频率响应屏蔽(FRM)技术是设计窄过渡带滤波器最常用的方法,由于FRM技术可以产生任意带宽的滤波器,相对于传统的滤波器设计方法,该技术减少了乘法器的使用,进而降低了硬件资源的复杂度,所以近年来对其应用与研究较多[5-6],其基本结构如图1所示。
FRM滤波器的基本结构由原型滤波器,与原型滤波器幅度互补的互补滤波器以及两个屏蔽滤波器构成[4],通过进行内插得到过渡带较窄的滤波器,为内插因子,屏蔽滤波器的作用是去除原型滤波器内插引起的多余周期子带。原型滤波器及其互补滤波器以及两个屏蔽滤波器的传输函数为

图1 FRM滤波器的基本结构

其基本的传输函数为

其滤波过程原理如图2所示。图中和分别为滤波器的通带截止频率和阻带截止频率,为一个整数。图2(a)和图2(b)分别表示FRM滤波器的两种情况。图2(a)表示由插值后的原型滤波器提供过渡带的情况,图2(b)表示由插值后原型滤波器的互补滤波器提供过渡带的情况,两种方法产生的过渡带宽度相同。但是各个滤波器的通带宽度不同,而且每个滤波器中的子滤波器的阶数也不同,所以产生的目标滤波器的复杂度也不同。通过将以上参数代入不同的表达式来计算以上两种情况下的各个子滤波器的截止频率,使其达到最优,满足所设计的低复杂度滤波器的要求。
2 积分梳状滤波器
积分梳状(Cascade Integrator Comb, CIC)滤波器一般用来完成抗混叠(或去镜像)滤波,它的冲激响应函数为

式中:R为有限冲击响应(Finite Impulse Response, FIR)滤波器的长度或阶数。该滤波器是一个线性时不变系统,当通过卷积来计算输出信号时,可以看出其滤波计算只有加法而没有乘法,只需将相邻的数据相加即可得到输出数据,卷积公式为
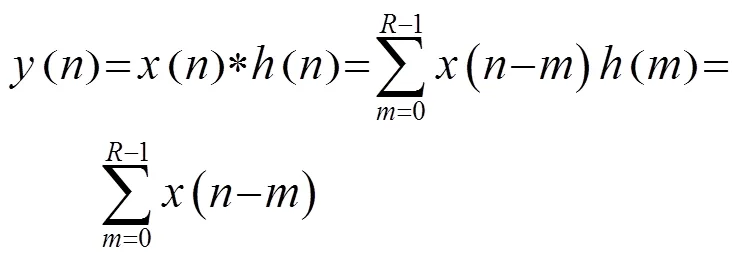
由此可以看出积分梳状滤波器不仅可以节省硬件资源,而且减少了运算时间。
由于FRM滤波器主要是通过减少乘法器的使用来的,所以研究方法主要集中在优化结构和优化算法上,可以将积分梳状滤波器(CIC)应用于FRM的结构优化设计中,将其作为屏蔽滤波器进行FRM滤波器的优化设计,去除内插后产生的多余镜像以及将有用频段过滤出来,同时减少了乘法器的使用,降低了设计复杂度[4]。但是由于CIC的幅频响应不够平坦,通带、过度带的分界不够明显,所以一般将其应用于低通FRM滤波器的设计中。当将其应用于带通滤波器的设计时,不能达到设计任意带宽滤波器的目的。
3 设计实例
本文中的FRM滤波器通过MATLAB软件来进行仿真设计,原型滤波器采用Remez算法来求解滤波器的系数,通过MATLAB中的Firpm函数来仿真实现,屏蔽滤波器采用一个5级的CIC滤波器(5级CIC级联阻带与通带的最小衰减为-67.32 dB),另一个也采用Firpm函数来仿真实现,选择合适的插值因子以及通带阻带纹波,通过观察各滤波器的阶数来进行比较。
本次设计为了方便观察过渡带的具体数值,频率没有进行归一化处理,选取的采样频率为40 kHz,原型滤波器的频率为5~6 kHz,过渡带为1 kHz,插值因子选择为10,过渡带变成了原来的1/10,只有100 Hz,通带波纹为0.01 dB,阻带纹波为65 dB,采用基本的一层FRM结构进行验证,仿真结果如图3所示。

图3中首先根据公式(1)以及给定的原型滤波器的数值设计出了其幅度互补的滤波器。然后对原型滤波器与互补滤波器进行插值来产生所要求的过渡带宽度,插值后的滤波器具有了周期性,其截止频率与采样频率和插值因子的值有关,之后根据原型滤波器和互补滤波器的频率特性,设计相应的屏蔽滤波器。本文为了说明将CIC滤波器应用于FRM滤波器时可以产生的效果,只将其中一个屏蔽滤波器用CIC滤波器替换,另一个屏蔽滤波器依然采用传统的设计方法,最后将以上各个子滤波器代入FRM滤波器的基本结构中,经过不同的滤波运算,产生所要求的滤波器。
为了与传统FRM滤波器的设计方法相比较,本文也采用传统方法设计(即屏蔽滤波器都采用传统的Remez算法进行设计)与上述性能要求一样的滤波器,其设计仿真结果如图4所示。
由图3和图4可知,两种方法设计的窄带低通滤波器的性能相同,但是由于CIC滤波器没有用到乘法器,只有原型滤波器和另一个屏蔽滤波器的设计中用到了乘法器,减少了乘法器的数量,根据MATLAB计算的结果可知,上述实例中采用CIC设计的滤波器所需要的阶数为275,传统设计方法所使用的阶数为324,减少了49阶,滤波器的阶数决定乘法运算的次数,也即乘法器数量减少了49,比传统方法降低了15%的复杂度。由于在现场可编程门阵列(Field Programmable Gate Array, FPGA)硬件资源中乘法的实现相对较复杂[7],所以减少乘法器的使用可以降低硬件的复杂度和硬件的规模,进而提高运算速度。
为了进一步对所设计的滤波器的性能进行说明,本文采用最优的切比雪夫逼近法设计具有相同性能的FIR滤波器,通过使用MATLAB中的滤波器设计分析(Filter Design Analysis Tool, FDATool)工具箱直接设计实现,其所需的阶数为1 434。滤波器的设计结果如图5所示。
将本文所提出方法与通过使用切比雪夫逼近法直接设计的FIR滤波器和传统FRM技术设计的滤波器进行对比,可以看到相对于切比雪夫逼近法直接设计,滤波器的阶数减少了80.8%,相对于传统的FRM设计方法,滤波器的阶数减少了15%,在滤波器性能相同的情况下,所需要的阶数减少了很多。
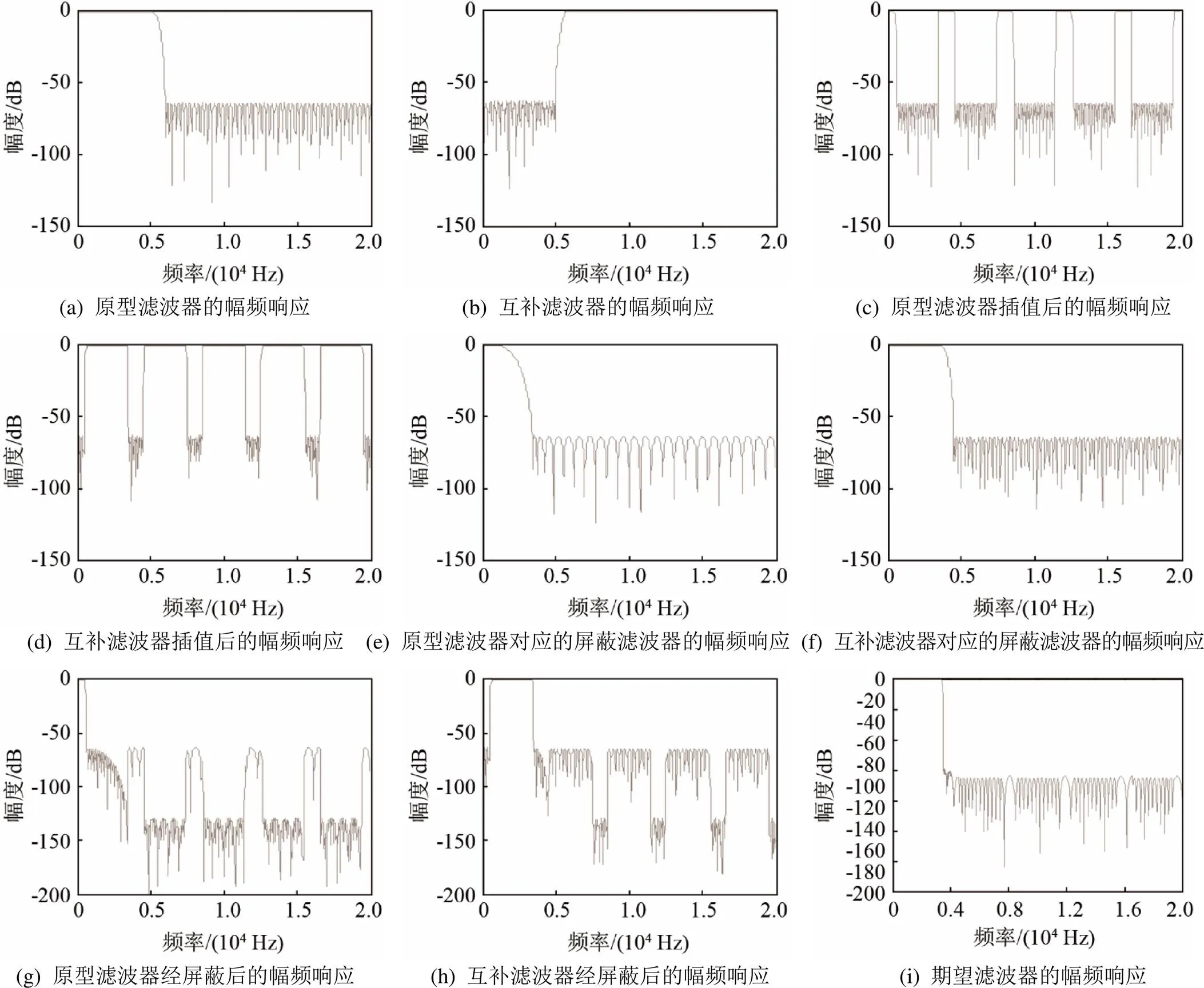
图4 传统设计方法的MATLAB仿真结果
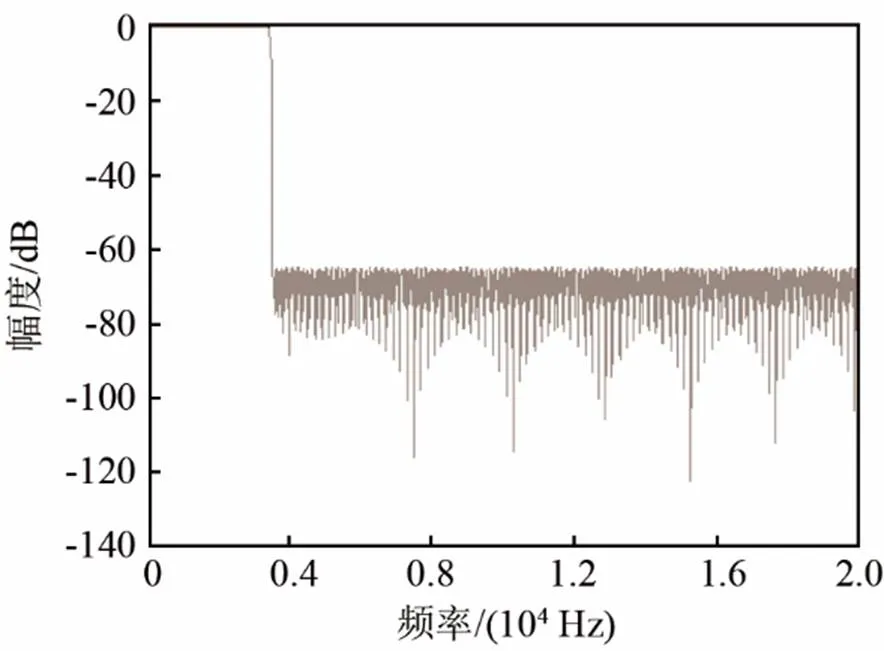
图5 FDAT工具箱设计的低通滤波器
以上是对使用CIC进行低通FRM滤波器设计的仿真验证,使用多个FRM低通滤波器可以得到相应的带通FRM滤波器。但是由于CIC的特点,当直接使用CIC进行FRM带通滤波器设计,并将其作为屏蔽滤波器时,达不到截取有用频带的目的,截取出来的幅频响应与另一支路的幅频响应进行相加以后得到的带通滤波器不具有期望的通带特性,不能满足在期望通、阻带截止频率要求下的带宽,不满足设计指标要求。
本文选取的采样频率为40 kHz,设计一个过渡带为125 Hz,带宽为2.25 kHz的滤波器,插值因子为8,通带波纹为0.01 dB,阻带纹波为65 dB。采用基本的一层结构进行设计,其仿真结果如图6所示,表明设计不满足指标要求。

图6 CIC用于FRM带通滤波器设计的模拟结果
4 结论
根据以上的仿真结果可以看出,将CIC滤波器用于FRM窄带低通滤波器的设计中,可以有效地减少滤波器的乘法器数量,降低阶数,进而降低了对所需硬件资源的要求。结合水声工程领域中的应用,以及水声领域频率的特点,可以将其应用于去除窄带低频干扰噪声。但是由于积分梳状滤波器的特点,当选取不同的采样频率和不同的插值(或抽取)因子以及延迟因子时,其所能产生的通带带宽范围会有区别,所以其所能滤除的频率的带宽范围有限,一般将其应用于低频信号处理。
本文的创新点在于将积分梳状滤波器用于FRM结构中。通过实例分析可知,将CIC应用于FRM滤波器可以降低设计所使用的乘法器的数量,从而降低了设计的复杂度,在用FPGA硬件实现时,减少了硬件规模,进而提高了运算速度。
[1] 王欣. 离散信号的滤波[M]. 北京: 电子工业出版社, 2001.
WANG Xin. Filtering of discretesignals[M]. Beijing: Electronic Industry Press, 2001.
[2] 胡广书. 数字信号处理―理论、算法与实现[M]. 2版. 北京: 清华大学出版社, 1998.
HU Guangshu. Digital signal processing-Theory、algorithm and implementation[M]. 2nd. Beijing: Tsinghua University Press, 1988.
[3] 傅乔. FRM滤波器及二维滤波器的优化设计研究[D]. 长沙: 长沙理工大学, 2009.
FU Qiao. Optimal design of FRM filters and two-dimensional filters[D]. Changsha: Changsha University of Science and Technology, 2009.
[4] 陈蕾, 姚远程. 基于System Generator 的数字下变频设计[J]. 电子设计工程, 2012, 20(24): 74-78.
CHEN Lei, YAO Yuancheng. Design of digital down-conversion based on the system generator[J]. Electronic Design Engineering, 2012, 20(24): 74-78.
[5] SINHA T, BHAUMIK J. Designing of sharp transition low pass FIR filter using multistage FRM approach[C]//DevIC, Kalyani, India, 2017, 23-24.
[6] WEI Y, LIU D B. Improved design of frequency-response masking filters using band-edge shaping filter with non-periodical frequency response[J]. IEEE Transactions on Signal Processing, 2013, 61(13): 3269-3278.
[7] LI S G, ZHANG J. Efficient FPGA implementation of sharp FIR filters using the FRM technique[J]. IEICE Electronics Express, 2009, 23(6): 1656-1662.
The study of FRM filter using cascade integrator comb filter
LI Jie, WANG Haitao
(Shanghai Marine Electronic Equipment Research Institute, Shanghai 201108, China)
The traditional frequency response masking (FRM) filter consists of multiple filters with multiplier unit, which has a relatively high computational complexity. In this paper a method of improving the design complexity of narrow-band low pass FRM digital filter is proposed, in which the cascade integrator comb (CIC) filter is used as the masking filters to satisfy the design requirements of narrow transition band and to lower the computational complexity filter. The results of simulation show that this method is quite effective in reducing the computational complexity of narrow-band low pass FRM filter and in reducing the use of the multiplier units and the order of the target filter. Therefore, this method can be used in the design of narrow transition band FRM digital filter.
frequency response masking(FRM) filter; cascade integrator comb(CIC) filter; computational complexity; narrow transition band
TN713+.7
A
1000-3630(2020)-02-0251-06
10.16300/j.cnki.1000-3630.2020.02.021
2018-12-24;
2019-03-24
李杰(1991-), 男, 山西大同人, 硕士, 研究方向为水声对抗技术。
李杰, E-mail:ichbinjack@126.com

