基于声学脉冲响应的室内建图算法研究

覃虹菱，王玫,2，宋浠瑜，周陬，罗丽燕

基于声学脉冲响应的室内建图算法研究

覃虹菱1，王玫1,2，宋浠瑜1，周陬1，罗丽燕1

(1. 桂林电子科技大学认知无线电与信息处理省部共建教育部重点实验室，广西桂林 541004；2.桂林理工大学信息科学与工程学院，广西桂林 541004)

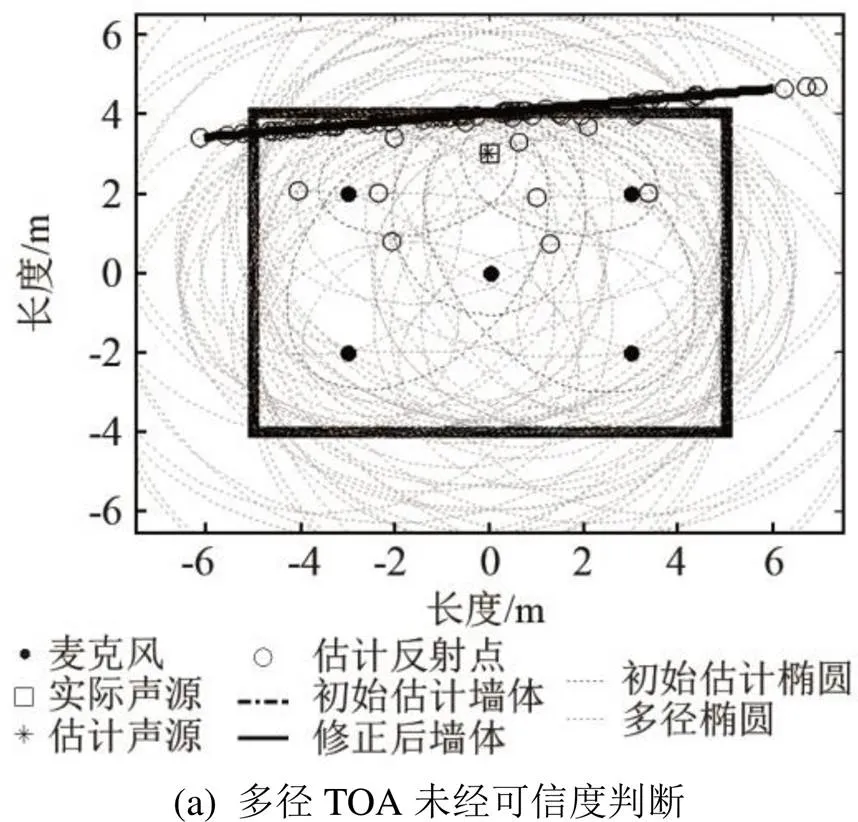
由于室内环境下噪声及混响干扰造成声学脉冲响应(Acoustic Impulse Response, AIR)的波达时间(Time of Arrival, TOA)模糊，导致现有室内空间几何建图技术存在计算复杂等缺点，提出一种基于AIR可信度判断与霍夫变换结合的定位和建图一步完成的方法。该方法基于到达时间差(Time Difference of Arrival, TDOA)迭代估计声源位置并计算准确的TOA，随后基于声收发设备与一阶反射TOA关于反射面的椭圆约束关系，结合可信度判断与霍夫变换，筛选可信低阶TOA以实现室内反射面的二维位置估计。蒙特卡洛仿真结果表明，在混响时间60为0.134 7 s、AIR误差标准差为22.7×10-3ms、大小为10 m×8 m×4 m复杂室内环境下，墙面定位平均距离误差为10.1 cm，平均角度误差为2.795 8°。在大小为5.26 m×3.5 m×3.35 m的真实房间中，该方法可以实现声源与墙体位置的同时定位，完成规则盒型房间的二维地图重构，且墙面定位平均距离误差为2.6 cm，平均角度误差为2.17°。

声学脉冲响应；室内定位与建图；椭圆约束；霍夫变换

0 引言

随着基于用户位置信息的相关技术的应用和发展，位置服务已经成为人们日常工作、生活所必须的一项基本服务需求，常用于室内定位、机器人导航等[1-2]。这种技术应用时需要一个环境地图。传统的室内建图方法，如基于视觉图像[3]、测距传感[4]的移动机器人即时定位与地图构建(Simultaneous Localization and Mapping, SLAM)等都因为其特定的条件依赖，未能得到推广。在室内环境中，声信号的传播在一定程度上反映了室内布置和结构信息，且相比电磁波、光波拥有更低的波速，更适用于室内地图的创建[5]。

房间结构的混响特性会使得声学脉冲响应(Acoustic Impulse Response, AIR)中波达时间(Time of Arrival, TOA)存在高阶反射早于低阶反射的情况，造成TOA模糊问题。文献[6]、[7]采用近墙单发单收方式避免TOA产生模糊，但是完成多个反射面的估计需要单声源移动测量多次，此位移过程中的累积位姿误差降低了其定位与重构性能。相对于单麦克风，麦克风阵列在时域和频域的基础上增加了空间域，对声音信息的处理能力增强[8]。文献[9]通过欧式距离阵(Euclidean Distance Matrix, EDM)将AIR中的一阶反射TOA分配到各个墙体来解决TOA模糊，再基于声源、虚声源与反射面的几何位置关系完成反射面估计，测量步骤简单但后续计算繁琐。基于收发设备与反射面之间的椭圆约束位置几何关系也可以直接定位反射面位置。文献[10]、[11]分别通过到达方向(Direction of Arrival, DOA)和近墙先验条件的方式解决TOA模糊问题。但前者仅适用于单反射面估计，后者虽运用霍夫变换进行降噪处理，但其采用的非迭代到达时间差(Time Difference of Arrival, TDOA)声源定位算法与集中型麦克风阵型的组合方式在低信噪比环境下定位精度较低，并传递到后续的反射面估计。文献[12]以任意排布麦克风阵列方式布置大量锚节点，结合地图映射的尺度变换(Multi-dimensional Scaling with Map Matching, MDS-MAP)、EDM和霍夫变换提出一种多路径辅助协同定位和映射(Multipath-aided Cooperative Localization and Mapping, MCLAM)算法来处理每组节点的数据，实现复杂且计算量大。

本文充分考虑了麦克风阵元分布对声源位置估计精度的影响，针对现有空间几何重构方案中声源定位方法的缺点，利用基于TDOA最小二乘思想的列文伯格-马夸尔特算法(Levenberg-Marquardt Algorithm, LMA)[13]对声源位置进行估计，并由此得到准确的TOA信息；再利用一阶反射TOA建立声收发设备与反射墙面之间的椭圆约束条件，通过公切线算法(COmmon Tangent Algorithm, COTA)[14]对反射面进行初步估计；最后加入不同声源位置的AIR，并利用可信度判断找到混响环境中的可信低阶多径TOA，通过霍夫变换降低噪声影响，获得更为准确的墙面位置估计的修正结果。

1 系统模型

1.1 椭圆约束几何关系

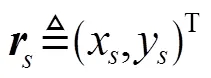
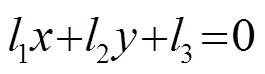
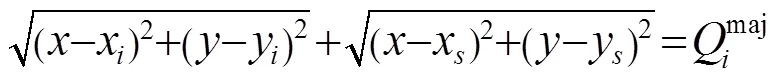
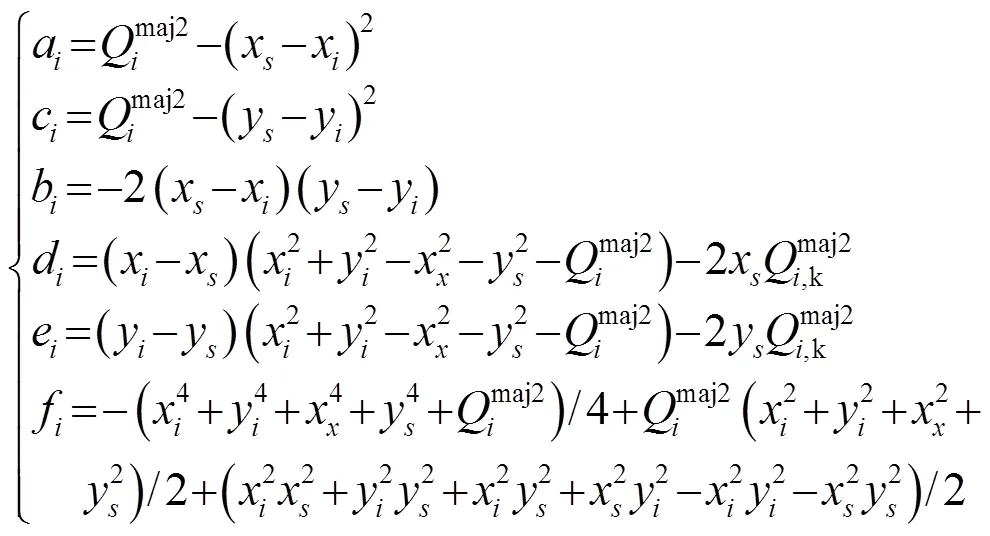
根据投影几何理论，图1描述的椭圆几何约束关系可以表示为

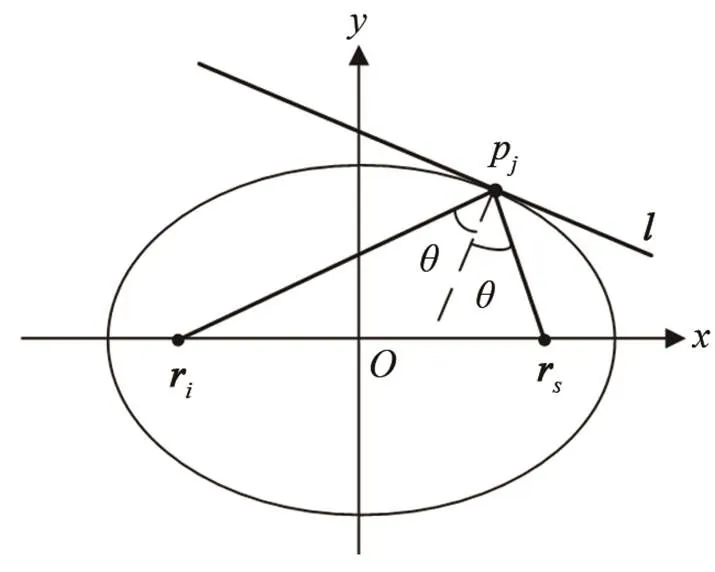
图1 声收发设备及反射面关于一阶反射的椭圆几何关系

1.2 系统框图

即时定位与地图构建系统框图如图2所示。本文工作涉及到图2中虚框所示的两个部分，其中，表示不同声源位置，表示房间中的不同反射面。

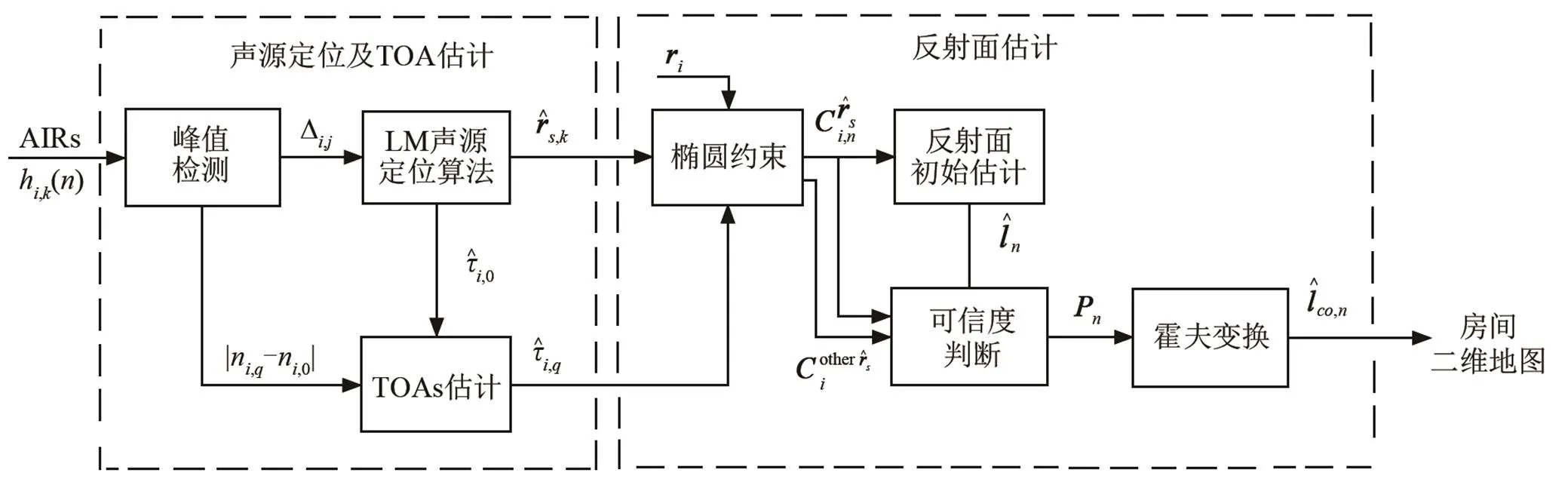
图2 即时定位与地图构建系统框图

2 声源定位及TOA估计

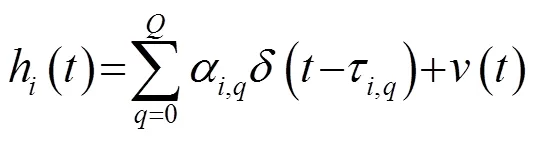
由于设备之间存在异步问题，利用TDOA迭代定位算法可得到声源位置，再求出AIR中一系列反映各阶反射的准确TOA。对于基于TDOA的声源定位，声源在阵列内部时，定位精度比远离阵列时的定位精度高[15]。采取分布式麦克风阵列的阵型，能够增大麦克风阵列的相对基线长度，提高声源定位的精度，同时也能够使反射点的分布更加分散，对反射面的位置估计不易产生角度误差。

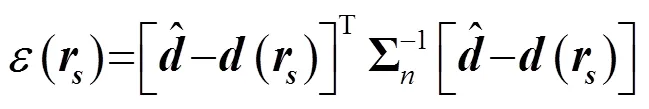
声源位置的迭代更新公式为

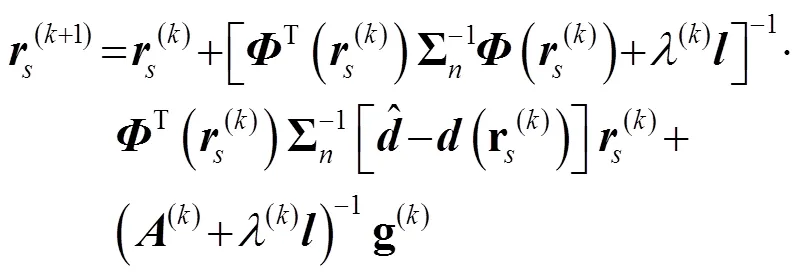
3 反射面估计

3.1 反射面初始估计

多接收情况下，单个源与接收点之间会形成一组关于同一反射面的椭圆约束，这组椭圆的公切线则对应于反射面的位置。于是由式(4)有

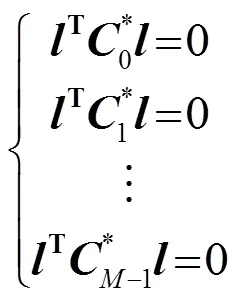
3.2 可信度判断与霍夫变换结合的修正估计

由于AIR中的TOA信息受噪声和混响干扰，式(9)得到的结果不能保证对应于真实的反射面。充分利用声传播的多径TOA信息，并采用可信度判断与霍夫变换结合的方式，可避免TOA模糊问题的复杂求解，提高反射面估计的鲁棒性。具体步骤如下：(1) 通过在声场中不同位置放置声源，得到更多数据来源。(2) 将声源靠近反射面，以保证AIR中直达之后的第一个脉冲即为来自该反射面的一阶反射，用于3.1节中的初始估计；(3) 选取AIR中除直达外的多径TOA，通过可信度判断剔除与指定反射面无关的TOA项，得到可信反射点集合，再利用霍夫变换的点线转换特性得到修正后更接近真实反射面的位置估计。

3.2.1 可信度分析

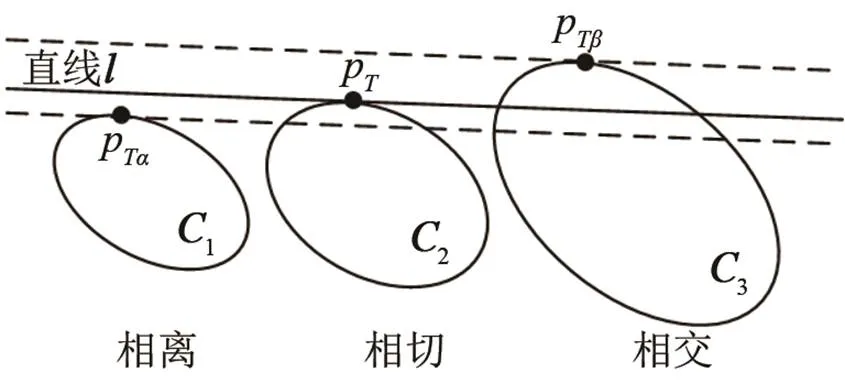
图3 直线椭圆位置关系与反射点选取

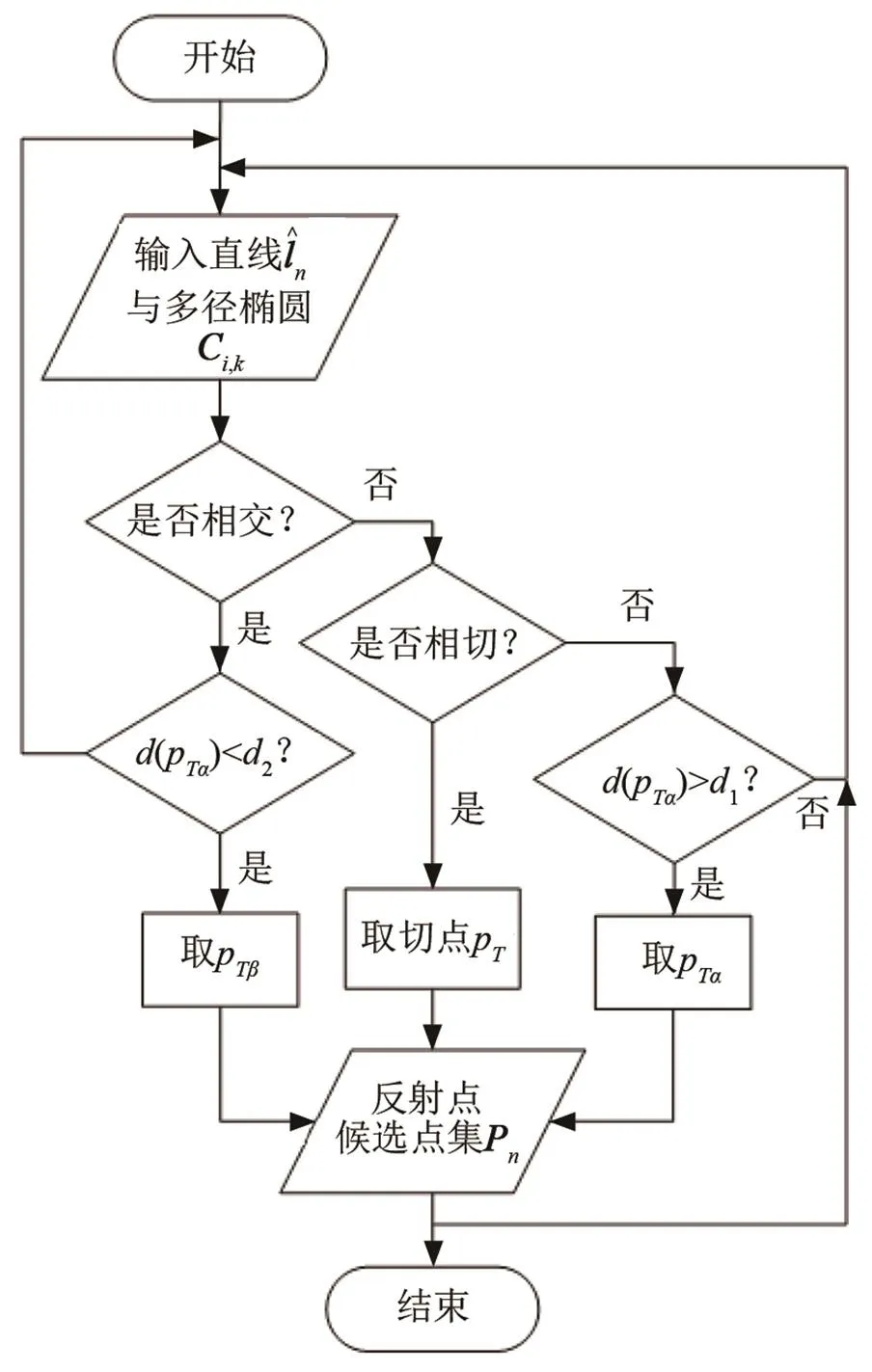
图4 反射点候选点集选取流程图

3.2.2 霍夫变换

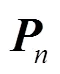
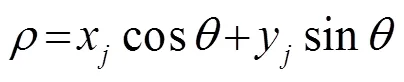
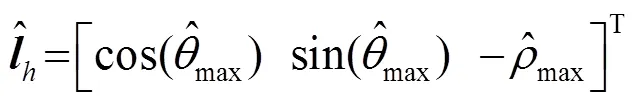
4 实验

4.1 数值仿真实验

不同噪声标准差情况下声源的平均定位误差如表1所示。

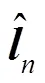
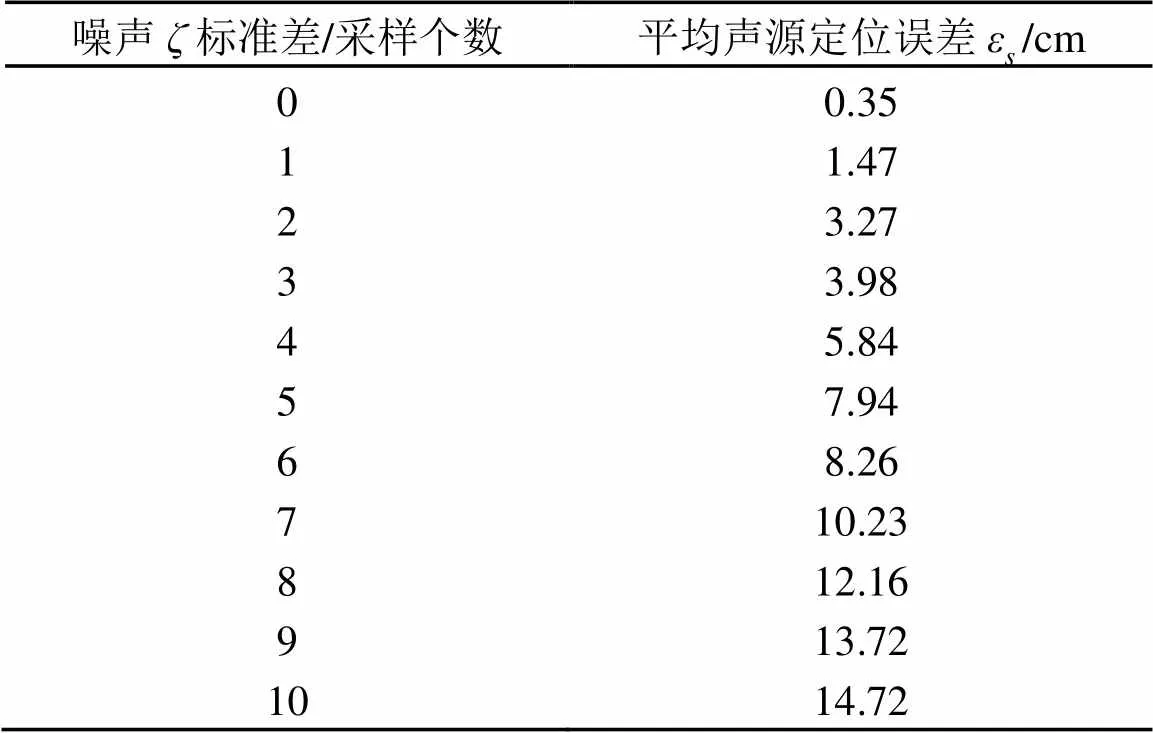
表1 声源定位平均误差

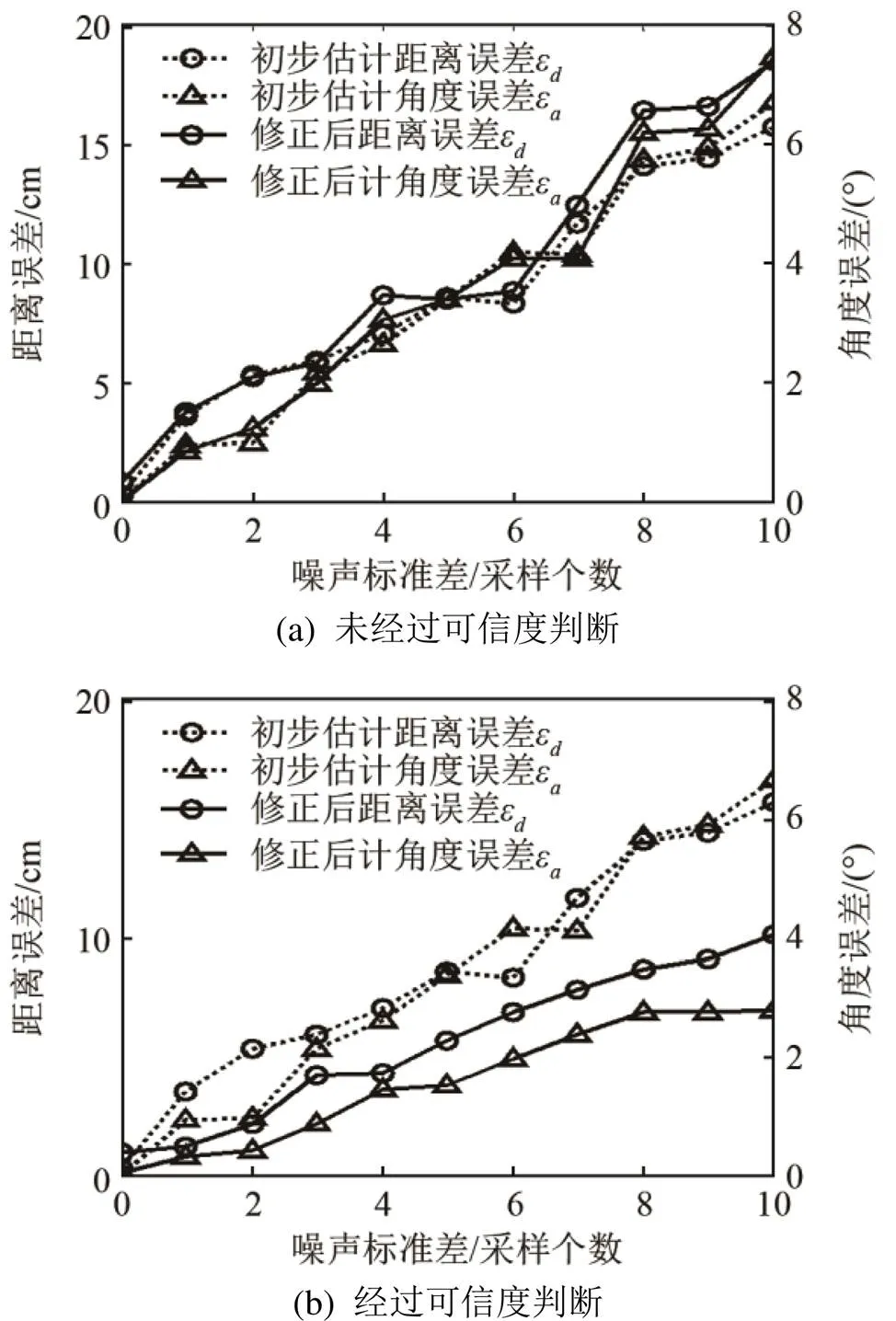
图7 初始估计与加入3个多径TOA后的修正性能对比

4.2 真实场景实验

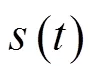
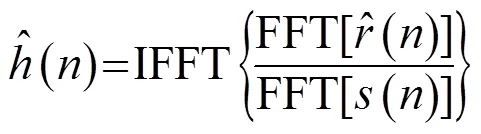
实际环境中的AIR多为锯齿波形，因此对其包络进行峰值检测，其他参数设置参照4.1节。

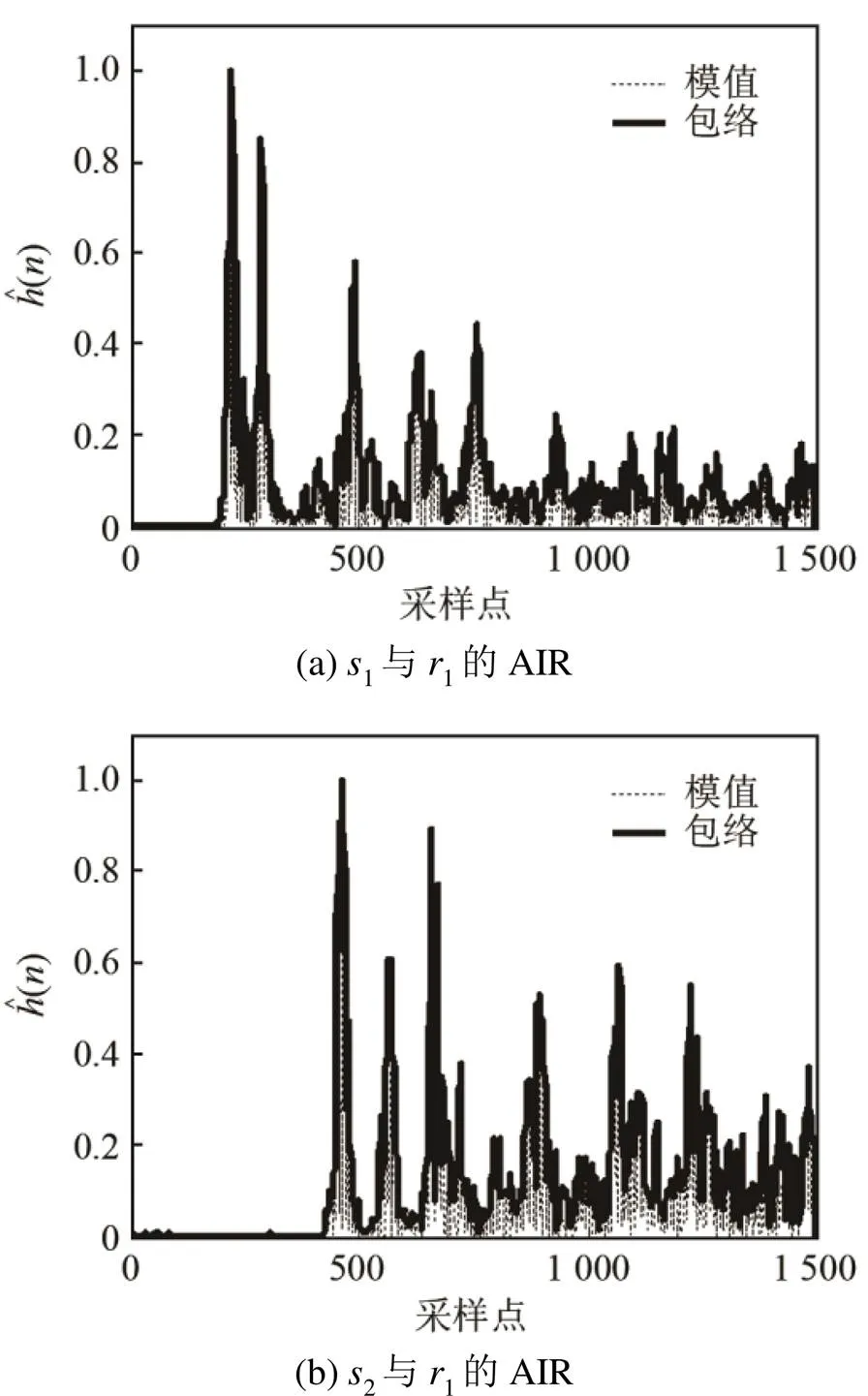
图8 真实环境中不同收发位置的声学脉冲响应

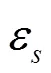
表2 真实环境声源定位误差

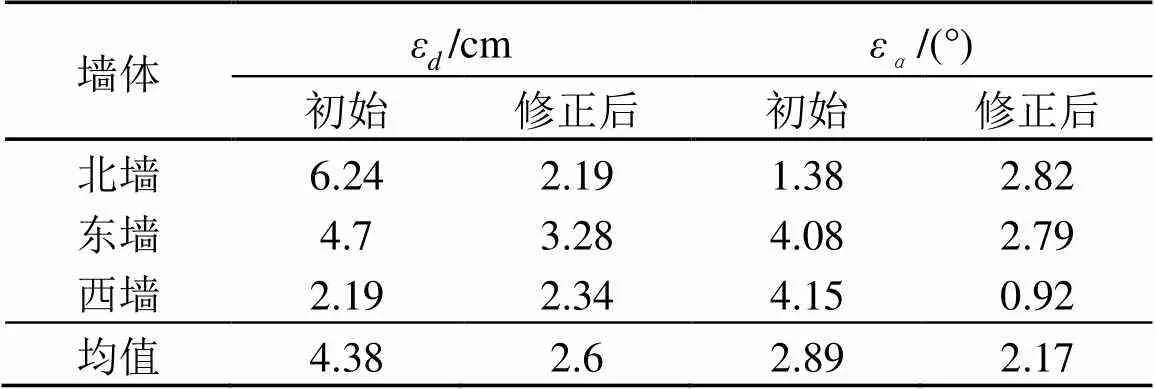
表3 真实环境墙体估计误差

5 结论

针对现有室内建图技术存在的高成本、高计算复杂度等缺点，本文提出了一种基于AIR的定位与建图一步完成的方法。该方法首先在异步情况下通过声源定位得到准确的TOA；再根据椭圆几何约束关系，通过COTA算法对反射面进行初始估计；最后通过可信度判断与霍夫变换结合的方式筛选多径TOA，对初始估计进行修正。蒙特卡洛模拟实验和真实房间实验表明，该方法能够在存在噪声及混响的室内环境中重构房间二维几何地图，且通过可信度判断与霍夫变换结合的方式提升了算法的鲁棒性。

原始的霍夫变换需要大量的候选点集支撑，但大量选取多径TOA也加大了计算量。下一步将对霍夫变换算法进行改进，加强其在少量数据情况下的抗噪能力；或是选择并改进筛选可信低阶TOA的方法，使其更加高效。

[1] KOLODZIEJ K W, HJELM J. Local positioning systems: LBS applications and services[M]//Local Positioning System, LBS Applications and Services, 2006: 101-158.

[2] 赵锐, 钟榜, 朱祖礼, 等. 室内定位技术及应用综述[J]. 电子科技, 2014, 27(3): 154.

ZHAO Rui, ZHONG Bang, ZHU Zuli, et al. Overview of indoor positioning technology and application[J]. Electronic Science & Technology, 2014, 27(3): 154.

[3] FUENTES-PACHECO J, RUIZ-ASCENCIO J, RENDÓN- MANCHA J M. Visual simultaneous localization and mapping: a survey[J]. Artificial Intelligence Review, 2015, 43(1): 55-81.

[4] 刘建华, 刘华平, 杨建国, 等. 测距式传感器同时定位与地图创建综述[J]. 智能系统学报, 2015, 10(5): 655-662.

LIU Jianhua, LIU Huaping, YANG Jianguo, et al. Overview of simultaneous location and map creation of ranging sensors[J]. Journal of Intelligent Systems, 2015, 10(5): 655-662.

[5] 吴硕贤, 赵越喆. 室内声学与环境声学[M]. 广州: 广东科技出版社, 2003.

WU Shuoxian, ZHAO Yuezhe. Room acoustics and environmental acoustics[M]. Guangzhou: Guangdong Science & Technology Press, 2003.

[6] MOORE A H, BROOKES M, NAYLOR P A. Room geometry estimation from a single channel acoustic impulse response[C]// Signal Processing Conference. IEEE, 2014: 1-5.

[7] MARKOVICA D, ANTONACCI F, SARTI A, et al. Estimation of room dimensions from a single impulse response[C]//Applications of Signal Processing To Audio and Acoustics, IEEE, 2014: 1-4.

[8] 石婷. 麦克风阵列声源定位算法研究综述[J]. 科技视界, 2016(27): 274-274.

SHI Ting. Review of research on microphone array sound source localization algorithm[J]. Science and Technology Vision, 2016(27): 274-274.

[9] DOKMANIĆ I, DAUDET L, VETTERLI M. From acoustic room reconstruction to slam[C]//IEEE International Conference on Acoustics, Speech and Signal Processing, IEEE, 2016: 6345-6349.

[10] REMAGGI L, JACKSON P J B, COLEMAN P, et al. Room boundary estimation from acoustic room impulse responses[C]//Sensor Signal Processing for Defence, IEEE, 2014: 1-5.

[11] ANTONACCI F, FILOS J, THOMAS M R P, et al. Inference of Room Geometry From Acoustic Impulse Responses[J]. IEEE Transactions on Audio Speech & Language Processing, 2012, 20(10): 2683-2695.

[12] NASERI H, KOIVUNEN V. Cooperative simultaneous localization and mapping by exploiting multipath propagation[J]. IEEE Transactions on Signal Processing, 2016, 65(1): 200-211.

[13] MENSING C, PLASS S. Positioning algorithms for cellular networks using TDOA[C]//IEEE International Conference on Acoustics Speech and Signal Processing Proceedings. IEEE, 2006: IV-IV.

[14] FILOS J, CANCLINI A, THOMAS M R P, et al. Robust inference of room geometry from acoustic measurements using the hough transform[C]//Signal Processing Conference, 2011, European. IEEE, 2010: 161-165.

[15] 金博楠, 徐晓苏, 张涛, 等. 基于TDOA定位的阵列布放结构研究[J]. 导航定位与授时, 2017, 4(6): 29-36.

JIN Bonan, XU Xiaosu, ZHANG Tao, et al. Research on array placement structure based on TDOA positioning[J]. Navigation and Timing, 2017, 4(6): 29-36.

[16] 覃虹菱. 基于声学脉冲响应的麦克风阵列室内几何重构关键技术研究[D]. 桂林: 桂林电子科技大学, 2019.

[17] DUDA R O, HART P E. Use of the Hough transformation to detect lines and curves in pictures[J]. Cacm, 1972, 15(1): 11-15.

[18] ALLEN J B, BERKLEY D A. Image method for efficiently simulating small‐room acoustics[J]. J. Acoust. Soc. Am., 2016, 65(S1): 943-950.

[19] FARINA A. Simultaneous measurement of impulse response and distortion with a swept-sine technique[J]. Proc. Conv. Audio Eng. Soc. Paris, 2000, 24: 18-22.

Research on indoor mapping algorithm based on acoustic impulse response

QIN Hongling1, WANG Mei1,2, SONG Xiyu1, ZHOU Zou1, LUO Liyan1

(1. Provincial Ministry of Education Key Laboratory of Cognitive Radio and Signal Processing, Guilin University of Electronic Technology, Guilin 541004, Guangxi, China; 2. School of Information Science and Engineering, Guilin University of Technology, Guilin 541004, Guangxi, China)

The existing indoor mapping technology has the shortcomings in high cost and high computational complexity, which is caused by the TOA (time of arrival) ambiguity of the acoustic impulse response (AIR) due to noise and reverberation in the indoor environment. To solve this problem, an indoor localization and mapping method based on combining AIR credibility judgment and Hough transform is proposed in this paper. Firstly, the method iteratively estimates the position of the sound source based on the Time Difference of Arrival (TDOA) and calculates the accurate TOA. Then, by using the elliptical constraint relationship between the acoustic transceiver and the first-order reflection TOA on the reflective surface and combining the credibility judgment and Hough Transform, the reliable low-order TOA is selected to achieve the two-dimensional position estimation of the indoor reflective surface. Monte Carlo simulation results show that in the complex indoor environment of 10m×8m×4m with reverberation time60of 0.134 7 s and AIR error standard deviation of 22.7×10-3ms, the average distance error of wall localization is 10.1cm, and the average angular error is 2.795 8°. In the following experiments in a real room of 5.26 m×3.5 m×3.35 m, this method can realize the simultaneous localization of sound source and wall position, and complete the two-dimensional reconstruction of a box-type room. And the average distance error of wall localization is 2.6 cm, and the average angular error is 2.17°.

acoustic impulse response (AIR); indoor localization and mapping; elliptic constraint; Hough transform

TU112

A

1000-3630(2020)-02-0243-08

10.16300/j.cnki.1000-3630.2020.02.020

2018-11-03;

2018-12-29

国家自然科学基金 (61771151)、广西重点研发计划项目(AB17292058)、广西自然科学基金(2016GXNSFBA38014)、中国博士后科学基金(2016M602921XB)、广西高校无人机遥测重点实验室开放基金(WRJ2016KF01)资助项目

覃虹菱(1994－), 女, 四川成都人, 硕士研究生, 研究方向为室内定位与建图。

宋浠瑜,E-mail: songxiyu@guet.edu.cn