基于神经网络和遗传算法的锭子弹性管性能优化
莫 帅, 冯战勇, 唐文杰, 党合玉, 邹振兴
(1. 天津工业大学 机械工程学院, 天津 300387; 2. 天津工业大学 天津市现代 机电装备技术重点实验室, 天津 300387)
减振弹性管作为纺织锭子的关键精密部件,与轴承座和多层吸振卷簧等精密零件相互配合,共同组成了锭子下弹性阻尼锭胆系统。常用类型的精密锭子结构中,减振弹性管因上端与轴承座内孔紧密配合而形成了竖直的悬臂梁结构,配合其特殊的稀疏螺旋槽结构,显著增加了弹性管轴径向的弹性,达到对锭子旋转体高速下自动定心、降低振动、吸收噪音的目的,提高纺纱质量和效率[1]。
目前,全球的纺织制造业发展良好,但针对纺织机械的基础研究较为薄弱,锭子中减振弹性管是其不可或缺的关键零部件,国内外对其研究较少。吴文英等[2]推导了开螺旋槽弹性管的等效抗弯刚度和底部刚度系数的计算公式,分析了弹性管各参数对其刚度及振动性能的影响;王志勇等[3]从理论和实验数据二方面分析讨论了弹性管材料及结构参数对其弹性的影响,同时讨论了加工工艺对弹性管弹性的影响;彭来深等[4]通过对弹性管加工工序、装夹方式、夹具及刀具进行改进,提高了弹性管锭底孔相对外圆的同轴度,有效降低了锭子高速运转时的振程。由于开螺旋槽部分的结构参数对弹性管整体性能影响很大,而锭子作为精密机械专件,结构的微小变化都会有效提升锭子性能,因此,有必要对减振弹性管的工艺参数进行优化设计,以达到实际工况下的最优性能。
本文将弹性管螺旋槽结构以矩形弹簧近似分析,构建了螺旋槽部分的抗弯刚度及减振弹性管底部振幅的数学模型,并以弹性管性能的主要影响参数槽宽、螺距、壁厚、材料弹性模量为设计变量,结合径向基神经网络和遗传算法对其刚度和底部振幅进行多目标优化设计,实现高速下锭子的稳定性提升。
1 弹性管力学性能分析
将常用锭子减振弹性管的螺旋槽部分按矩形截面圆柱弹簧近似处理,如图1所示。
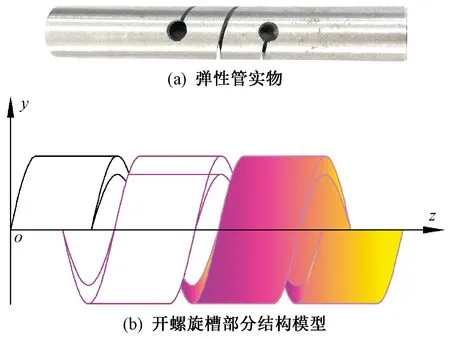
图1 弹性管实物及螺旋槽分析模型Fig.1 Elastic tube physical (a) and spiral groove analysis model (b)
已知减振弹性管抗弯刚度Jeq为
式中:α为弹簧的螺旋角,(°);Bn、Bb分别为弹簧丝截面对主法线和次法线的弯曲刚度,N/m;C为弹簧丝截面对切线的扭转刚度,N/m。
由于弹性管内部会受到锭杆高速旋转引起的激振力,造成锭底的摩擦磨损及锭子运行的振动加剧,因此,锭底处(即弹性管底部)振动性能的控制十分重要。图2示出弹性管底部变形示意图。
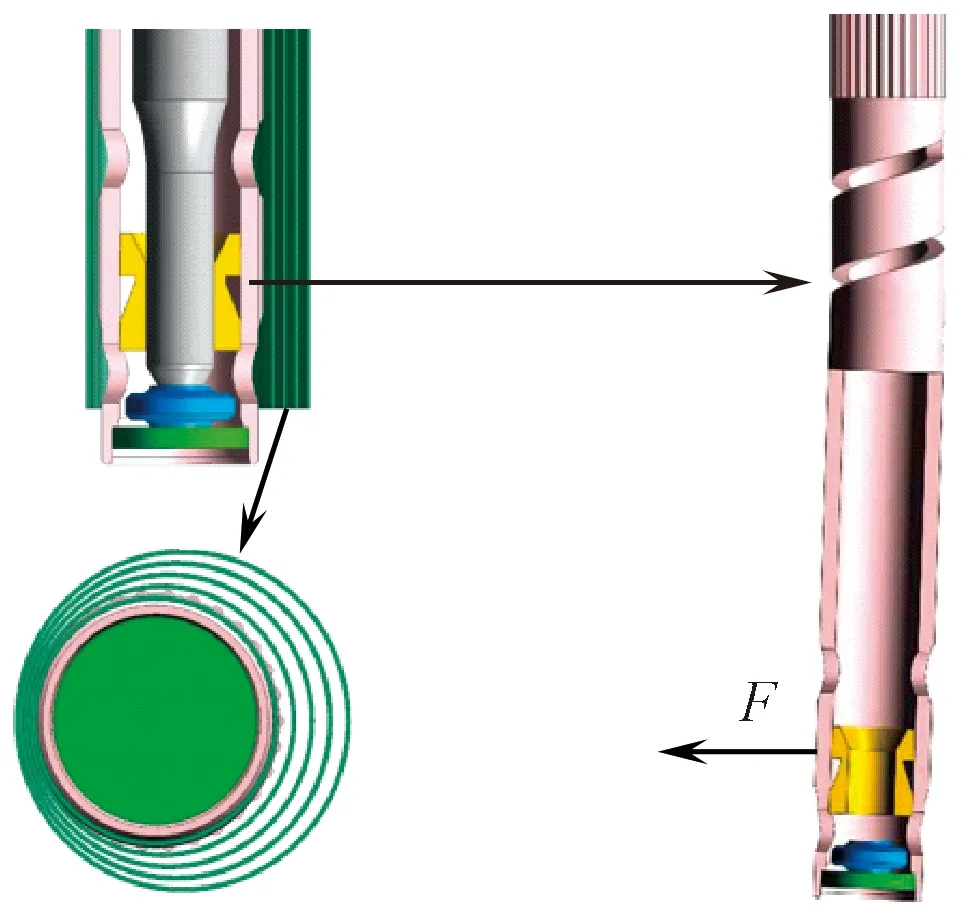
图2 弹性管底端振动示意图Fig.2 Vibration diagram of bottom of elastic tube
减振弹性管底部振动幅度A的计算公式为
式中:l2、l3为弹性管相应段的长度,mm;F为转子由滑动轴承传递给弹性管的激振力,N。
结合以上公式并通过实验研究表明,随着槽宽c的减小,壁厚h、螺距p、弹性模量E的增大,弹性管刚度增加,底部振幅降低[2-3],可见弹性管刚度和底部振幅2个目标之间是相互制约的,因此,本文提出以遗传算法来解决刚度和振幅多目标相互冲突的问题,结合径向基神经网络(RBF)近似模型,并利用遗传算法的随机性和隐含并行性,对弹性管模型进行多目标参数优化,从而获得给定参数区间的最优解集,达到锭子下弹性锭胆系统弹性管的最优性能。
2 弹性管多目标优化模型
2.1 弹性管优化目标选择
由上述分析可知,对于竖直悬臂梁结构的弹性管来说,降低弹性管刚度:一方面代表弹性管拥有更好的轴径向弹性,有利于下锭胆系统的弹性减振;而另一方面又增大了弹性管的底部振幅。表明弹性管刚度和底部振幅 2个目标之间是相互制约的,因此,多目标优化模型以弹性管刚度和底部振幅为2个目标函数,从二者之间找到最优配置,达到既能降低弹性管刚度,增加弹性,又能保证其底部振幅较小的性能最优选择。
2.2 优化问题数学模型构建
选取弹性管的主要影响参数槽宽c、螺距p、弹性模量E、壁厚h为设计变量,其中螺旋槽的槽宽取值范围设定为0 ~ 2 mm;由于目前新型平锭底结构型锭子中心距和支承轴承尺寸的限制,螺距p取值范围设定为6~12 mm;而壁厚取值范围设定为1~4 mm;材料的弹性模量取值范围设定为200 ~ 210 GPa;由于弹性管要承受自动落纱的轴向冲击力,以及高速旋转过程中的不平衡力对弹性管开螺旋槽部分的矩形弹簧造成剪切应力[5],剪切应力应满足以下关系:
式中:τmax为最大轴向载荷下开螺旋槽部分矩形截面内侧所产生的最大扭转应力,N;p为螺距,mm;D0为弹簧中径,mm;Fn为弹性管承受的轴向力,N;应力系数β2与矩形截面高宽比Φ(即(p-c)/h)和卷绕比D0/h有关,如表1所示;[τ]为许用剪切应力,视弹簧材料及受载情况而定。
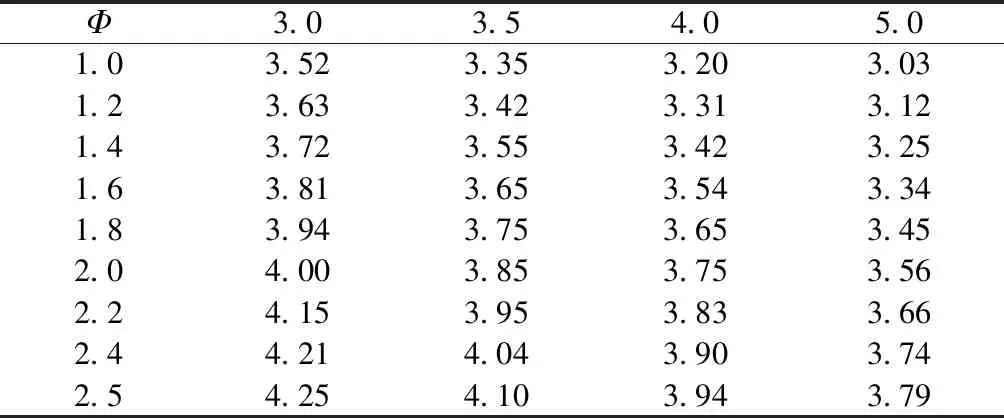
表1 不同卷绕比下应力系数β2值Tab.1 Stress coefficient β2 at different winding ratios
2.3 优化流程
为以尽可能少的试验次数得到有效的试验数据来构建近似模型,采用试验设计方法生成样本点。首先,在MatLab仿真建模软件中建立参数化数学模型,采用拉丁超立方设计方法生成设计变量样本点后,调用数学模型进行数值分析,获得离散的仿真值,然后结合近似模型技术,构建RBF近似模型,并检验近似模型精度。最后以抗弯刚度Jeq和底部振幅A最小为目标,在神经网络模型上进行寻优,得到Pareto最优解集。
3 近似模型构建及优化研究
3.1 RBF神经网络近似模型
近似模型方法是一种通过对具有代表性的局部点进行试验,拟合局部范围内因素与结果间的函数关系,取得各因素最优水平值的方法,适宜解决非线性数据处理的相关问题。常用的近似模型主要包括响应面法(RSM)、克里格模型(kriging)、神经网络模型(RBF/EBF)等[6-7]。通过对优化目标构建几种近似模型发现,RBF神经网络近似模型能够使优化目标近似精度达到可接受水平,其具有很强的逼近复杂非线性函数的能力和较强的容错功能,即使样本中含有“噪声”输入,也不影响模型的整体性能。
3.2 弹性管神经网络模型构建
本文采用拟合平均相对误差值E和复相关系数R2来衡量近似模型对试验数据的拟合程度。平均相对误差值E越小,代表可信度越高。R2值在0~1之间,如果R2值越接近1,则代表近似模型具有较高可信度[7]。通过拉丁超立方设计方法生成46个样本点,采集到一组设计变量和目标值的样本数据,进而构建神经网络近似模型。图3、4分别示出弹性管抗弯刚度Jeq及其底部振幅A的神经网络模型。

图3 弹性管抗弯刚度径向基神经网络模型Fig.3 Radial basis neural network model of elastic tube bending stiffness. (a) Approximate model of groove width and elastic modulus with bending stiffness; (b) Approximate model of pitch and wall thickness with bending stiffness
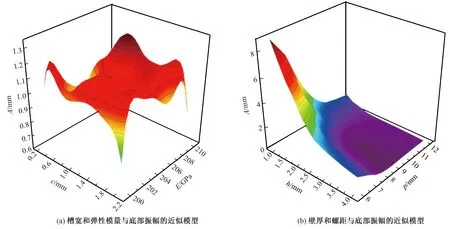
图4 弹性管底部振幅径向基神经网络模型Fig.4 Radial-based neural network model of bottom of elastic tube. (a) Approximate model of groove width and elastic modulus with bottom amplitude; (b) Approximate model of pitch and wall thickness with bottom amplitude
为检验近似模型的精确度,采用随机采样方法在样本空间重新取23个样本点拟合平均相对误差值E和复相关系数R2值。图5、6示出刚度和振幅实际仿真与近似模型预测值拟合对比。其中对角线表示预测值等于仿真值,红色点表示实际仿真样本点,蓝色水平线表示进行误差分析的样本点所对应响应的均值[8]。当实际仿真的样本点落在与预测值相等的对角线上,且与对角线重合越紧密,就说明近似模型越可靠。结合平均相对误差和R2值误差检验结果(见表2)与图5、6可知,该近似模型预测值可代替实际响应值,各目标值的平均相对误差值和R2均达到可接受水平。说明神经网络近似模型能满足拟合精度要求。

图5 刚度Jeq实际仿真值和近似模型预 测值拟合对比Fig.5 Comparison of actual simulation value of stiffness Jeq and approximate model prediction value
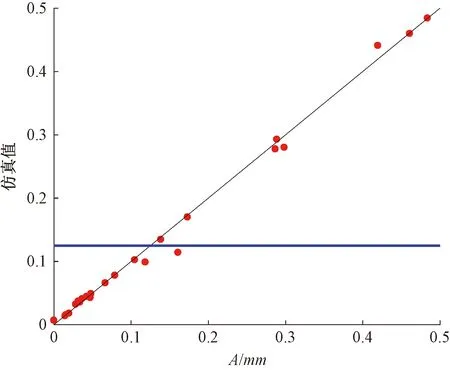
图6 振幅A实际仿真值和近似模型预测值拟合对比Fig.6 Comparison of actual simulation value of amplitude A and approximate model prediction value

表2 平均相对误差和R2值误差检验Tab.2 Average relative error and R2 value error test
3.3 弹性管参数优化及多目标结果分析
多目标优化算法的类型很多,其中,NSGA-II 遗传算法是在NSGA算法基础上进行改进得到的,该算法导入了“拥挤距离”和“拥挤距离排序”,可使计算结果在目标空间内比较均匀地分布,保证种群的多样性;还采用了精英策略将父代种群跟子代种群合并,保留父代优良个体,共同竞争产生下一代种群,防止Pareto最优解丢失[9-10]。
在多目标优化问题中,各目标响应值往往相互冲突,某个目标期望值的提高可能会引起其他目标值的降低,同时使多个目标达到最优一般是不可能的[11],因此,优化解不可能是单一的解,而是一个解集,称为Pareto最优解集。Pareto最优解集在对应的目标函数空间的像称为Pareto前沿。
在Isight平台上将上述各响应值作为优化目标,对构建的减振弹性管近似模型进行多目标优化,优化算法选择NSGA-Ⅱ遗传算法,设置初始种群为20,遗传代数为60,交叉率为0.9,计算消耗时间短,提高了计算效率,最终得到Pareto最优解集。
图7示出对x、y轴取对数后的Jeq和A的Pareto前沿图,黑色点表示可行解。可以看出,弹性管抗弯刚度Jeq和底部振幅A成反比关系,随着抗弯刚度的增加,底部振幅逐渐减弱。
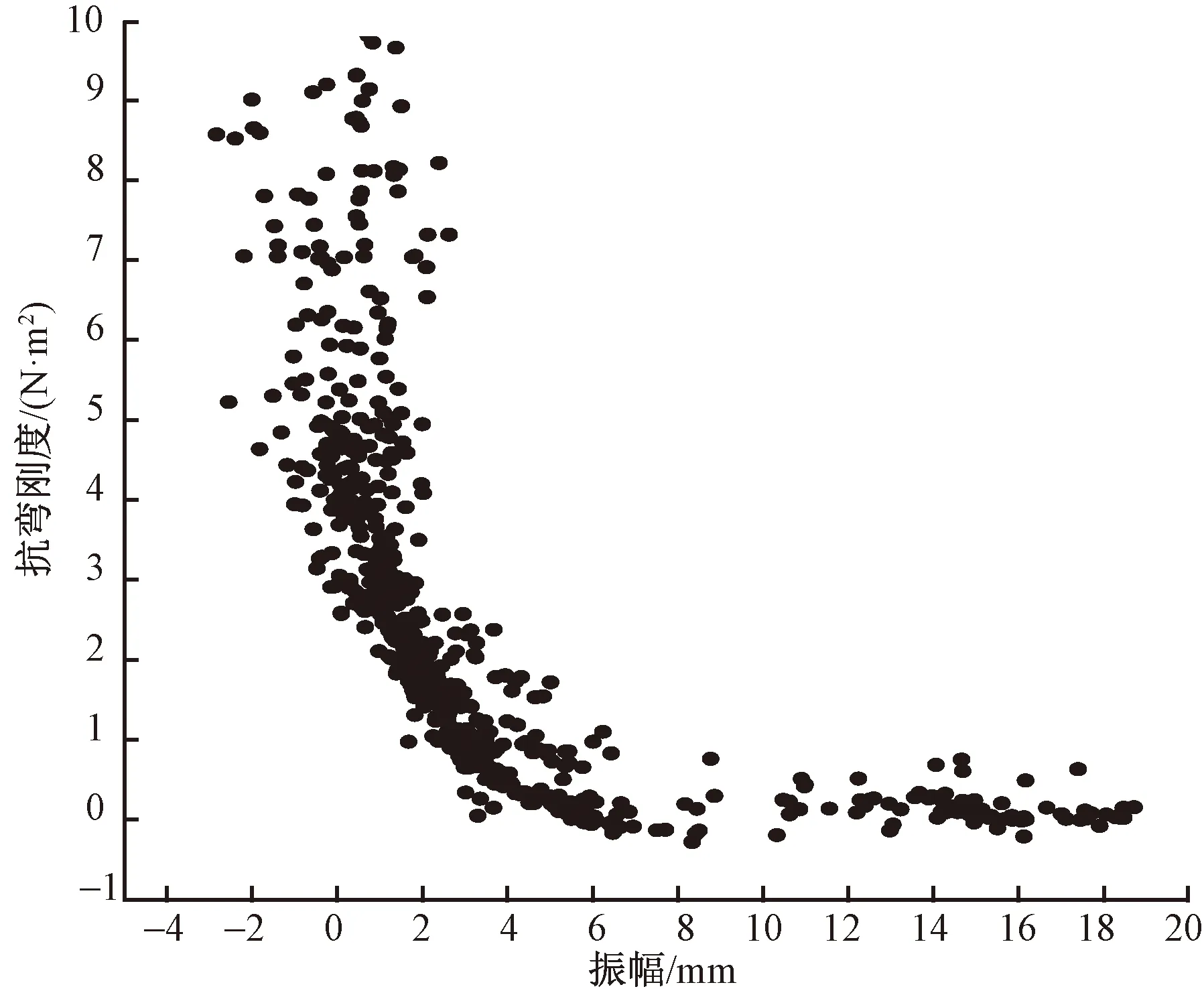
图7 抗弯刚度Jeq和底部振幅A的Pareto前沿图Fig.7 Pareto front of bending stiffness Jeq and amplitude A
虽然根据Pareto前沿图分析了各目标之间的变化关系,得到了弹性管各性能指数之间的关系,但由于目标函数间是相互矛盾冲突的,无法衡量Pareto最优解之间的优劣。在实际设计时,设计者需要基于相关工况,对目标重要性进行权衡,选择合适的最优解,最后通过实例验证该方法的可行性,选择合适的优化结果[12]。本文给出1组可行解作为优化算例,以此来体现优化结果的有效性。弹性管优化前后结果对比如表3所示。
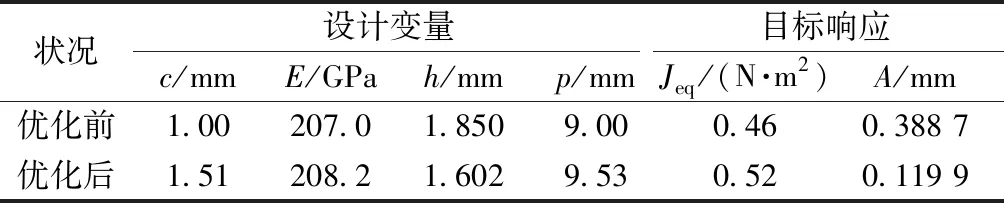
表3 优化前后弹性管工艺参数对比Tab.3 Comparison before and after optimization of elastic pipe process parameters
由表3可知,优化后的2个目标值性能均有所改善,综合分析可知,所选的可行解优化效果比较明显。其中,抗弯刚度Jeq由0.46 N·m2增至 0.52 N·m2,部分提高了弹性管的刚度;在不平衡力作用下的底部振幅A由0.388 7 mm降低到了 0.119 9 mm。 此优化结果表明,在刚度仅增加13%的前提下,振幅就降低了69%,说明优化后锭子吸振弹性管在保持弹性的同时,高速旋转下的稳定性也大幅提高。
通过仿真计算验证了锭杆高速运行下传递给弹性管的激振力对其底部振幅的影响,如图8所示。可以看出,优化后锭子在锭杆激振力作用下的弹性管底部振幅明显减弱,随着锭子高速旋转过程中锭速的增加,锭子会伴随着由之引起的不平衡力增加,而优化后的锭子弹性管底部振动相比优化前变化缓慢,说明优化后的锭子弹性管具有更加优良的性能,对吸振弹性管的高速下稳定性能有所提升。实验验证了优化方法的可行性和优越性,为锭子弹性管的结构设计提供了参数指导和优化方法的理论借鉴。
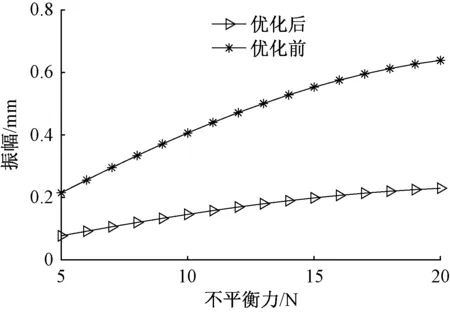
图8 弹性管优化前后底部振幅的变化Fig.8 Variation of bottom amplitude before and after optimization of elastic tube
4 结 论
以弹性管结构起主要影响的参数槽宽、螺距、弹性模量、壁厚为设计变量,以弹性管抗弯刚度和底部振幅为目标函数,基于径向基神经网络(RBF)构建近似模型使其达到可接受水平,并结合遗传算法对弹性管刚度及振动性能进行多目标优化设计,得到Pareto前沿提高了优化效率,通过得到的Pareto最优解集和Pareto前沿图,分析得到1组可行的最优解,验证此最优解发现,在弹性管刚度仅增加13%的前提下,振幅就降低了69%,说明优化后锭子吸振弹性管在保持弹性性能的同时,底部的振幅明显减弱,锭子旋转过程中传递的不平衡力引起的振动得到改善,使稳定性增加。

