纬平针棉针织物平幅丝光条件与其线圈结构的关系

尉腾祥， 李 敏， 彭虹云， 付少海

(1. 江苏省纺织品数字喷墨印花工程技术研究中心， 江苏 无锡 214122； 2. 生态纺织教育部重点实验室(江南大学)， 江苏 无锡 214122)

丝光是棉织物前处理过程的重要步骤，在浓碱和受力条件下针织物线圈形态会发生变化，从而引起性能的改变。通过丝光可极大提升针织物的尺寸稳定性、弹性、柔软性、舒适性，增强针织物对染料的吸附能力和吸湿性能，提高织物的强力、延伸度，改善棉针织物缩率大和易变形等缺点[1-2]。圆筒丝光是常用的丝光方式，具有成本低、织物无边疵等优点，但存在扩布时布面歪斜、接触机械阻力形成吃碱反应不匀的问题，平幅丝光可避免敏感薄形织物在圆筒丝光机丝光处理时线圈发生的微型变形等问题[3]。

在针织物平幅丝光方面，国内外研究主要集中在丝光工艺对织物强力、湿热阻以及尺寸稳定性的影响等方面：汤根娣等[4]研究了丝光条件对亚麻/棉混纺针织面料形态和强力的影响；胡萍等[5]研究了纤维素酶对丝光麻织物抗刺痒性能的影响；Ayatollahi等[6]研究了冷丝光工艺对夏季棉面料舒适性及力学性能的影响；Moghassem等[7]研究了丝光时间、氢氧化钠质量浓度、温度和张力等对平纹棉针织物尺寸稳定性的影响；Park等[8]研究了织物紧度、松弛处理和纱线捻度对平纹织物尺寸稳定性的影响。然而，针织物由线圈组成，在不同条件下线圈形态会发生变化，从而引起性能的改变，因此，研究丝光条件对织物线圈形态变化的影响十分有必要。

纬平针棉针织物是针织物中结构最简单的织物，横向延伸性大，易变形和脱散，因此，本文采用纬平针棉针织物为研究对象，在双向拉伸条件下，研究丝光过程中张力、氢氧化钠质量浓度、温度、时间对位移矢量、圈距、圈高、形态系数、剪切角等结构参数的影响规律，获得较佳的平幅丝光工艺条件。

1 实验部分

1.1 材料与设备

织物：漂白单面精梳纯棉针织物，纱线线密度为32 tex；织物面密度为140 g/cm2，圈距为 0.7 mm，圈高为0.5 mm，线圈长度为0.72 mm，纱线有效直径为0.18 mm， 绍兴海强针织厂。

试剂：氢氧化钠、冰醋酸，分析纯，国药集团化学试剂有限公司。

1.2 实验方法

将20 cm×20 cm的漂白单面针织物固定在丝光架上，在其中心区域划出14 cm×14 cm的区域，将针织物分为由不同节点组成的7 mm×7 mm方形单元，以方形单元作为研究对象，如图1所示。

图1 实验丝光架Fig.1 Experimental mercerizing device

织物在双向拉伸时所受张力的大小用扩幅表示，将针织物双向分别拉伸扩幅5%、10%、15%后，通过织物节点受力前后的位置和方向变化绘制位移矢量场。

丝光工艺流程：配制碱液→绷布(不同横纵向同时扩幅)→浸碱(不同氢氧化钠质量浓度、温度、时间)→热水洗(浴比为1∶20、60 ℃、4 min)→体积分数约为2%的醋酸中和→温水洗(2 min)→冷水洗(2 min)→剥离丝光架→烘干(60 ℃)。

1.3 测试方法

1.3.1 线圈参数测试

用游标卡尺测量织物节点处线圈的圈距和圈高，每个单元测量10次，取平均值。位移比计算公式为

式中：p为位移比，%；L0为织物处理前长度，m；L1为织物处理后长度，m。

1.3.2 形态系数测试

形态系数由圈高和圈距的比值表示，用游标卡尺测量圈高和圈距后，计算形态系数的值。

1.3.3 剪切角测试

剪切角是指织物单元受力后与拉伸方向形成的夹角，用剪切角变化来描述织物形变的程度。剪切角α示意图如图2所示。用万能量角器测量角α的大小，每个角度测量10次，取平均值即为线圈的剪切角。

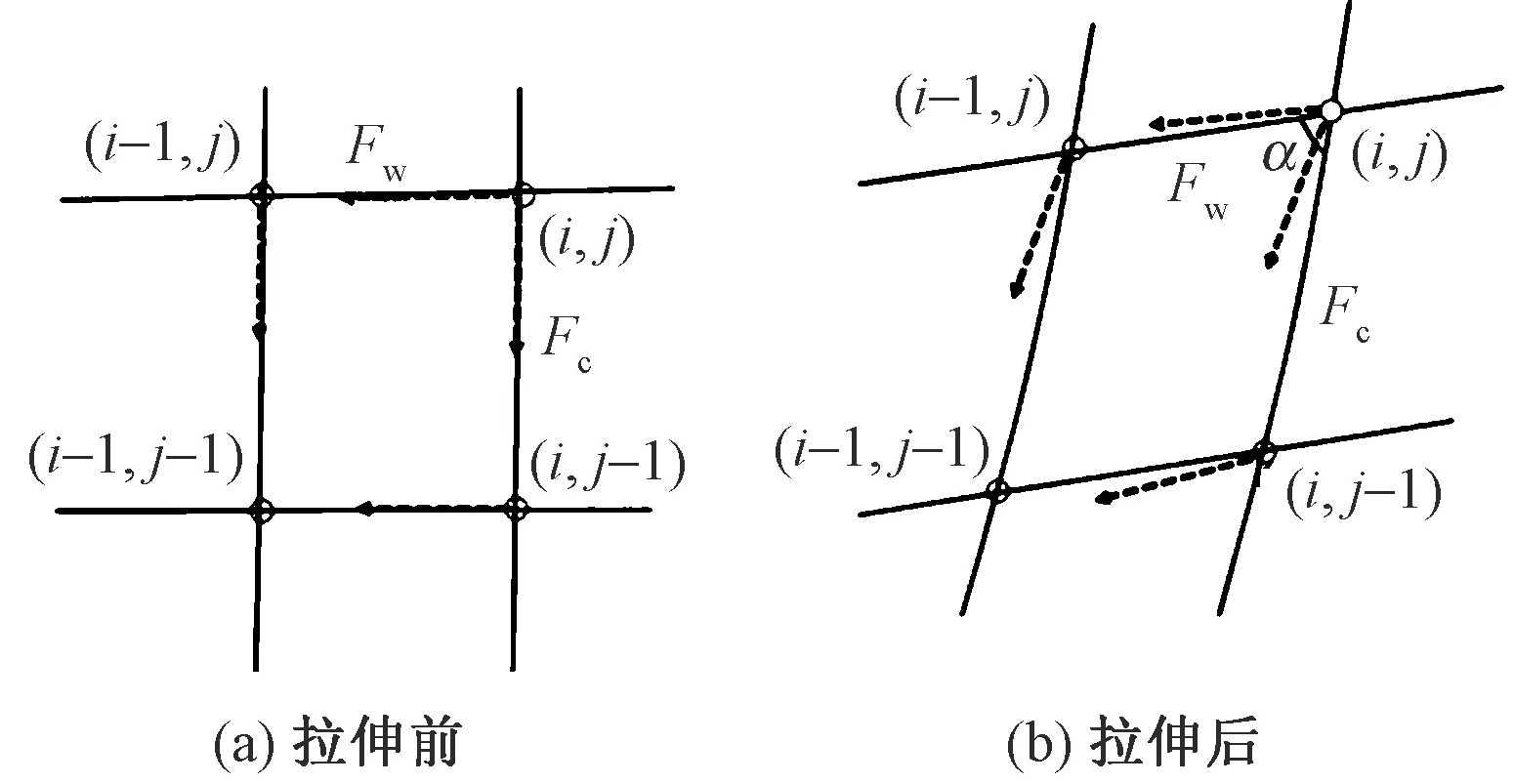
注：图中(i, j)为单元格的坐标； Fw和Fc 为织物受到的不同方向的拉力。图2 剪切角示意图Fig.2 Diagram of coil shear angle. (a) Before stretch; (b) After stretch

2 结果与讨论

2.1 拉伸张力的影响

图3示出不同拉伸张力扩幅时整个针织物的节点向量场。向量的起点和终点分别表示节点初始和变化后的位置，箭头的方向表示节点的位移方向。结果表明，织物整体变形沿轴向对称，对称中心附近的节点主要以单向位移为主，与对称轴平行且伴随微小位移；由于纱线之间存在摩擦以及不同位置处线圈受弯曲力矩大小不同，在织物边缘处，线圈单元发生歪斜等大变形行为。在不同拉伸张力下，节点的位移向量表现出不同的大小和方向[9-10]，使得织物不同区域呈现不同的变形。由图3还可发现，在节点向量场中出现位移比小于50%的椭圆区域(以下椭圆区域均指位移比小于50%)，随着拉伸张力的增加，椭圆区域面积由占整个试样的45.78%降低到24.39%。该结论表明，随着拉伸张力的增加，拉伸织物的小位移节点变少。

图3 不同拉伸扩幅条件下织物的向量场Fig.3 Vector field of fabric at different tensile extensions

由于织物节点数量过多，故选取具有代表意义的节点观察圈高和圈距的变化趋势。图4示出中心线上不同拉伸张力扩幅条件下织物单元的圈距和圈高测量结果。研究发现：圈距和圈高的变化符合抛物线变化规律，拟合度均大于0.95；随着拉伸张力的增大，圈距和圈高都增大，但增加的程度不同。这主要归因于结构单元的初始取向不同，以及在横纵方向上线圈的变化能力不同[11]。

图4 不同拉伸扩幅条件下织物中心线上圈距和圈高Fig.4 Centralized coil spacing and height of fabric at different tensile extensions

通常织物受力变形时圈高和圈距会随之发生变化，因此，采用圈高和圈距的比值，即形态系数可较好地描述针织物的变形特点[12]。图5示出根据圈高和圈距的比值测出的不同拉伸张力条件下织物单元的形态系数。织物未拉伸时形态系数为1.400。由图5可知：随着拉伸张力的增大，形态系数呈梯度分布，最大的形态系数由1.048减小到1.028；当拉伸扩幅为5%时，中心区域的形态系数值在1.025～1.033之间，明显比拉伸扩幅为10%和15%时大。

图5 不同拉伸扩幅条件下织物的形态系数Fig.5 Shape coefficient of fabric at different tensile extensions

图6示出不同拉伸张力扩幅时织物单元的剪切角。可知，织物剪切角存在明显的递变规律。随着拉伸张力的增大，中心区域面积增加，边缘区域的最大剪切角减小，由89.3°减小为88.3°。圈距和圈高直接关系到织物横向和纵向的密度，是决定织物尺寸稳定性的重要因素[12-13]。实际实验过程中，在拉伸扩幅为10%、15%时，织物结构已发生微小的脱散，线圈变形严重。以上实验结果表明，张力对织物线圈结构参数影响较大，本文在选定的3个张力条件下，最佳的张力条件为双向拉伸扩幅5%。

图6 不同拉伸扩幅条件下织物的剪切角Fig.6 Shear angles of fabric at different tensile extensions

2.2 氢氧化钠质量浓度的影响

图7示出不同氢氧化钠质量浓度时织物的节点向量场。可以看出，随着氢氧化钠质量浓度的增加，椭圆区域面积先增加后变化不大，在氢氧化钠质量浓度为200 g/L时面积达到最大。

这是因为随着氢氧化钠质量浓度的升高，纤维发生明显的溶胀，纤维表面不均匀变形被消除，且可均匀地分担外力，使线圈变形比较均匀。

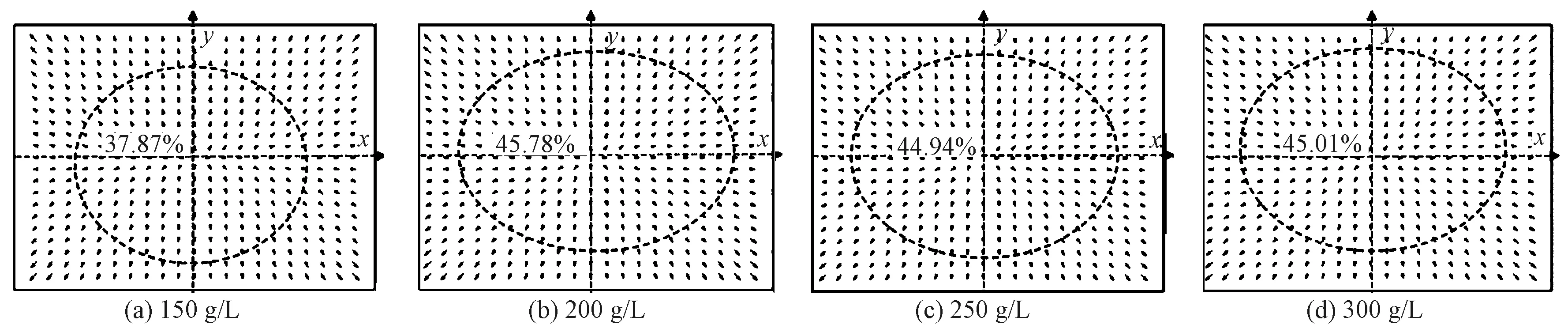
图7 不同氢氧化钠质量浓度时织物的向量场Fig.7 Vector field of fabric at different NaOH mass concentrations

图8示出不同氢氧化钠质量浓度时织物单元的圈距和圈高测量结果。研究发现：圈距和圈高的变化符合抛物线变化规律，拟合度均大于0.94；随着氢氧化钠质量浓度的变化，圈距和圈高变化范围不大；在氢氧化钠质量浓度为200 g/L时，圈距和圈高均取得最大值。

图8 不同氢氧化钠质量浓度时织物的圈距和圈高Fig.8 Coil spacing and height of fabric at different NaOH mass concentrations

图9示出不同氢氧化钠质量浓度时织物单元的形态系数。可看出：当氢氧化钠质量浓度为 200 g/L时，中心区域的形态系数值在1.025～1.033 之间，明显较其他质量浓度的大。

图10示出不同氢氧化钠质量浓度下织物单元的剪切角。可以看出：从织物中心区域到边缘区域，剪切角存在明显的递变规律；当氢氧化钠质量浓度为 200 g/L 时剪切角最大，为89.3°。

以上分析表明，氢氧化钠质量浓度对织物线圈结构参数的影响也较大，在其为200 g/L时，织物收缩与拉伸的程度大致相等，线圈均匀程度较高，因此，较佳的平幅丝光氢氧化钠质量浓度为200 g/L。

图9 不同氢氧化钠质量浓度时织物的形态系数Fig.9 Shape coefficient of fabric at different NaOH mass concentrations

图10 不同氢氧化钠质量浓度时织物的剪切角Fig.10 Shear angles of fabric at different NaOH mass concentrations

2.3 丝光温度的影响

图11示出不同丝光温度时织物的节点向量场。可知，随着温度的变化，椭圆区域面积在50 ℃时达到最大(45.78%)。

图12示出不同丝光温度时织物单元的圈距和圈高。可以看出，圈距和圈高的变化符合抛物线的变化规律，拟合度均大于0.94。在丝光温度为 50 ℃ 时，圈距和圈高均是最大的。

图11 不同丝光温度条件下织物的向量场Fig.11 Vector field of fabric at different mercerization temperatures

图12 不同丝光温度条件下织物的圈距和圈高Fig.12 Coil spacing and height of fabric at different mercerization temperatures

图13示出不同丝光温度条件下织物单元的形态系数。可知：随着温度的变化，最大形态系数值由1.048减小到1.010；当温度为50 ℃时，中心区域的形态系数值在1.025～1.033之间，明显比温度为40和 60 ℃ 时的大。

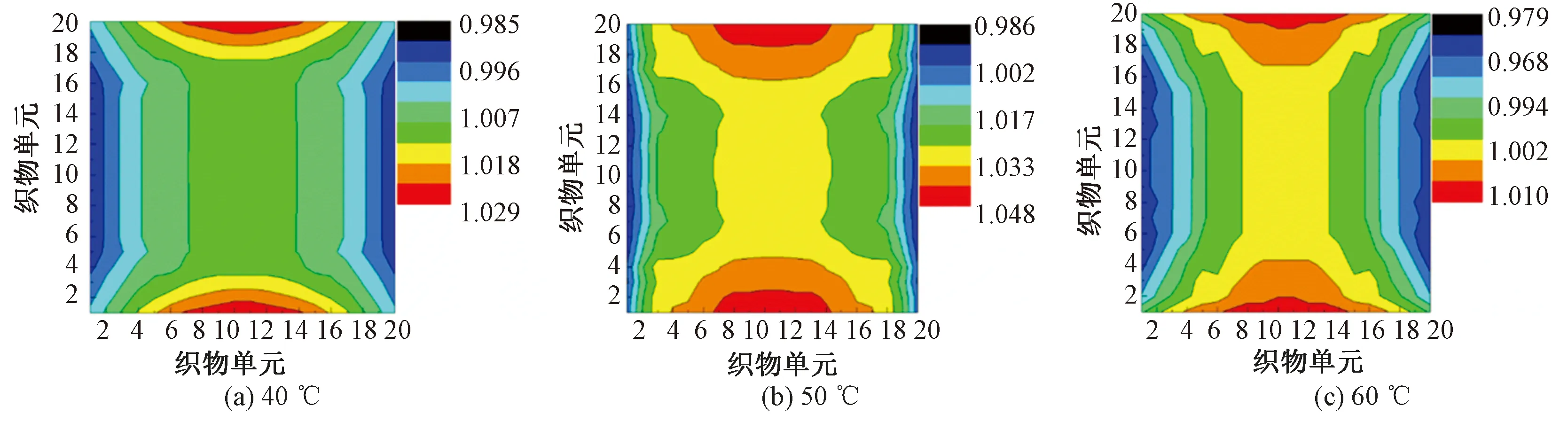
图13 不同丝光温度条件下织物的形态系数Fig.13 Shape coefficient of fabric at different mercerization temperatures

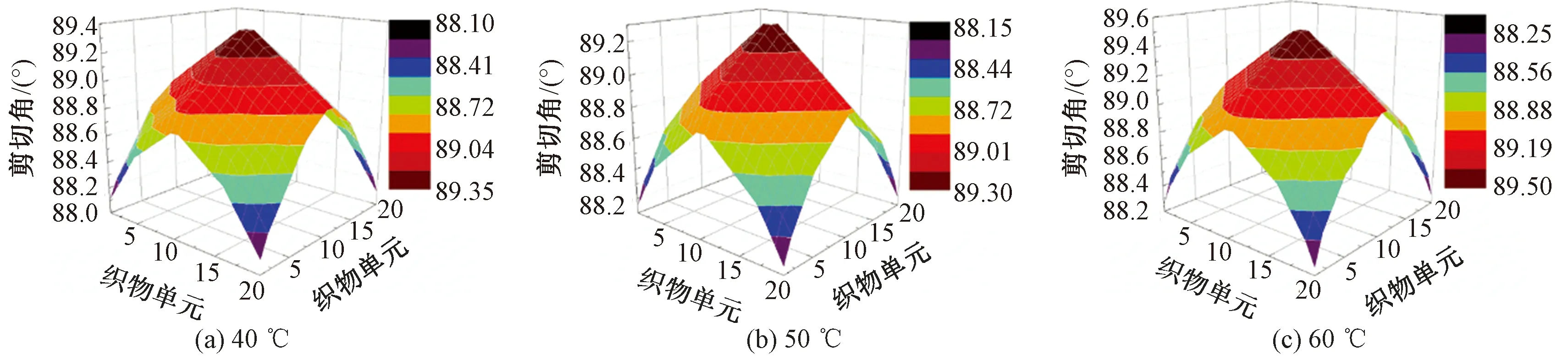
图14 不同丝光温度条件下织物的剪切角Fig.14 Shear angles of fabric at different mercerization temperatures

图14示出不同丝光温度条件下织物单元的剪切角。结果表明，温度对织物单元的剪切角影响较小，中心区域的最大剪切角约为89.3°。

以上分析表明，适当的温度可提高丝光的效果，改善丝光线圈变化的均匀程度，温度太高或太低，会使线圈均匀程度下降，较佳的平幅丝光温度为 50 ℃。与丝光张力和氢氧化钠质量浓度的影响相比，丝光温度对织物线圈结构参数影响较小。

2.4 丝光时间的影响

图15示出不同丝光时间时织物的节点向量场。可知，随着时间的变化，椭圆区域面积发生变化，在时间为120 s时达到最大(45.78%)，此时，织物变形比较均匀。

图16示出不同丝光时间时中心线上织物单元的圈距和圈高。研究发现：圈距和圈高的变化符合抛物线变化规律，拟合度均大于0.95；在温度为 120 s 时，圈距和圈高都是最大的。

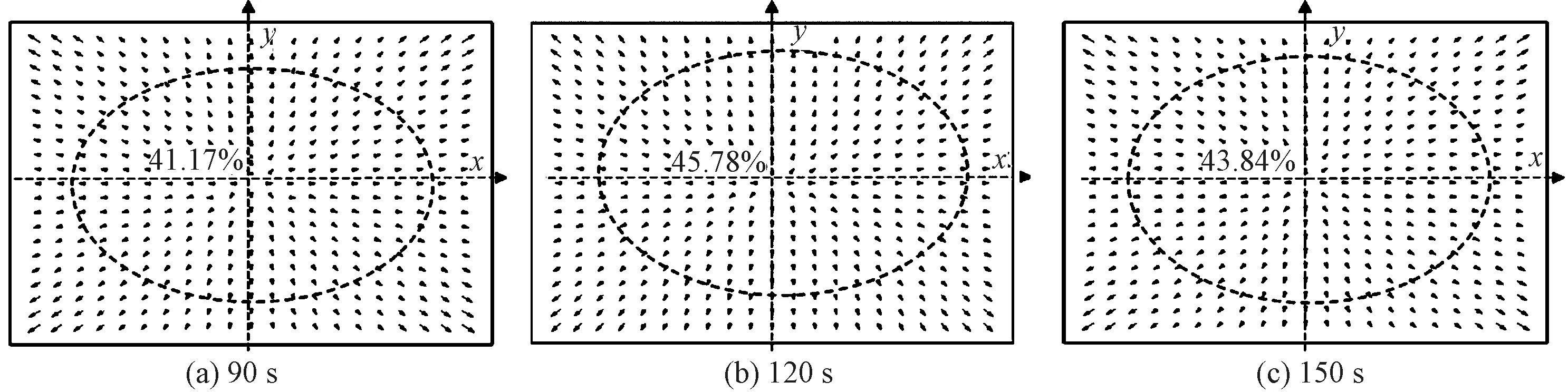
图15 不同丝光时间条件下织物的向量场Fig.15 Vector field of fabric at different mercerization time

图16 不同丝光时间条件下织物的圈距和圈高Fig.16 Coil spacing and height of fabric at different mercerization time

图17示出丝光时间对织物单元的形态系数的影响。可知：随着丝光时间的增加，不同时间下最大形态系数值由1.048减小到1.010；当丝光时间为120 s时，中心区域的形态系数值在1.025～1.033之间，明显比丝光时间为90和150 s时的大。

图18示出织物单元的剪切角。可知，随着丝光时间的变化，中心区域和边缘区域剪切角的变化均不明显。

图17 不同丝光时间条件下织物的形态系数Fig.17 Shape coefficient of fabric at different merceization time

图18 不同丝光时间条件下织物的剪切角Fig.18 Shear angles of fabric at different mercerization time

以上分析表明，丝光时间关系到丝光效果的好坏，时间太短丝光效果不彻底，时间太长会使线圈均匀程度降低，因此，较佳的平幅丝光时间为120 s。

3 结 论

本文研究了针织物在不同丝光条件(拉伸张力、氢氧化钠质量浓度、温度、时间)下线圈结构变化，得到如下结论。

1)丝光处理时张力和氢氧化钠质量浓度对线圈结构的影响很大，而丝光温度和时间对线圈结构的影响较小。

2)丝光处理后织物向量场中各节点的位移大小与方向会发生变化，使得织物不同区域呈现不同的变形，且出现织物形变较小(位移比小于50%)的椭圆形区。

3)织物圈距和圈高的变化符合抛物线变化规律，形态系数呈梯度对称分布，剪切角存在明显的递变规律。在双向拉伸扩幅为5%、氢氧化钠质量浓度为200 g/L、温度为50 ℃、时间为120 s时，形变较小的椭圆面积达到最大为45.78%，此时织物圈距和圈高也最大，剪切角变化更加平缓，同时形态系数更加均匀。