织物纹样特征提取与匹配方法比较
汪 会, 孙 洁, 丁笑君,2, 龙 颖, 邹奉元,2,3
(1. 浙江理工大学 服装学院, 浙江 杭州 310018; 2. 浙江理工大学 浙江省服装工程技术研究中心, 浙江 杭州 310018; 3. 浙江省服装个性化定制协同创新中心, 浙江 杭州 310018)
计算机图像识别与匹配技术应用于服饰纹样的分类、识别与快速调用[1-2],为服饰纹样的数字化设计提供了有效途径。织物纹样识别的关键是寻找合适、有效的特征用于识别[3]。国内外学者提出了多种用于图像识别的特征描述方法:曹霞等[4]在进行蕾丝花边层次匹配检索时,应用快速鲁棒性尺度不变特征(SURF)作为第3层次的匹配依据;路凯等[5]应用视觉词袋模型进行羊绒羊毛纤维的鉴别时,将尺度不变特征变换(SIFT)关键点转换为视觉单词表示纤维特征;丁笑君等[6]用SIFT算法获得畲族服装样图关键点分布,得到不同类别畲族服装的关键设计区域和排序;陈金广等[7]讨论了旋转、尺度和噪声变化下纹样匹配方法发现,SIFT与SURF算法具有较好的适应性。
虽然,以SIFT与SURF为代表的局部描述子在织物图像识别检索中有较好的适用性,但在复杂图像配准过程中,有效的局部特征点抓取数量存在不足,且准确匹配率不高,因而复杂织物图像的特征提取与匹配问题仍存在挑战[3]。与上述特征提取方法不同,基于二值特征的特征描述子具有匹配速度快,存储要求内存低等特点,在复杂图像特征提取与匹配问题中更具优势。
本文将二进制鲁棒不变可扩展关键点(BRISK)算法和随机抽样一致(RANSAC)算法引入织物纹样特征提取与匹配问题中,讨论尺度、旋转、模糊、光照、褶皱5个变化因素下织物纹样图像特征提取与匹配方法。从特征点数量、准确匹配率及匹配时间3个方面,将BRISK与SIFT、SURF算法进行比较分析,为复杂织物纹样的自动识别提供参考。
1 实验与图像预处理
1.1 图像采集
江崖海水纹是具有代表性的中国传统纹样之一,多为对称式独立纹样,纹样构图复杂,元素形态多样[8]。本文通过数码印花的方式获取30 cm×20 cm 的涤纶厚缎江崖海水纹面料。为探讨尺度、旋转、模糊、光照、褶皱5个因素下纹样匹配差异,实验过程中排除了外界不确定光源对其他因素的干扰,选取DiGiEye数字测色仪和VIZOO X-Tex型三维面料扫描仪采集图像。其中DiGiEye数字测色仪的相机型号为Nikon D90,两侧有D65光源,系统顶部为凹凸弧面漫反射光,可使面料均匀受光。同时,因DiGiEye漫反射均匀光照射时面料褶皱立体感不明显,故选用VIZOO X-Tex型三维面料扫描仪获取褶皱状态下面料图像。
江崖海水纹获取流程如图1所示,可得到基准及尺度、旋转、模糊、光照、褶皱5种变化的图像。每种图像以1∶4的比例依次缩小,可获得3种尺度变化图像;以30°为间隔顺时针旋转,得到6种旋转变化图像;通过在D65光源上遮挡不同透光程度的材料,拍摄得到4种光照强度的图像;通过调节相机焦距,获得4种模糊处理的图像;在面料下方放置不同高度形状的支撑物得到4种褶皱效果图像。

图1 江崖海水纹获取流程Fig.1 Process of obtaining jiangya sea water patterns
图2示出3例江崖海水纹原图。本文实验选择3例经典江崖海水纹进行上述的图像变换,获得 5个变化因素下人物纹样图像。

图2 3例江崖海水纹原图Fig.2 Original image of 3 kinds of jiangya sea water patterns
1.2 数据分析平台
实验平台采用Visual Studio 2017搭建OpenCV 2.4.9 计算机视觉库,电脑操作系统为Windows 10,CPU为Inter(R) HD Graphics 4600,显存为2 GB。
1.3 图像预处理
本文图像处理部分以1#为例,在保留图像有效信息的前提下,为提高图像处理速度,将采集图像的分辨率统一为300像素,并转化为灰度图像,如图3 (a) 所示。此外,由于面料图像在纱线间隙处颜色偏暗、柱状纱线上颜色较亮易产生脉冲噪声[9],如图3 (b)所示。采用中值滤波进行预处理。过程为
g(x,y)=med{f(x-k,y-l),(k,l∈W)}
(1)
式中:f(x,y)、g(x,y)分别为原始图像和处理后图像;(x,y)为像素坐标;W为窗口大小,实验中采用3×3的窗口,经中值滤波后获得的图像见图3 (c)。

图3 图像预处理Fig.3 Image preprocessing. (a) Grayscale processing; (b) Image noise; (c) Median filtering preprocessing
2 面料图像的特征提取与匹配
本文针对服饰纹样尺度、旋转和褶皱等形变状态下纹样与原始纹样的精确匹配问题展开讨论,提出BRISK算法用于复杂纹样的特征提取,并与常用在服饰纹样特征提取中的SIFT、SURF算法对比,最后通过欧氏距离匹配和RANSAC算法剔除错误匹配对,讨论3种算法对复杂织物图像特征提取与匹配的有效性。
2.1 图像特征提取
2.1.1 BRISK特征提取
BRISK算法提取特征过程中,首先采用 FSAT9-16 型角点检测器在连续尺度空间里找到的稳点极值点作为江崖海水纹样的特征点。采用自定义的邻域采样模式,将采样点进行两两组合,获得采样点对Ω,采用欧氏距离定义短距采样点对集S和长距采样点对集P如下:
S={(pi,pj)∈Ω|‖pi-pj‖<δmax}⊆Ω
(2)
P={(pi,pj)∈Ω|‖pi-pj‖>δmin}⊆Ω
(3)
式中,δ为尺度。
令L为长距采样点对集P的元素个数,g(pi,pj)为点对(pi,pj)的局部梯度集合,角点的特征方向定义为
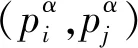
(4)

2.1.2 SIFT特征提取
SIFT特征描述算子具有尺度缩放、亮度、仿射变换保持不变的特性[5-6]。首先以图像建立高斯金字塔;然后利用高斯插分函数检测局部极值点,经过非极大值抑制去除低对比度的点,初步确定兴趣点;然后通过Hessian矩阵去除低对比度和不稳定的边缘的响应点,增强匹配稳定性;根据筛选出每个关键点邻域内的梯度方向,为其分配梯度方向和梯度模;最后组合成128维向量进行图像特征表达。
2.1.3 SURF特征提取
SURF算法确定特征点的过程中,先采用Hessian矩阵确定候选点,运用非极大抑制法和插值运算寻找和定位关键点[4],选取关键点的主方向是采用harr小波特征,以关键点为中心的邻域内统计其邻域像素。在关键点周围取一个边长为2s(s为所检测特征点尺度)的正方形框,将该框分为16个子区域,每个子区域统计25 像素的水平方向和垂直方向的4个harr小波特征,最后在每个子区域中生成特征点的64维特征描述子进行图像特征表达。
2.2 特征点匹配与筛选
本文在特征提取后,采用欧氏距离进行匹配计算。关键点对的特征描述符由2个n维向量a(xi1,xi2,…,xin)与b(xj1,xj2,…,xjn)表示,其欧氏距离的计算公式为
(5)
式中,n为特征点描述符的维数。然后计算最小欧氏距离d1和次小欧氏距离d2的比值k,当k小于比例阈值k0时,则认为匹配成立[10]。
初步匹配后,仍存在大量的错误匹配情况。尺度缩放时SIFT算法的错误匹配如图4所示。图中右侧部分为进行尺度缩放比为1∶4的SIFT特征提取匹配时出现的错误匹配。描述子仅描述特征点局部信息,故在复杂且伴有重复纹理的纹样匹配时,易出现匹配错误。

图4 尺度缩放时SIFT算法的错误匹配Fig.4 SIFT algorithm false match in scale zooming
初步匹配后,采用RANSAC算法剔除错误匹配对[11]。RANSAC算法能鲁棒地估计模型参数,常用于滤除图像匹配中的错误匹配。该算法通过选取内点数量最多、误差最小的变换矩阵参数作为匹配图像之间的投影变换矩阵,从而剔除错误匹配对。
特征提取与匹配算法的匹配准确率越高,则算法鲁棒性越强。准确匹配率计算公式为
(6)
式中:M2为经过欧氏距离匹配后的准确匹配数;M1为RANSAC过滤的准确匹配数。经RANSAC剔除错误配对后的特征匹配效果提升明显,如图5所示。

图5 原图与模糊图像匹配效果Fig.5 Matching effect of original image and fuzzy image.(a) BRISK algorithm matching; (b) BRISK/RANSAC algorithms matching
3 结果与分析
3.1 阈值选取与分析
为获取合理匹配阈值k0,综合比较了不同阈值下的准确匹配数与准确匹配率。在匹配实验中,以4种褶皱变化为例,当k0取0.1、0.2时,无法获得匹配点;因此,k0依次取值为0.3、0.4、0.5、0.6、0.7、0.8、0.9。7个水平下褶皱变化的平均匹配数据如表1 所示。可见:BRISK算法提取特征点数多于SIFT、SURF算法;随着阈值k0增大,3种算法所有匹配数和准确匹配数都呈上升趋势;当k0≤0.5时,3种算法的准确匹配率均较高,但配对数及准确匹配数值较低,特别是BRISK算法中有大量特征点但没有成功匹配,说明设定的比例阈值k0≤0.5时,有大量的匹配点对被排除在外,对特征图像特征表达存在不足;当k0≥0.6时,准确匹配率随k0的增大而减小,且随着k0的增大,BRISK算法获取的准确匹配数增加幅度明显大于SIFT、SURF算法。综合考虑3种算法的合理阈值选取,最终采用阈值k0为0.6进行匹配比较实验。
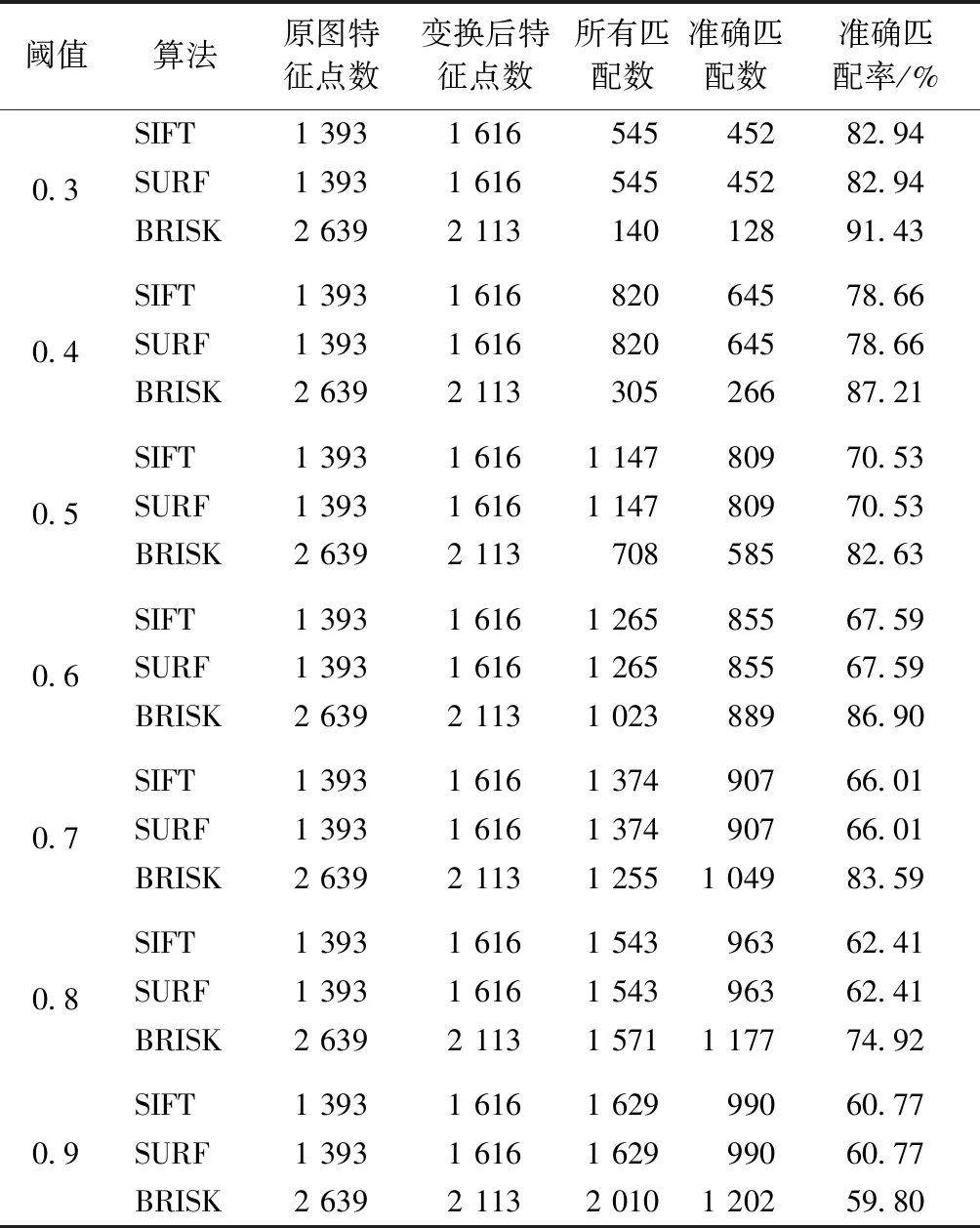
表1 褶皱状态下不同比例阈值的平均匹配结果对比Tab.1 Comparison of matching results of different ratio thresholds at drape state
3.2 匹配结果分析
表2对比了3种算法综合3例江崖海水纹在阈值k0=0.6时的平均匹配效果。可知,BRISK算法对每一类变换的准确匹配率均最高,在旋转变换匹配实验中,3种算法的匹配率都达到80%以上,SIFT、SURF、BRISK算法的平均准确匹配率分别为82.60%、81.38%、87.10%。在光照强度变换时,BRISK算法对光变化不敏感,准确匹配率较高且稳定。在褶皱变换匹配实验中,因特征点位置发生变化,匹配点对间的最小欧氏距离和次小欧氏距离的比值k变动较大,导致很多特征点对不符合筛选条件。故虽然BRISK算法匹配率最优,但3种算法的平均准确匹配率均未达到70%。

表2 3种算法准确匹配率比较Tab.2 Comparison of matching accuracy of three algorithms
表3示出5种变化下不同算法对江崖海水纹样的平均匹配时间对比结果。可见,BRISK算法计算速度明显优于SURF和SIFT,BRISK的平均匹配时间为0.551 s,SIFT和SURF算法的平均匹配时间分别为1.336、1.435 s。

表3 5种变化下不同算法的匹配时间比较Tab.3 Comparison of matching time of different algorithms under five kinds of changes s
3.3 多样本匹配结果比较
为进一步验证BRISK算法在织物纹样特征提取与匹配问题中的适用性,本文选择了2例织物纹样为样本进行比较分析,织物纹样原图如图6所示。

图6 织物纹样Fig.6 Fabric patterns.(a)Pattern A;(b)Pattern B
采用相同的样本采集方法获取织物纹样的基准、尺度、旋转、模糊、光照、褶皱图像共44幅,进行基准与变化织物纹样的匹配实验,取k0=0.6,每类别的平均准确匹配率实验结果如表4所示。可见:BRISK算法的平均准确匹配率明显优于SURF和SIFT算法;织物纹样A和B在旋转、模糊和光照变化状态下,BRISK算法均高于80%,其中光照变化下平均准确区配率高于95%;在尺度、褶皱变化状态下,BRISK算法相较于SURF和SIFT算法优势明显。在A和B这2例织物纹样的5类变化匹配实验中,BRISK算法的平均准确匹配率均可保持在70%以上,所有实验的平均准确匹配率为86.3%。可见,BRISK算法在复杂织物纹样的特征提取与匹配中具有较好的适用性。

表4 5种变化下织物纹样A、B的平均准确匹配率Tab.4 Average correct matching rate of fabric patterns A and B under five variations %
4 结 论
针对复杂服饰纹样的特征提取与匹配问题,本文提出了二进制鲁棒不变可扩展关键点(BRISK)算法结合随机抽样一致(RANSAC)算法进行服饰纹样特征提取与匹配,通过构建连续的尺度空间,利用FAST9-16型角点检测器快速找到服饰纹样的稳定极值点作为特征点,并依赖可配置的圆形采样模式获得匹配结果,最终得到二进制BRISK描述子并进行图像特征表达。该方法有效解决了因织物图像旋转、模糊、光照、尺度、褶皱引起的匹配差异,且匹配速度更快,占用内存越小。通过实验证明了该方法在图像的准确匹配数及准确匹配率以及运算时间上均优于尺度不变特征变换(SIFT)、快速鲁棒性尺度不变特征(SURF)算法。在后续研究中将进一步将该方法运用于复杂服饰图案的识别与检索中。

