动态物流网络多目标优化模型及求解算法

王亚东，石 全，宋卫星，胡起伟

(陆军工程大学 石家庄校区装备指挥与管理系，河北 石家庄 050003)

0 引言

工程实际中，产品供应通常为间歇性和多阶段，例如，在(s，S)库存策略下，每当库存量低于阈值s时则进行补货；而在(R，Q)策略下，每间隔R段时间进行一次补货。因此，根据既定的消耗规律、维修方式和库存策略，可以确定在给定时间界限内的备件供应阶段数。可以看出，无论采用何种策略，产品的供应均分为多个阶段完成，由此构成了动态物流网络。在动态物流网络优化问题中如何将实际问题转化为数学模型，以及如何对复杂模型进行求解仍亟待解决。

关于物流网络优化问题，目前国内外均有相关研究。Wang等[1]以成本最小为目标研究了静态二级物流网络的分配问题，使用蚁群遗传混合算法对模型进行求解。De Keizer等[2]研究了易腐产品的物流网络选址分配问题，同样以成本最小为目标构建了线性规划模型。TANG等[3]以成本最小和CO2排放最少为目标建立物流网络的无容量设施选址多目标优化模型，采用ε-约束法求解模型。Yang等[4]考虑低碳资源的配置，提出一种新的碳税限制型城市物流配送网络规划模型。采用双线性非凸混合整数规划，并通过适当的线性化简化为纯线性混合整数规划进行求解。Soleimani等[5]研究了静态闭环物流网络选址分配问题，使用粒子群和遗传算法求解NP问题。周芳汀等[6]构建了带时间窗的地铁配送网络路径规划模型，采用随机变邻域和迭代搜索算法进行求解。Jeet等[7]以时间和服务水平为目标对物流网络分配问题进行研究，提出了基于线性化模型的精确式求解方案。

可以看出，一方面目前大部分研究集中在静态物流网络优化以及单目标优化，动态和多目标优化仍是热点和难点问题；另一方面，求解算法大多为精确式算法，此类方法过分依赖模型结构本身且很难求解非线性和非凸问题。多目标进化算法(Multi-Objective Evolutionary Algorithm, MOEA)是一种基于种群搜索的智能优化方法，属于元启发式算法。作为随机搜索算法，进化算法不需要梯度和解析的目标函数，因此适用于处理没有解析目标函数和无法得到目标函数梯度信息的优化问题；其次，因为进化算法是随机搜索方法，所以它们搜索全局最优解的能力比较强。因此，近些年来MOEA被广泛用于多目标优化问题。目前多目标优化算法可分为基于帕累托(Pareto-based algorithms)、基于分解(decomposition-based algorithms)和基于指标(indicator-based algorithms)的方法[8]。基于Pareto的方法通过比较不同解之间的支配关系，选出非支配解作为最优解，常用的算法有快速非支配排序遗传算法(non-dominated sorting genetic algorithm Ⅱ)[9]、多目标差分进化算法(multi-objective differential evolution algorithm)[10]、增强Pareto进化算法(strength Pareto evolutionary algorithm)[11]等；基于分解的算法通过标度函数聚合的目标，从而生成单个标量值，并通过指定一组分布良好的参考点来保持种群的多样性，从而指导个体同时搜索不同的最佳状态，常用的算法为MOEA/D[12]；基于指标的算法则是利用一个性能指标来指导进化过程中的搜索，常用的指标有IGD(inverted generational distance)、HV(hyper-volume)等[13]。

目前，多目标进化算法在处理静态多目标优化问题时应用较多也相对成熟，如何将其应用于动态优化问题仍有待探索。本文充分考虑物流网络优化中多目标、多阶段等特点，在差分进化框架基础上提出了相应的动态响应机制和进化策略以采用进化算法解决动态网络优化问题。

1 问题描述与建模

1.1 问题描述及假设

本文研究主要针对传统物流网络的节点选址问题和产品分配问题，属于选址—分配联合优化问题。经典物流网络由三级供应网络节点构成，即供应点、中转点和需求点。顾客在需求点产生产品需求，其需求量反馈给供应点。供应点根据顾客需求提供产品，产品经中转点向各需求点进行分配和供应。在供应过程中，根据实际需要决定开放中转点的数量。为同时保证物流网络的效率和经济性，在保证满足顾客需求的前提下，要求产品供应的时间最短和供应花费总成本最少。由于顾客对产品的消耗为离散规律，整个供应为多阶段的动态过程。

本文物流网络优化模型建立在以下假设之上：

(1)以某一类产品为研究对象；

(2)各阶段节点之间的产品运输成本均为已知，不同阶段运输成本可能不同；

(3)中转点的开放费用、库存费用、最大储备量均为已知，且不随时间变化；

(4)各阶段需求点的产品需求量和缺件损失已知，不同阶段各不相同；

(5)暂不考虑越级供应以及同级之间的横向供应。

1.2 参数说明

I为供应点的数量，i=1,2,…,I；

J为中转点的数量，j=1,2,…,J；

K为需求点的数量，k=1,2,…,K；

T为供应持续的周期数，t=1,2,…,T

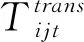
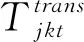
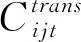
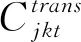
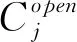
Uj为产品在第j个中转点的最大储备量。

决策变量：

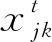
1.3 物流网络多目标优化模型

目标函数1：产品供应总成本最小，即

(1)

(2)

t=1,2,…,T；

(3)

t=1,2,…,T；

(4)

(5)

目标函数2：产品供应总时间最短，即

t=1,2,…,T。

(6)

s.t.

(7)

(8)

(9)

(10)

t=2,3,…,T；

(11)

(12)

t=2,3,…,T；

(13)

(14)

其中：约束(7)和约束(8)表示未开放的中转点不能参与产品的供应；约束(9)规定了必须满足需求点的产品需求；约束(10)和约束(11)为流量平衡约束，式(10)规定了第一阶段中转点无库存的情况下，产品的供出量应不超过供入量，式(11)规定了从第二阶段开始的每一阶段中转点有库存时，产品的供出量应不超过供入量与库存量之和；约束(12)和约束(13)为容量限制约束，式(12)规定了第一阶段中转点无库存情况下，产品的供入量不能超过最大容量，式(13)规定了存在库存的情况下，产品的供入量与库存量之和不能超过最大容量；约束(14)规定了决策变量的类型。

1.4 适应度函数计算

定义适应度函数由目标函数和惩罚项组成：

fi(x)=Ci(x)+M·P(x)。

(15)

式中：fi(x)表示第i个适应度函数，Ci(x)为模型的第i个目标函数，M为惩罚因子，P(x)为模型的约束违反度，x为个体向量。

定义模型的约束违反度如下：

(16)

对于不等式约束：cj(x)=max(0,gj(x))，gj(x)≤0为模型中第j个不等式约束；对于等式约束有：cj(x)=max(0,|hj(x)-ε|)，hj(x)=0为模型中第j个等式约束，ε为一个很小的实数。

为了保证寻优过程前期的全局探索能力，以及后期最优解的可行性，定义M为

(17)

式中：M0为较大的常数，itert表示第t阶段的迭代次数，max_itert表示第t阶段的最大迭代次数。可以看出，随着迭代次数的增加，惩罚力度逐渐加大。

1.5 编码方式

本文在进化算法的每个个体上采用实数和二进制混合编码的方式。结合产品供应动态优化模型，令x=(x1,x2,…,xD)为一个个体向量，则其编码方式如图1所示。其中，x1～xi×j+j×k为实数编码，xi×j+j×k+1～xi×j+j×k+j为二进制数编码。图1中的i、j和k为对应模型中供应点、中转点和需求点。

2 求解算法

2.1 算法框架及求解步骤

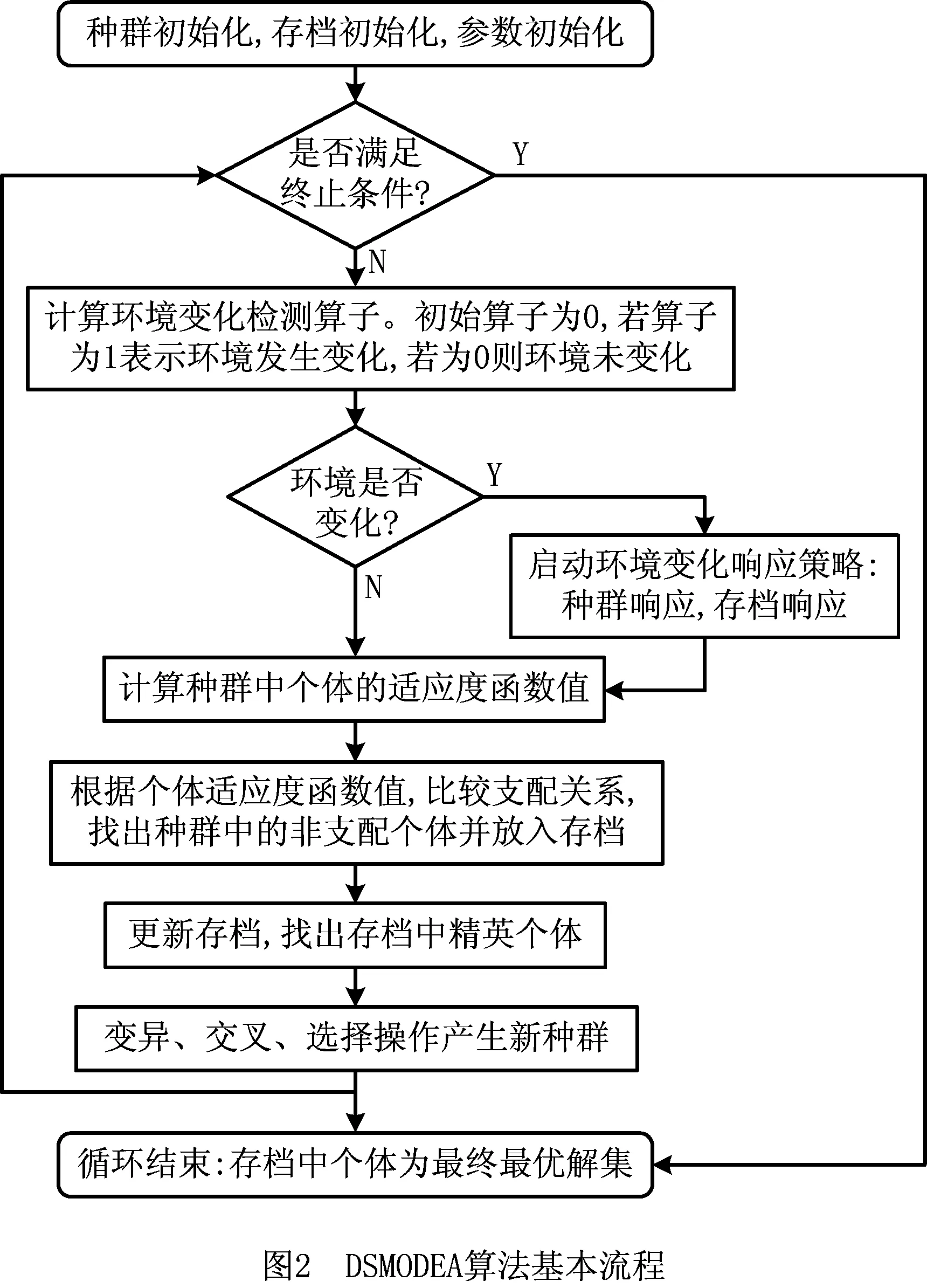
为求解所提出的动态多目标优化模型，本文对传统差分进化算法进行改进，提出了动态自适应多目标差分进化算法(Dynamic Self-adaptive Multi-objective Differential Evolutionary Algorithm, DSMODEA)。DSMODEA在静态差分算法的基础上增加了环境变化监测算子、环境变化响应策略，并采用了自适应策略。

DSMODEA算法流程如图2所示。

2.2 环境变化检测算子

本文设计了一种不依赖于决策变量的监测算子：

(19)

2.3 环境变化响应策略

当环境变化时，本文采用以下响应策略：

(1)种群的响应策略 当环境发生变化时，本文的DSMODEA算法分别采用随机初始化和继续使用上代种群两种策略，并利用算法对两种策略的结果进行对比分析。两种策略均存在一定的局限性。随机初始化种群，即将动态优化过程分解为多个静态优化过程，该策略完全舍弃上一环境的种群信息将不利于算法的快速收敛；由于上一环境下的种群是经过寻优后得到的具有很强的收敛性，若继承上一环境中的种群将其作为新环境的初始种群开始寻优，很容易使算法早熟陷入局部最优。

(2)存档的响应策略 当环境变化时，由于模型参数发生变化，原支配关系不再适用新的问题，存档中的个体必须全部随机初始化。

2.4 存档更新策略

(1)分别计算种群中所有个体的适应度函数值，根据其Pareto支配关系选出所有非支配解。将非支配解放入存档中。当得到下一代种群后，再将新的种群与上一代的存档进行混合并得到混合种群。根据支配关系，将混合种群的非支配解存入存档。

(2)对拥挤距离进行计算根据每个目标函数对种群中的所有个体按升序进行排序。第一个和最后一个个体的拥挤距离设为无穷大，第i个个体的拥挤距离则设为第i+1和第i个体的所有目标函数值之差的和。伪代码如下：

拥挤度距离伪代码

1. 初始化所有个体拥挤度距离:d(i)=0

2. For每个目标函数j=m

3. 根据第m个目标对每个个体进行排序

4. 令第一个和最后一个个体的拥挤度为正无穷大:d(1)=+,d(N)=+

5 for i=2:N-1

7. end for

8. end for

(3)选取存档中拥挤度最小的个体作为精英个体。

2.5 寻优过程

步骤1变异操作。

令xi=xi1,xi2,…,xiD为第i个父代个体向量，vi=vi1,vi2,…,viD为根据变异策略产生的变异个体向量。本文采用DE/current-to-best/1策略进行变异：

vi=xi+F×(xelite-xi)+F×(xrand-xi)。

(20)

式中：xi为父代个体，xelite为当前种群中的最优个体，xrand为从存档中随机选取的个体，且xi≠xelite≠

xrand，F是变异率。DE/current-to-best/1策略可以充分利用当前种群中精英个体的信息，从而保持较好的收敛性。

由于在算法迭代后期，较大的变异概率变异不利于个体向最优个体的收敛，因此本文设计了自适应变异概率，用来控制个体在不同进化代数中的变异概率。

(21)

式中，F0∈[0,1]为初始变异概率，max_itert表示第t阶段的最大迭代次数，itert表示算法在第t阶段的当前迭代次数，iter为整个算法的当前迭代次数。

步骤2交叉操作。

交叉个体向量ui由父代个体xi和变异个体向量vi经如下交叉操作产生：

(22)

其中：randij为[0,1]之间均匀分布的随机数，CR∈[0,1]为交叉率，即当变异个体vi上第j个变量vij对应的随机数小于交叉率时，该变量取父代个体对应值xij，否则保留变异个体上的值。可以看出，CR的值设置的越大则，进行交叉操作的概率越大。

步骤3选择操作。

根据种群中的父代个体和交叉个体的适应度函数，一一比较其支配关系。若某父代个体被对应的交叉个体支配，则用该交叉个体替换对应父代个体。最终得到的个体构成选择个体种群，作为子代个体进入下一次迭代。

3 算例分析

3.1 算例及实验设置

某物流网络由2个供应点，4个中转点和6个需求点组成。产品供应任务分5个阶段完成，不同阶段需求点的产品需求、缺件损失以及各运输费用各不相同，具体相关信息如表1～表5所示。

表1 节点间单位产品运输成本 百元

续表1

注：每一栏数据从左至右分别为第一阶段到第五阶段的运输成本。

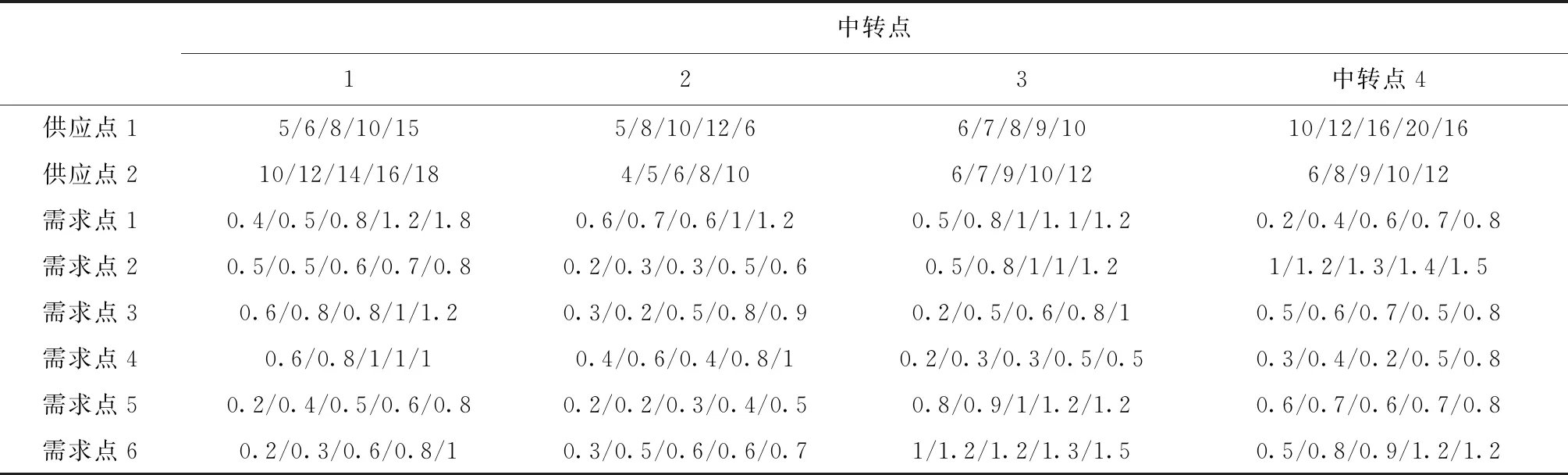
表2 节点间单位产品运输时间 h

注：每一栏数据从左至右分别为第一阶段到第五阶段的延迟时间。

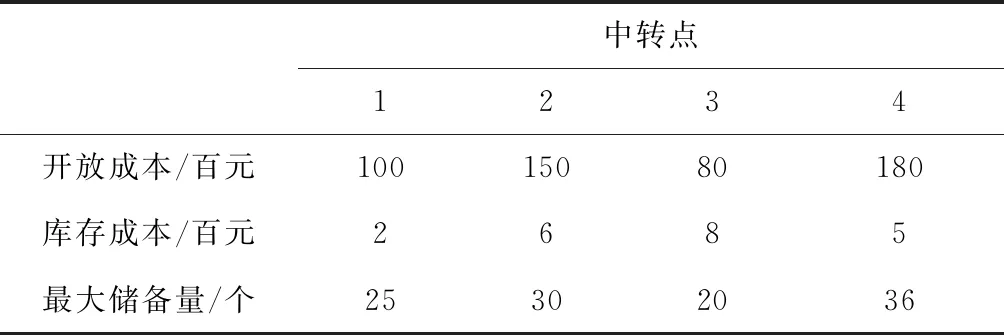
表3 中转点相关信息

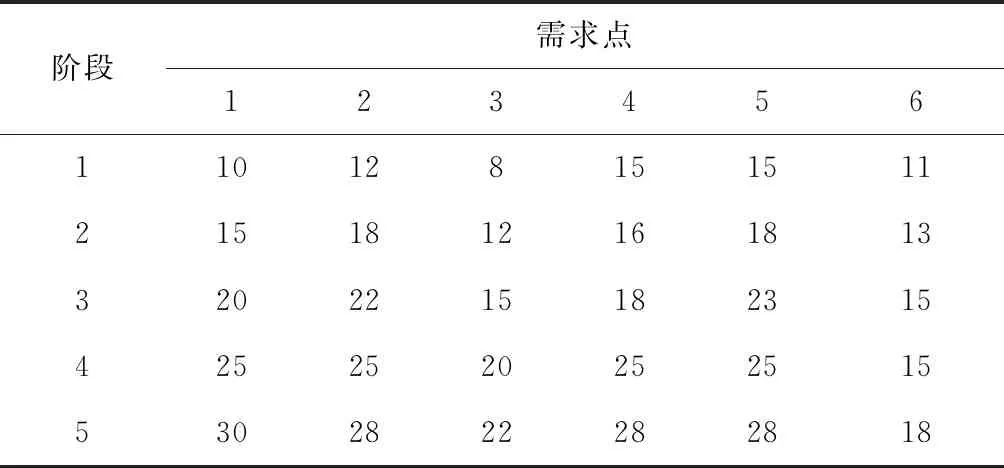
表4 需求点单位产品缺件损失 百元

表5 需求点在各级段的产品需求量 个

3.2 计算结果

利用DSMODEA对模型进行求解，得到每一阶段的最优供应方案。由于篇幅问题，无法展示所有阶段求得的全部供应方案，本文仅以一种优化结果对供应方案进行说明，表6给出了一个供应方案的示例，结合DSMODEA算法的编码方式可以获得中转点的开放情况以及产品在节点之间的供应数量。结果分析，主要针对各方案对应的适应度函数和目标函数进行对比分析。

表6 模型第三阶段供应方案

续表6

因此x1～x4依次为供应点1向4个中转点的产品供应量，x5～x8依次为供应点2向4个中转点的产品供应量；x9～x14、x15～x20、x21～x26、x27～x32分别为4个中转点向6个需求点的产品供应量；x33～x36表示4个中转点的开放情况，1表示开放、0表示关闭，则该方案下4个中转点全部开放。

图3是每个阶段求得的最优解在目标空间上的分布。第一阶段得到1个最优解，第二阶段求得9个最优解，第三阶段求得4个最优解，第四和第五阶段均求得1个最优解。可以看出每个阶段中的最优解集是互不支配的。

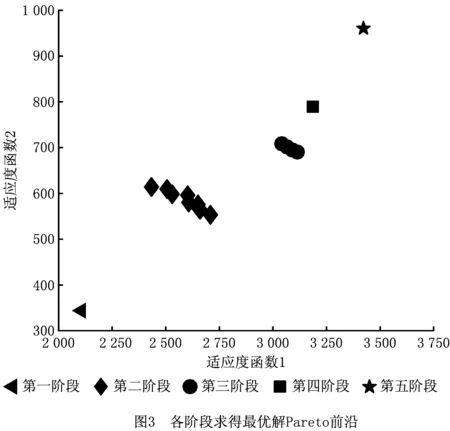
表7给出了每个最优解的适应度函数和目标函数值。从表7可以看出，所有最优解的适应度函数与对应的目标函数是相等的，由1.4节适应度函数表达式可知所有最优解对应的约束值均为零，即所有的解均为可行解。同时，对比最优解的两个适应度函数值，验证了各阶段最优解互不支配。

表7 DSMODEA算法求解结果

3.3 灵敏度分析

为了研究优化环境发生变化(供应阶段发生变化)时对算法的影响，分别比较以下两种种群环境变化响应策略的精英个体的适应度函数收敛情况。结果分别如图4a和图4b所示。图4a为环境变化后，采取随机初始化种群的结果，记为策略1；图4b为环境变化后，继续继承上代种群进入下一环境进行寻优的结果，记为策略2。可以看出，两个适应度函数的变化规律是相同的，且环境变化时继承上代种群的波动要远远小于随机初始化。这是由于新的种群利用了上代种群中的信息，可以快速的收敛。因此，DSMODEA采用继承上代种群的环境变化响应策略。

响应策略2下的算法相当于将动态优化问题分解为多个单阶段静态优化问题，再分别进行优化。从图4中可以看出静态优化需要分别对每一阶段进行初始化并重新寻优，计算成本太大。而动态优化利用了前一阶段的信息，在环境发生变化时波动较小，且能够快速收敛。由于响应策略2主要是对每次环境变化时的初始种群进行了优化，用继承上代种群代替随机初始化，这个过程没有增加计算量，并未改变算法的框架，因此不会对算法的复杂度造成影响。该策略的优势在于经过优化后的初始种群更加接近于最优解集，从而可以加快寻优进程。动态优化算法的整体优化代价要远小于静态优化算法，且随着阶段数的增加，该优势体现的越明显。

为了验证本文提出的自适应飞行策略在求解动态多目标优化问题时的效果，分别在不采用莱维飞行策略和以全概率进行莱维飞行时对本文的模型进行求解，将其结果与DSMODEA的结果进行对比。表8给出了不采取莱维飞行策略时的求解结果。从表中可以看出，所求结果的适应度函数值远大于目标值，即约束违反度很大，为不可行解。另一方面，表8中各最优解的成本和时间均远大于表7所得结果。这是由于未采取莱维飞行时，种群的多样性较差，算法很容易陷入局部最优。表9是以全概率进行莱维飞行时的结果，各阶段结果同样为不可行解，但约束违反度相对较小。同时，所花费的成本和时间也均大于表7结果。这是由于全概率莱维飞行时，算法在后期不利于收敛。

表8 未采取莱维飞行时的求解结果

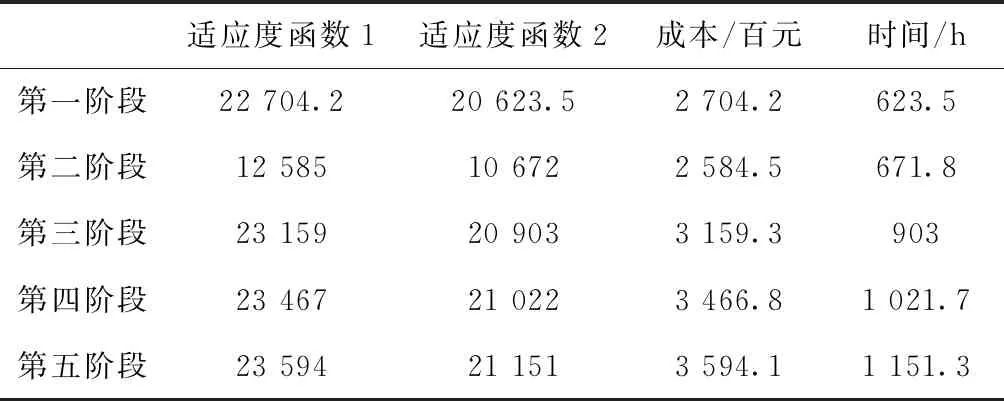
表9 全概率莱维飞行时的求解结果

4 结束语

本文构建了多阶段物流网络优化模型，将实际问题转化为多目标数学优化模型。为解决动态优化问题，提出了一种智能优化算法。在静态优化算法的基础上，使得差分进化算法可以用来解决动态优化问题。采用了自适应变异策略，解决了动态优化问题中当优化环境发生变化时算法收敛性与分布性发生冲突的问题，大大提升了算法的性能。通过算例，得到了模型的非支配解集，同时通过对比分析，验证了算法的有效性和效率。本文建立了物流网络动态优化的基本框架，提供了一种不依赖于问题本身的元启发式智能优化算法，为实际物流网络产品供应提供了思路和参考。未来，将进一步以基于多种群的并行动态优化算法和基于数据驱动的动态优化算法为重点，继续开展物流网络动态优化的相关研究。