基于红外无损检测的非金属材料粘贴缺陷识别

（武汉理工大学 安全与应急管理学院，湖北 武汉 430070）

0 引言

非金属材料的粘贴结构在工业生产、航空航天、军事、建筑等领域具有广泛的应用性和诸多的优越性[1]，但是粘贴界面容易出现脱粘、分层、夹杂等缺陷，进而降低系统的保温隔热性、耐久性和防火安全性，最终引发安全问题。因此，对非金属材料的粘贴缺陷进行无损检测具有重要意义。

近些年来应用广泛的红外无损技术与其他常规无损检测方法相比，具有适用范围广、非接触性、测温范围广、结果直观可靠等[2]优势。目前许多学者基于红外无损检测技术，对材料内部的缺陷进行探测，对其进行定性定量分析，同时提出各种算法以实现缺陷的可视化。在缺陷的定性定量方面，M.Barus[3]等通过对复合材料内部粘贴缺陷试样表面温度场的处理，验证了红外无损检测技术对检测复合材料脱粘缺陷的可行性；刘俊岩[4]等建立热波在试件中传导的热-电等效模型，得到了缺陷深度和反射热波与入射热波相位差之间的关系，获得缺陷大小及位置信息；王黎明[5]等运用红外热图和温差-时间对数曲线两种方式识别缺陷，缺陷识别精度达到0.4 mm；Balageas[6]和Holtmnn[7]等分别总结了脉冲法和锁相法在缺陷厚度、类型、导热率等定性定量分析的应用。在缺陷识别及提取方面，汪子君[8]等通过改进OSTU算法搜索最佳阈值实现红外图像的缺陷分割；梅林[9]等提出基于遗传算法优化求解的红外无损检测缺陷信息新方法；王涛等[10]人将粒子群优化算法和二维最小误差分割算法相结合，能够在实现更低对比度的红外图像分割；范春利[11-12]等使用共轭梯度法都缺陷边界进行定量识别，数值算例证明了该算法的有效性；此外，还有学者基于BP 神经网络[13]、小波变换[14]等识别并提取缺陷。缺陷的识别技术虽然已经取得了宝贵成果，但由于实验环境、技术制约等问题，在实际工程应用中仍然无法进行精确的缺陷定量识别。

本文研究了持续激励条件下非金属材料粘贴缺陷的边界特征，确定了对粘贴缺陷边界进行定量分析的方法。根据边界特征结合了Canny 边缘检测算法，改进了算法的识别结果，最终对粘贴缺陷边界几何特征进行识别，并标识出缺陷区域。实现对非金属材料粘贴缺陷的定量检测并将缺陷可视化，可为红外无损检测的工程应用提供理论基础和技术指导。

1 粘贴缺陷边界特征研究

目前红外无损检测技术根据激励方式不同，主要分为脉冲激励红外无损技术、锁相激励红外无损技术和持续激励红外无损技术。其中，持续热激励方式相较于其他热激励方式，更适合热导系数较低且厚度较大的非金属材料[15]。本文采用持续热激励法研究粘贴缺陷，使用CFD 流体分析软件研究在二维条件下的缺陷边界特征，并提出缺陷边界识别方法，最后在三维条件下验证方法的可靠性。

1.1 二维数值模拟

假设防腐材料片状的粘贴缺陷是由粘贴时胶水中含有气泡导致，则防腐材料表面在激励辐射热流作用下温度上升，而缺陷部位（空气）的热扩散系数要远小于胶水，导致该部分热量扩散较无缺陷部位缓慢，因此该部位对应的表面温度比周围温度较高。本文为研究非金属材料粘贴缺陷边界的温度分布特征，使用CFD 流体分析软件，假设基体材料为铁，非金属材料为PE，两者之间使用胶水粘贴，胶水的厚度处处相等，气泡假设由空气填满且位于试样的中心，气泡的大小和高度即为缺陷的大小和程度。试件二维模型及边界传热条件如图1所示。4种材料的密度、导热系数、热容[16]如表1所示。通过数值模拟计算，图2给出稳定状态时不同缺陷半径R下，表面温度及温度梯度的分布曲线，其中r表示试件上表面各点与对称轴的距离，T表示对应点的温度，dT/dr表示对应点的温度梯度。

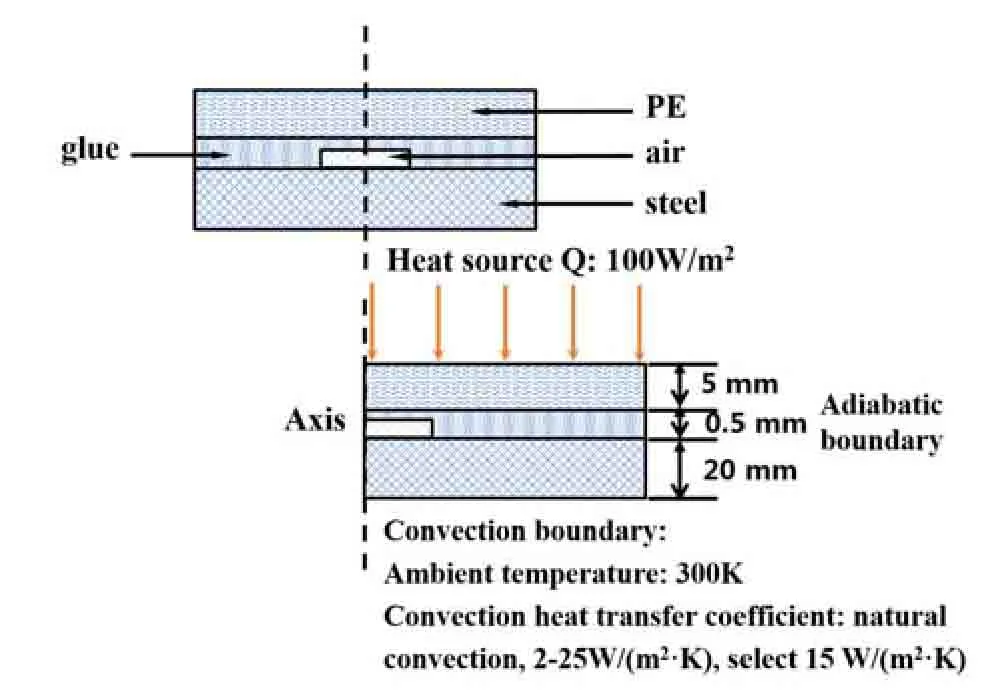
图1 粘贴缺陷二维轴对称模型示意图Fig.1 The diagram of two-dimensional axisymmetric model of paste defect

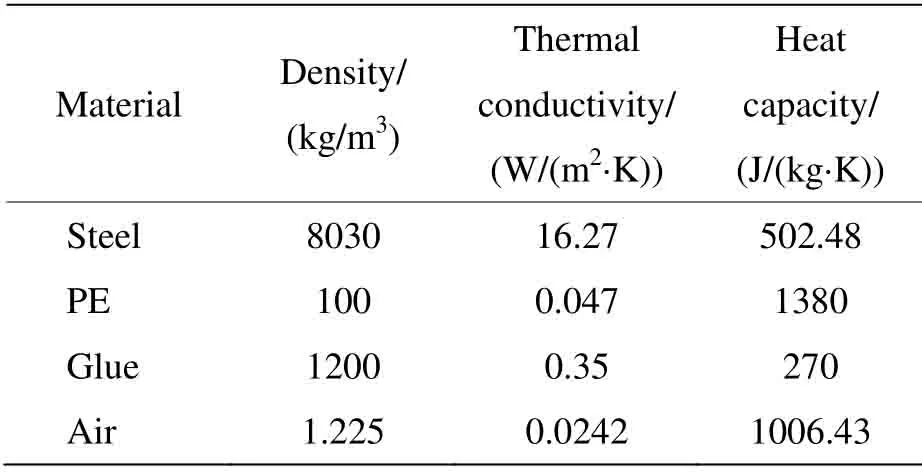
表1 材料热物性参数Table1 Material thermal property parameters

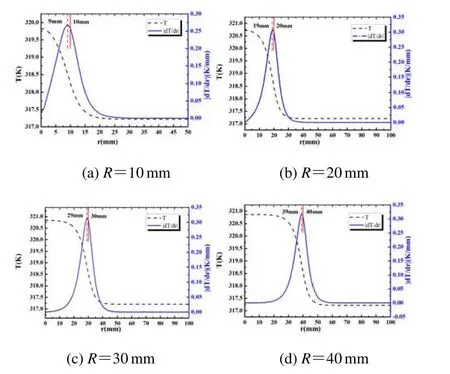
图2 二维模型的表面温度及温度梯度分布曲线Fig.2 Surface temperature and temperature gradient distribution curves of two-dimensional models

从不同缺陷半径对应的温度分布曲线可以看出，缺陷区域呈现高温状态，缺陷边界处的温度快速下降。根据表2缺陷边界的温度可得知，随着缺陷半径的增加，缺陷边界对应的表面温度也随之升高，这是由于缺陷半径越大，缺陷区域内积累热量越多，试件表面温度越高[17]。此外，粘贴材料的不同也会影响试件表面温度[18]。因此，无法利用温度值作为阈值检测出缺陷边界的准确位置，需要找到更普遍的规律来识别缺陷边界。

在粘贴缺陷的边界处，由于空气的热扩散系数远远小于胶水的热扩散系数，因此热量由空气传向胶水。根据导热的傅里叶定律，在缺陷的边界热流密度将达到峰值。因此，可考虑通过计算温度梯度峰值位置来确定缺陷边界。由温度梯度分布曲线可以看出，温度梯度在缺陷边界位置附近达到极值。表2给出了通过温度梯度极值确定的计算缺陷半径与实际缺陷半径对比，结果显示两者的相对误差较小，因此验证了使用温度梯度极值确定缺陷边界的可行性。

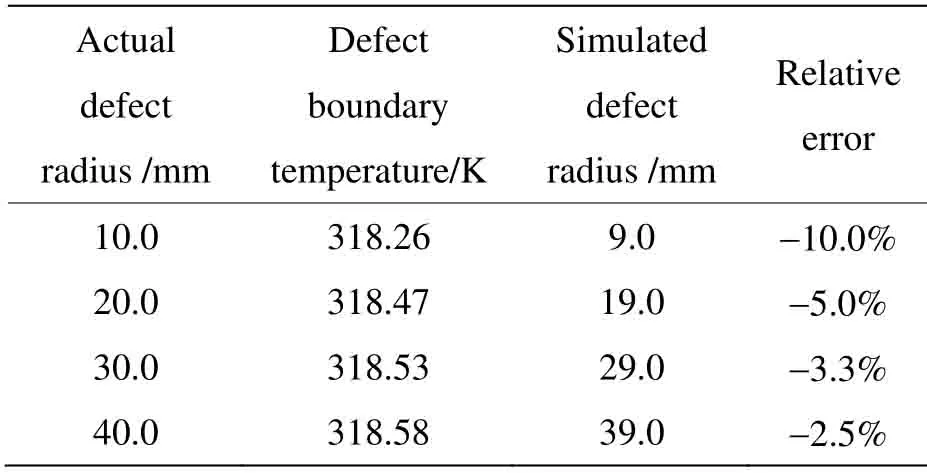
表2 计算缺陷半径与实际缺陷半径的对比Table2 Comparison of simulated defect radius with actualdefect radius

1.2 缺陷边界识别算法

根据温度梯度在缺陷边界处达到极值这一特性，准确地筛选出温度梯度极值部位即可识别边界位置。由于Canny边缘检测算法的原理是计算像素的梯度大小及方向后采用非极大值抑制和双阈值来去除误检点及保留漏检点[19]，这与筛选出温度梯度极值来确定缺陷边界的过程一致，因此考虑采用Canny 边缘检测算法对试件表面温度分布进行缺陷识别。

为验证使用Canny边缘检测算法可筛选出温度梯度极值的可靠性，本文首先利用CFD 流体分析软件，使用三维模型进行验证。建立含有底面为圆形及正方形形状缺陷的三维模型，如图3(a)所示试件三维模型。两种类型缺陷的底面尺寸如图3(b)所示，圆形直径Φ为40 mm，正方形边长L为30 mm。使用CFD 流体分析软件，其边界条件及试件材料与二维模型一致，得到如图4所示的试件表面温度分布云图，结果显示在缺陷对应的上表面存在局部的高温区域，但无法准确定位缺陷边界的位置。

对其进行一阶微分处理得到如图5所示的表面温度梯度分布等高线图。由温度梯度等高线图可知，缺陷区域形成“火山”状地形，在缺陷边界处形成“山脊”，即温度梯度在缺陷边界处达到极值。对两种缺陷的温度分布数据使用Canny算法进行检测，得到如图6所示的缺陷边界点集合。使用Canny算法得到的缺陷边界所围成的区域面积与实际缺陷面积进行对比，如表3所示。结果显示Canny 边缘检测法检测出的缺陷边界所围成的区域面积与实际缺陷区域面积基本吻合。

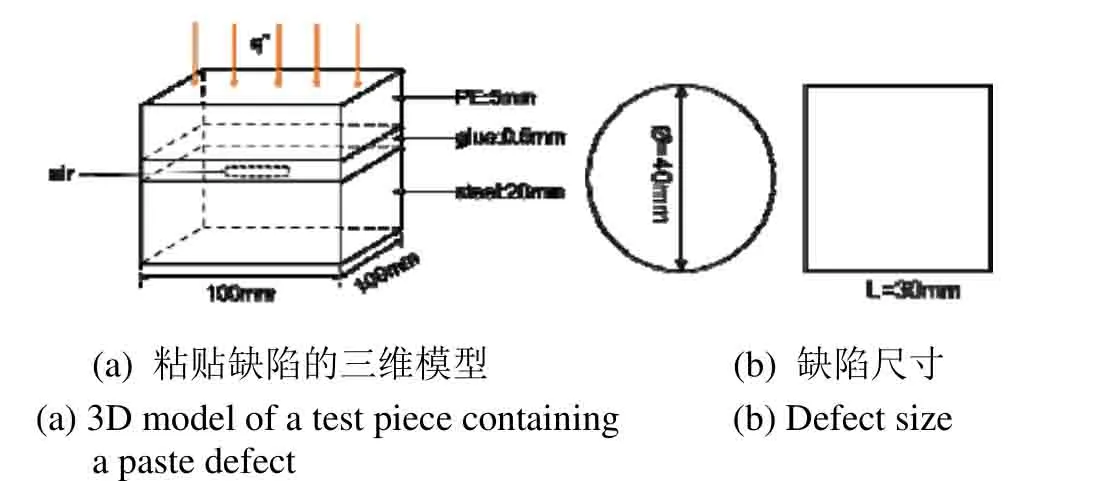
图3 三维模型试件及其缺陷尺寸Fig.3 3D model test piece and its defect size

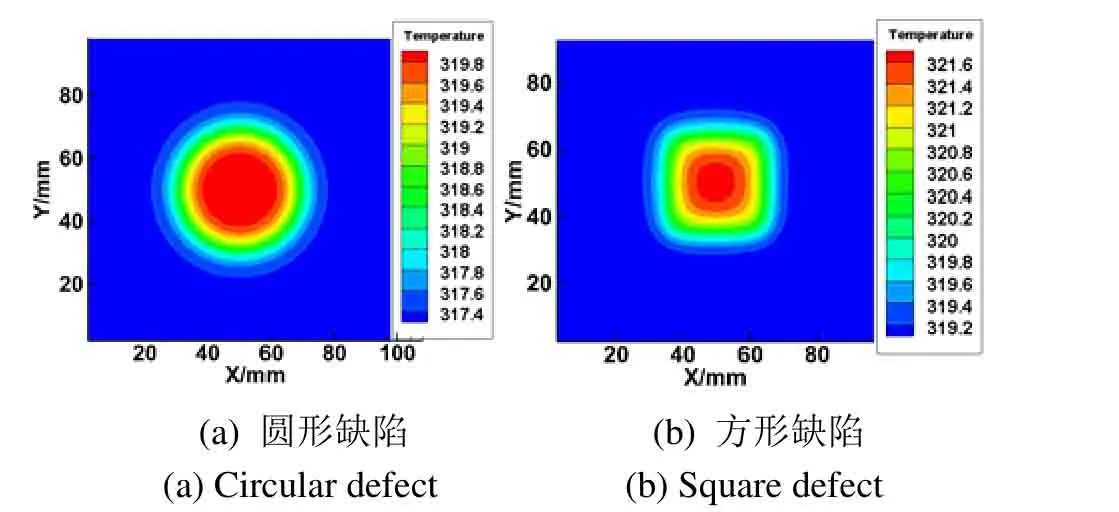
图4 三维模型的表面温度分布云图Fig.4 Surface temperature distribution of a three-dimensional model

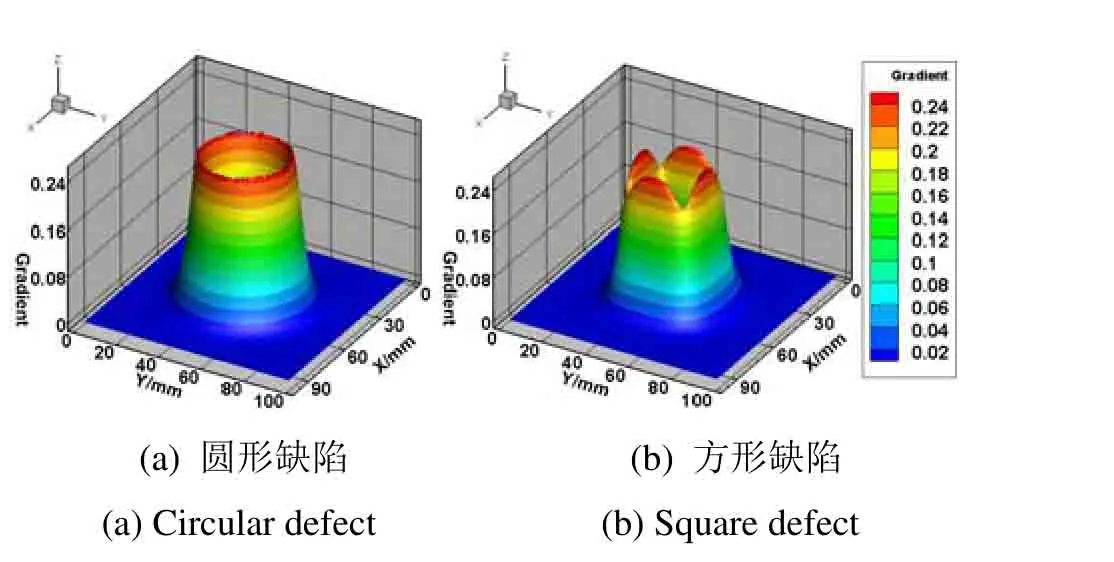
图5 三维模型的温度梯度分布等高线图Fig.5 Contour map of temperature gradient distribution of 3D model

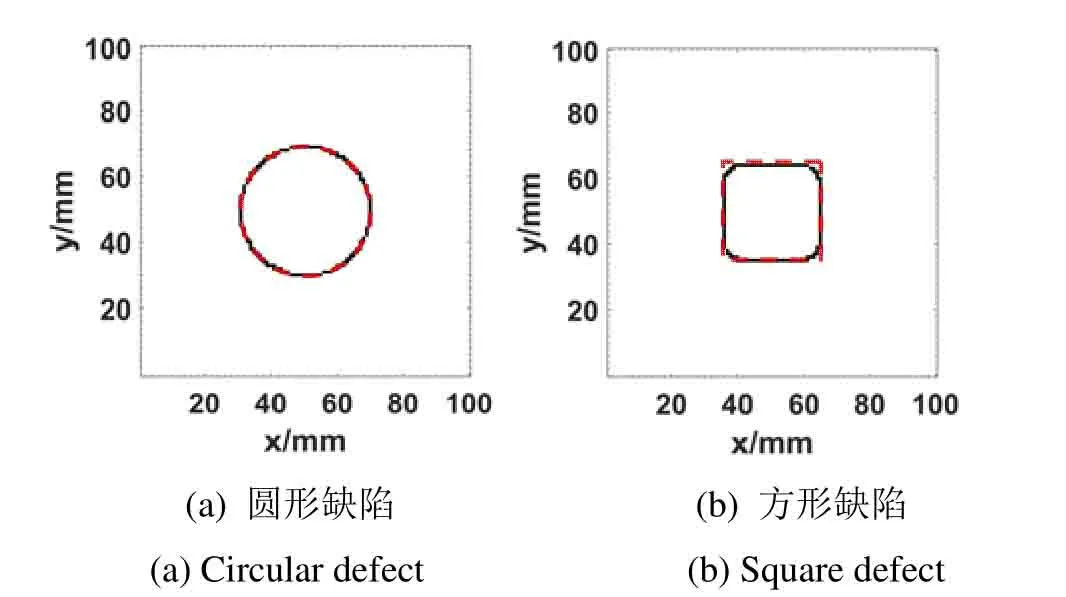
图6 基于Canny算法的缺陷识别结果Fig.6 Defect identification result based on Canny algorithm

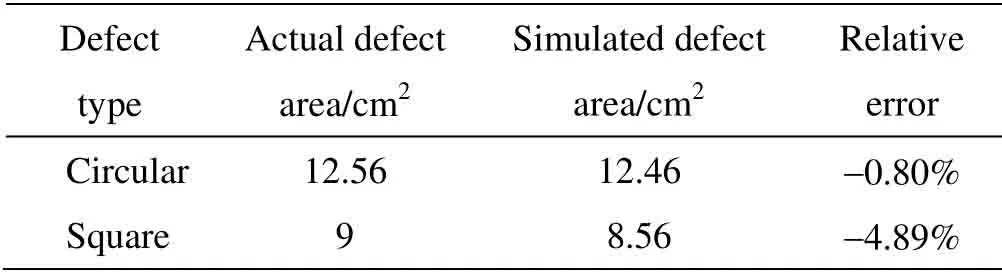
表3 计算缺陷面积与实际缺陷面积的对比Table3 Comparison of simulated defect area with actual defect area

2 粘贴缺陷识别实验验证

2.1 实验装置

实验平台示意图如图7所示，红外热像仪采用Fotric 688，光源由6 根长为40 cm的红外管式碳纤维灯管组成。为验证前文模拟得到的缺陷边界定量方法可靠性，制备如图8所示的含有4种尺寸脱粘缺陷的试样。为避免光源直接照射试样产生较强的反射，影响实验结果，将试样倾斜30°，即入射光源与试样法线夹角为30°进行实验。

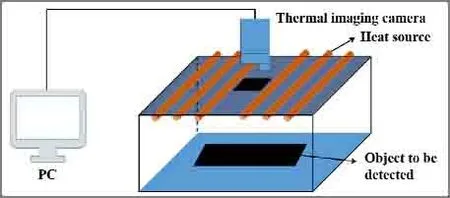
图7 实验平台示意图Fig.7 The diagram of the experimental platform

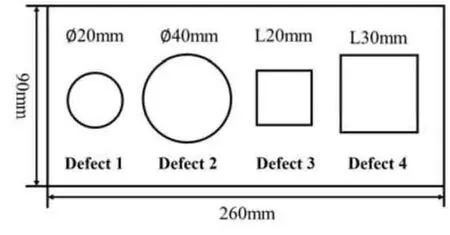
图8 含脱粘缺陷试样平面示意图Fig.8 The diagram of a sample containing debonding defects

2.2 实验结果分析

试样在持续热激励150 s 后得到如图9所示的红外热图，结果显示试件表面红外图具有4个明显的高温区域，但因受热不均、周围环境噪声等影响，所采集到的数据存在噪声较大、边缘模糊等问题。

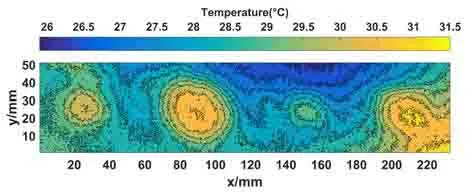
图9 实验试件表面温度分布云图Fig.9 Contour map of surface temperature distribution of experimental specimens

对试件表面温度分布数据使用高斯滤波进行降噪处理后得到如图10所示的表面温度分布图。根据前文得到使用温度梯度极值来确定缺陷边界的定量分析方法，对试件表面红外测温数据进行一阶微分处理得到相应的温度梯度分布，如图11所示，采用Canny 边缘检测算法对试样4 块缺陷区域进行定量识别，其结果如图12所示。

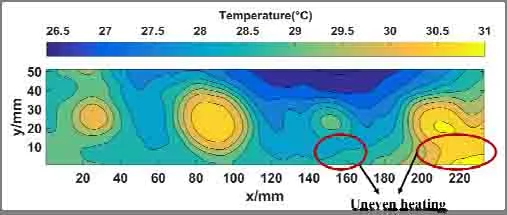
图10 降噪处理后的试样表面温度云图Fig.10 Contour map of the surface temperature of the sample after noise reduction treatment

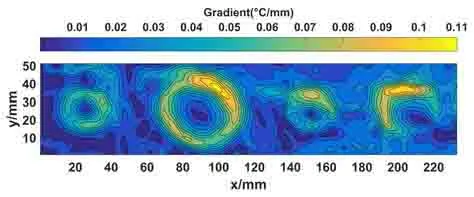
图11 试样的表面温度梯度分布等高线图Fig.11 Contour map of surface temperature gradient of sample

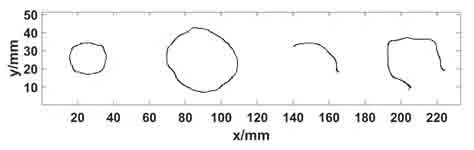
图12 基于Canny算法的试样缺陷识别结果Fig.12 Identification result of sample defects based on Canny algorithm

结果显示使用Canny边缘检测算法识别的缺陷边界与实际缺陷边界相比存在明显的误差，第一个和第二个缺陷的检测结果为完整、闭合的边界，但第三个和第四个缺陷边界只能检测到部分边界。这是由于缺陷3和缺陷4 受热不均匀，造成缺陷边界处有局部高温，使检测到缺陷部分边界模糊，如图11 中标识出的部分。而Canny 边缘检测算法采用双阈值法，从而漏检了缺陷3和缺陷4 部分边界模糊的“弱边界”，即温度梯度较小的部分，导致检测到的缺陷3、4 不完整。

由以上分析可知，Canny 边缘检测法在数值模拟理想条件下可识别出准确的缺陷边界，但在实验条件不理想时存在误差，需要进一步改进算法得到较为理想的识别效果。

2.3 改进的缺陷边界识别及标识算法

根据前文的数值模拟结果可知温度梯度在缺陷边界达到极值，因此缺陷边界处的像素点的温度梯度值总会比领域至少一个方向的像素值大。利用这一结论，可设计算法筛选出所有“疑似边界点”集合，具体思路为：将目标像素点Pi,j与其领域水平、垂直、斜45°四个方向上的像素点相比较，若目标像素点的温度梯度值大于任一方向上的两个像素点的温度梯度值，则认为该点为“疑似边界点”。

对红外无损实验得到的试件表面温度梯度分布数据进行该方法的筛选后得到如图13所示的“疑似边界点”集合。从结果可知，疑似边界点集合内包括了4个完整的闭合缺陷，且该形状与大小与实际缺陷基本吻合。因此，利用疑似边界点集合可对Canny算法识别的缺陷边界进行补充，从而得到完整、闭合的缺陷边界。利用“质心填充”法，从每个缺陷的质心位置开始填充，当遇到边界时停止填充，得到最终识别到的4个缺陷区域，如图14所示。

图13 疑似边界点集合Fig.13 Collection of points suspected of being borders

在计算缺陷面积时考虑了试样与入射光源存在一定的夹角，计算得到算法检测的缺陷面积与实际缺陷面积，如表4所示。

根据计算结果可以看出，检测缺陷面积与实际面积相比存在一定的误差，缺陷1、2 存在较小误差，但缺陷3、4 误差明显偏大，这可能是由于缺陷3、4表面受热不均匀，局部温度偏高从而产生的误差；另外一方面，由于缺陷3、4 为正方形，其4个尖角部位因热扩散导致其对应的温度分布呈现圆滑的形状，导致检测到缺陷3、4的面积有部分损失。

图14 改进Canny算法得到的缺陷识别结果Fig.14 Identification result of defects obtained by improved Canny algorithm

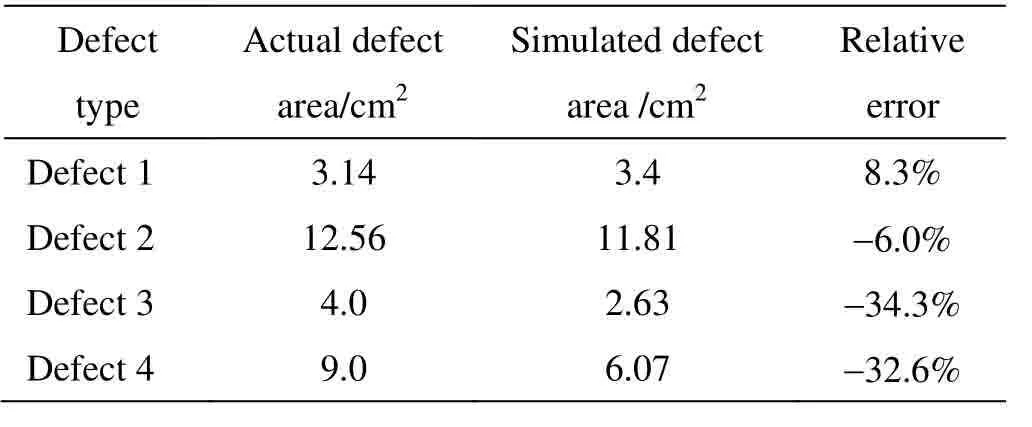
表4 算法检测的缺陷面积与实际缺陷面积对比Table4 Comparison of defect area detected by algorithm and actual defect area

3 结论

本文基于红外无损检测技术，在持续激励条件下对粘贴缺陷试件进行数值模拟和实验验证，研究了温度梯度分布与缺陷边界的关系，并设计了粘贴缺陷的定量识别算法。主要结论如下：

1）通过建立二维及三维粘贴缺陷模型，在持续激励条件下得到模型对应的上表面温度分布及温度梯度分布，温度梯度在缺陷边界处达到极值；

2）由于实验得到红外热图存在部分边界模糊、噪声较大等问题，对Canny算法进行改进后，可补充其缺损的缺陷边界，得到完整、闭合的缺陷边界。