皮之不存 毛将焉附——对复习课《一次函数图像画法》的感悟

■甘肃省张掖市高台县城关初级中学 叶建生

一、三种画法的综合阐述

（一）多点法画一次函数图像

采用多点法画一次函数图像是学习一次函数图像的基础,尽管比较烦琐，但对于初学函数图像的学习而言意义重大。其真正作用有四点：一是学生能通过多点法画图感悟到一次函数图像的详细形成过程，利于学生对函数性质的理解；二是学生能掌握画函数图像的基本方法（列表、描点、连线），为今后反比例函数图像学习和二次函数图像学习做铺垫；三是学生通过细致的作图过程，能够形象化地观察到函数图像上点的横、纵坐标的变化情况，深刻理解函数图像的实质；四是学生通过对不同k、b 值的一次函数作图，理解y=kx+b(k≠0,k、b 为常数)中k、b 两个元素对于函数图像的影响。

（二）两点法画一次函数图像

两点法画一次函数的图像的理论依据是“两点确定一条直线”。从这个层面讲，我们可以提前让学生模糊地体会到代数知识与几何知识的联系（一次函数在高中阶段归类到解析几何的范畴），这种影响是潜在的，便于学生构建数学知识体系，对于帮助学生树立大数学观理念具有深远的意义。就两点法画一次函数图像而言，究竟如何选取两个点才最优化？任意选还是找关键点？这就要求我们引导学生积极探究、深入讨论，最终归纳、提炼出有效方案。课堂教学实践证明，大部分学生能迅速有效选取图像与x轴和y轴的交点为最佳点。因为与x轴的交点，点的纵坐标为0，与y轴的交点，点的横坐标为0。

（三）简易法画一次函数图像

简易法画一次函数图像，其主要体现的数学思维是逆向思维。也就是说，在学生充分掌握y=kx+b(k≠0,k、b 为常数)中k、b 两个元素意义的前提下，简洁、快速地画出一次函数的草图，有利于学生解决实际数学问题。在平时的练习题或综合测试题中，往往需要我们画出一次函数草图来解决问题，而没必要画出精确图形。从另一个侧面看，学生能否快速根据一次函数表达式确定出图像所经过的象限，也是检验学生是否掌握好本知识点的一个重要标准。

二、三种画法的实际解题价值

（一）三种画法的关系

多点法、两点法、简易法三种画图方法之间存在紧密的内在联系，犹如新课标中提到的知识、能力和技能三者的关系一样。多点法是画图基础；两点法是画图能力提升；简易法则是画图技能展现。这三种画法，由简单向难自然过渡，体现了知识的层层递进性，这从根本上也符合初中学生的数学认知习惯。

（二）三种画法在解题过程中的实效价值

从整个初中数学教材编排顺序来看，一次函数的学习放到了初中函数类知识学习的最前面，这符合学生的思维习惯。因为，一次函数图像的画法可为其他类函数图像的画法提供参考，能对学生在学习其他函数图像时起到触类旁通的作用。

单就本节课一次函数图像的三种画法来看，多点法是精确画法，要求学生能够熟练掌握。学生掌握好它的现实意义在于能够直观地感受到直线上点的横纵坐标的变化，同时也能感受到一次函数表达式中k 值对于图像的影响。即：k 的值关系到直线的倾斜程度（也就是高中知识所谈到的斜率）。当然，对初中学生，我们不直接说出斜率这个概念，我们仅要求学生了解一下。譬如在给学生解释k的意义时，我采取两种解释方法，一种方法是k＞0，图像必经过一、三象限，k＜0,图像必经过二、四象限。第二种方法是k＞0，直线与x轴正方向的交角是锐角，k＜0，直线与x轴的交角是钝角。这样解释的好处在于便于学生理解和掌握，同时也为高中知识中直线斜率的提出埋下了伏笔。如下图：

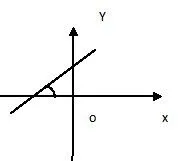
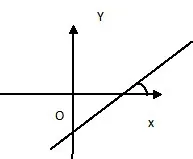
（k＞0时，直线必经过一、三象限）

（k＞0时，直线与x轴正方向的交角是锐角）

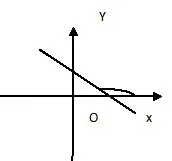
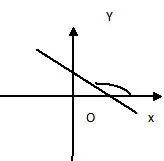
（k＜0，直线必经过二、四象限）

（k＞0时，直线与x轴正方向的交角是钝角）

两点法在学生解决实际数学题目中应用较广，掌握它的意义在于既不像多点法作图那样烦琐，又不像简易法作图那样随意，介于两者之间。它能使复杂的问题简单化，简单的问题具体化。尤其是直线与x轴和y轴的两个交点，更能体现两点法画一次函数图像的精髓。两点已确定，直线位置随之确定，直线与两坐标轴围成的三角形也随之确定，可谓一箭双雕。其实，在解决一次函数简单题目或综合性题目的过程中，我们发现应用最多的还是简易法画一次函数的草图。画函数图像的草图最直接的感受就是有效提高解题速度。当然，前提是学生必须真正掌握一次函数表达式中k、b的意义。简易法作图是一次函数作图学习中的神来之笔，即考查了学生掌握一次函数基本知识的程度，又考查了学生应用知识解决问题的能力。

三、三种画法的教学感悟

（一）更加清醒地认识到本节课在本章中的地位

一次函数图像画法的复习课结束后，我进一步体会到本节课在本章知识学习中的重要作用,因为只有掌握了函数图像的画法,学生才能够深刻理解函数的性质,从而为一次函数更高层次的学习夯实基础。如：一次函数与二元一次方程的关系；一次函数与一元一次不等式的关系；一次函数与反比例函数、二次函数的综合题的解答等，都特别强调两点法和简易法画一次函数图像的重要性。

（二）我的教学设计感悟

我在设计本节课时，仔细研究了新课标，认为本节的重点是：一是通过列表、描点、连线教会学生用多点法画一次函数的图像，并与学生一起总结一次函数图像的相关性质。二是让学生理解图像上的点的坐标与函数表达式之间的关系。三是引导学生熟练掌握用两点法和简易法画一次函数图像。

教学环节设计，我分为五步：

1.通过学生阅读课本，初步理解函数图像的画法，并通过举例让学生了解学习函数图像画法的重要作用。

2.通过实例向学生展示如何精确画一个一次函数的图像,并引导学生从中总结出利用多点法画函数图像的一般步骤。并先由学生归纳，后由教师总结出画函数的三个步骤:列表、描点、连线。

3.让学生独立完成例题画图，并从中发现学生在画图过程中可能存在的问题，做个别指导，并抽出典型问题进行讲解。

4.通过课件展示，一步步和学生共同探讨画一次函数图像的另外两种方法（两点法和简易法）。

5.升华提高，利用课件很直观地展示不同一次函数的图像，进一步帮助学生了解一次函数中k、b两个元素对图像的影响。

四、结语

在教学过程中，每节课总会有一些不尽如人意的地方。所以，如何有效调动他们的学习参与积极性是我今后备课过程中要多思考的地方。此外，由于本节课设计量大，我讲得太多，学生课堂练习相对较少，学生自主学习的时间和空间被抑制，以后要尽可能精选例题，由学生自己完成三种画法的知识体系建构。