关于运用程序性知识解题的几点注记

李 伟

(辽宁省鞍山市第三中学 114000)

教育心理学[2]将知识分为陈述性知识和程序性知识.程序性知识也叫操作性知识，直观理解这类知识主要用来回答“怎么做”的问题，特点是知识形成过程的程式化，即通过“顺序模块”和“顺序模块的组装”来形成.基于这些直观的理解和认识，试想探索的问题是，在涉及程序性知识问题解决时，可否呈现一些规律性的方法和手段，下面以导数部分中“曲线的切线方程”知识点为例加以说明阐述.

导数部分的“曲线的切点方程”是典型的程序性知识，具体形式为：曲线y=f(x)上一点M(x0,f(x0))处的切线方程y-f(x0)=f′(x0)(x-x0).对于这个知识点从知识形成过程可以分解为由以下几个“顺序模块知识”构成：顺序模块1.切点在y=f(x)的曲线上，即切点坐标满足曲线方程.顺序模块2.切线斜率k=f′(x0).顺序模块3.点斜式写切线方程.也就是说，关于“曲线切线方程”知识点可以分解为“三大顺序模块”，在求切线方程时，将每个模块任务完成后，按顺序“组装”起来即可.

上述对程序性知识理解的思考在解题中具有何种程度的指导意义，请看下面的示例.

示例1 (2019年全国理科数学3卷第6题) 已知曲线y=aex+xlnx在点(1,ae)处的切线方程为y=2x+b，则( ).

A.a=e,b=-1 B.a=e,b=1

C.a=e-1,b=1 D.a=e-1,b=-1

分析这是一道给出切线方程、切点、曲线方程，但含有参数的问题.对此，直接借助于上述给出的切线方程的“三大顺序模块”列出对应方程，即可求解.

略解由切线斜率等于切点导数值，得ae+1=2 ①；由切点在曲线上，得ae=ae+0(这是恒成立的等式，无用于本题的解决)；由切点在曲线上，得ae=2+b②.综合①②可得D.

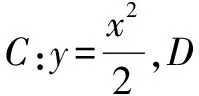
(1)证明：直线AB过定点；(2)略.

分析问题(1)是没有给出切点、切线斜率的切线问题.对此，借助于求曲线切线方程“三大顺序模块”的思想，通过设切点，求导求斜率，从而得到切线方程，再运用设“设而不求”[3]即可求解.

略解(1)设A(x1,y1)、B(x2,y2)，由于直线斜率kAD=f′(x1)=x1，所以，切线AD方程为y-y1=x1(x-x1)①.同理，切线BD方程为y-y2=x2(x-x2)②.

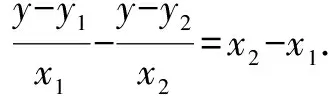
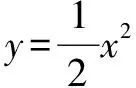
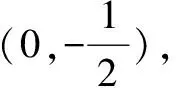
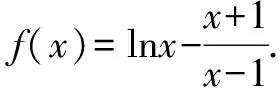
(1)讨论f(x)的单调性，并证明f(x)有且仅有两个零点；

(2)设x0是f(x)的一个零点，证明曲线y=lnx在点A(x0，lnx0)处的切线也是曲线y=ex的切线.

分析问题(1)略.

问题(2)是两条曲线的公切线问题.对此，同样借助于曲线切线方程分解为“三大顺序模块”的思想，通过设曲线y=lnx的切点A(x0，lnx0)，求导求斜率，从而得到切线方程，进一步，再推出该切线方程也是曲线y=ex的切线方程即可.

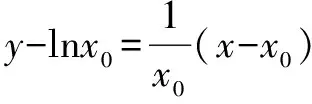
又曲线y=ex切于点B(x1,ex1)的切线方程为：y-ex1=ex1(x-x1)③.

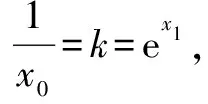
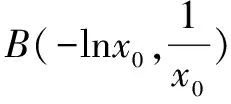
综合上述示例足以说明，采取将曲线切线方程(程序性知识)按其知识形成过程的逻辑顺序分解为若干“模块顺序知识”结构的思想去指导解题，全面地解决了各类曲线的切线问题，可见该想法的地位和作用的重要性.为读者更好把握，作为归纳总结,下面给出关于程序性知识解题做如下注记.

注记1 程序性知识的特点是知识形成过程具有“怎么做”的特点，即：要按知识形成过程即可做(求)出，具有很强的操作性.

注记2 对于程序性知识按只是形成过程的逻辑顺序进行分解，分解为若干“顺序模块”，这样便于应用解题时保证正确运用.

注记3 在解题运用时，敢于回归知识本身的基本结构(顺序模块)来思考，敢于运用“设而不求”的手段去思考问题的解决.

事实上，高中数学知识中程序性知识占有很大比重，如：等差数列、单调函数等都是程序性知识.高考中强调的重点考查“通性通法”，事实上也是针对程序性知识而言的.通过上述示例可以看出，在数学学习中如果能对其程序性知识，依据“三个注记”按其知识形成过程的逻辑顺序分解为若干“模块顺序知识”，并加以实际运用，一定对解题带来极大的帮助.