对一道高考题的研究

彭光焰

(湖北省广水市第一高级中学 432700)

2017年江苏省高考数学试卷21题D小题是：

题目已知a,b,c,d为实数，且a2+b2=4,c2+d2=16,证明：ac+bd≤8.

笔者参阅文献[1]、[2]、[3]，经过探索，得出不同于原试卷所提供的答案的九种不同证法.

一、拓展解法

分析1 比较法、综合法和分析法是证明不等式最基本最常用最重要的方法.本题的特点是字母较多、条件较多，因此用分析法、比较法和综合法来证明时，要注意变换的技巧和灵活处理已知条件.

证法1:综合法

因为a,b,c,d都是实数，所以

又因为a2+b2=4,c2+d2=16.

即ac+bd≤8.

证法2:比较法

证法3:分析法

当ac+bd≤0时，原不等式显然成立.

当ac+bd>0时，要证ac+bd≤8，只需证明(ac+bd)2≤64,

即只需证明a2c2+2abcd+b2d2≤64.①

由于a2+b2=4,c2+d2=16，因此①式等价于

a2c2+2abcd+b2d2≤(a2+b2)(c2+d2).②

将②式展开、化简，得(ac-bd)2≥0.③

因为a,b,c,d都是实数，所以③式成立，即①式成立，原命题得证.

分析2 观察已知条件和要证的结论，我们可以利用柯西不等式来证明此题，江苏省提供参考答案就是利用柯西不等式来证明的.

证法4:柯西不等式法

由柯西不等式可得：(ac+bd)2≤(a2+b2)(c2+d2).

因为a2+b2=4,c2+d2=16，所以(ac+bd)2≤64，因此ac+bd≤8.

分析3 受证法2的启发，我们可以得到恒等变形法.

证法5:恒等变形法

分析4 由题目已知条件a2+b2=4,c2+d2=16，我们可以联想到sin2α+cos2α=1，这启发我们用三角代换法来证明此不等式.

证法6:三角代换法

由已知条件我们可设a=2sinα,b=2cosα,c=4sinβ,d=4cosβ，则ac+bd=8sinαsinβ+8cosαcosβ=8(sinαsinβ+cosαcosβ)=8cos(α-β)≤8.所以ac+bd≤8.

分析5 平面向量是高中数学必修内容，在平面向量中有著名不等式，|a·b|≤|a||b|，这为我们证明不等式提供了一条途径.从该题的结构特点来看，我们易联想到|a·b|≤|a||b|.

证法7:向量法

证法8:几何法

分析7：利用复数的有关知识，我们也可以证明此不等式.

证法9:复数法

设z1=a+bi,z2=c+di,又|z1|+|z2|≥|z1+z2|，

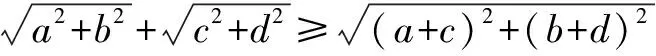
又因为a2+b2=4,c2+d2=16

分析8 普通高中课程标准实验教科书数学选修4-5A版不等式选讲介绍了二维形式的三角不等式，这又为我们解决此问题提供了一种方法.

证法10:二维形式的三角不等式法

由二维形式的三角不等式法可得

下同证法9.

我们又提供了九种证法，每一种证法所用的知识都是高中数学课本所包含的，教师在课堂上教学时对有些例题进行一题多解，课后教师要求学生对适宜一题多解的数学问题进行一题多解. 如何判断解题方法的合理性和科学性，主要根据题设和结论来判定，我们在选择解题方法时，要认真分析，辩证看待，全面考虑，科学决策.

二、拓展题目

著名科学家爱因斯坦说：“提出一个问题往往比解决一个问题更重要，解决问题也许仅是一个数学上或实验上的技能而已，而提出新的问题，新的可能性，从新的角度去看旧的问题，都需要有创造性的想像力.”因此，读书时，不仅要多动脑筋，勤于思考，不仅要懂得如何处理问题，解决问题，还要懂得如何发现新问题，提出新问题. 波利亚(G·Polya)说：“好问题同某种蘑菇有些相似，他们大都成堆的生长，找到一个以后，你应当在周围找找，很可能在附近就有几个.”我们对例习题进行一题多解的探究后，还应进一步思考，该题是否适合一题多变，通过探究，得出了下列新题.

新题1 已知a,b,c,d为实数，且a2+b2=4,c2+d2=16，证明ac+bd≥-8.

新题2 已知a,b,c,d为实数，且a2+b2=4,c2+d2=16，证明|ac+bd|≤8.

新题3 已知a,b,c,d为实数，且a2+b2=4,c2+d2=16，证明|ac-bd|≤8.

新题4 已知a,b,c,d为实数，且a2+b2=m2,c2+d2=n2,m>0,n>0,，证明|ac+bd|≤mn.

新题5 已知a,b,c,d为实数，且a2+b2=m2,c2+d2=n2,m>0,n>0,，证明|ac-bd|≤mn.

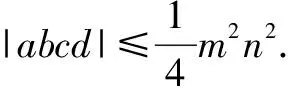
新题7 已知a1,a2,…,an;b1,b2,…,bn为实数,

新题8 已知a,b,c,d为实数，且a2+b2=4,c2+d2=16,ab+bd=8,证明ac-bd=0.

三、拓展体验

在一题多解和多变的拓展中，学生们可以看到不同知识块间的相关性(有利于形成知识链)，还可以看到不同人思维的差异(从别人的思维中获得启迪)，还可以看到建立在独立思考基础上的合作交流意义重大. 在一题多解，一题多变的拓展中，学生们看到了一题多法，多题一法，看到了特殊与一般的转化. 在拓展的过程中，学生们的情感体验也在变化：或感叹于我怎么没想到，或惊叹数学的神奇，或陶醉于心理的积极暗示——下一次，我也要多想想，多试试. 不难看出，这样的拓展是对已有资源更充分的利用，对学生探究意识和能力的形成具有很大的促进作用.