巧用换元法构造导数定义解一类压轴题

纪定春 蒋红珠

(1.四川师范大学数学科学学院 610068;2.广东省华南师范大学数学科学学院 510631)

一、导数与不定式极限简介

高考数学注重对基础知识、基本概念及数学思想方法的考查.导数的定义是高中数学中重要的概念，是高考数学考查的重点，以导数的定义命题历来受到高考数学命题者的青睐.目前，大部分高中数学教师并不重视对数学概念的教学，正如章建跃先生所讲：“当下的概念课教学多是一种走“形式化”的过程，以解题教学代替概念教学的现象比较普遍.”这种以解题教学培养出来的学生，在考场上碰到用概念或定义来解决的试题将感到很困难.因此，高中数学教学要注重数学概念的教学.导数的定义是解决高考数学函数压轴题中“不定式”极限的好方法，接下来将对导数的定义和不定式极限作简单的介绍.

导数的定义简介设函数y=f(x)在x=x0处的瞬时变化率为

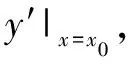
这就是函数定义在点x=x0处的导数.

不定式极限简介若函数f(x)和g(x)满足：

二、巧用换元法构造导数定义解高考压轴题

1.在求参数值中的应用

例1(2017年全国高考数学卷Ⅲ第21题)已知函数f(x)=x-1-alnx.

(1)若f(x)≥0，求a的值；

(2)略.

解析对问题(1)，要使f(x)≥0，等价于x-1-alnx≥0.

考虑分离参数a，显然需要分类讨论.

当x=1时，有f(x)≥0，所以a∈R.

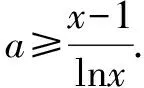
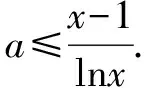
该极限显然为一个“不定式”极限，考虑使用换元法，将该分式极限构造成导数的定义来求解.

令lnx=y，显然有x=ey.

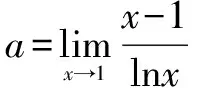
考虑构造函数g(y)=ey，则g(0)=1.

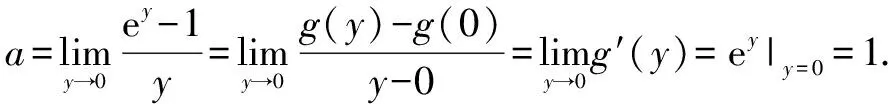
综上，a的值为1.

评注该试题巧用换元的思想，将所求极限的分母lnx换成y，将所求极限的分母构造出导数定义的结构形式，然后根据换元后的分母结构，选择函数g(y)=ey作为求导函数，这样就将求“不定式”极限问题转化为求函数g(y)在y=0处的导数问题.

2.在求参数取值范围中的应用

例2(2010全国高考数学新课标理科卷第21题)设函数f(x)=ex-1-x-ax2.

(1)若a=0，求f(x)的单调区间；

(2)若当x≥0时f(x)≥0，求a的取值范围.

解析问题(1)略.

对于问题(2)，显然可以使用参数分离法，故需要对x进行分类讨论.

当x=0时，不等式显然成立，故a∈R.

令h(x)=xex-2ex+x+2，可得h′(x)=xex-ex+1.

再对h′(x)求导数，可得h″(x)=xex.显然，当x>0时，h″(x)≥0.

所以h′(x)≥h′(0)=0，h(x)≥h(0)=0.

故有g′(x)≥0，则函数g(x)在x>0时单调递增.

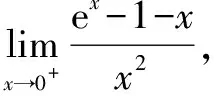
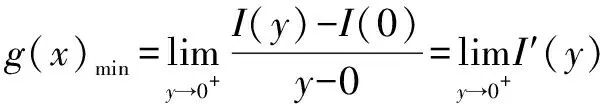
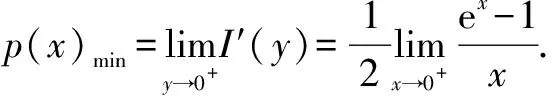
又令J(x)=ex，则有J(0)=1.

评注该试题两次巧用换元法，将不定式极限转化成可以求解的导数结构.通过第一次求导，将该极限的分母由平方变成了一次方，这和结构显然符合导数的定义.然后选取“J(x)=ex”作为函数，直接构造导函数的定义，将无法直接求极限的分式式“I′(y)”转化为可求极限的整式结构“ex”.这两次构造都充分的利用导数定义和换元的思想.

3.在求不等式恒成立中的应用

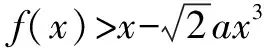
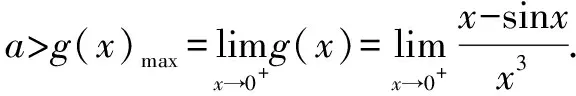
该极限为“不定式”极限，分母为三次单项式，不能直接利用导数的定义，故考虑换元法，将分母换成导数定义的结构.

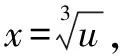
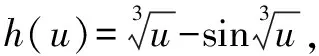
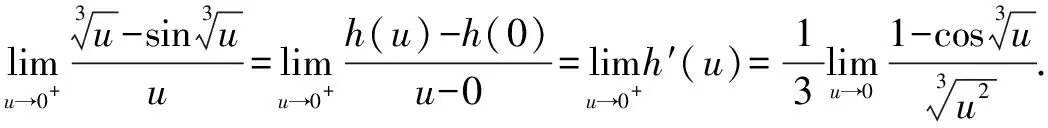
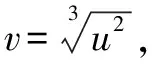
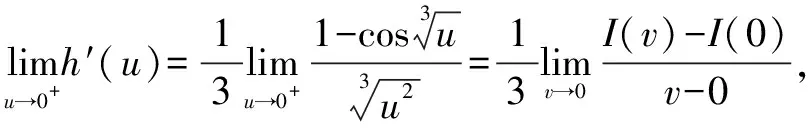
设J(w)=sinw，则有J(0)=0.

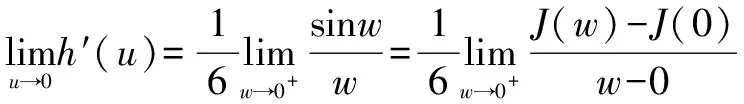
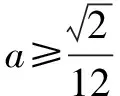
评注该试题多次使用换元法，将极限的分母换成一次单项式，这样做是为了构造出导数定义的分母结构，然后逐次利用导数的定义，将分母的三次式逐渐降阶，把不定式极限问题转化成一个整式的极限问题.可见，在该题中用换元法构造导数的定义具有“降次”的作用，最终将所求极限的分母变成0次项.

通过对上述试题的解析，可见导数的定义是解决高考函数压轴题的强大工具.当遇到不定式求极限问题，可以考虑使用换元法，将所求极限的分母换成导数定义的结构，然后根据分母的结构来构造函数，分子函数的选择要与分母的结构相匹配，要让构造出来的结构和导数的定义相吻合.对于上述例题，很多考生很难想到使用换元的方法，将求“不定式”的问题转化成用导数的定义来解决.这表明，绝大部分高考考生对用导数的定义来解决“不定式”极限问题并不熟悉，因此，高中数学教学要强化对数学核心概念的学习，而不是走过场式的“形式化”学习.