多层土压密注浆抬升时上抬力计算分析

李小丰

多层土压密注浆抬升时上抬力计算分析

李小丰

(中铁十八局集团 第五工程有限公司，天津 100855)

建筑物注浆的关键是经过注浆后对既有建筑物的抬升效果进行动态控制和工后恢复，以此减小建筑物的不均匀沉降。考虑三维破坏机制，采用非线性Mohr-Coulomb破坏准则构建一个轴对称的土体破坏机制，对压密注浆的抬升作用进行力学分析。基于极限分析上限定理，通过变分计算求出单个土层地表隆起时上抬力的表达式，再将表达式推广到各个土层，得到多层土注浆抬升时上抬力的求解方程和土体破坏面的上限解，结合前人的计算结果对比分析来验证本文理论的正确性。

多层土；三维破坏；上抬力；注浆；非线性破坏

注浆抬升技术的原理是利用注浆过程中浆液产生的上抬力使建筑物发生上抬位移，其最早是用于建筑物的纠偏。初期注浆技术大部分应用于地基加固或防渗处理工程中，而在压密注浆中产生的上抬力和地表隆起现象则一直被认为是此工艺产生的不利影响。直到20世纪80年代，其抬升作用的正面影响才逐渐被人们所重视，工程人员也逐渐开始尝试在实际工程中利用这种正面影响。Graf[1]提出可以利用压密注浆的抬升效应来纠正建筑物的偏差，认为压密注浆的主要用途是通过挤密土体改善土体性能，还可以通过土体中形成的桩体抬起建筑物，用于发生不均匀沉降的建筑物纠偏。Bolton等[2]对软黏土地层中进行隧道掘进时压密注浆的抬升效应进行研究，分析了其对地层变形的影响规律，并指出在超固结黏土中的注浆效果比在正常固结黏土中好。易小明等[3]通过相关分析和数值模拟，对注浆抬升参数选取进行了初步优化，对房屋的抬升量进行了预测。董葳[4]研究了劈裂注浆、压密注浆和渗透注浆3种注浆方式之间的区别，并采用数值模拟的方式开展了深入研究。章敏等[5]推导出了多浆泡在均匀及非均匀2种扩张模式下地表抬升变形的理论计算公式及其简化形式。李梦天等[6]根据随机介质理论建立注浆抬升计算方法及简化算法，分别研究压密注浆与劈裂注浆对地表抬升的影响机制。唐智伟等[7]构建了关于土体体积应变增量、土体位移量及注浆量关系的模型，通过对注浆单元体施加膨胀压力模拟了单孔注浆时注浆抬升量，并分析了注浆抬升的变化规律。现有研究大多都是定性分析、试验拟合或数值模拟研究，注浆过程中土层真实的破坏情况和土体层数往往没有考虑，压密注浆压力及注浆引起地表隆起时上抬力的计算也很少涉及且没有考虑三维破坏的情况。考虑三维破坏机制，基于非线性Mohr-Coulomb破坏准则和极限分析上限定理，本文通过变分计算得到多层土注浆抬升时上抬力的求解方程和土体破坏面的上限解。结果表明，在相同计算条件下2种计算方法得到的注浆上抬力有一定的差值，导致的原因可能是考虑多层土时，其注浆深度往往要比单层土时的注浆深度大，所以在相同的浆泡半径下注浆上抬力也更大。本文提出的计算方法可用于工程中压密注浆抬升时注浆压力选取。

1 问题陈述

现有研究中对于压密注浆压力及上抬力的确定是综合考虑浆泡扩张和土体锥形剪切破坏2种变形模式，然而针对土体锥形剪切破坏的研究仅仅只考虑二维平面内，很少涉及到三维土体模型的 计算。

采用ZOU等[8]提出的二维破坏曲线，通过绕轴旋转的方式将其改进为三维破坏模型，并忽略浆泡重力作用的影响，如图1所示。

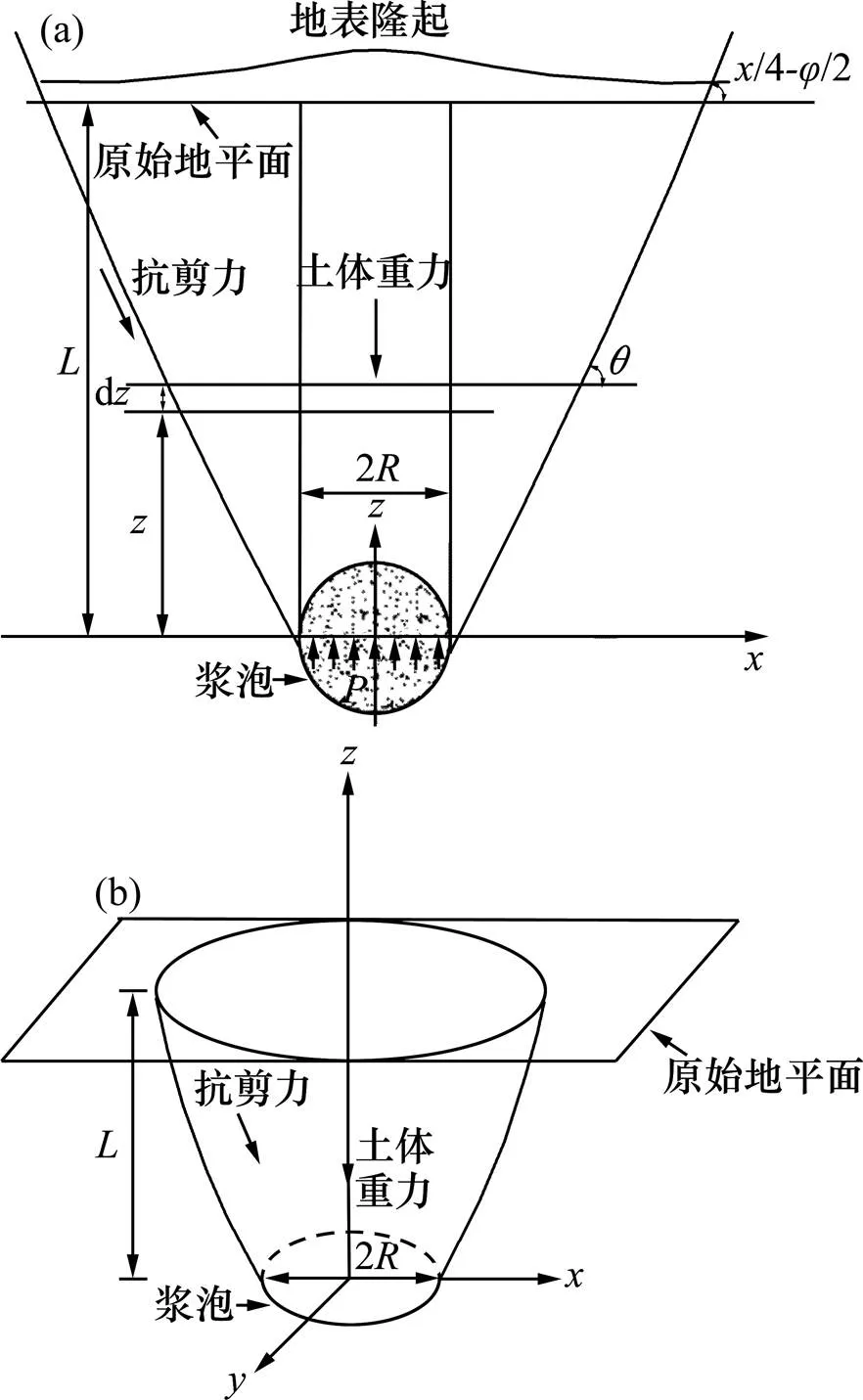
图1 浆泡的锥形剪切破坏模型

与二维破坏机制相比，三维破坏机制的构建是一个相对复杂的问题。然而，考虑到球对称的关系，在一个同心球面上的所有点都具有相同的应力状态，轴对称破坏机制更适合描述压密注浆过程中的土体变形模式。在前人研究的基础上，建立浆泡的轴对称破坏机制，如图1所示。

如图2所示，土体发生破坏的部分涉及了个土层，分别用土层1，土层2，…，土层表示，每个土层的垂直高度分别用1，2，…，H表示。轴对称破坏机制的具体构造过程如下：首先，由于每个土层的力学性能具有显著差异，在坐标系的半平面上建立由条曲线组成的二维破坏模型，这条曲线分别代表每个土层的破坏曲线，用1()，2()，…，f()表示。对于破坏曲线的连续性，假定相邻曲线在土体界面上相交于一点，交点的横坐标分别是1，2，…，L。其次，将二维破坏曲线绕轴旋转360度，建立三维轴对称破坏机制，由破坏曲线旋转形成的破坏面为速度不连续面。

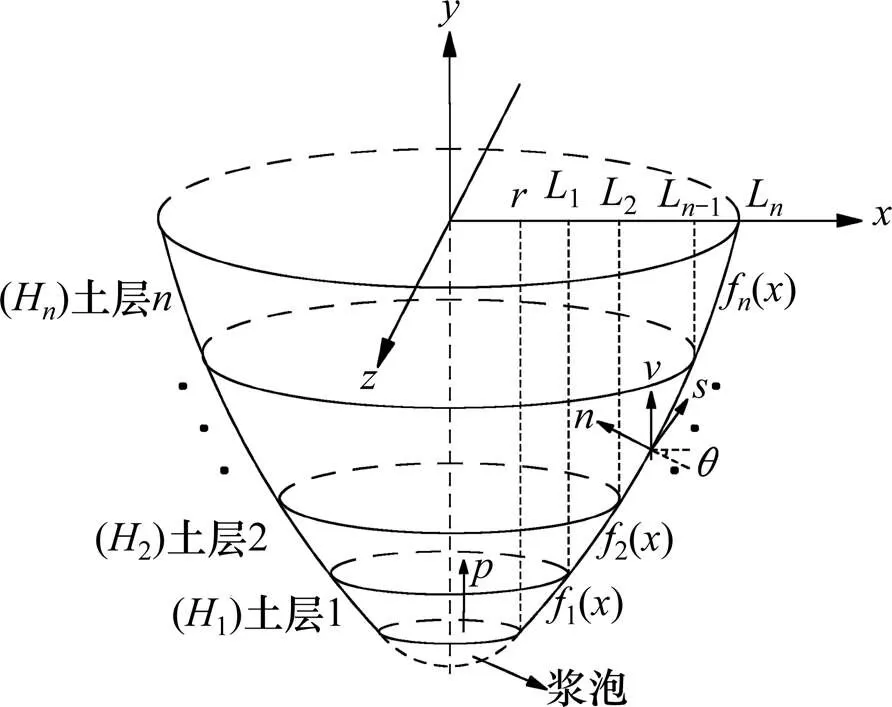
图2 多层土中土体破坏机制

2 理论和方法

2.1 非线性Mohr-Coulomb破坏准则

自首次提出以来，线性Mohr-Coulomb破坏准则被广泛应用于描述土体的特征强度。然而，许多实验表明在σ−τ应力空间中，土体的破坏包络线并不是线性的，线性Mohr-Coulomb破坏准则仅仅是一个特例。因此，非线性Mohr-Coulomb破坏准则更适合于土体结构的变形分析。基于此，本文选择非线性Mohr-Coulomb破坏准则展开研究，其表达式如下[9−11]：

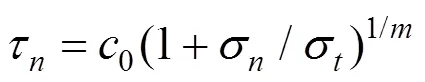
将式(1)绘制成如图3所示的曲线，式中：σ为法向应力；τ为切向应力；0，σ和均为土体的材料参数，具体值的选取可以通过室内试验决定；0和σ分别是曲线与纵轴和横轴的截距，曲线恒定通过(0,0)和(−σ,0)2个点；是决定曲线弯曲程度的非线性系数，当=l时，式(1)变为线性Mohr- Coulomb破坏准则。

2.2 上限定理

上限定理是解决土体结构稳定问题的有效方法，其定义如下：对于满足速度边界条件、几何方程和体积不变条件的任意速度场，由虚功方程确定的荷载肯定大于或等于其真实荷载，其表达式为：

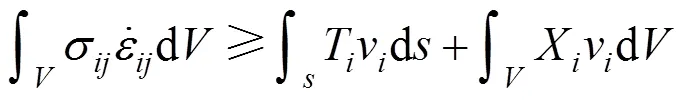
式中：σij和分别为运动许可速度场中的应力张量和应变率张量；Ti为附加在边界上的荷载；Xi为体力；V为土体破坏部分的体积；vi是沿速度不连续面的速度。

因为上限定理的前提条件是土体被假定为理想塑性介质并忽略其几何变形，所以基于2点假设建立轴对称三维破坏机制：1) 浆泡上方土体均服从相关联流动法则；2) 浆泡上方土体均为理想刚塑性体，发生破坏时符合非线性M-C准则。

3 上抬力求解

3.1 单层土破坏机制

为了研究方便，本节首先研究单一土层中浆泡的轴对称破坏机制。基于相关联流动法则和非线性Mohr-Coulomb破坏准则，可以先对速度不连续面上的法向和切向应力−应变进行求解，再推导出速度不连续面上任意点的内部能量耗散功率。

对于遵从相关联流动法则的材料(称之为标准材料)，其塑性势面必须与屈服面相同，并且塑性应变增量也必须与塑性势的应力梯度成正比例关系。因此塑性势函数可以写为：

然后，将塑性应变率写成下面的形式：

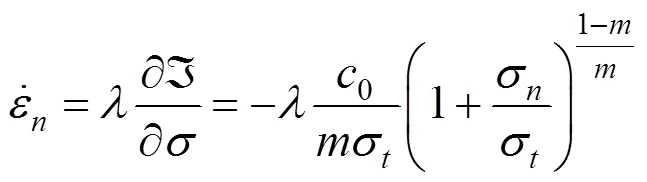
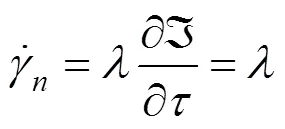
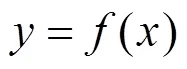
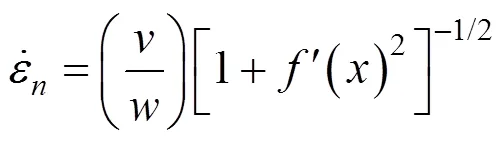
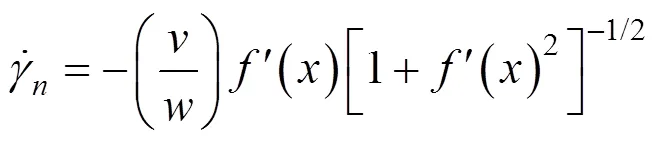
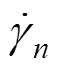
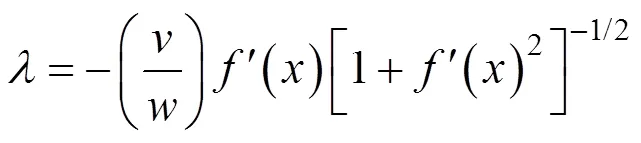
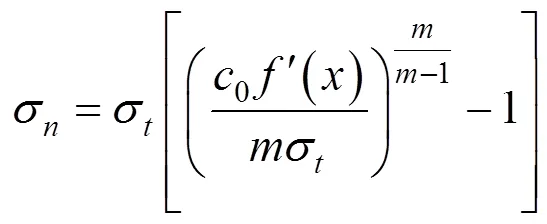
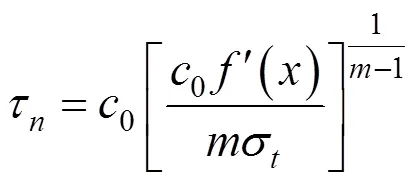
由此可以求得速度不连续面上任意点的内部能量耗散功率为：

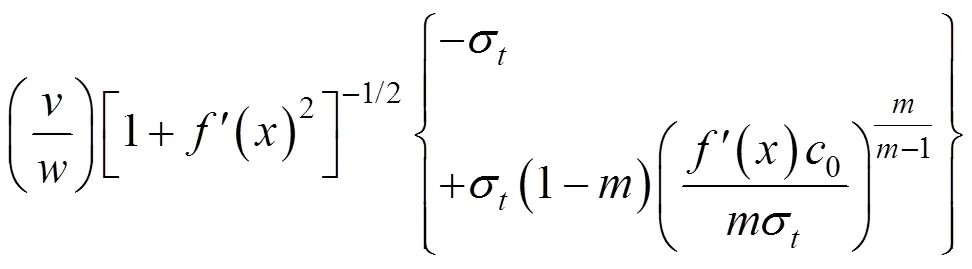
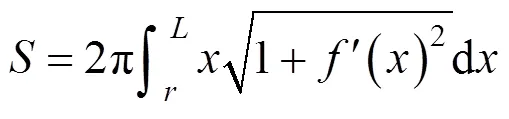
式中：是浆泡半径；1是相邻的速度不连续曲线第1个交点的横坐标。速度不连续破坏面上总的内部能量耗散可以通过对任意一点处的内能耗散功率积分求得，其表达式为：

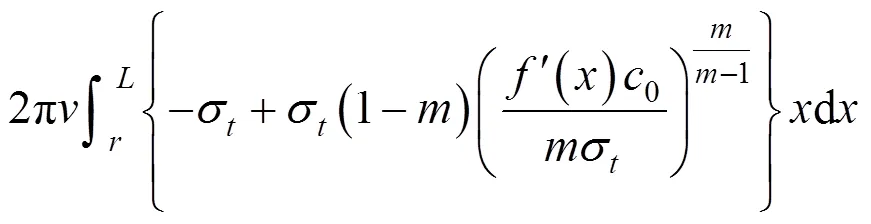
在坐标系中，旋转体的体积可以写成如下表达式：

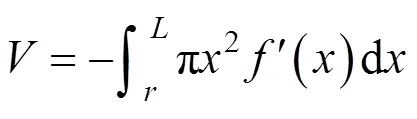
将土体的容重乘以旋转体的体积，可以得出土体破坏部分总的重力功率，其表达式为：

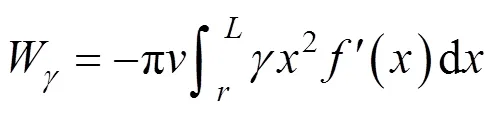
式中：是土体重度。

发生抬升作用时注浆压力1的总功率为：

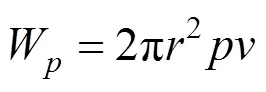
根据上限定理，总外力功率等于总内能耗散功率，于是有：

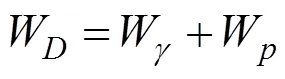
将式(11)，(13)和式(14)代入式(15)，可求得发生抬升作用时浆泡所施加的上抬力的表达式为：

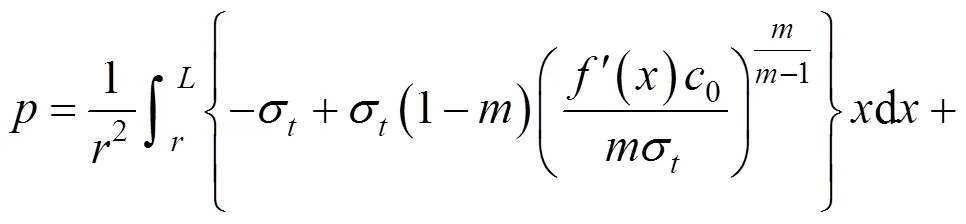
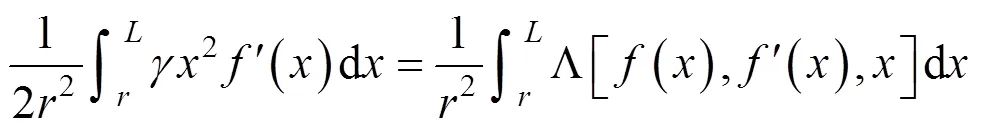
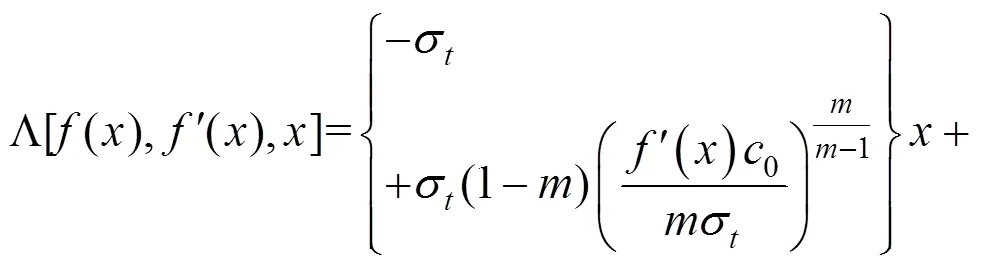
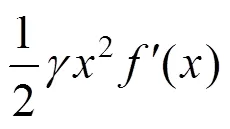
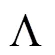
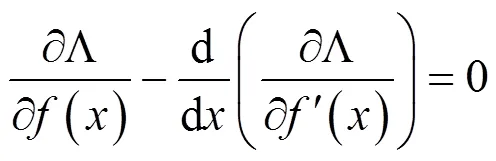
将式(17)代入式(18)中，可以得到以下的微分方程为：

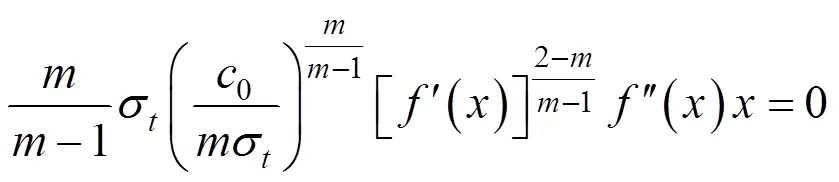
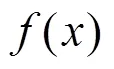
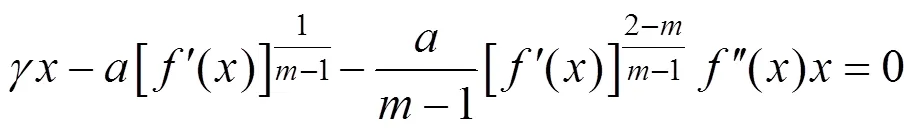
其中：

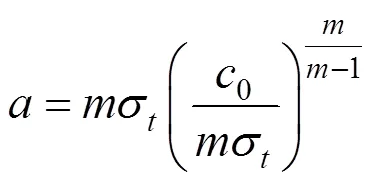
不难发现，式(20)是不显含()的二阶方程，可以利用替代法降阶为一阶方程，通过分层法将土体看成若干个土层，每一层土体的破坏曲线()近似为直线，于是有：

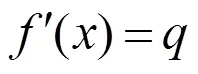
则()的二阶导数可以表示为：

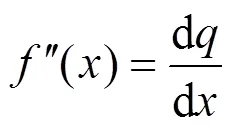
将式(22)和式(23)代入到式(20)中，可以得到以下等式：

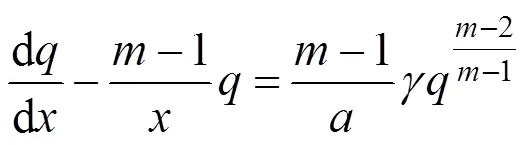
由式(24)可以看出，它是一个伯努利方程，可以通过变量代换转换成一个线性微分方程。为了实现这一变量代换，可以令：

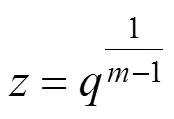
将式(25)代入到式(24)中，原等式可以化简为：

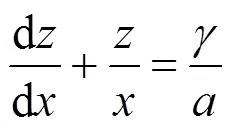
很明显可以看出，式(26)为一阶非齐次微分方程，可以通过常数变易法求出其通解的表达式为：

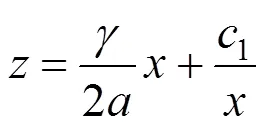
式中：1是一个积分常数，可由边界条件确定。

将式(25)代入式(22)中，可以得到以下表达式：

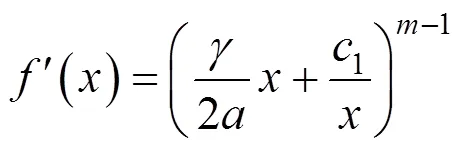
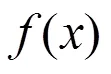
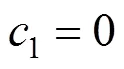
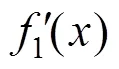
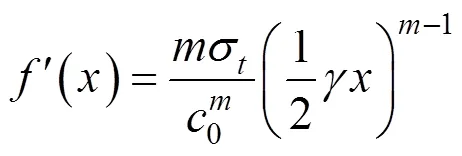
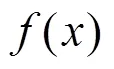
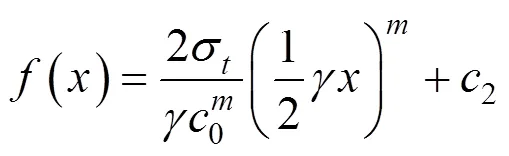
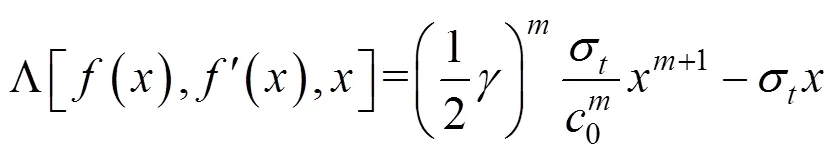
将式(33)代入式(16)并积分，可以得到发生抬升作用时浆泡所施加的上抬力的表达式为：

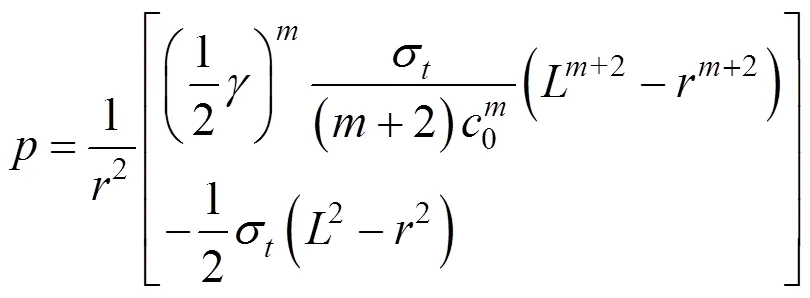
3.2 多层土破坏机制

对于多层土，不同土层的力学性质有明显的差异，为了容易区分，用下标1，2，…，表示土层1到土层的力学参数。与前面的分析类似，每一层都应该满足上限定理，即总外力功率等于总内能耗散功率。虽然其力学性质不同，但各土层的内能耗散功率与式(9)相同，由此可以首先计算每一土层速度不连续破坏面上总的内部能量耗散，其表达式分别为：

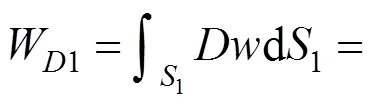
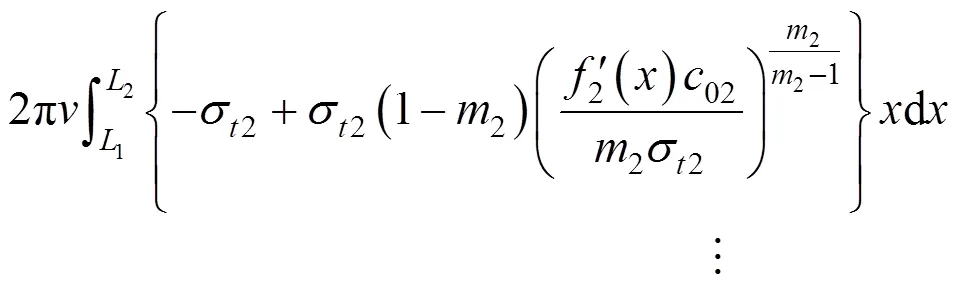
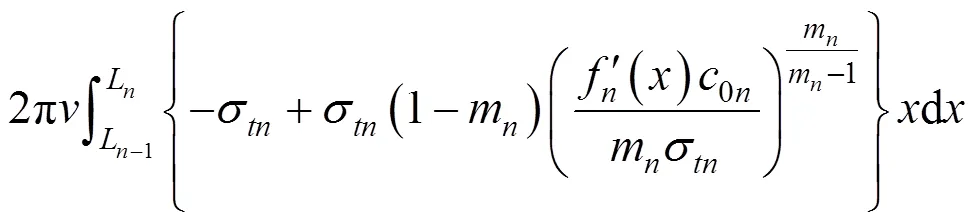
式中：是浆泡半径；1，2，…，L是相邻速度不连续破坏曲线交点的横坐标。

类似于式(13)，可以再计算每一层土体破坏部分总的重力功率，其表达式分别为：

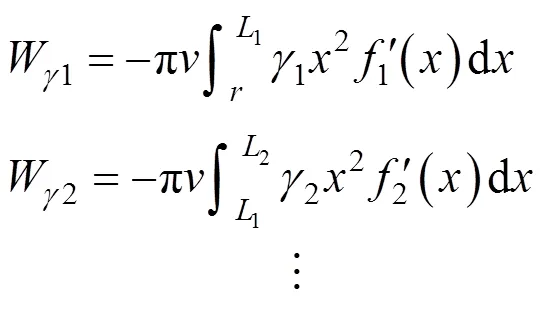
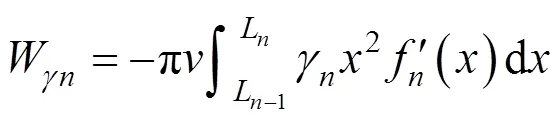
不同的是，发生抬升作用时浆泡所施加的上抬力的总功率求法不一样。对于土层1，其上抬力的作用面是浆泡的上表面；对于土层2到土层，其作用面可以看成是近似圆面。所以每一土层上抬力的总功率的表达式分别为：

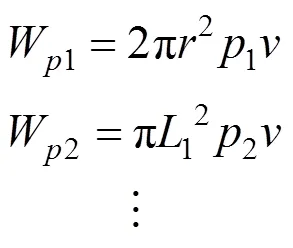
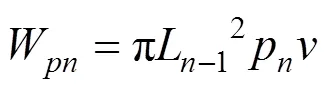
由于每一层土都应该满足总外力功率等于总内部能量耗散功率，于是应该有：

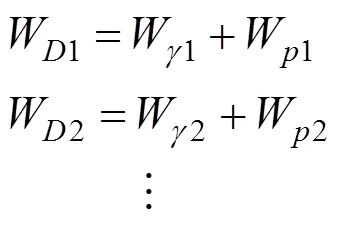
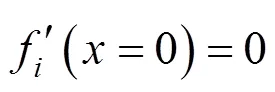
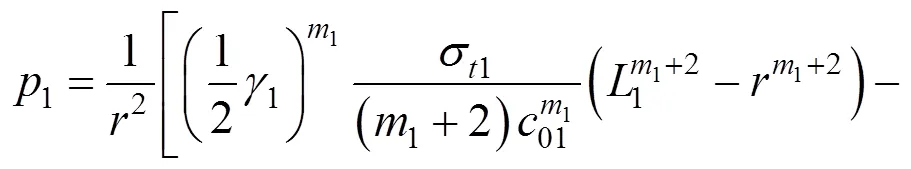
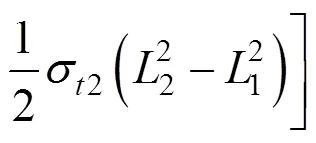
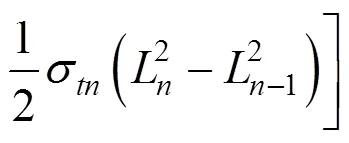
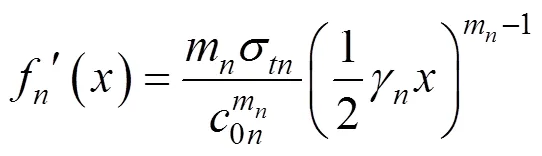
那么发生抬升作用时浆泡所施加的整个上抬力即为各个土层的上抬力p(=1，2，…，)之和，于是其表达式为：

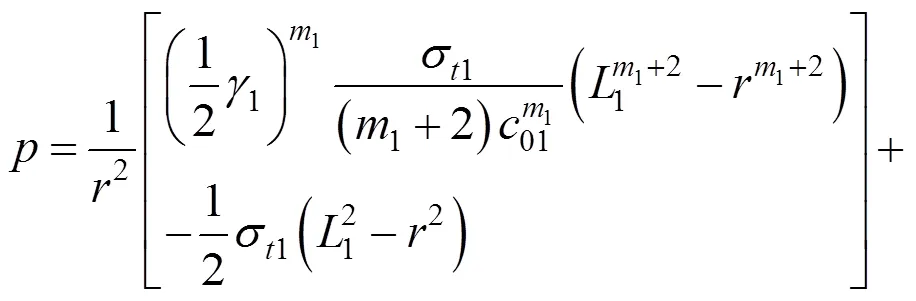
由于土层力学性质不同，交叉点相邻速度不连续破坏曲线斜率不相等。因此，相邻破坏曲线的连接不再光滑，这与多层土中注浆时的土体破坏特征是一致的。通过对式(41)进行积分，可以得到速度不连续破坏曲线的表达式为：

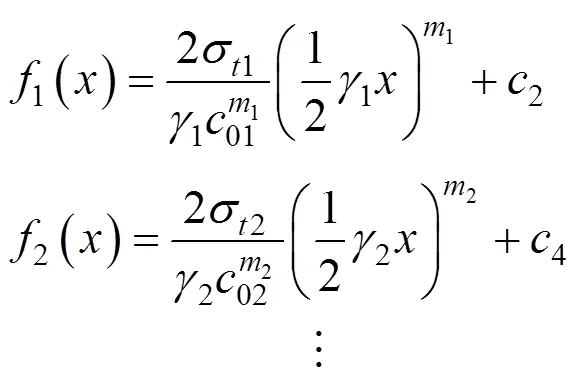
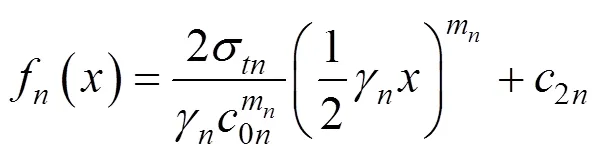
式中：2，4，…，2n是积分常数。

考虑到速度不连续曲线的连续性，应满足下列边界条件：

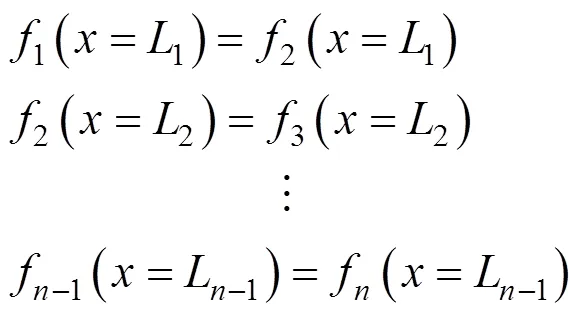
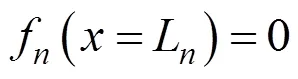
将式(42)代入到式(43)中，可以得到积分常数的表达式为：

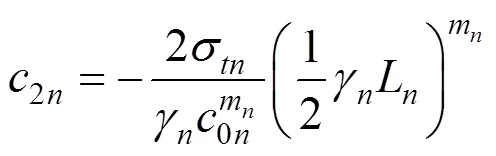
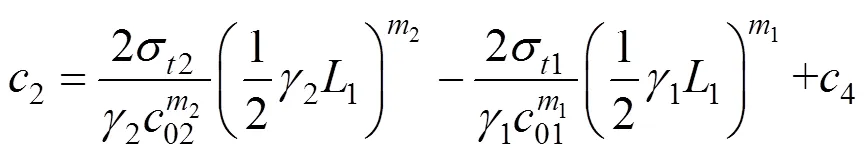
从式(44)可以看出，当已知1，2，…，L的值时，积分常数2，4，…，2n的值可以通过迭代的方法求得。因此，式(41)和式(44)中均只有个未知数1，2，…，L，考虑到交叉点的坐标与土层高度有关，可以得到−1个边界条件：

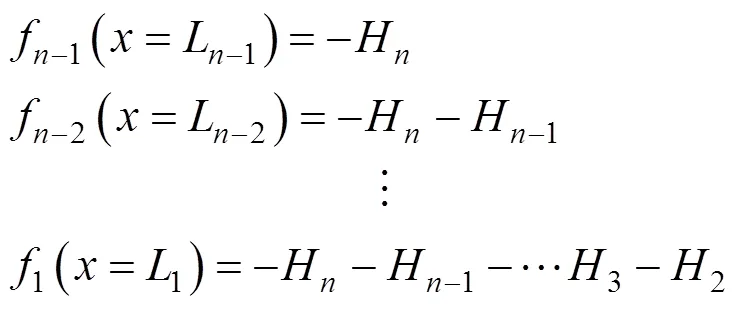
3.3 计算方法

虽然在之前的分析中已经表明了含个土层的轴对称破坏机制，但仍然存在计算问题。为了解决这个问题，计算程序假定破坏机制首先只涉及一个土层；然后，将=1代入得到的解析表达式中，建立非线性方程；其次通过求解非线性方程，可以得到第1层破坏机制的未知参数和垂直高度，用表示。如果第1层破坏机制的垂直高度小于第1层土的高度，即：≤1，如图4(a)所示，得出的破坏机制是正确的，由此求出相应的上抬力，计算过程结束。如果>1，如图4(b)所示，轴对称破坏机制涉及到上部土层。在这种情况下，计算程序重新开始，土层数增加1，即=2。当第1层破坏机制的计算高度小于第1层的高度时，该计算过程最终停止。具体的计算流程如图5所示。

4 验证与分析

为了验证本研究的正确性，重点讨论涉及2个土层的注浆上抬力和破坏面，将本章单层土与多层土的求解结果进行对比分析。采用的计算参数为：01=30 kPa，02=45 kPa，σ1=40 kPa，σ2=55 kPa，1=17 kN/m3，2=21 kN/m3，1=1.6，2=1.4和1=4 m，通过MATLAB编程计算得到了多层土中压密注浆上抬力与浆泡半径的变化规律，如图6所示，同时还得到了压密注浆抬升时土体发生剪切破坏的破坏面形式，如图7所示。

如图6所示，多层土中压密注浆时浆泡对土体产生的上抬力与浆泡半径成反比例关系。对比结果表明，相同计算条件下2种计算方法得到的注浆上抬力有一定的差值，导致的原因可能是考虑多层土时，其注浆深度往往要比单层土时的注浆深度大，所以在相同的浆泡半径下注浆上抬力也更大。图7中显示的土体破坏面形式也服从实际土体中的破坏情况，因此可以验证本文所提出的注浆上抬力和破坏面的求解计算方法是具有可靠性与准确性的。

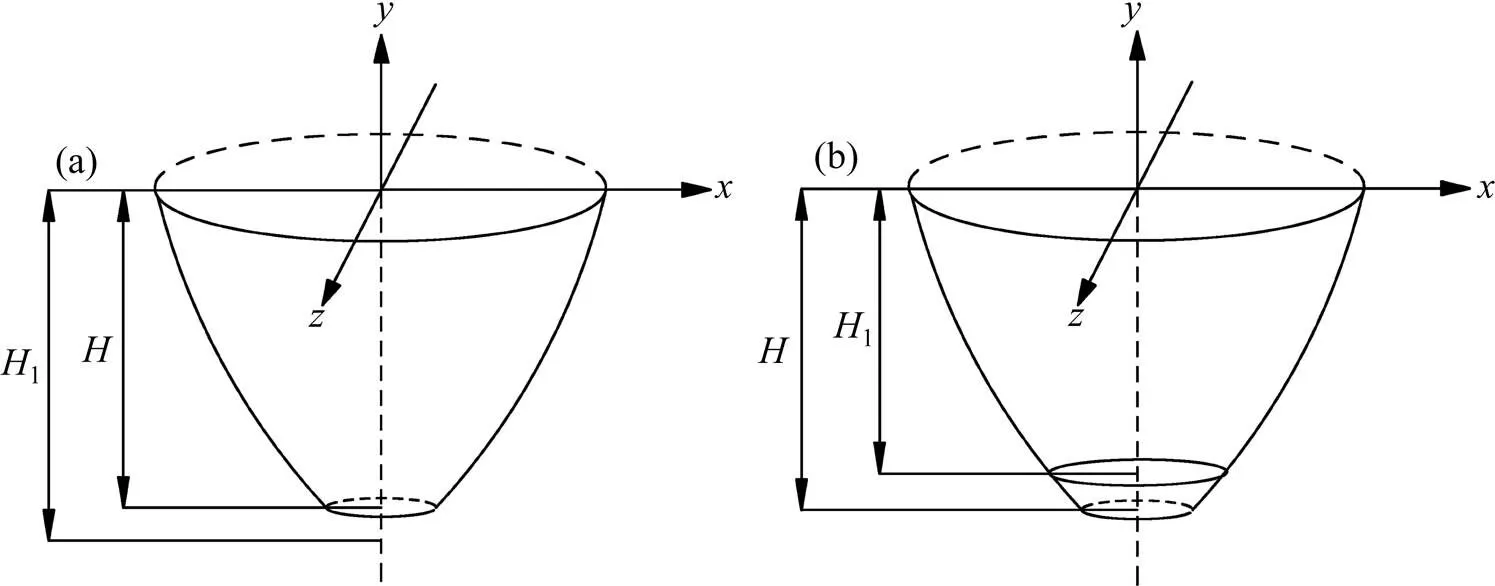
(a) H≤H1；(b) H>H1

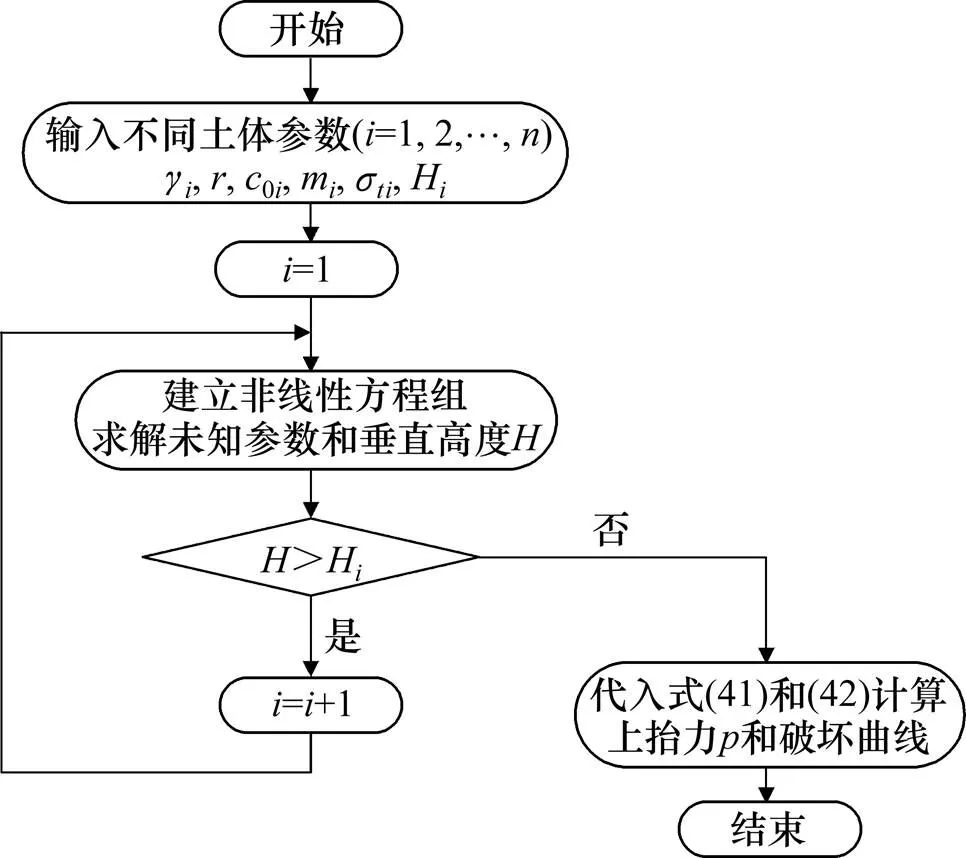
图5 计算流程图

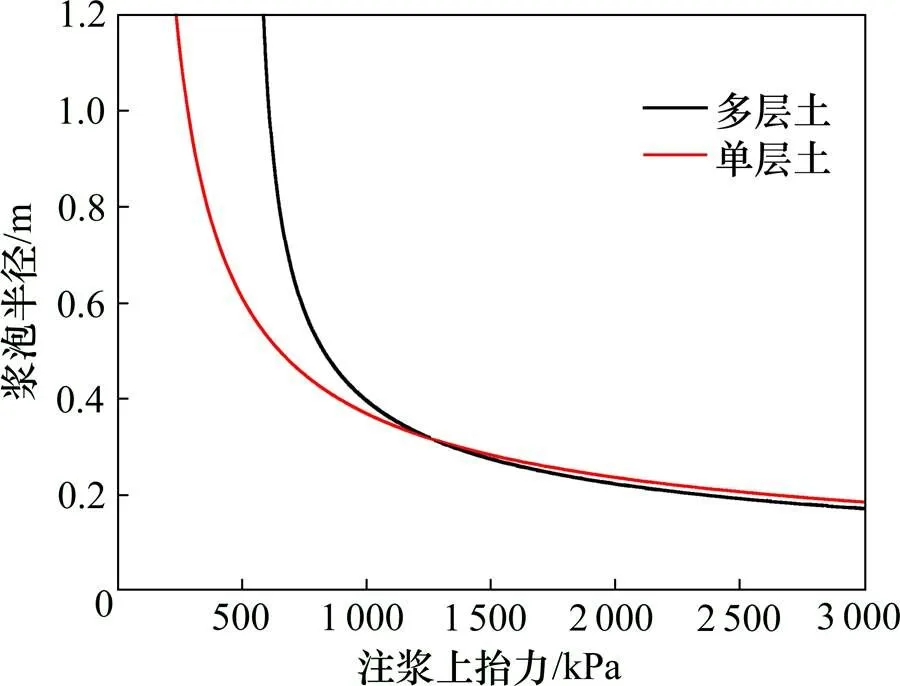
图6 注浆上抬力与浆泡半径的变化曲线

图7 破坏面形式

5 结论

1) 考虑三维破坏机制并基于非线性Mohr -Coulomb破坏准则和极限分析上限定理，通过变分计算得到多层土注浆抬升时上抬力的求解方程和土体破坏面的上限解。

2) 通过对比研究结果表明，考虑多层土时在相同的浆泡半径下注浆上抬力也更大。

3) 本文提出的计算方法可用于工程中面对复杂工况时考虑多层土情况的压密注浆抬升时注浆压力的选取。

[1] Graf E D. Compaction grouting technique and observations[J]. Journal of Soil Mechanics and Foundations Div, 1969, 95(9): 1151−1158.

[2] Bolton M D, Soga K, Jafari M R, et al. Soil consolidation associated with grouting during shield tunnelling in soft clayey ground[J]. Géotechnique, 2001, 51(10): 835−846.

[3] 易小明, 张顶立, 逄铁铮, 等. 房屋注浆抬升实践与监测分析[J]. 岩土力学, 2009, 30(12): 3776−3782. YI Xiaoming, ZHANG Dingli, PANG Tiezheng, et al. Practice and monitoring analysis of grouting uplifting in houses[J]. Rock and Soil Mechanics, 2009, 30(12): 3776−3782.

[4] 董葳. 注浆抬升的数值模拟及抬升规律研究[D]. 北京:北京交通大学, 2014. DONG Wei. Grouting lifting numerical methods based on numerical simulation and model experiment[D]. Beijing: Beijing Jiaotong University, 2014.

[5] 章敏, 刘军军, 秦文权. 注浆抬升位移预测及简化模型研究[J]. 太原理工大学学报, 2015, 46(3): 298−302.ZHANG Min, LIU Junjun, QING Wenquan. Study on prediction and simplified model of grouting lifting displacement[J]. Journal of Taiyuan University of Technology, 2015, 46(3): 298−302.

[6] 李梦天, 张霄, 李术才, 等. 基于数值模拟和模型实验的注浆抬升计算方法[J]. 哈尔滨工业大学学报, 2019, 51(8): 159−166. LI Mengtian, ZHANG Xiao, LI Shucai, et al. Calculation method of grouting lift based on numerical simulation and model experiment[J]. Journal of Harbin University of Technology, 2019, 51(8):159−166.

[7] 唐智伟, 赵成刚. 注浆抬升地层的机制、解析解及数值模拟分析[J]. 岩土力学, 2016, 29(6): 1512−1516. TANG Zhiwei, ZHAO Chenggang. Mechanism, analytical solution and numerical simulation analysis of grouting uplifting stratum[J]. Rock and Soil Mechanics, 2016, 29(6): 1512−1516.

[8] ZOU J F, XIA M Y. Uplift Capacity of shallow anchors based on the generalized nonlinear failure criterion[J]. Mathematical Problems in Engineering, 2016, ID: 308047.

[9] ZHANG X J, CHEN W F. Stability analysis of slopes with general nonlinear failure criterion[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1987, 11(1): 33−50.

[10] SUN Z B, LIANG Q. Back analysis of general slope under earthquake forces using upper bound theorem[J]. Journal of Central South University, 2013, 20(11): 3274− 3281.

[11] SUN Z B, QIN C B. Stability analysis for natural slope by kinematical approach[J]. Journal of Central South University, 2014, 21(4): 1546−1553.

Calculation and analysis of uplifting force in multi-layer soil compaction grouting

LI Xiaofeng

( The 5th Company of the China Railway 18th Bureau Group Co., Ltd, Tianjin 100855, China)

A key link in grouting construction is to dynamically control the lifting effect of existing buildings and recover after grouting, in order to reduce the uneven settlement of buildings. Considering the three-dimensional failure mechanism, this paper constructed an axisymmetric soil failure mechanism using nonlinear Mohr-Coulomb failure criterion, and analyzed the uplifting effect of compaction grouting. Based on the upper bound theorem of limit analysis, the expression of the uplift force on the surface of a single soil layer was obtained by variational calculation, and then the expression was extended to each soil layer, finally the uplift force of multi-layer soil grouting was obtained. The upper bound solution of the equation and the failure surface of the soil was combined with the previous analysis results to verify the correctness of the theory.

multi-layered soil; three-dimensional failure; uplifting force; grouting; nonlinear failure

U455.49；TU472

A

1672 − 7029(2020)04 − 0931 − 09

10.19713/j.cnki.43−1423/u.T20190848

2019−09−20

国家科技重大专项项目(2017YFB1201200)

李小丰(1976−)，男，重庆人，高级工程师，从事铁路隧道工程设计、施工及相关研究工作；E−mail：756855722@qq.com

(编辑 阳丽霞)