模拟土与隧道相互作用的液压加载系统设计与试验应用
朱瑶宏,杨振华,陈飞飞,柳献
模拟土与隧道相互作用的液压加载系统设计与试验应用
朱瑶宏1,杨振华2,陈飞飞3,柳献2
(1. 宁波大学 建筑工程与环境学院,浙江 宁波 315211;2. 同济大学 地下建筑与工程系,上海 200092;3. 宁波华液机器制造有限公司,浙江 宁波 315131)
目前,盾构隧道整环足尺试验,其加载模式主要采用荷载控制。液压系统施加在结构上的荷载来源于静止土压力的计算值。这种加载方式采用荷载结构法的思想,难以反映作用在盾构隧道上的土压力随结构变形而改变的特性。针对以上不足,提出荷载位移曲线控制原理并将其应用于盾构隧道整环足尺试验。首先通过数值计算和地勘资料确定地层位移和地层抗力之间的关系,将其输入系统。然后观察此曲线与以液压缸顶力和行程为坐标的点的相对位置,通过调整液压缸顶力使得该点位于曲线上。此控制原理能够实现结构所受荷载随结构位移变化而变化,从而真实地模拟地层对盾构隧道的作用。在盾构隧道足尺试验中具有良好的应用前景。
结构试验;加载系统;荷载位移曲线控制

目前,结构试验中采用液压系统作为加载设备时加载方式有荷载控制和位移控制2种。荷载控制,即控制液压缸,使其施加在结构上的荷载为预设值,而不考虑其行程变化。位移控制,即控制液压缸,使其行程达到设定值,而不考虑其荷载变化。具体到盾构隧道整环足尺试验,王如路等[1]针对双圆盾构进行了静力加载试验,全程采用荷载控制。曹文宏等[2]针对上海长江隧道衬砌环进行了静力加载试验,全程采用荷载控制。何川等[3]采用荷载控制的加载思想,详细描述了如何由实际工程中的水土压力计算得到各液压缸试验荷载。Blom[4]等针对荷兰“绿色心脏”隧道进行了足尺试验研究,其全程采用了荷载控制技术。Jort等[5]对易北河隧道衬砌环进行了足尺试验,全程采用荷载控制,获得了其承载力和变形性能。毕湘利等[6]进行的盾构隧道整环足尺试验中,在弹性阶段采用荷载控制,当结构临近破坏时改用位移控制。综上所述,盾构隧道整环足尺试验中最常用的加载控制方式是荷载控制,当结构临近破坏,各液压缸行程急剧增大,而荷载却几乎不能增加时,则采用位移控制的加载方式。这种加载模式,能够充分展现出结构本身的受力性能,但难以反映出周围土体对盾构隧道的作用。盾构隧道所受到的荷载,受到结构变形的影响。以土层中的盾构隧道为例:当结构没有位移时,结构受到静止土压力的作用。若在水土荷载的作用下,结构发生背离土层的位移,则其所受到的土压力将会减小,直至达到主动土压力。若在水土荷载作用下,结构发生朝向土层的位移,则其所受到的土压力将会增大,直至达到被动土压力。为了模拟盾构隧道所受荷载随结构位移变化这一特点,有必要研究出一种新的加载方式。这种加载方式满足以下要求:液压缸活塞的行程和荷载关系符合特定的荷载位移曲线,且这条荷载位移曲线与周边土体的本构关系相契合。将这种加载方式命名为荷载位移曲线控制。
1 地层位移−地层抗力关系的获取
进行荷载位移曲线控制的基础是已知土体的地层位移−地层抗力关系。土力学已经给出了定性的地层荷载位移曲线,不妨假设该关系的函数表达式为(),如图1所示。

图1 土压力变化趋势
进行荷载位移曲线控制需要定量的地层荷载位移曲线。目前,定量的地层位移—地层抗力关系的获取方法,主要有试验,解析解法和数值计算3种方法。
1.1 试验法
通过室内试验和原位试验,可以获得场地的基床系数。原位试验常采用K30方法[7],即采用直径30 cm的圆形荷载板进行水平加载试验和垂直加载试验,以获得水平基床系数和竖向基床系数。室内试验往往采用三轴试验或固结试验的方法测量基床系数。获得场地的基床系数后,以基床系数为斜率,做出一条直线,即可作为地层抗力-地层位移关系曲线。
试验法中涉及到的室内试验和原位试验,常在结构试验进行之前已经完成,其结果已经写入地勘报告。进行结构试验时,只需查阅即可,过程简单。但是,这种方法获得的地层位移-地层抗力关系是线性的,不能模拟土体的非线性力学特性,会造成较大的误差。
1.2 解析解法
1.2.1 深埋隧道
当隧道埋深足够大时,求解地层抗力—地层位移关系曲线可以简化为求解带圆孔无限空间内壁受法向压力的问题,此问题已有解。如图1,设隧道半径为,洞周径向荷载为,隧道埋深趋向于无穷。则孔周切向位移为0,孔周径向位移如式(1)[8]所示:

所以,周围地层的基床系数可以表示为式(2):
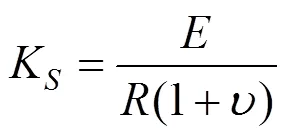
以基床系数为斜率,做一条直线,即地层位移−地层抗力关系。即此时其表达式如式(3)所示:
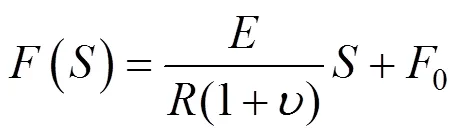
1.2.2 浅埋隧道
求解浅埋隧道的地层抗力—地层位移关系曲线,可以采用2种思路。第1种思路是从固体力学出发,求解一个开有圆孔的半无限平面孔周受到径向荷载的边值问题。
针对此问题,Verruijt[9]采用复变函数解法,求得带圆孔半无限空间内壁受法向压力作用时的位移场。如式(4),该位移场使用()和() 2个函数表达:
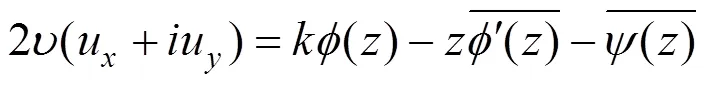
用孔周荷载除以求得的径向位移,即可得到基床系数。以基床系数为斜率,做一条直线,即地层位移−地层抗力关系。

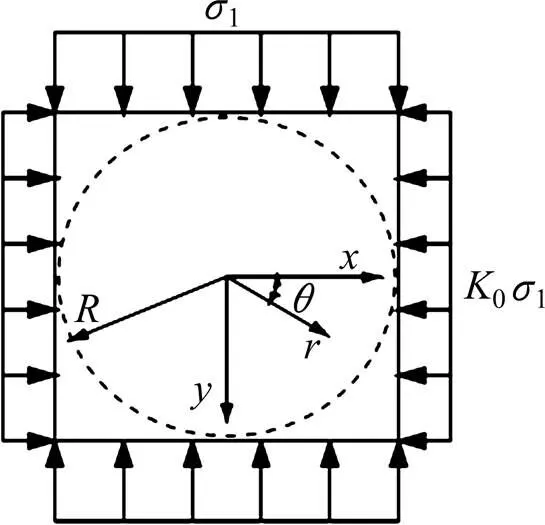
图2 土力学解析法计算示意
黄茂松等[10]通过求解此模型,得到切向土弹簧刚度K和径向土弹簧刚度K的表达式如式(5):

式中:为土层的剪切模量。对比黄茂松等[10]得到的径向土弹簧刚度和深埋隧道相应结果,可以发现二者具有一致性。
1.3 数值解法
由上一节中的分析可知,解析解法目前仅能对线弹性土体给出显式解,对更加复杂的土体本构无能为力。所以,在实际工程中,常用数值解法获得地层位移−地层抗力关系。
由弹性力学的圣维南原理推知,在静力计算中采用5倍于开挖宽度的计算域,边界的影响可以基本消除[11]。对于本问题,可以采用如下的几何模型进行计算:
计算区域宽度取为隧道直径的10倍,左右两端采用水平固定,竖向自由的边界,底部采用水平竖向均固定的支座,顶部采用自由边界。计算域范围上至地表,下至基岩上表面。
对计算域内土体划分网格后,采用适当的本构模型,逐级增加孔周荷载,算得径向位移。假设第级荷载大小为P,第级荷载作用下的地层径向位移为D,则地层的荷载位移曲线必定经过所有的(D,P)点,可以采用各种插值方法算得其表 达式。
如果采用拉格朗日插值,则地层的荷载位移曲线可以表示为式(6):

如果采用牛顿插值,则地层的荷载位移曲线可以表示为式(7):

2 荷载位移曲线控制模式的电气化实现
荷载位移曲线控制模式的电气化实现,既需要考虑到液压系统本身的工作原理,也需要考虑到试验结构和液压系统相互作用的原理。
2.1 液压系统工作原理
2.1.1 液压系统的控制目标
本文所述的液压系统需要实现以下控制目标。
假设土体固有的荷载位移曲线为(),式中:表示土压力;表示结构的位移。当0时,结构没有变形,结构所受到的土压力为静止土压力0,所以,土层固有的荷载位移曲线必过点(00),土体固有的荷载位移曲线如图1所示。
值得指出的是,()必然单调递增。因为当增大时,结构朝向土体的位移增大,土压力由静止土压力向被动土压力发展,土压力增大,增大。
进行试验时,首先采用荷载控制的加载方式,将液压缸荷载加载至静止土压力0,此时结构将产生变形0,即此时液压缸的荷载和活塞行程位于图1中空心圆点(00)。此时将加载系统调整为荷载位移曲线控制。加载系统自动识别到现在液压缸负载和活塞行程对应的点位于荷载位移曲线的下方,则液压系统自动地加大荷载,增大后,将会减小,液压缸荷载和活塞行程对应的点将沿着某一条路径来到土体固有的荷载位移曲线上(11)点,加载完成。
2.1.2 液压系统的控制装置
本文所采用的液压系统控制装置结构如图3 所示。

图3 控制系统示意
本文所采用加载系统,由PID控制器,比例放大器,伺服比例阀,液压缸,和压力/位移传感器构成。以下分别介绍其功能。
PID控制器是整个控制系统的核心元件。其工作原理如下:
首先,PID控制器接收压力/位移传感器传来的反馈电压信号u以及前置设备传来的目标值u,如式(8)所示,计算差值:

PID控制器输出的电压信号u按照式(9)计算:

其中:k为PID控制器的比例常数,其目的是控制系统消除u和u之间的差值;T是积分时间常数,用于消除静态误差;T是微分时间常数,其用途是提前预测信号变化的趋势,从而减少调节的时间。参数k,T和T的整定方法,采用文献[12]介绍的三维黄金分割自整定算法。
总而言之,PID控制器的功能是输出电压信号调节后续系统,使得反馈电压信号与目标电压信号趋于一致。
比例放大器的作用是将PID控制器传来的电压信号,放大并转化为电流信号,即如式(10)所示:
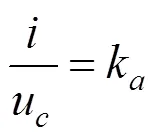
其中:k为比例放大器增益。
比例换向阀将比例放大器电流的变化转化为液压系统液压油流量的变化。其原理是电磁铁线圈中电流的变化将导致电磁铁与衔铁之间吸引力发生变化,导致电磁铁和衔铁间空隙发生变化,从而改变液压油的流量。本文所采用的比例换向阀遵循如式(11)的传递函数:

其中:K为比例换向阀增益。
液压缸是整个液压系统中的执行元件,它将液压系统中液压油的流量转化为作用在结构上的力。液压缸通过线性化流量方程,流量连续性方程,液压缸和负载力平衡方程3个基本方程建立起流量,负载力,阀芯位移,活塞位移等物理量之间的关系。即如式(12)~(14)所示:
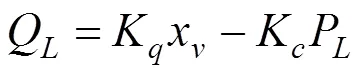

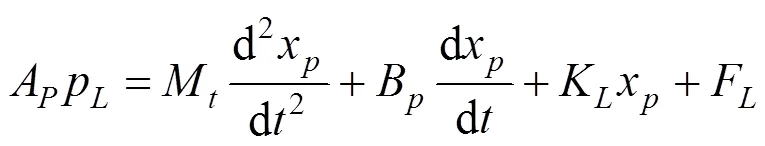
其中:Q表示液压缸流量;K为流量增益;K为流量−压力系数;x为阀芯位移;C为总泄露系数;P为负载压力;V为液压缸等效容积;β为体积弹性模量;A为平均活塞面积;x为活塞位移。
位移传感器将活塞位移转化为电压信号,即如式(15)所示:

其中:K为传感器传递系数。
2.1.3 液压系统的控制过程
设0时刻,活塞位移x(0),经位移传感器转化为电信号u(0)=Kx(0)。位移传感器将u(0)传递给计算机和PID控制器。计算机中内置有土层荷载位移曲线(),自动计算出此时荷载(0)(x(t)),计算机将(0)转化为电压信号u(0),并传输至PID控制器。PID控制器此时具有2个输入量,一是计算机传递的u(0),二是位移传感器传递的u(0),按照第2.2.1节的计算方法,依次给出(0)和u(0)。比例放大器按照第2.2.2节原理将u(0)转化为放大的电流信号(0)。伺服比例阀按照第2.2.3节原理将i(0)转化为系统流量变化(0)。液压缸按照第2.2.4节原理将(0)转化为负载压力AP(0),此时负载压力AP(0)应与(0)具有一致性。
当负载压力AP(0)作用在结构上时,由于荷载变化,结构的变形量发生变化,从而活塞行程随之由x(0)变为x(1)。重复上述调节过程,直至(t−1)(t)。此时液压缸活塞行程和负载(x(t)(t))位于预设的地层荷载位移曲线上,荷载位移曲线控制完成。值得指出的是,在试验过程中,液压缸加载梁与试验管片全程密贴,所以试验过程中x=s。
整个控制流程如图4所示。
2.2 结构−液压系统相互作用过程
结构−液压缸相互作用的过程,既包括结构与各液压缸的直接相互作用(1阶效应),也包括某个液压缸通过改变结构变形量从而间接影响其他液压缸荷载的间接相互作用(2阶效应)。
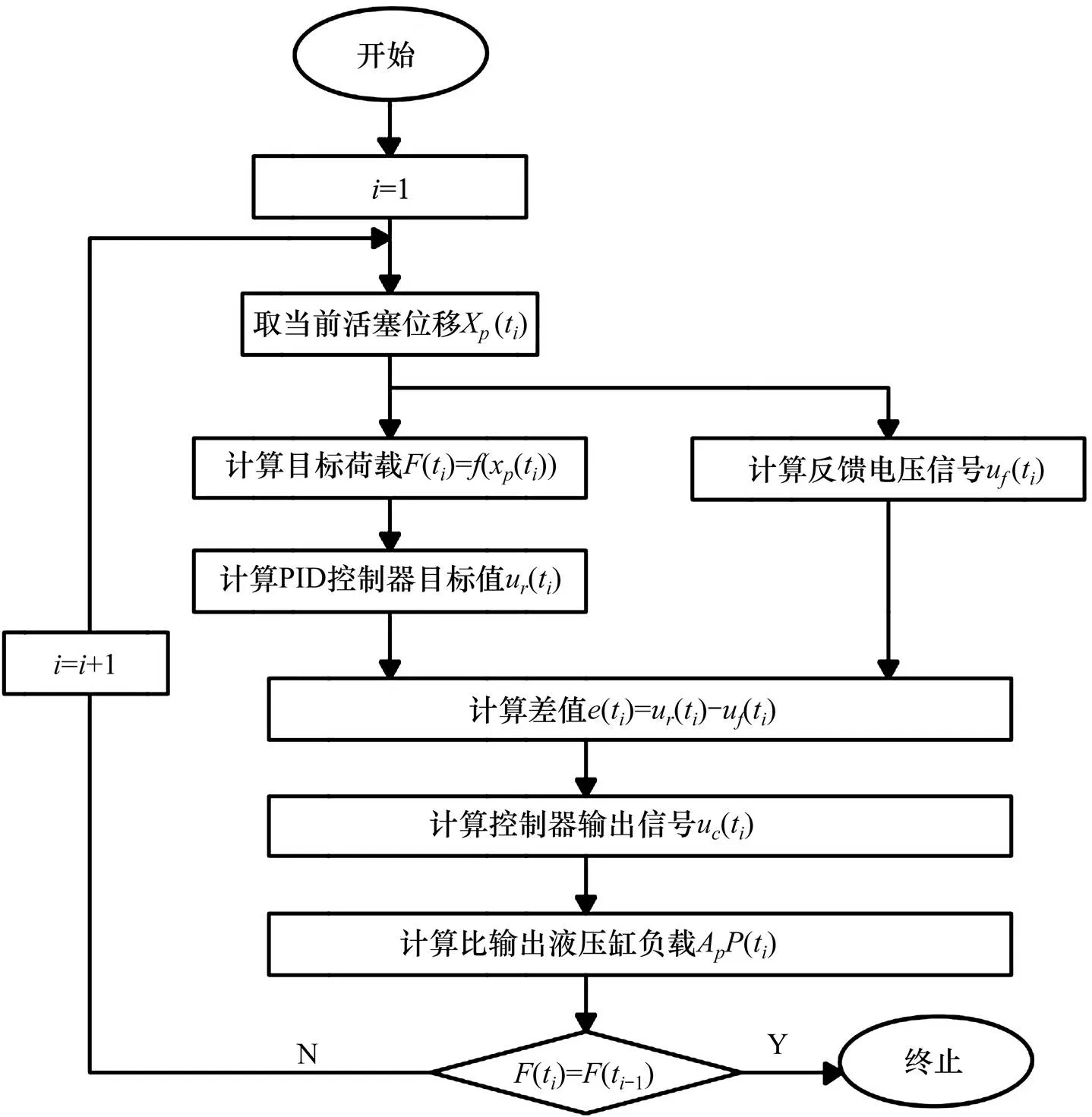
图4 控制流程
2.2.1 结构−液压系统直接相互作用
本文所设计加载系统的主要功能是模拟地层和盾构隧道之间相互作用。以下叙述这一功能的实现原理。
假定第号液压缸的负载力为F,活塞位移为x,对于结构而言,F是其节点荷载,x是其节点位移。由于在此系统中结构除受到24个液压缸所加荷载之外不再受到其他边界条件约束,所以,一旦结构所受荷载确定,则其各节点的位移将完全确定(可能相差刚体位移),反之,一旦结构各节点的位移确定,其所受荷载也将完全确定。所以,结构的节点位移和结构节点荷载之间是一一对应的,可以采用一矩阵进行表达,设此矩阵为,则结构节点位移和节点荷载的关系可以写为式(16):



其中第1个方程表征结构的受力性能,第2个方程表征地层的荷载位移曲线。以上分析表明,加载系统与试验结构相互作用的结果,一定是得出既满足结构受力性能,又满足加载系统内预置地层荷载位移曲线的液压缸负载和活塞行程,从而能够达到模拟实际工程中地层和隧道相互作用的目的。
2.2.2 多个液压缸的间接相互作用
当液压缸采用传统的荷载控制和位移控制时,24个液压缸彼此之间并无联系,完全按照各自预定的加载曲线进行加载,但采用荷载位移曲线控制的液压缸则不然。由于由荷载位移曲线控制的液压缸荷载由其行程决定,其行程等于加载点处结构的位移,而结构的位移实际上由所有液压缸的荷载决定,所以理论上每个液压缸的荷载都与其他液压缸有关。如下式,假设第号液压缸的荷载发生ΔF的变化,依据结构的刚度方程,如式(16)所示,第号液压缸处结构位移变化量为:
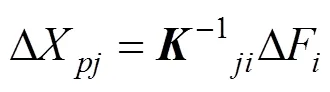

现在需要研究ΔF和ΔF之间的大小关系。如果由第号液压缸荷载变化ΔF引起的第号液压缸荷载变化ΔF<ΔF,则可以判断,第号液压缸荷载变化引起的系统波动将逐渐减小,系统最终趋于稳定。但是,如果ΔF>ΔF,则第号液压缸引起的系统波动将被逐次放大,系统最终趋于震荡。采用泰勒级数将式(19)展开,只保留第1项,可得 式(20):


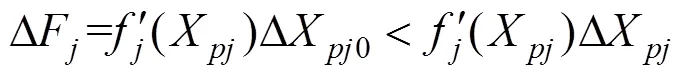

从而,考虑到结构和液压系统在响应时间上的不同,系统也将趋于稳定。
3 荷载位移曲线控制模式的试验应用
3.1 试验装置
本次试验的试验装置如图5。

图5 试验装置及液压缸编号
如图5所示,液压缸安装在钢环梁反力架上,每15° 1个,共24个。每个液压缸由一个比例换向阀控制,比例换向阀安装在反力架上不锈钢防水箱中,比例放大器集成在比例换向阀上,如图6所示。

图6 比例换向阀
所有比例换向阀均能够由控制室中的上位机(内置PID控制程序)进行压力闭环,位移闭环和压力位移闭环的控制。
2.1.2节所述位移传感器安装在液压缸缸筒上,所述力传感器安装在液压缸活塞杆头部。
3.2 试验构件
试验研究所采用的试件外直径为6.2 m,全环由1块封顶块(F)、2块邻接块(L1和L2)和3块标准块(B1,B2和B3)组成。管片厚度为0.35 m,环宽为1.5 m。衬砌圆环构造见图7。

图7 衬砌圆环构造
3.3 试验过程
1-24号液压缸首先采用荷载控制,分10级加载至静止土压力对应的荷载0。然后顶部和底部的7-12号液压缸,19-24号液压缸仍然采用荷载控制并保持荷载不变,其余液压缸改为荷载位移曲线控制,直至稳定。
3.4 实测液压缸荷载−时间曲线定性分析
3.4.1 试验结果预期
依据试验的加载过程,预期各液压缸的荷载−时间曲线将会呈现如下特征:在荷载控制阶段,各液压缸荷载呈现阶梯状增长,控制模式由荷载控制转化为荷载位移曲线控制之后,由于在前期加载过程中衬砌环呈现横鸭蛋变形,腰部产生指向地层的位移,所以此过程中腰部液压缸的荷载有所增长,且增长值与地层抗力值基本相当。
3.4.2 单个液压缸的试验结果
首先考察单个液压缸的荷载−行程曲线,以3号液压缸为例。第3号液压缸的荷载−行程曲线如图8中曲线所示。
由图8可知,单个液压缸的行为与试验前预期完全相符。试验开始后的第16~第20 h,所有液压缸按照荷载控制,分级等量地加载至静止土压力,而在这段时间,图示液压缸荷载呈阶梯状增长,与预期相符。
试验开始后的第30~40 h,腰部液压缸(以3号为代表)改为荷载位移曲线控制,由于腰部发生了朝向土层的位移,所受到的土压力从静止土压力向被动土压力发展,土压力增大。由图可知,这一阶段液压缸荷载增大,与预期相符。
3.4.3 多个液压缸相互作用的试验结果
选取第1号,第2号和第3号液压缸进行研究,其荷载−时间曲线如图8所示。

图8 多个液压缸相互作用
由图8可知,在试验未开始前,第1号,第2号,第3号液压缸的负载均维持在12.5 t左右。试验开始后,3个液压缸的负载呈阶梯状增长。第1号液压缸的负载分10级增加到22.9 t左右,第2号千斤顶负载分10级增加到20.4 t左右,第3号千斤顶的负载分10级增加到19 t左右。
在试验开始后的第36 h左右,腰部液压缸改为荷载位移曲线控制,由于前期腰部发生指向地层的位移,所以第1号,第2号,第3号液压缸荷载均大幅增加、第1号千斤顶的荷载增长达3.27 t,第2号千斤顶的荷载增长达4.8 t,第3号千斤顶的荷载增长达5.81 t,但并未出现各液压缸相互影响,荷载长期不稳定的情况。第1号千斤顶的负载很快稳定在26.17 t左右,第2号千斤顶的负载很快稳定在25.2 t左右,第3号千斤顶的负载很快稳定在 24.81 t左右。
3.5 实测液压缸荷载−时间曲线定量分析
由试验过程可知,在腰部液压缸的控制模式由荷载控制调整为荷载位移曲线控制之后,腰部液压缸的荷载均有明显增加。这是由于在前期加载中隧道腰部发生了朝向土体的变形。所以,这部分增加的荷载实际上代表传统盾构隧道设计中的地层抗力。而地层抗力可以通过基床系数乘以结构变形来进行估算。比较估算值和腰部液压缸荷载增量,可以验证本次试验中荷载位移曲线控制模式是否 准确。
选取腰部一侧的第1号~第6号液压缸进行研究。从试验开始到腰部液压缸切换到荷载位移曲线控制,1~6号液压缸的行程变化如表1所示。

表1 液压缸行程变化
由地勘报告可知,第4~6号液压缸对应位置基床系数为9 576 kN/m3,第1~3号液压缸对应位置基床系数为7559 kN/m3,所以,盾构隧道一侧腰部地基总抗力大小为30.6 t。
各液压缸荷载增量如表2所示。

表2 加载模式转换荷载增量
由表2可知,液压缸1~6在加载模式转换的过程中荷载增量一共为29.7 t。
荷载位移曲线控制模式施加的地层抗力与计算得到的地层抗力差距为2.9%,荷载位移曲线控制模式是准确的。
4 结论
1) 荷载位移曲线控制模式可以精确模拟盾构隧道所受荷载随结构变形而变化的特征,从而解决了传统盾构隧道足尺试验加载模式难以模拟地层对结构的真实作用的问题。具有良好的应用前景。
2) 在结构尚具有承载能力时,采用荷载位移曲线控制的各液压缸之间的相互作用有限,体系能较快地趋于稳定。
[1] 王如路, 宋博, 王祺, 等. 双圆盾构隧道衬砌错缝拼装整环试验及结构分析[J]. 地下工程与隧道, 2001(1): 12−15, 21, 47. WANG Rulu, SONG Bo, WANG Qi, et al. Lining experiment and structure analysis of bi-circular shield tunnel with staggered joint splice on segments[J]. Underground Engineering and Tunnels, 2001(1): 12−15, 21, 47.
[2] 曹文宏, 陈正杰, 杨志豪. 超大直径隧道衬砌足尺结构试验研究[J]. 市政技术, 2009, 27(增2): 239−242. CAO Wenhong, CHEN Zhengjie, YANG Zhihao. Experimental investigation of super large lining structure of tunnel in full size[J]. Municipal Engineering Technology, 2009, 27(Suppl 2): 239−242.
[3] 何川, 封坤, 苏宗贤. 大断面水下盾构隧道原型结构加载试验系统的研发与应用[J]. 岩石力学与工程学报, 2011, 30(2): 254−266. HE Chuan, FENG Kun, SU Songxian. Development and application of loading test system of prototype structure for underwater shield tunnel with large cross section[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(2): 254−266.
[4] Blom C B M. Design philosophy of concrete lining for tunnels in soft soils[D]. Delft, the Netherlands: Delft University Technology, 2002.
[5] Jorg S, Dieter W. Suitability tests for the lining for the 4th elbe tunnel tube-results of large-scale tests[J]. Tunnel, 2000(1): 34−44.
[6] 毕湘利, 柳献, 王秀志, 等. 通缝拼装盾构隧道结构极限承载力的足尺试验研究[J]. 土木工程学报, 2014, 47(10): 117−127. BI Xiangli, LIU Xian, WANG Xiuzhi, et al. Experimental investigation on the ultimate bearing capacity of continuous-jointed segmental tunnel linings[J]. Journal of Civil Engineering, 2014, 47(10): 117−127.
[7] 丁德云, 杨秀仁. 反应位移法抗震设计中地基弹簧系数取值的探讨[J]. 地震工程学报, 2016, 38(5): 685−692. DING Deyun, YANG Xiuren. Discussion on the spring constant of ground foundation in the seismic design of underground structures using the response displacement method[J]. China Earthquake Engineering Journal, 2016, 38(5): 685−692.
[8] 徐芝纶. 弹性力学简明教程[M]. 4版. 北京: 高等教育出版社, 2013. XU Zhilun. A concise course in elasticity[M]. 4th ed. Beijing: Higher Education Press, 2002.
[9] Verruijt A . Deformations of an elastic half plane with a circular cavity[J]. International Journal of Solids and Structures, 1998, 35(21): 2795–2804.
[10] 黄茂松, 曹杰. 隧道地震响应简化分析与动力离心试验验证[J]. 岩石力学与工程学报, 2010, 29(2): 271− 280. HUANG Maosong, CAO Jie. Simplified analysis of tunnel earthquake response and centrifuge modelling calibration[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(2): 254−266.
[11] 袁松, 王峥峥, 周佳媚. 隧道地震动力计算边界取值范围研究[J]. 土木工程学报, 2012, 45(11): 166−172. YUAN Song, WANG Zhengzheng, ZHOU Jiamei. Study on the model boundary determination in tunnel’s earthquake dynamic analysis[J]. Journal of Civil Engineering, 2012, 45(11): 166−172.
[12] 覃展斌, 陈飞飞, 金波, 等. 电液比例阀阀心位置控制PID自整定方法[J]. 浙江大学学报(工学版), 2015, 49(8): 1503−1508, 1528. QIN Zhanbin, CHEN Feifei, JIN Bo, et al. PID auto tuning method for spool position control of electro hydraulic proportional valve[J]. Journal of Zhejiang University, 2015, 49(8): 1503−1508, 1528.
Design and application of a hydraulic loading system simulating tunnel-soil interaction
ZHU Yaohong1, YANG Zhenhua2, CHEN Feifei3, LIU Xian2
(1. Faculty of Architectural, Civil Engineering and Environment, Ningbo University, Ningbo 315211, China; 2. Department of Geotechnical Engineer, Tongji University, Shanghai 200092, China;3. Ningbo Hoyea Machinery Manufacture Co., Ltd, Ningbo 315131, China)
The full-scale test of shield tunnels mainly adopts load control as load pattern at present. The load applied on the structure by the hydraulic system is derived from the calculated value of the static earth pressure. This loading method adopts the idea of load structure method, and it is difficult to reflect the characteristics of the earth pressure acting on the shield tunnel as the structure deforms. To solve this problem, the principle of a control mode named load-displacement control subsystem is proposed and it has been used in a full-scale test. First obtain the functional relationship between the stratum displacement and the earth pressure. Then observe the relative position of this curve and the point taking the hydraulic cylinder top force and stroke as coordinates, and adjust the jacking force and make it obey the functional relationship. This control subsystem can simulate the characteristic that the load on an underground structure will change when it deform. And there should be good prospective.
structural experiment; loading system; load-displacement control subsystem
U45
A
1672 − 7029(2020)04 − 0915 − 09
10.19713/j.cnki.43−1423/u.T20190526
2019−06−14
国家重点研发资助计划项目(2017YFC0805004)
柳献(1977 −),男,湖北武汉人,教授,博士,从事隧道与地下建筑结构研究;E−mail:xian.liu@tongji.edu.cn
(编辑 阳丽霞)

