高速铁路连续梁桥全寿命周期概率地震损失分析

冯莉，樊燕燕，李子奇, 2，王力

高速铁路连续梁桥全寿命周期概率地震损失分析

冯莉1，樊燕燕1，李子奇1, 2，王力1

(1. 兰州交通大学 土木工程学院，甘肃 兰州 730070；2. 兰州交通大学 道桥灾害防治技术国家地方联合实验室，甘肃 兰州 730070)

在全概率 PBEE方法(PEER-PBEE Methodology)的基础上，建立桥梁结构全寿命周期地震损失计算方法和分析流程。以一座高速铁路连续梁桥为背景，通过地震易损性和地震危险性的卷积确定结构的地震风险概率，最终得到桥梁结构全寿命周期地震损失。研究结果表明：该高速铁路连续梁桥在寿命周期内发生轻微损伤和中等损伤的概率较大，其造成的损失约占全部地震损失的70%；桥梁系统寿命周期震害损失与资金折现率有关，占结构初始成本的1.91%~4.38%；本文研究结果对高速铁路桥梁结构的地震经济损失计算方法和地震巨灾保险的未来推广具有借鉴意义。

地震危险性；地震易损性；地震风险；全寿命周期地震损失；数值积分法

高速铁路建设中为节约土地资源，大量采用“以桥代路”策略以保证高速列车运行的安全性和舒适性。因此，桥梁在高速铁路线上占比通常较大。我国地震频发，很多高速铁路桥梁位于地震频发区，一旦发生强烈地震，势必会给经济带来不可估量的损失。以往研究主要聚焦于桥梁在地震作用下的受力性能，而对其在全寿命周期内的地震损失研究极少。地震经济损失评估作为地震风险分析的重要构成部分，是相关部门制定防震减灾政策及厘定保险费率重要依据。评估桥梁全寿命周期地震损失要考虑结构所在场地地震危险性、基于性能的损伤程度、维修损失估计等多方面内容，较结构抗震力学性能分析更为复杂。目前，我国在工程全寿命期地震灾害损失方面的应用基础研究仍处于探索阶段。地震损失成本评估是桥梁结构全寿命周期成本分析必须考虑的问题，也是基于全寿命理念的桥梁结构抗震设计方法的关键。国外对于工程结构的全寿命周期地震损失研究开始较早。LIU等[1]通过计算节能建筑由地震损伤带来的未来成本，运用寿命周期成本(LCC)分析方法来评价建筑节能特性的长期成本效益。El-Din等[2]将一导管架型海洋平台简化为等效单自由度系统，采用近似易损性曲线，对其全生命周期地震损失进行分析，并且与多自由度系统进行对比，验证了简化计算方法的准确度，可用于地震损失初步评估。Ramirez等[3]对所选取的30栋美国加州地震高烈度地区的办公楼样本采用基于性能的地震工程分析流程计算了地震年预期损失和全寿命周期地震成本损失。Castaldo等[4]分析采用不同隔震周期的单凹FPS支座隔震系统生命周期成本，同时考虑了整个结构在寿命周期(50年)内的初始成本和预期损失成本，以评估隔震度对隔震性能和总造价的影响。我国在工程全寿命周期地震损失方面的应用基础研究还处于起步阶段[5]。唐玉等[6]对我国抗震规范中的3级设防水准作出了进一步的5级划分，近似分析了结构在各级性能水平下的失效概率，构建了基于“投资—效益”准则的结构全寿命周期费用的计算模型。朱健等[7]采用增量动力分析对我国西部地区的单层钢混排架工业厂房采用CFRP加固前后的地震损伤和全寿命周期地震损失进行对比计算分析，结果表明采用CFRP加固技术后的厂房具有更好的全寿命周期地震损失经济性。目前，国内对于地震经济损失的研究大多集中于建筑结构，而针对铁路桥梁的地震损失研究相对匮乏且多数基于统计经验性方法，只能对地震损失成本进行粗略的估算。美国太平洋地震工程研究中心(PEER)基于性能的地震工程理论(PBEE)将地震损失和地震风险作为性能目标，采用全概率理论对工程结构的抗震性能进行评估[8]。全寿命周期地震损失评估作为PEER-PBEE理论的延续，对基于全寿命周期的桥梁结构抗震设计方案的选择具有重要意义。在此，本文以一座高速铁路连续梁桥为工程背景，基于增量动力分析结果对该桥进行地震易损性分析，将地震危险性和地震易损性相结合来确定桥梁地震风险概率，评估结构全寿命周期地震损失。

1 桥梁全寿命周期地震损失评估方法

PBEE理论将基于概率的抗震性能评估分解为4个部分：场地危险性分析、需求分析、损伤分析和损失分析。为了使业主、利益相关者更好理解结构的抗震性能及风险，桥梁结构全寿命周期地震损失用货币价值评估结构在一定时间内发生不同强度地震造成的风险后果，可以表达为[2]：

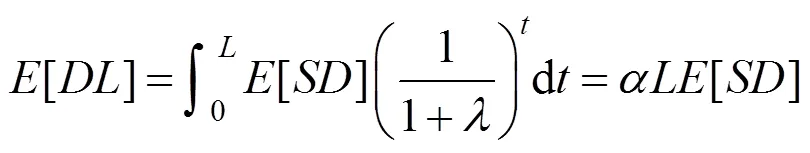
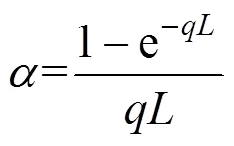
假定不考虑桥梁结构的时变特性，且结构在每次发生损伤后，都会立即修复至原始状态。综合考虑桥梁结构可能遭受的所有损伤状态及其所造成的损失，将桥梁结构地震年预期损失[]表示为：

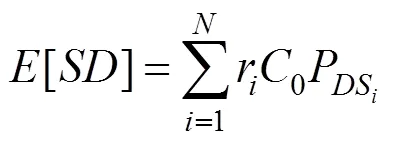
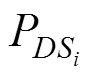
《地震现场工作第4部分：灾害直接损失评估》[9]中将结构损伤状态划分为基本完好、轻微损伤、中等损伤、严重损伤和完全破坏5个等级，并且给出了各损伤状态对应的损失比r的建议值。结合我国经济发展水平，对桥梁结构各损伤状态下的损失比按表1取值。由于结构一旦发生严重损伤，修复难度极大，故将严重损伤状态下的损失值取为1.0。

表1 桥梁结构各损伤状态及损失比ri

2 基于概率的地震风险评估理论

基于概率的地震风险研究的关键是定量确定地震作用和结构中存在的不确定性。由地震风险定义知：结构的地震风险=地震危险性×地震易损性。

2.1 地震危险性

地震危险性表示某一场地发生超过某一强度地震的年平均概率，可用简化的幂指数地震危险性概率模型近似表达[10]：

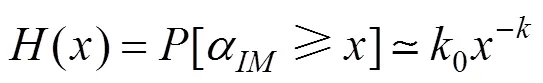
式中：0和为地震危险性曲线的形状参数，分别由式(4)~(5)确定。

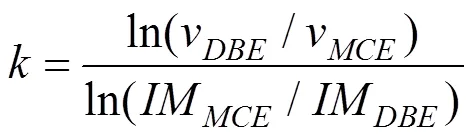
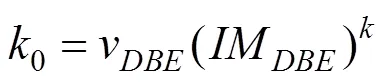
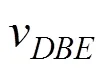
2.2 地震易损性

地震易损性表示给定地震动强度下结构或构件的地震响应超过极限状态的条件失效超越概率。与传统确定性方法相比，地震易损性分析可以更加全面客观地评价桥梁结构在寿命周期内遭受不同强度地震下损伤的可能性。考虑结构和地震动不确定性的地震易损性函数如式[11](6)所示：

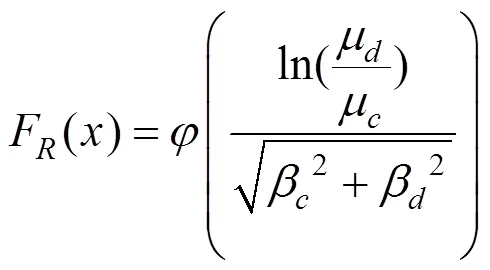
选取合适的结构破坏模式和破坏指标，对IDA法得到的结构关键截面一系列地震响应值进行线性拟合后，依式(6)绘制出易损性曲线。

2.3 桥梁地震风险表达式

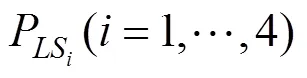
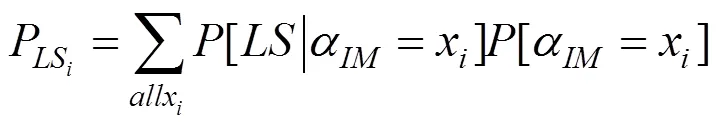
式中：为地震动强度参数，实际地震动是连续的，利用地震危险性和地震易损性的卷积，将式(3)写成连续形式：

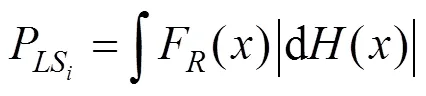
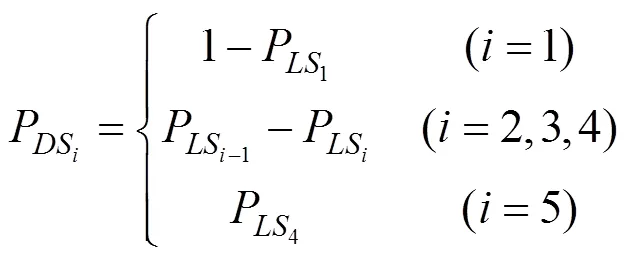
1) 数值积分解

为了简化数值积分计算，根据文献[14]对易损性曲线进行简单函数拟合：

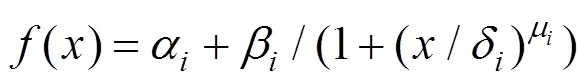
式中：α，β，δ和μ均为待定参数；为地震峰值加速度。

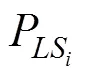
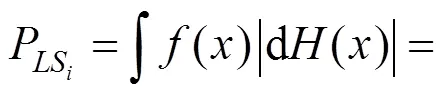
2) 解析解

Vamvatsikos等[13]将地震易损性函数和地震危险性函数代入式(8)，得到了如式(12)所示的概率地震风险函数的解析表达式：

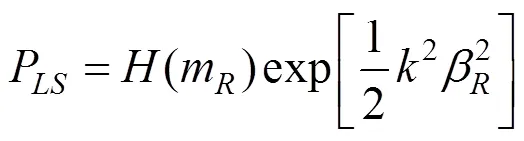
式中：(m)为在能力中位值m处的地震危险；由地震危险性曲线确定；m和为易损性函数的参数，分别由式(13)和式(14)确定：

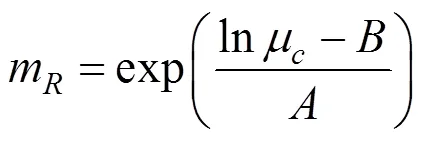
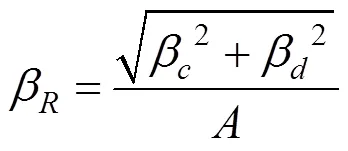
则式(12)可用式(15)表达：

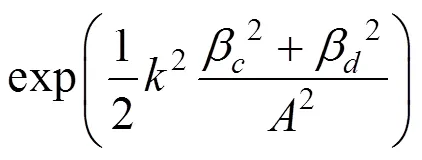
3 寿命周期概率地震损失分析流程

结合地震危险性分析、地震易损性分析和地震损失估计，可以计算桥梁结构寿命周期概率地震损失。分析流程如图1所示。

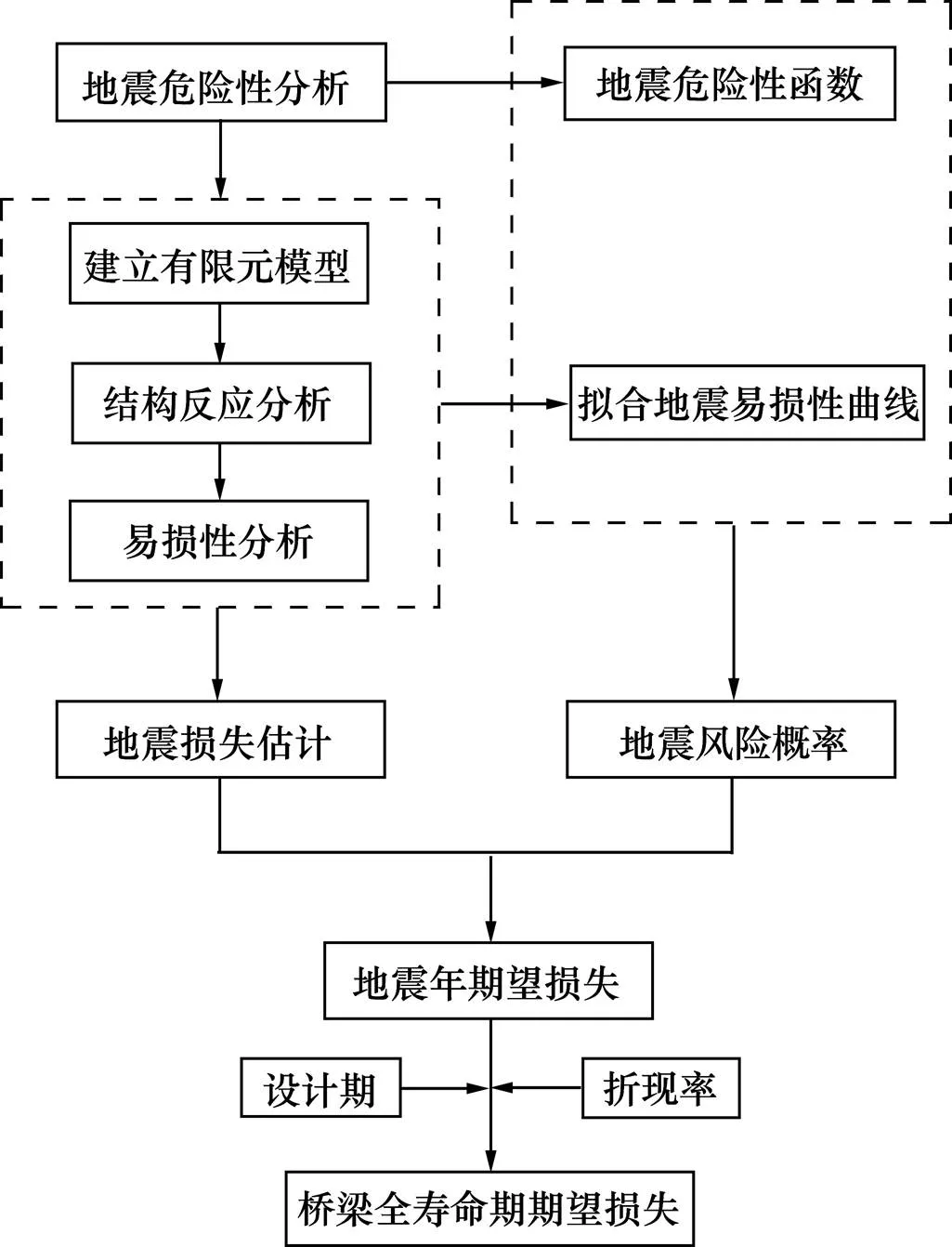
图1 桥梁寿命周期概率地震损失分析流程

4 算例分析

4.1 工程概况及有限元模型

本文以兰新二线上一座(40+64+40) m的高速铁路连续梁桥为算例，该桥总造价712.8万元。采用MIDAS/Civil建立全桥非线性有限元模型(见图2)。其中，主梁采用C50混凝土，为单箱单室变截面、变高度结构，箱梁底板按二次抛物线变化，运用梁单元模拟；桥墩采用C30混凝土，所有桥墩均用弹塑性纤维单元模拟(见图3)，其中，桥墩混凝土采用Kent-Park模型模拟，桥墩主筋采用双折线模型模拟；支座采用球形钢支座，通过竖向刚臂连接支座，刚臂上端与主梁节点刚性主从连接，下端为支座底端节点，与墩顶节点刚性主从连接。为了简化计算，不考虑桩−土相互作用的影响，即承台底固结。

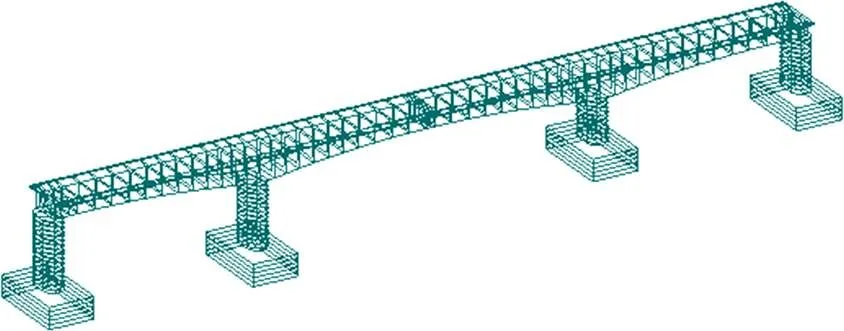
图2 全桥有限元模型

图3 桥墩纤维截面

4.2 地震危险性分析

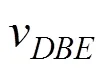
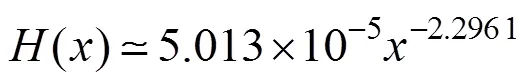
4.3 损伤指标确定及损伤状态划分

大量震害表明，桥墩、支座破坏都有可能导致桥梁结构系统失效，故本文考虑桥墩、支座的破坏形式，用系统易损性曲线评估桥梁结构的抗震性能。宋帅等[16]采用相对位移延性比来定义支座的损伤状态, 即定义各极限状态支座允许相对位移与剪切应变等于100%时的支座相对位移之比为支座相对位移延性比。何浩祥等[17]考虑到传统的桥梁易损性分析中只采用典型桥墩的曲率或位移阈值作为损伤参量，不能充分反映滞回耗能能力，进而提出基于弹塑性耗能差率的桥墩损伤评价方法。本文桥例中活动支座容许位移为100 mm。参考以上文献结合伸缩缝处碰撞特点和能量损伤指数，定义支座和桥墩不同损伤等级的分界点，如表2所示。

表2 损伤指标范围

4.4 易损性分析

从PEER选取与桥址处场地条件近似的20条实际地震动记录作为地震输入，对该桥进行增量动力分析。以地震峰值加速度(PGA)作为地震动强度参数，以0.05为步长对逐条地震波从0~1.0等步长调幅，获得桥墩和支座的结构响应。最后，将计算结果结合结构各级损伤状态，再通过式(6)绘制出支座和桥墩的地震易损性曲线，见图4和图5。

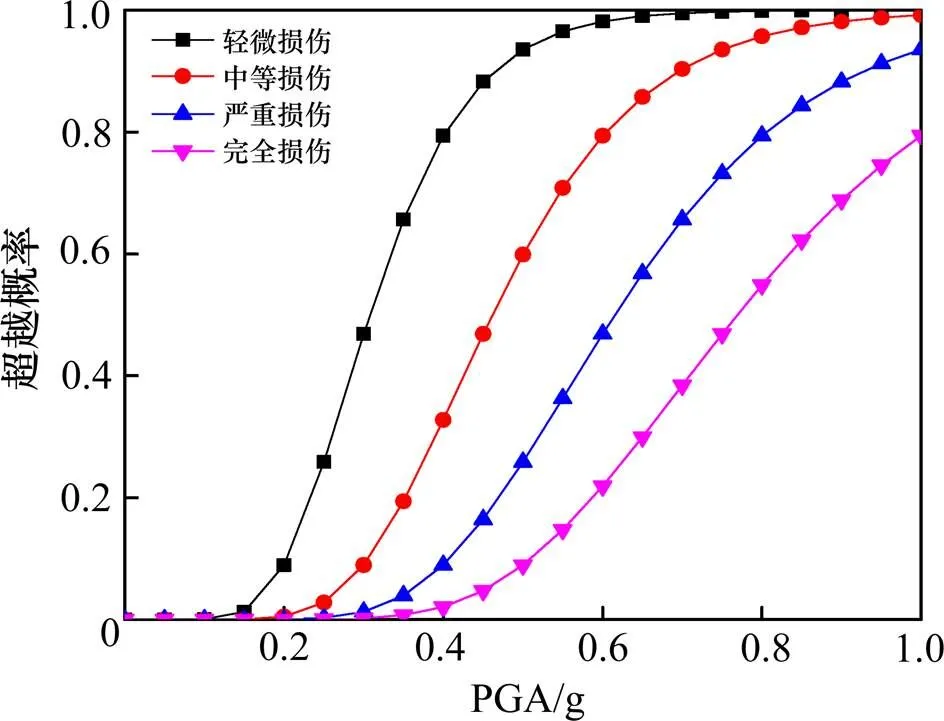
图4 支座易损性曲线

为简化计算，本文假定易损性构件的损伤状况相互独立，采用一阶可靠度理论进行桥梁系统的地震易损性分析，认定桥梁结构的可靠度体系属于串联体系，即一旦结构任意构件达到极限状态则认为桥梁系统达到极限状态，系统易损性计算式[11]如下：

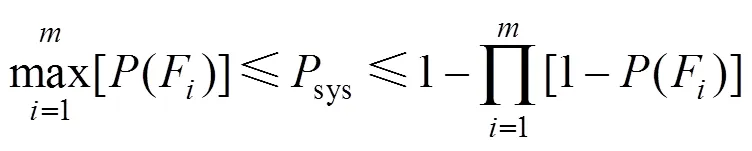
式中：为桥梁系统达到某一损伤状态的超越概率；为第i个构件达到某一损伤状态的超越概率。

根据式(17)，计算桥梁系统超过各损伤状态的失效概率，绘制地震易损性曲线(见图6)。

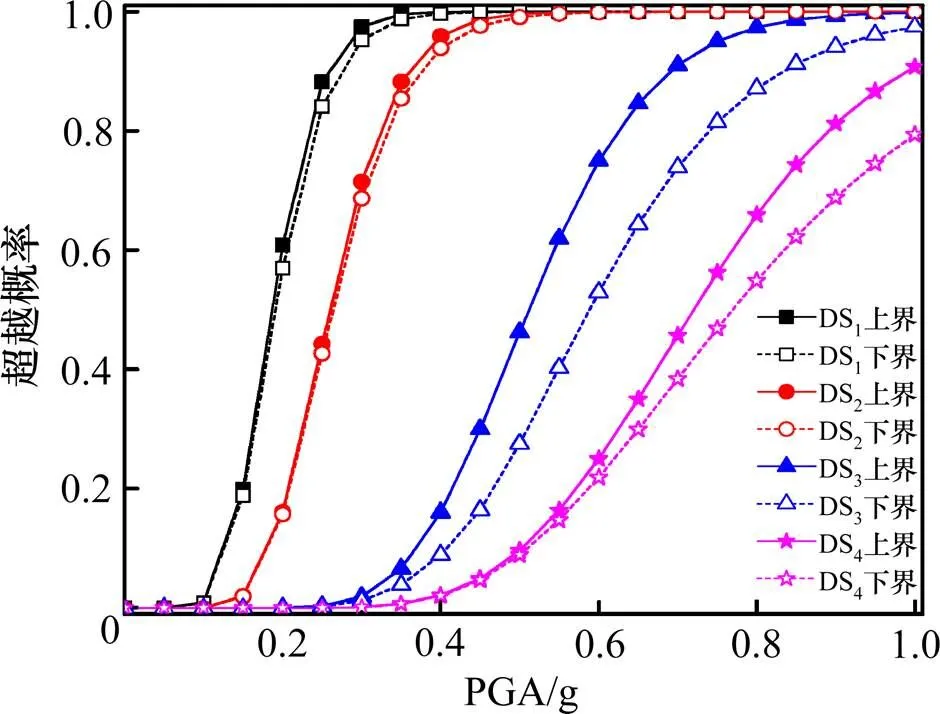
图6 桥梁系统地震易损性曲线

4.5 桥梁地震损失计算

4.5.1 地震风险概率

用解析解法进行地震风险计算时，由桥墩构件代替桥梁系统易损性，根据式(13)~(14)求得桥墩易损性函数的参数m和，计算结果如表3所示。运用数值积分法进行地震风险计算，将桥墩构件和桥梁系统易损性曲线通过式(10)拟合为简单函数，结构各损伤状态拟合参数如表4所示。

表3 桥墩易损性函数参数

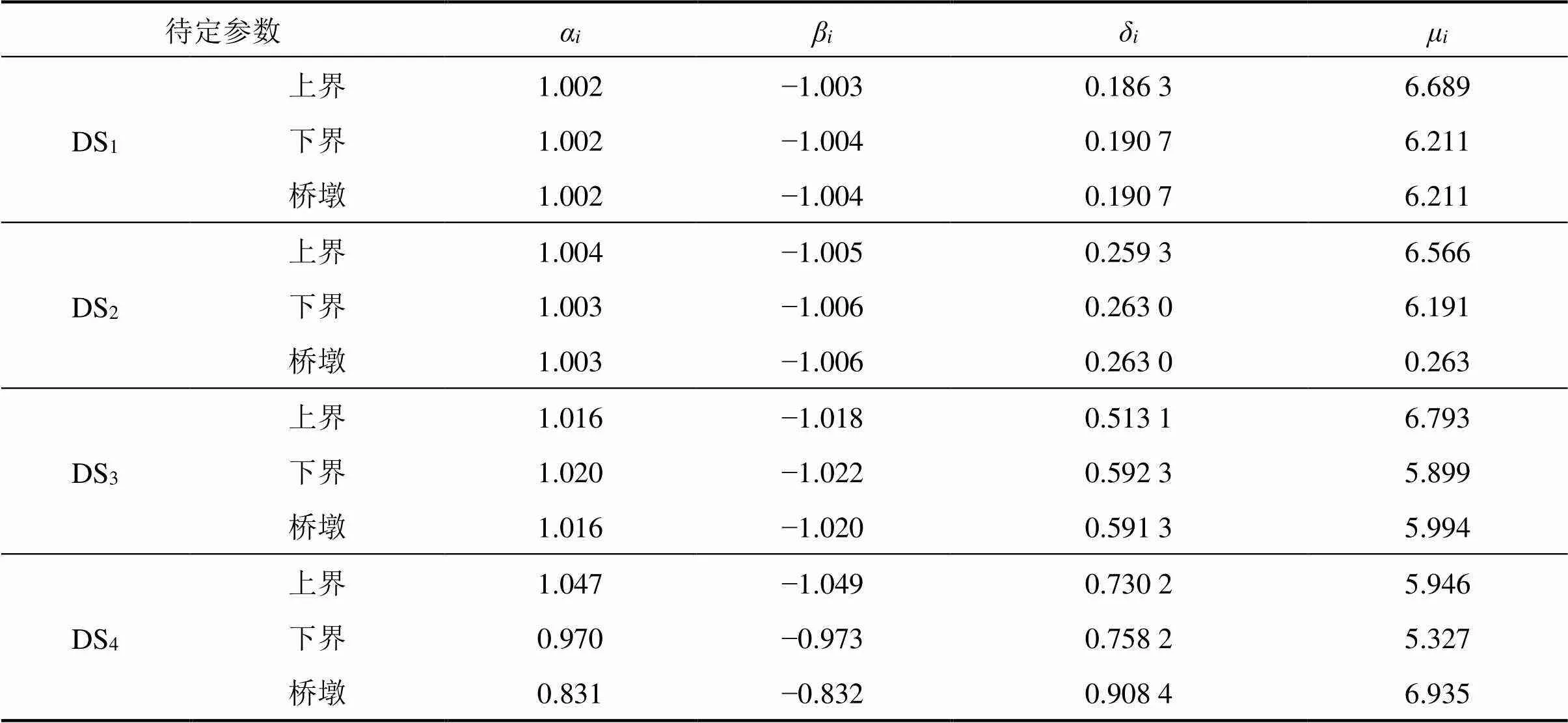
表4 易损性曲线拟合参数

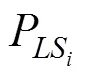
表5 桥梁年平均失效概率

由表4可知：1) 若取一阶界限法的上界作为系统的地震年平均失效概率值，则桥梁系统年平均失效概率基本大于桥墩构件的年平均失效概率，因此，仅用桥墩构件代替全桥会低估该桥地震风险。2) 分别用解析解和数值解计算桥墩地震风险概率，DS2，DS3和DS4的年失效概率均为数值解大于解析解，DS5则是解析解大于数值解。桥墩DS2，DS3和DS4的失效概率数值解更接近于系统上界，相对误差分别为0%，3.7%和7.8%。相对而言，桥墩DS4和DS5的失效概率解析解与系统上界更接近，二者相对误差分别为5.5%和34.5%。

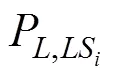
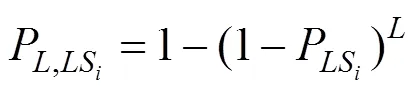
表6 桥梁寿命期(100 a)地震超越概率

由表6可知，该桥在寿命周期内发生轻微损伤、中等损伤和严重损伤的风险概率上界分别为24.45%，12.20%和2.12%。根据桥址地震危险性和《铁路工程抗震设计规范》，该桥设防水准目标可通过概率形式表达为：100 a内多遇地震作用下发生轻微损伤的超越概率为86.7%，设计地震作用下发生中等损伤的超越概率为18.9%，罕遇地震作用下发生严重损伤的超越概率为3.9%。综上，各损伤状态的风险概率均满足设防要求。

4.5.2 地震损失计算

根据桥梁年平均失效概率和损失比，由式(2)计算得到桥梁年预期地震损失(见表7)。

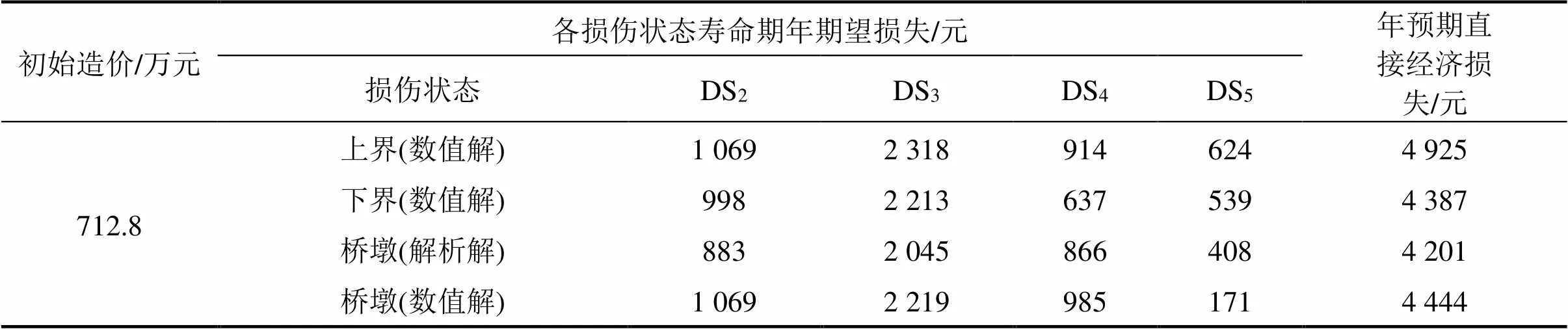
表7 桥梁全寿命周期年预期地震损失

由表7可以看出：1) 对比年预期地震直接经济损失值发现，桥梁系统上界＞桥墩数值解＞桥梁系统下界＞桥墩解析解。2) 虽然桥墩解析解较系统上界年预期地震直接损失有一定误差，但该方法较数值积分法省去了易损性函数拟合等复杂步骤，计算效率明显提高。因此，桥墩构件解析解对于桥梁结构地震损失的初步评估具有一定的优越性。

高速铁路桥梁寿命周期通常较长，故资金的时间价值对其全寿命周期地震损失评估的影响不可忽略。考虑折现率对桥梁全寿命周期地震损失的影响，选取折现率为1%，2%和3%分别按式(1)计算桥梁系统全寿命周期地震预期直接经济损失，计算结果如图7所示。

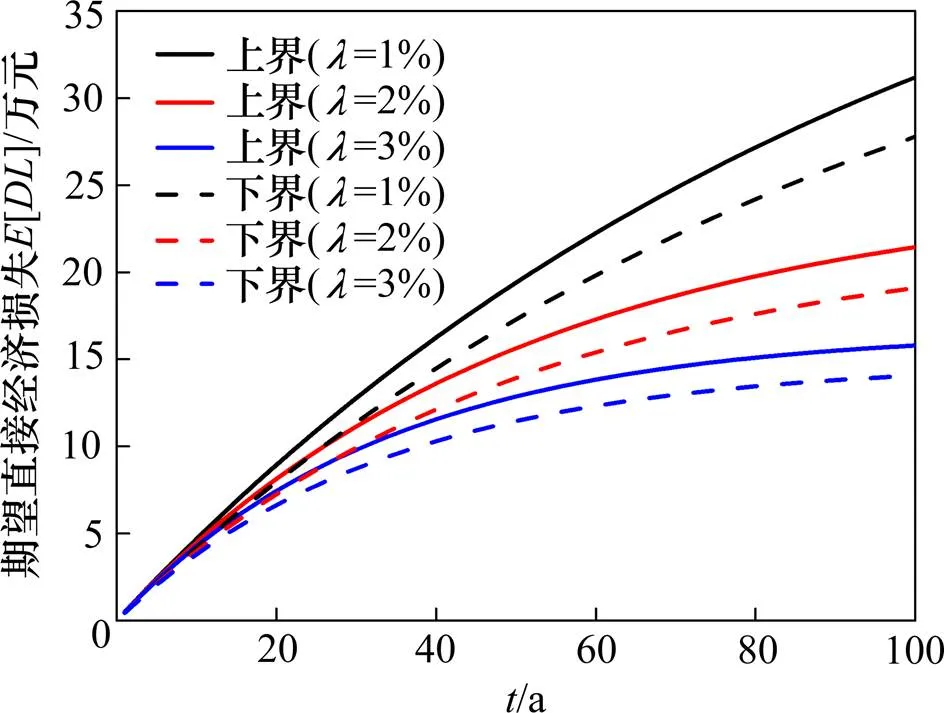
图7 桥梁期望直接经济损失

由图7可以看出：1) 桥梁寿命周期内由地震引起的期望直接经济损失最大值为31.2万元，占桥梁初始造价的4.38%；2) 折现率对于桥梁全寿命周期地震预期损失的影响较大，因此在结构寿命周期震害损失评估中，应根据社会经济发展状况，合理考虑资金的时间价值。

5 结论

1) 该桥梁在寿命周期内发生轻微损伤和中等损伤的概率较大，发生严重损伤和完全破坏的概率极小。由轻微损伤和中等损伤造成的损失约占全部损失的70%。桥梁全寿命周期内地震期望直接经济损失(系统上界)为31.2万元，占桥梁初始造价的4.38%。

2) 分别以数值积分和解析函数的方法确定结构的地震风险概率，相对于数值积分法，解析解法计算结果偏于保守，但计算效率更高，因此对桥梁地震损失的初步评价更显优越性。

3) 选取不同的折现率对桥梁结构全寿命周期地震损失的影响较大，震害损失评估中应根据社会经济发展水平合理地考量资金的时间价值。

4) 本文从概率角度客观评价桥梁寿命期地震损失，为桥梁抗震防灾及设计期经济性能评价提供理论基础，也可以为厘定地震保险费率提供依据。

[1] LIU Min, MI Baoxia. Life cycle cost analysis of energy-effificient buildings subjected to earthquakes[J]. Energy and Buildings, 2017(154): 581−589.

[2] El-Din M N, Kim J. Simplified seismic life cycle cost estimation of a steel jacket offshore platform structure[J]. Structure and Infrastructure Engineering, 2016: 1−18.

[3] Ramirez C M, Liel A B, Mitrani-Reiser J, et al. Expected earthquake damage and repair costs in reinforced concrete frame buildings[J]. Earthquake Engineering & Structural Dynamics, 2012, 41(11): 1455−1475.

[4] Castaldo P, Palazzo B, Della Vecchia P. Life-cycle cost and seismic reliability analysis of 3D systems equipped with FPS for different isolation degrees[J]. Engineering Structures, 2016(125): 349−363.

[5] 朱健, 谭平, 周福霖, 等. 土木工程结构全寿命期地震损失成本进展研究[J]. 振动与冲击, 2015, 34(17): 111− 119. ZHU Jian, TAN Ping, ZHOU Fulin, et al. A review of study on life-cycle seismic loss estimation in civil engineering[J]. Journal of Vibration and Shock, 2015, 34(17): 111−119.

[6] 唐玉, 郑七振, 楼梦麟. 基于“投资―效益”准则的结构全寿命总费用模型[J]. 地震工程与工程振动, 2012, 32(4): 188−194. TANG Yu, ZHENG Qizhen, LOU Menglin. A modified structural life-time cost model based on the cost-effectiveness criterion[J]. Earthquake Engineering and Engineering Dynamics, 2012, 32(4): 188−194.

[7] 朱健, 赵均海, 谭平, 等. 基于CFRP加固的钢混排架厂房全寿命周期地震成本研究[J]. 工程力学, 2019, 36(2): 141−153. ZHU Jian, ZHAO Junhai, TAN Ping, et al. Ceismic life-cycle loss estimation of CFRP reinforced industrial buildings[J]. Engineering Mechanics, 2019, 36(2): 141− 153.

[8] Günay, Selim, Mosalam K M. PEER performance-based earthquake engineering methodology, revisited[J]. Journal of Earthquake Engineering, 2013, 17(6): 829− 858.

[9] GB/T 18208.4—2011, 地震现场工作第4部分: 灾害直接损失评估[S]. GB/T 18208.4—2011, the earthquake field work in fourthparts:the direct disaster loss assessment[S].

[10] Cornell C A, Jalayer F, Hamburger R O, et al. Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines[J]. Journal of Structural Engineering, 2002, 128(4): 526− 533.

[11] 郑凯锋, 陈力波, 庄卫林, 等. 基于概率性地震需求模型的桥梁易损性分析[J]. 工程力学, 2013, 30(5): 165− 171, 187. ZHENG Kaifeng, CHEN Libo, ZHUANG Weilin, et al. Bridge vulnerability analysis based on probabilistic seismic[J]. Engineering Mechanics, 2013, 30(5): 165− 171, 187.

[12] 吕大刚, 于晓辉, 王光远. 基于地震易损性解析函数的概率地震风险理论研究[J]. 建筑结构学报, 2013, 34(10): 41−48. LÜ Dagang, YU Xiaohui, WANG Guangyuan. Theoretical study of probabilistic seismic risk assessment based on analytical functions of seismic fragility[J]. Journal of Building Structures, 2013, 34(10): 41−48.

[13] Vamvatsikos D, Cornell C A. Applied incremental dynamic analysis[J]. Earthquake Spectra, 2012, 20(2): 491–514.

[14] 沈怀至. 基于性能的混凝土坝—地基系统地震破损分析与风险评价[D]. 北京: 清华大学, 2007. SHEN Huaizhi. Performance-based seismic damage analysis and risk evaluation model for concrete dam- foundation system[D]. Beijing:Tsinghua University, 2007.

[15] GB 50111—2006, 铁路工程抗震设计规范[S]. GB 50111—2006, Code for seismic design of railway engineering[S].

[16] 宋帅, 钱永久, 吴刚. 基于多元Copula函数的桥梁体系地震易损性分析方法研究[J]. 振动与冲击, 2017, 36(9): 122−129, 208. SONG Shuai, QIAN Yongjiu, WU Gang. Seismic fragility analysis of a bridge system based on multivariate Copula function[J]. Journal of Vibration and Shock, 2017, 36(9):122−129, 208.

[17] 何浩祥, 李瑞峰, 闫维明. 基于多元模糊评定的桥梁综合地震易损性分析[J]. 振动工程学报, 2017, 30(2): 270−279. HE Haoxiang, LI Ruifeng,YAN Weiming. Bridge seismic fragility analysis method based on multiple fuzzy evaluation[J]. Journal of Vibration Engineering, 2017, 30(2): 270−279.

Probabilistic whole life cycle seismic loss analysis of high-speed railway continuous girder bridge

FENG Li1, FAN Yanyan1, LI Ziqi1, 2, WANG Li1

(1. School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China;2. National and Provincial Joint Engineering Laboratory of Road & Bridge Disaster Prevention and Control,Lanzhou Jiaotong University, Lanzhou 730070, China)

The calculation method and analysis flow of seismic loss in the whole life cycle of bridge structures are established based on the PEER-PBEE Methodology. Under the background of a high-speed railway continuous beam bridge, based on convolution of seismic vulnerability and seismic risk, the probabilistic seismic risk of the structure is determined. Finally, the seismic loss of the whole life cycle of the bridge is obtained. The results show that the high-speed railway continuous beam bridge has a high probability of minor damage and moderate damage in the whole life cycle, and the loss is about 70% of the total loss. The damage loss of bridge system life cycle is related to the discount rate of funds, which is 1.91%~4.49% of the initial cost of the structure. The results of this paper can be used for reference to the calculation method of earthquake economic loss of high-speed railway bridge structure and the extension of earthquake catastrophe insurance in the future.

seismic risk; seismic vulnerability; probabilistic seismic risk; life cycle seismic loss; numerical integrating

U24；P315.9

A

1672 − 7029(2020)04 − 0815 − 08

10.19713/j.cnki.43−1423/u.T20190690

2019−08−02

国家自然科学基金资助项目(51768037)；长江学者和创新团队发展计划滚动支持项目(IRT15R29)

樊燕燕(1976−)，女，河南禹州人，副教授，从事桥梁结构风险评估理论研究；E−mail：12062481@qq.com

(编辑 阳丽霞)