高速公路出行距离特征分析与应用
崔洪军, 任志笑, 朱敏清, 王子鹏, 何美美
(1.河北工业大学土木与交通学院,天津 300401;2.河北锐驰交通工程咨询有限公司,石家庄 050051;3.北京交通大学交通运输学院,北京 100044)
随着高速公路里程数和交通量的不断增加,准确获取不同车型的出行距离特征以及起讫点(origin-destination, OD)矩阵对于管理者制定相应管理措施和规划方案十分重要。自高速公路联网收费政策实行以来,已经积累大量收费数据,如何充分利用收费数据挖掘车辆出行的潜在规律成为管理者和科研人员关注的焦点。
中外许多学者对出行距离特征分析和OD估算方法已有较多的研究,传统的出行距离特征提取主要通过不同交通方式距离衰减规律来体现[1-2]。针对出行距离特征,陈卓等[3]根据福建省高速公路OD矩阵数据,利用控模型法和空间分析法探寻距离衰减规律的空间分异特性。柯文前等[4]以江苏省高速公路流数据为基础,探寻城市间的空间关联特征和演化规律。针对OD估算模型的研究已基本成熟。崔洪军等[5]将出行特征与OD矩阵进行结合,利用居民出行调查数据分析城市交通小区居民出行时耗特征并建立OD估算模型。Wang等[6]、王海燕等[7]和梁超等[8]分别根据获取到的高速路网道路观测信息(断面交通量)、根据历史收费站转向比例数据和高速公路出入口明细表数据建立了OD矩阵估算模型,并根据不同迭代方法提高OD矩阵精度,但是上述方法未充分考虑不同车型出行特征,由于算法存在求解过程比较复杂、需要的数据量较大和计算结果精度不够[9-10]等问题,且后两者模型只适用于已建高速,对于新建高速推算的结果精度不高。
因此,根据中国高速公路全封闭收费公路特性和河北省内收费数据与主线收费站OD调查数据,充分分析高速公路各车型出行距离特征,利用空模型法模拟不同车型衰减规律,根据高速公路车辆出行特征与区域间的联系强度,建立一种基于收费站出入口断面流量数据的OD估算模型。模型充分利用收费数据,克服现有OD估算方法的计算复杂的缺点,在分析过程中不需要完整的OD矩阵,推导过程简单,有效减少管理人员工作量。
1 车辆出行距离特征
1.1 基础数据处理
为探寻不同车型出行规律,基础数据由河北省高速交通管理局采集2017年河北省高速公路分车型交通量报表,共计2 000余万条记录,分布范围从河北省北部张家口地区到南部邯郸地区。利用目前河北省高速收费标准明细表中收费车型分类标准和《公路工程技术标准》(JTGB01—2014)[11]中车型分类和折算系数,对数据进行分类汇总。车型分类为小客车、中型车、货车、汽车列车。由于根据主线收费站作为车辆起讫点则无法确定行经车辆完整的行驶路径,故而对整体数据产生影响,造成短距离车辆增加,使得出行分布规律不准确。针对此情况,通过对主线收费站进行OD调查,根据行经主线收费站车辆出行分布规律对主线站收费数据进行处理,其中距离矩阵通过地理信息系统(geographic information system,GIS)中路径搜索获取。
1.2 出行距离函数拟合及检验
1.2.1 分车型出行规律分析

图1 小客车出行距离与出行比例曲线Fig.1 The travel distance and travel proportion curve of passenger car

图2 中型车出行距离与出行比例曲线Fig.2 The travel distance and travel proportion curve of medium car

图3 货车出行比例与出行比例曲线Fig.3 The travel distance and travel proportion curve of large truck
对汇总后的分车型流量数据利用距离矩阵进行频数统计,频率直方图近似为正态分布和对数正态分布。因此,对4种车型出行分布规律分别用正态分布、对数正态分布进行函数拟合,图1~图4、表1所示为拟合结果,拟合效果采用R2(R-square)和和方差(the sum of squares due to error,SSE)指标来衡量。通过拟合结果可知,4种车型中小客车和中型车对数正态分布的R2均大于正态分布,对数正态分布SSE也均小于正态分布,因此对数正态分布拟合效果最好;同理,大货车和汽车列车正态分布拟合效果最好,其中出行距离均值分别为143、215、235、252 km。小客车中7座以下私家车占比较多,中型车主要包含大于19座的长途客车和载重大于2 t小于7 t的小货车,出行距离分别集中在50~150 km和50~250 km,两者以中短途出行形式为主,因此河北省内省域长途客车最佳营运距离为250 km;而货车和汽车列车大多都为载质量7 t以上货车,出行距离分布集中在100~250 km和150~300 km,长途出行居多,货车由于高速公路计重收费政策、出行成本、所载货物等因素的制约,导致其出行距离大于公路运输的经济半径,在0~200 km。

图4 汽车列车出行距离与出行比例曲线Fig.4 The travel distance and travel proportion curve of car train

表1 曲线拟合结果
注:拟合曲线均1%水平上显著。

图5 累计比例曲线Fig.5 Cumulative proportion curves
累计比例曲线(图5)以累计比例80%为界,不同车型的累计比例曲线呈现出不同的特征。当累计比例小于80%时,从累计速度来看,小客车>中型车>货车>汽车列车;从出行距离来看,汽车列车>货车>中型车>小客车。
1.2.2 距离衰减模式
由于客车与货车的出行对距离的敏感程度不一,可能呈现出不同的距离衰减模式。为探讨客、货车两大特征车型出行规律,将数据重新整合为客车和货车两车型进行分析。
一般的距离衰减函数公式为
Ti=aeβf(di)
(1)
式(1)中:a、β为系数,其中β为距离衰减系数;Ti为距离长度为di的交通流。
目前研究主要基于幂律型与指数型衰减函数展开分析,其他模式的衰减函数参数范围与模型结构的意义尚未得到有效的验证[12]。因此,利用空模型法获取距离效应矩阵,基于路网距离分析距离衰减函数模式中的2种衰减函数形式[3]来模拟河北省域内距离衰减规律(表2),两种模式均通过F检验,客、货车指数型的R-square值均超于指数型,由此判断客、货车的距离衰减函数均以幂律型最适宜。

表2 分车型距离衰减函数模拟结果
1.2.3 客、货车出行特征函数拟合及检验

图6 客车出行距离与出行比例曲线Fig.6 The travel distance and travel proportion curve of passenger car
从图6、图7中可以看出,客车对数正态分布效果最好,曲线拟合结果(表3)中客车拟合优度值指标R-square为0.994 86,SSE为0.001 83,明显高于对数正态分布,期望值为165 km,出行流量主要集中在50~150 km,以中短途出行为主;货车正态分布拟合效果最好,其拟合优度值指标R-square为0.988 36,SSE为0.002 53,明显高于对数正态分布,期望值为214.2 km,大于中国货物运输平均运距181 km[13],出行流量主要集中在100~300 km,以长途出行为主。
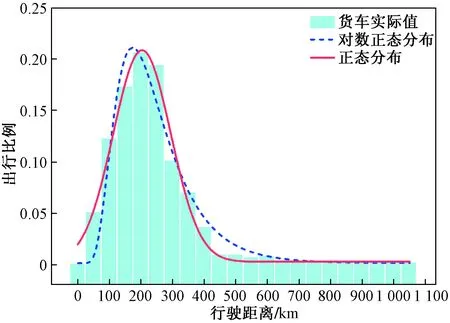
图7 货车出行距离与出行比例曲线Fig.7 The travel distance and travel proportion curve of truck

表3 曲线拟合结果
不同于上述检验方式,为验证客、货车曲线拟合准确性,分别对对数正态分布和正态分布进行Kolmogorov-Smirnova(K-S)拟合优度检验,指定显著性水平取0.05,客、货车两函数结果分别为pk=0.309、ph=0.223,如表4所示,远大于0.05,因此,接受零假设。设客、货车分布函数分别为fk(x)、fh(x),车辆出行里程为t和x,则客车和货车概率分布函数fk(x)、fh(x)可表示为

(2)

(3)
式中:tj和xh分别代表客车和货车的第j个和第h个行驶区间;μ、σ分别表示期望值和标准差。

表4 检验结果
2 基于出行特征的OD估算模型
根据上文中得出的客、货车出行特征,参考高速公路收费站点布置原则,结合交通需求预测时所考虑的相关经济指标,构建OD估算方法。本模型的基本思路是根据各个交通小区(收费站)内驾驶员出行距离与出行比例的总体分布和节点间重要度的吸引程度,将交通小区的交通发生量和吸引量离散到不同出行距离区间上的出行量。
2.1 节点出行概率
设曲线φ(x)为计算节点所在路网内的出行距离与出行比例概率分布函数,则行驶距离区间[bi,bi+1]的交通出行量比例Pi可表示为
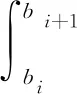
(4)
式(4)中:bi、bi+1为第i个出行区间的行驶距离。
设节点a的交通发生量为Ta,此时区间[bi,bi+1]的出行量即为Ta×Pi。图8所示为高速公路路网示例,圆圈部分为空间上高阳北的交通出行量在行驶距离区间[bi,bi+1]时所覆盖的区域,圆圈区域内所包含的其他节点则成为下一步分配的吸引节点。
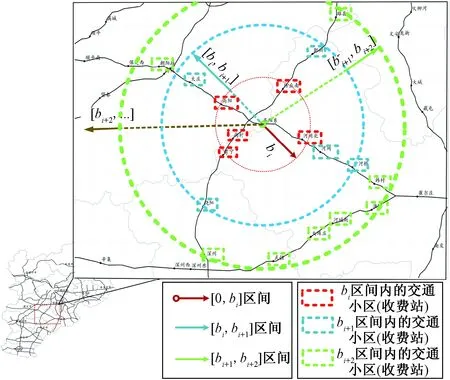
图8 出行距离区间覆盖区域示意图(高阳东站)Fig.8 Schematic map of travel distance interval coverage area(Gaoyangdong toll station)
2.2 节点重要度
为了更客观地反映区域内节点的重要度,通过考虑收费站附近县级的人口、GDP、工业产量、第三产业值和出入口断面流量5个因素来反应该收费站在本区域内的交通重要度,用式(5)表示为
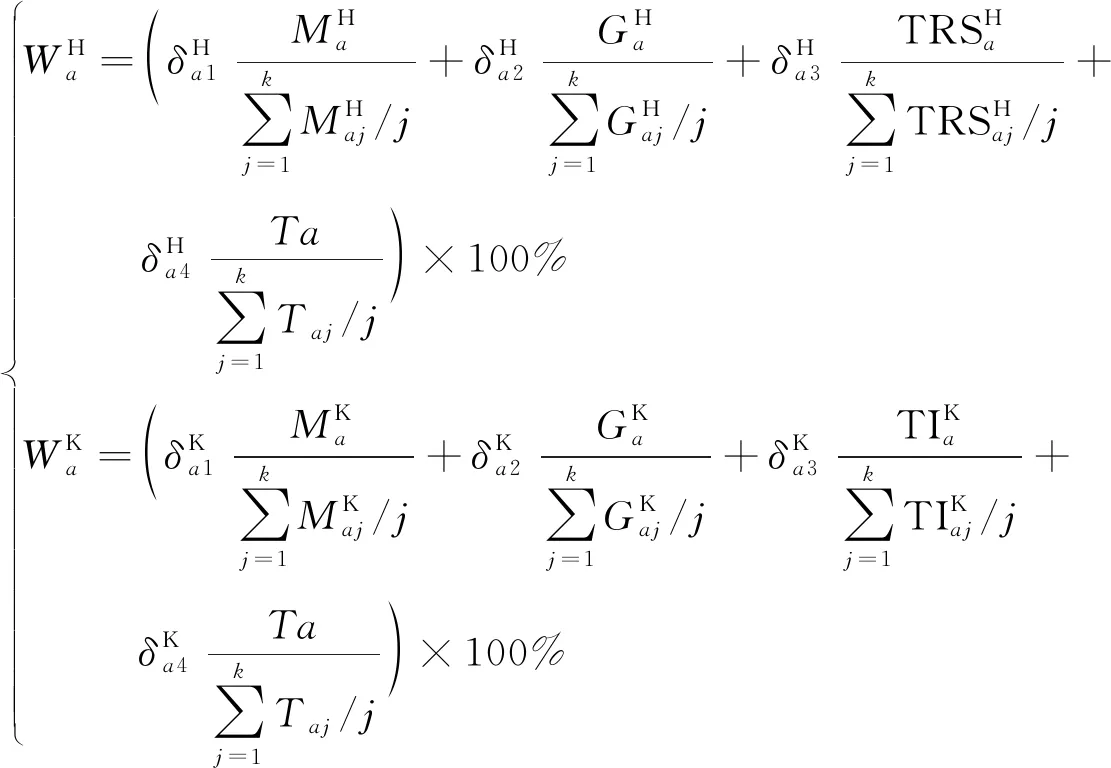
(5)
式(5)中:K、H代表客车与货车;W代表节点重要度;M代表年末人口;G表示地区生产总值,亿元;TRS代表工业产值,亿元;TI代表第三产业值,亿元;δ表示为节点指标的权重;m代表该出行区间内交通小区的个数。
参照重力模型,两个节点之间的重要度吸引量(INA)可表示为

(6)
式(6)中:Lab表示节点之间的距离,km;K代表综合参数;β表示距离衰减系数(1.2.2节所取得的值)。
2.3 OD估算模型建立
与城市路网不同,高速公路路网的交通小区可以以收费站为节点的方式代替,故不存在小区自身的出行距离参数。因此,按上述基本思路,结合式(6)中的各节点重要度吸引力值,求得两节点间的出行量。计算公式可表示为

(7)
计算过程可满足矩阵的发生总交通量的约束:

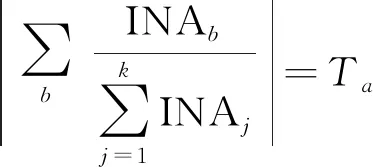
(8)
但不一定满足吸引总交通量的约束,因此,根据节点的吸引总量对矩阵进行再分配。
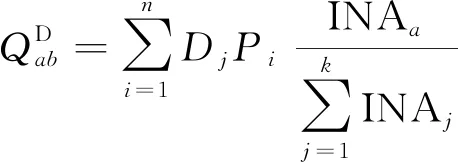
(9)
根据式(7)和式(9)已求得满足发生和吸引约束的OD矩阵,则最终OD矩阵元素可表示为

(10)
如果以求得OD矩阵不能满足精度要求,可利用式(11)进行迭代运算,逐个对元素进行修改。

(11)
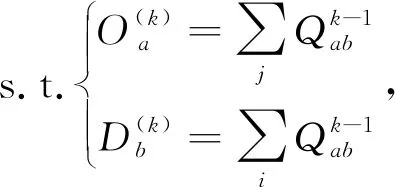
(12)

3 实例验证
以河北省秦皇岛市内京秦、承秦、京哈(沿海)3条高速中各收费站的2018年3月份分车型出入口断面流量数据(表5)和2018年河北省统计年鉴数据为验证数据基础。利用上述计算方法推算OD矩阵。首先,根据已得距离矩阵来确定收费站行车区间个数,同时利用已知客、货车出行概率分布函数确定该行车区间内客、货车交通出行量比例Pi值。其次利用SPSS软件中主成分分析法分别求得节点客、货车重要度中的人口、GPD、工业产量、第三产业量和流量权重值。
然后,根据已得权重值求得每个收费站的重要度,其部分结果如表6所示。
最后,根据式(3)求得节点间的重要度吸引量,进而求得该区间内各节点重要度吸引量比例。进而根据式(4)、式(5)求得OD值,结果如表7所示。利用收费站采集数据对OD估算结果进行检验,估算值与实际值之间的误差均在5%以内,误差值在可接受范围内[10]。

表5 3月份收费站分车型出入口流量

表6 各收费站重要度

表7 秦皇岛市内部分收费站OD估算结果
注:括号内数值为实际量。
4 结论
(1)客、货车出行距离特征曲线分别服从对数正态分布函数和正态分布函数,并且客、货车交通流呈现出不同的出行特征,分别集中在50~150 km与100~300 km区段,较高地契合了公路运输的经济半径与交通流的时空断裂特征;由累计比例曲线可知高速公路交通圈的发展与建设在路网距离上控制在200 km左右最为适宜。
(2)河北省内高速公路客、货车距离衰减函数以指数型函数最为适宜。客、货车距离衰减指数分别为1.934和2.361,说明客车对距离敏感程度更高,适合短距离出行,而货车适合远距离出行,符合实际出行状况。
(3)建立基于车辆出行特征的OD估算模型,充分考虑不同车型驾驶员出行特征和节点间的联系强度,根据实例验证结果数据可知,估算模型具有一定准确性和实用性,有助于对高速公路断面交通量或断面轴载计算等后续工作的开展。

