一种安全校正策略的优化模型

洪 雯，沈 青，鲁爱斌，郑 雪

(武汉电力职业技术学院，湖北 武汉 430072)

第二次工业革命后，电能使用愈发广泛，电力极大促进生产力的快速发展，推动了社会的进步。电力系统在确保安全稳定运行的前提下，最主要任务就是尽可能经济、有效地满足用户的需求，保证持续不间断的供电。而电力系统重要环节之一的输电线路经常跨越山火易发地段，若山火发生在输电线路附近，山火产生的污秽容易引起空气放电，会导致多条输电线路跳闸，此外跳闸线路的潮流将转移到其它线路，可能造成其它线路潮流接连越限，进而发生连锁故障，导致整个系统崩溃，造成长时间的大面积停电事故。

安全校正控制的功能是采取一系列合理措施，在故障初期在短时间内进尽可能解决电网中的各种潮流越限情况，迅速将全网潮流控制在安全范围内，以防止连锁性的事故出现和恶化，将潮流越限的波及范围和经济损失控制在最低程度。因此，山火导致多条线路跳闸后，电网能否安全稳定运行，主要取决于安全校正策略是否正确、合理。

目前，已有的安全校正策略主要是灵敏度法[1-3]和优化规划法[4-5]。灵敏度法通过计算出控制变量对支路潮流变化的关系，然后根据支路潮流的越限量反推出控制变量的调整量来达到消除支路潮流越限的目的，便于操作实施，但是无法处理系统运行中的一些安全约束问题，容易造成原本处于平衡状态的机组出现潮流越限的状况，也可能在调整一些支路的潮流满足约束条件后有其他的支路出现了潮流越限的情况。优化规划法通过求解数学模型得出控制方案，因为可以设置复杂的约束条件和合理的目标函数，故而有较好的安全性和经济性。

针对山火故障导致的多条输电线路跳闸进而出现的潮流越限问题，本文采用优化规划类算法，根据当前系统状态进行在线安全校正，以期在短时间内恢复系统正常运行，避免连锁故障的发生。

1 安全校正策略的优化变量

本文选择优化规划类方法制定安全校正策略。安全校正策略的优化模型对电力系统进行了合理的简化，将发电机和负荷的参数调整问题转化为建立、求解非线性的连续和二元混合规划问题。首先基于启发式搜索原理确定优化变量，然后以负荷总有功切除量最小为目标函数，将系统运行中的常规和频率约束作为约束条件，建立优化模型，并基于改进二元粒子群算法对该模型进行优化计算，求解得出满足约束条件且目标函数最小的安全校正方案。

当某电网出现支路潮流越限时，则需要进行发电机有功和无功功率调整和切负荷等操作来消除越限。对于实际电网，节点数众多，若想逐一调整所有的发电机和负荷显然是一件既费时又费力的事情。针对这种情况，本文采用启发式搜索来确定优化变量。

所谓启发式搜索指的是在状态空间中对系统中所有可能的优化变量进行评估，得到优化变量中最好的一部分，这部分最好的变量即为下一轮的搜索范围，直到找到目标，通过这样的方法，能避开大多数没有意义的搜索过程，节约搜索时间，提高搜索速度。

本文基于负荷转移因子，筛选出对潮流越限的支路、效果最好的发电机和负荷节点，将这些节点作为优化变量，大大缩减了优化变量的数量，缩短了优化时间。

1.1 负荷转移因子

负荷转移系数是指发电机和负荷节点的网络注入功率的变化引起支路潮流变化的比例系数。该系数越大，在该节点进行单位出力的调节，过载支路上潮流变化趋势越大，这样就能保证在调节量尽可能小的情况下达到所需的效果。

定义负荷转移因子为母线注入电流变化时，电网中每一条线路上电流的变化，即：

(1)

式中：ΔIk表示母线注入电流的变化量；ΔIij表示母线k电流的变化在线路ij上所引起的电流变化量。

根据基尔霍夫定理1的推导，可得网络方程可表示为U=ZI，其中，Z为阻抗矩阵，进一步得到母线电压变化量与母线注入电流的关系：

(2)

进一步得到负荷转移因子：

(3)

负荷转移因子表示的是节点k负荷出现功率变化时, 在支路ij上所导致的功率变化。其中，Zik、Zjk为阻抗矩阵的元素；zij为线路ij的阻抗。

计算出每一个节点分别对每一条越限支路的负荷转移因子后，从中筛选出对每一条越限支路影响较大的节点的集合，这些发电机节点即为对该条越限支路调节效果最好的一类发电机。

1.2 连续型变量

采用启发式搜索的方法，基于负荷转移系数得到对潮流越限支路潮流调节效果最大的部分发电机。由于发电机的有功功率是通过调整原动机出力、无功功率是通过调整励磁参数实现的，故可以实现连续调节。

由于切除负荷只能有功和无功同时切除，如果切负荷后，不相应调整发电机的有功和无功功率，系统有功和无功就无法同时满足平衡，可能出现频率或者电压失去稳定的问题，因此将发电机的有功和无功均作为连续型优化变量。

确定连续型变量的步骤如下：

1)首先基于1.1节的方法计算出所有发电机对待调节支路A的负荷转移因子(Load Shift Factor, LSF)并从大到小排序；

2)然后筛选出对该待调节支路潮流调节效果最好的发电机节点xA；

3)重复步骤1)和步骤2)，依次得到对第i个待调节支路潮流调节效果最好的发电机节点xi；

4)对这些发电机节点取并集即得到对所有待调节支路调节效果最优的发电机节点的集合，将这些发电机节点的有功、无功功率作为连续型变量x。

1.3 0-1二元变量

由于负荷无法实现连续调节，只能切或者不切，所以在切负荷控制中，对于负荷的控制是一个0-1优化的问题。并且不一定每个负荷节点都只有一个负荷，对于有多个负荷的负荷节点，每一个负荷都是独立的，应当分别考虑，而不是全部切除或保留。

确定0-1二元型变量的步骤如下：

1)首先基于1.1节的方法计算出所有负荷对待调节支路A的负荷转移因子(Load Shift Factor, LSF)并从大到小排序；

2)然后筛选出对该待调节支路潮流调节效果最好的负荷节点yA；

3)重复步骤1)和步骤2)，依次得到对第i个待调节支路潮流调节效果最好的负荷节点yi；

4)对这些负荷节点取并集即得到对所有待调节支路调节效果最优的负荷节点的集合yk；

5)由于文中负荷节点在实际中指变电站，而负荷指变电站的每条出线，因为变电站出线上的功率无法实现连续调节，故将变电站集合yk中每条出线的切除与否作为独立的0-1二元型优化变量y，1表示保留该条出线，0表示断开该条出线。

1.4 优化变量的初值

优化变量初值的选取对整个优化结果有较大的影响，一个好的初始值能让优化过程更为快捷，取得更好的优化效果。

在优化中，通常是随机生成的一组数据，将该数据赋给变量作为初始值。但是在电力系统中，采用这种方法随机性太强，如果某一次优化的初始值不好，甚至无法得出可行解。故而在本文中，以系统故障前优化变量的值作为初始值。经过多次试验证明，这样不仅更快捷，并且得到的最终结果优化变量的改变量也更小。

2 安全校正策略的目标函数

为了尽可能满足对用户的供电，保持供电的连续性，故而希望安全校正得出的方案中负荷有功总切除量最小。设置目标函数为：

式中：n为二元型变量个数；PLi为二元型变量i的有功功率；yi为二元型变量i的值，0表示该负荷被切除。

3 安全校正策略的约束条件

为了保证安全校正的安全性，故设置以下约束条件：

1)节点电压约束：Vmin≤V1,2…n≤Vmax

2)发电机有功上下限约束：Pgmin≤Pg1,2…m≤Pgmax

3)发电机无功上下限约束：Qgmin≤Qg1,2…m≤Qgmax

4)负荷有功上下限约束：PLDmin≤PLD1,2…n≤PLDmax

5)支路潮流约束：PLine≤PLinemax

6)发电机视在功率约束：Sgmin≤Sg1,2…m≤Sgmax

7)功率因数约束即发电机的功率因数应该保持使发电机正常工作的一定范围之内，不得低于设定值：η1,2…m≥ηmin。

在本文中，以上约束的实现方法是通过在目标函数中加入惩罚函数部分。其原理是，通过在惩罚函数前加一个非常大的系数，该系数通常为目标函数的数量级倍数，可使惩罚函数的数量级远远大于目标函数本身的值。一旦发生越限，目标函数就会变的相当大，而安全校正方案的目标函数是负荷有功总切除量最小，这一组解自然就会被排除。

4 优化模型的求解方法

在实际电力系统中，负荷是不可能实现连续调节的，所以模型采用改进二元粒子群优化算法(Improved Binary Particle Swarm Optimizer, IBPSO)求解二元变量最优规划问题。

IBPSO基于两个假设：

1)对于0-1二元变量y，由于优化过程中y的极值点yopt未知，假定yopt取0或1的先验概率均为0.5；

2)在寻找的过程中，个体极值Pbest和全局极值Gbest对最佳值的判定是独立的。

记Pbest作出正确判断的概率为pp，Gbest作出正确判断的概率为pg，由于Pbest和Gbest是粒子群迭代过程的历史最优值，它们分别发现全局最优解yopt的概率超过平均值，因此pp>0.5，pg>0.5。并且，为促使粒子群分散搜索，避免陷入局部最优，要求pp>pg。取pg=0.8，pp=0.7。应用概率论中的条件概率Bayes公式，引入参数α和β，记：

(5)

通过式(5)计算得α=0.9，β=0.7，迭代次数为q+1时，二元粒子位置向量yq+1的0-1决策的依据如下。取r=rand，有：

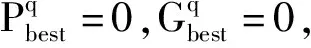
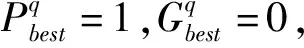
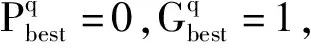
模型基于二元粒子群优化算法，通过调用电力系统分析综合程序(Power System Analysis Software Package，简称PSASP)进行潮流计算来进行安全校正优化模型的求解。安全校正优化模型的整体求解流程图如图1所示。

图1 安全校正优化模型的整体求解流程图

5 算理验证

5.1 故障设置

采用华中某省电网的潮流数据进行算例验证，对该电网应用上节的结构脆弱性计算方法，综合2018年的该电网交流线路、母线、两绕组变压器和三绕组变压器参数，和该电网网架数据，得到该电网网线路脆弱性排序结果。在得到的排序结果中筛选出500 kV等级的交流线路，根据数值大小进行排序，并节选了排序靠前的部分结果列入表1中。数值越接近1，表明该条线路退出对该电网网的结构稳定影响越大；数值越接近0，则该条线路退出运行对该电网网结构稳定性影响越小。

表1 某电网500 kV交流线路脆弱性排序表(节选)

山火虽有突发性，但均发生在植被茂密地区和干燥、高温天气。在上表中从上往下观察，由于艳山红500母线所处的地理位置在山区附近，所以本研究假设序号为2和3的两条线路因山火跳闸。本研究假想的山火导致输电线路跳闸的故障形式如表2所示。

5.2 优化变量

由于不同的故障类型，需要优化的优化变量不同。所以针对本研究的假想故障，本节基于上节所述方法，选取该故障形式下对应的优化变量。

5.2.1 待调节支路的选取

断开上述两条线路后，重新计算全网潮流。对于所有的约束条件，此时只有支路潮流越限，节点电压未发生越限。其中发现，故障线路跳闸后，有4条线路的功率显著增加，故选取这4条线路为待调节支路，即应该选取对这4条线路潮流影响较大的发电机和负荷作为优化变量。这4条线路如表3所示。

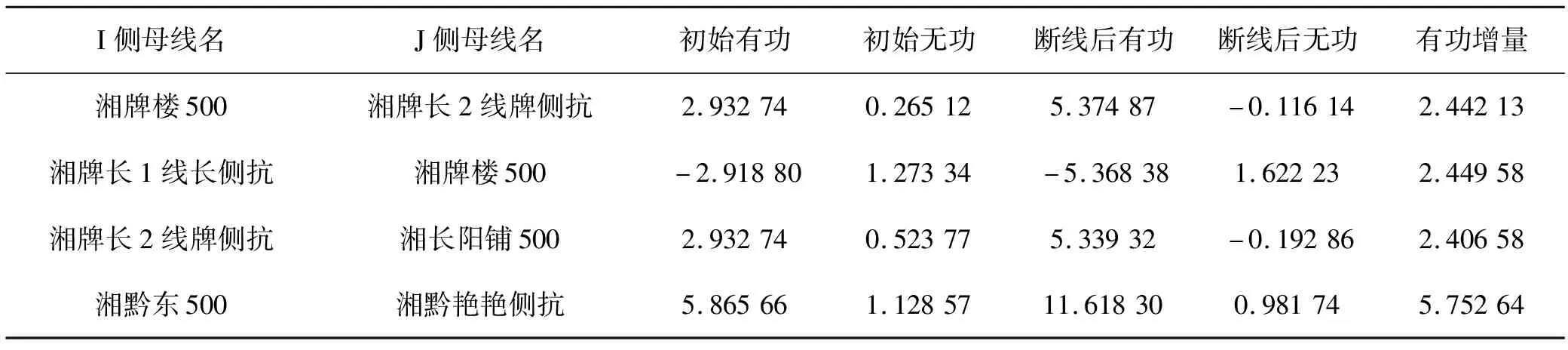
表3 待调节支路表达式表 p.u.

5.2.2 优化变量的选取

根据第1节所述方法得到优化变量如表4所示，其中负荷转移因子越接近1，表示影响程度越大。

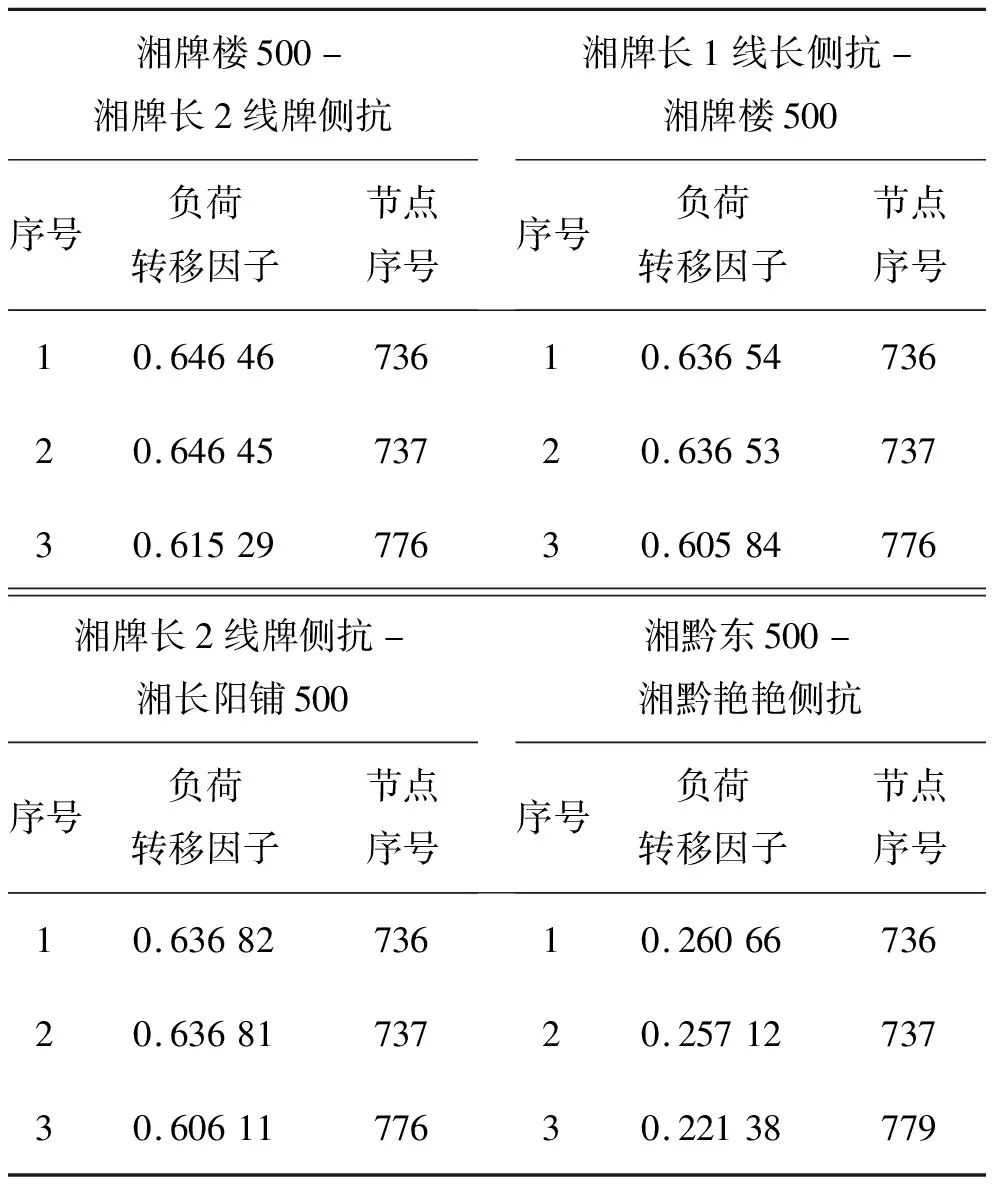
表4 优化变量表(节选)

5.2.3 优化变量的初值

连续型优化变量的初值(以及上下限)如表5所示。0-1二元型优化变量的初值如表6所示。值得注意的是，文中负荷节点在实际中指变电站，而负荷指变电站的每条出线。假设每个变电站有4条出线，则相当于负荷节点的功率只能以1/4为为最小切除单位进行切除。

将以上发电机和负荷节点的的有功和无功功率作为优化对象进行优化。

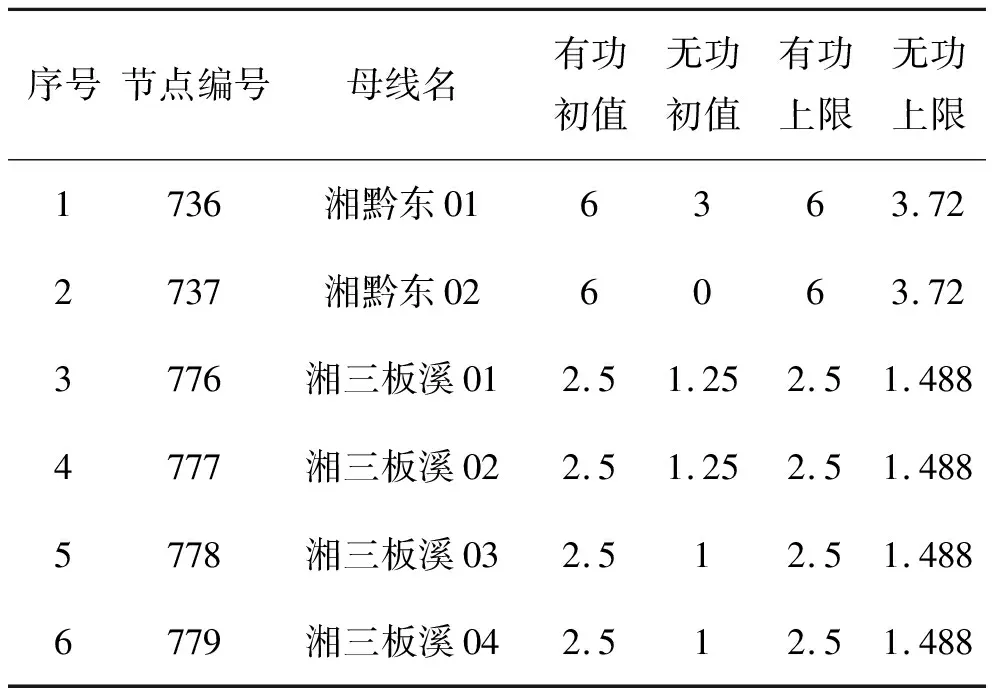
表5 连续型优化变量的初值表 p.u.

表6 0-1二元型优化变量的初值表 p.u.

5.3 安全校正方案

基于优化模型和求解方法，得出安全校正方案。表7列出了发电机的安全校正方案，表8列出了负荷的安全校正方案。

5.4 安全校正方案校核

根据优化出的安全校正方案修改相应的发电机和负荷功率，重新计算全网潮流，得到安全校正方案对故障后越限值较大的4条线路的调整效果，也就是待调节支路优化前后的有功值变化情况，如表9所示。

从表9中可以看出，按照优化得到的安全校正方案调整后，该电网的潮流均降至安全稳定范围内，不再有发生连锁故障的隐患，安全校正方案的有效性得到验证。

表7 发电机安全校正方案表 p.u.

表8 负荷安全校正方案表 p.u.

表9 待调节支路的优化效果表

5.5 结果分析

通过对比表5和表7中优化变量的优化结果和原始数据，发现优化后发电机的功率都有所减少，三个负荷节点中，湘黔东01的负荷全部切除，湘黔东02的负荷全部保留了。之所以优化出的结果是切机和切负荷，是因为这些节点对待调节支路的调节效果均为正相关，即减小这些节点的功率，可以使得待调节支路的潮流相应减少。反之，若某些节点对待调节支路的调节效果为负相关，则可能需要通过增发功率才可以相应减小待调节支路的潮流。

通过对比安全校正方案调整前后的潮流结果，发现优化后，系统的潮流相比故障后都显著减少。对比优化后该电网潮流和原始潮流，发现优化后的潮流较为贴合原始潮流数据，只是略有小幅增加，但也没有超过潮流极限值，由此验证了优化模型求得的安全校正方案的合理性和正确性。

6 结 语

本文详细介绍了一种安全校正策略的优化模型，该模型将复杂的发电机和负荷的参数调整问题转化为建立、求解非线性的连续和二元混合规划问题，通过限定粒子群算法中粒子的搜索域来实现对优化变量的参数调节范围的约束，并通过求解数学模型得出控制方案。从根本上避免了越限和一些不符合实际的结果，也去除了大量无效的搜索范围，使得在更短的时间可以得到合理有效的安全校正方案。