弹性轨道磁悬浮控制系统模型降阶研究*
刘武斌,王 泉
(1. 中铁磁浮交通投资建设有限公司, 湖北 武汉 430060; 2. 湖南凌翔磁浮科技有限责任公司, 湖南 长沙 410600)
磁悬浮系统由于其固有的优势,得到了越来越广泛的应用,比如磁悬浮列车、磁悬浮轴承、磁悬挂天平等。特别是随着磁悬浮列车技术的飞速发展,引起了广泛的关注。磁悬浮列车已经进入应用阶段,但是磁悬浮系统本身还在逐步地完善,特别是车轨耦合振动问题还没有得到完美的解决。当列车行驶在钢梁上时,可能出现车轨耦合振动。磁悬浮系统是一个非线性不稳定系统,需要主动控制才能确保系统的稳定性。常见的磁悬浮控制方法有极点配置法[1]、PID控制方法[2]、非线性控制方法[3],鲁棒控制法[4],自适应控制法[5],变结构控制方法[6]等。采用上述控制方法时,通常假设轨道是刚性的。这种假设在某些磁悬浮系统上是可以成立,而且对系统稳定性的影响不明显。然而,实验表明:对于磁悬浮列车系统来说,当列车行驶在钢梁上的时候,如果采用基于刚性轨道系统模型设计出来的控制算法进行试验,可能发生车轨耦合振动,严重时会使得系统发散。针对轨道弹性给控制系统带来的影响,磁浮研究工作者进行了大量的研究工作,武建军等[7-9]分析了磁悬浮列车的动力学特性及系统的稳定性,为考虑轨道弹性的控制算法设计提供了依据;Lagos等[10]分析了车辆过道岔时,轨道弹性对系统的影响;李晓龙等[11]等提出一种新型的抑制车轨耦合振动的方法;另外,还有其他磁浮研究人员针对轨道弹性对系统的影响开展了研究[12-15],得出了一些抑制车轨耦合振动的方法。为了分析轨道弹性对系统的影响,本文在刚性轨和弹性轨道条件下,分别建立了磁悬浮系统的数学模型;分析了基于刚性轨道设计出的控制系统在弹性轨道上不能使得列车稳定悬浮的原因;利用Hankel 范数近似法,对弹性轨道条件下建立的悬浮系统模型进行合理降阶;对降阶后的系统设计了控制器,确保列车的稳定性。
Hankel范数近似法是一种有效的模型降阶方法[16-17],它是从Hankel奇异值角度给出原系统的一种平衡、渐近稳定的降阶实现,同时还给出对模型降阶误差的一种估计。这种方法首先计算出系统的Hankel奇异值,然后对比系统的奇异值,将其中明显比其他奇异值小的去掉,去掉一个奇异值就相当于对系统进行降一次阶次,去掉两个奇异值相当于降阶两次,以此类推。
1 Hankel范数逼近

当系统为稳定有理系统时,可以直接利用定理1对系统进行模型降阶;当系统为不稳定系统时,若要利用上述定理对系统进行模型降阶,有两种思路:
1)将系统进行线性变换,分解为稳定部分和不稳定部分。针对稳定部分,再采用上述定理进行降阶处理。
2)求出系统的Hankel范数,根据截断误差决定要舍弃哪些状态,然后再判断舍弃的状态是否为系统的稳态部分,若舍弃的为稳态部分,则可以直接求出原系统的降阶模型。
本文在研究分析磁悬浮系统时,采用了思路2的方法。
2 建模
在传统电磁铁中加入永磁,即为混合磁铁。混合磁铁利用永磁提供大部分的悬浮力,能降低悬浮功耗,减少电磁铁的发热,是磁悬浮技术的重要发展方向。混合磁铁的结构见图1。其中,δ为悬浮间隙,F为磁铁与轨道之间的悬浮力,u为线圈两端的电压,i为线圈电流,δm为永久磁铁的厚度,A为永磁磁极面积,与电磁铁的磁极面积相等。设永久磁铁的相对磁导率为μm,矫顽力为Hc,磁铁线圈匝数为N。
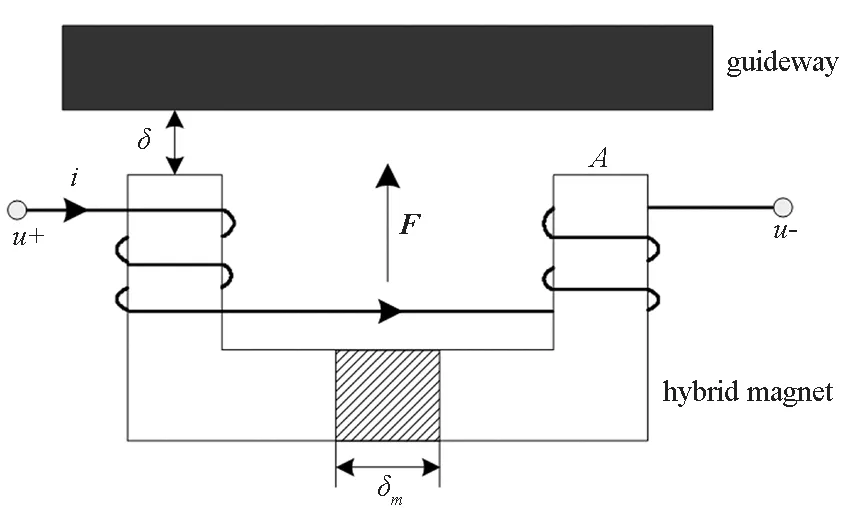
图1 混合磁铁结构示意图Fig.1 Structure of a hybrid magnet
2.1 基于刚性轨道的系统建模
为简化模型,忽略磁路漏磁,忽略电磁铁和导轨的磁阻,忽略轨道的弹性,则图1所示的系统模型[18]如下:
(1)
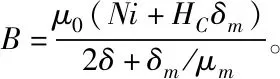
把方程组(1)在平衡点(i0,δ0)处线性展开,并选取系统输入为控制电压的变化量Δu,输出y=Δδ,得到在刚性轨道条件下系统的传递函数为:
(2)
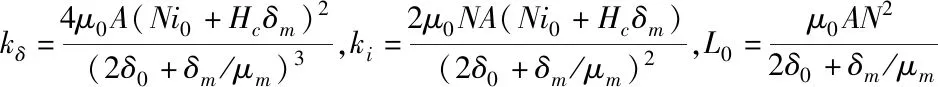

表1 P0(s)的劳斯表Tab.1 Routh table of P0(s)
从表1可以发现其劳斯表的第二列数据发生了符号变化,说明系统存在实部为正数的根,从而可知系统不稳定,需进行控制。
2.2 基于弹性轨道的系统建模
简单又不失一般性,假设轨道梁是简支梁,且只有一阶振动模态,轨道梁的振动方程[3]为:
(3)
其中:yG是轨道相对于惯性基的垂向位移;a由轨道结构决定,代表轨道弹性的强度;ω1和ξ1是轨道一阶振动的频率和阻尼;y为电磁铁在垂直方向上相对于惯性基的位移。考虑轨道弹性后,系统的电磁力方程和电学方程仍然成立。只有动力学方程产生变化[15]:
(4)
结合式(1)和式(4),将模型在平衡点线性展开,得到弹性轨道下的混合磁铁模型为:
(5)

3 刚性轨道下的模型分析
为了分析模型之间的差异,以模型之间的范数差作为指标,模型之间的范数相差越大,表明两个模型之间的差别越大。
某混合磁悬浮系统的有关参数如下:m=500 kg,A=1×10-3m2,δ0=0.01 m,N=300匝,R=0.5 Ω,μm=1,δm=0.02 m,Hc=800 kA/m,轨道一阶模态参数ω1=17×2π ,ξ1=0.005,a=0.025。将上述参数代入式(2)和式(5),得到刚性轨道系统模型和弹性轨道系统模型:
(6)
(7)
其中:
N(s)=s5+177.9s4+1.16×104s3+1.411×106s2-
1.851×105s-1.977×109
由此得出刚性轨道系统模型的无穷范数:
弹性轨道系统模型的无穷范数:
二者之间的模型相对误差:
可见,以刚性轨道系统模型为准,模型误差的最大值可达原系统的1.85倍,该值在频率15~16 Hz处取得,该频率接近某类轨道频率,比如钢梁,可能引起车轨耦合振动。因此,在设计悬浮控制器时,不能简单地忽略轨道弹性。
4 弹性轨道下的模型降阶
考虑轨道弹性后,系统模型增加为5阶,系统变得更加复杂,不便于系统分析,同时也给控制器的设计和实现带来困难。为此,考虑对弹性轨道系统模型进行降阶。
由定理1可知,基于Hankel范数逼近的方法适用于有理、稳定的系统。由式(5)所描述的模型看出,本系统为有理系统。由系统的稳定性判据可知,本系统是不稳定的,因此不能直接采用定理1进行降阶处理。这里采用定理1所描述的思路2对本系统进行分析处理。

表2 模型降阶的相对误差Tab.2 Relative error of model reduction
从表2可以看出,降阶模型在3阶以下带来的误差较大,而将模型降为4阶带来的误差约为3%,故模型可以考虑降为4阶。
根据控制理论相关知识可以判断出,σ5对应的系统状态为稳定状态,因此舍弃该状态不会影响系统的稳定性。由定理1,可以将系统降为4阶。模型降为4阶后,传递函数为:
(8)
式(6)基于刚性轨道建立的系统模型P0、式(7)基于弹性轨道建立的系统模型P1,及式(8)基于弹性轨道建立的系统4阶降阶模型。三者的波特图见图2。比较P0和P1可见,二者系统幅频特性和相频特性差别很大,尤其是在低频段,P1有180°的相位滞后,这极有可能导致控制器失效,由此说明基于刚性轨道系统模型设计的控制器不能使系统有效悬浮;比较Pr和P1可见,降阶后的模型Pr保留了P1在关键频率段的幅频特性和相频特性,只是在高频段有较大差别。但是,高频段超出悬浮系统的频率范围,在该频率段的幅频差异并不影响系统特性,可见系统的4阶降阶模型是有效的。
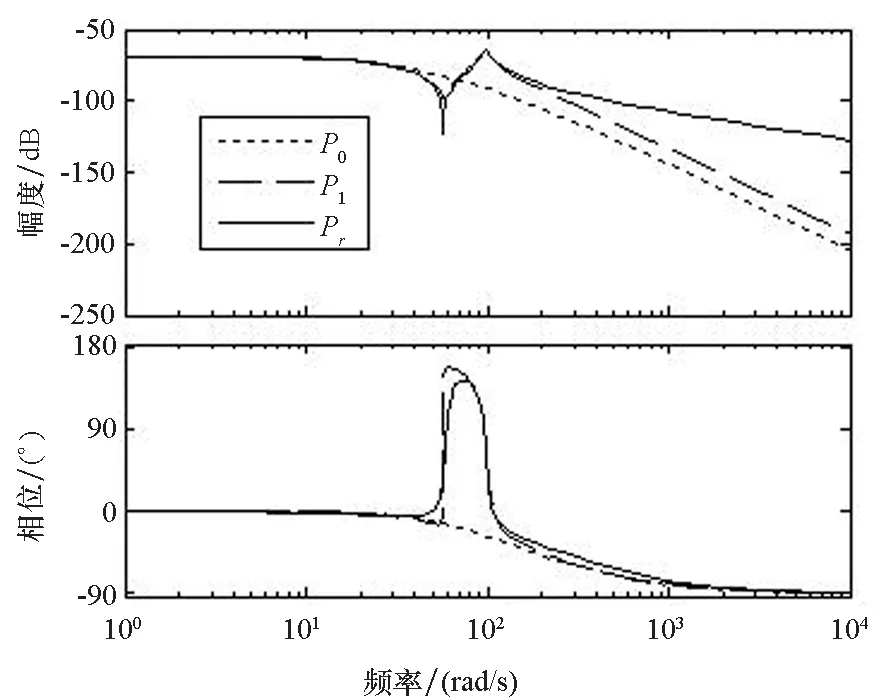
图2 P0、P1、Pr的系统波特图比较Fig.2 Comparison of system Bode diagram for P0、P1、Pr
5 仿真验证
仿真时,采用常见的状态反馈控制,这里分别针对刚性轨道下的系统模型P0和弹性轨道下的系统降阶模型Pr设计反馈控制器。对于P0,设计的控制器的传递函数H0(s)=-9772-291s;对于Pr设计的控制器的传递函数H1(s)=-3600-60s。令初始悬浮间隙是20 mm,稳定悬浮间隙是10 mm,得到H0和H1作用下的间隙响应见图3。
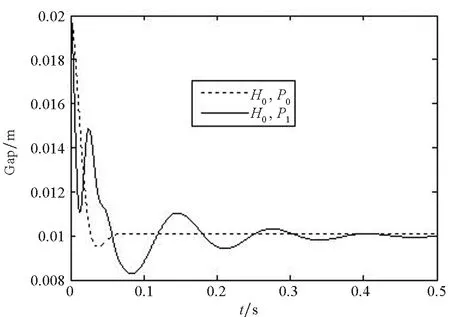
(a) H0控制下的间隙响应(a) Gap response controlled by H0
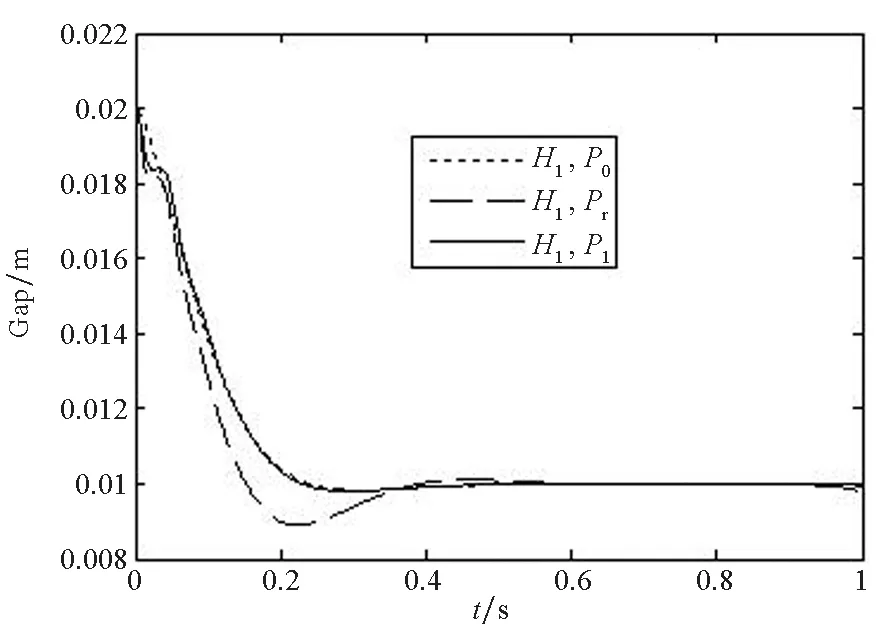
(b) H1控制下的间隙响应(b) Gap response controlled by H1图3 起浮过程中的间隙Fig.3 Air gap during the levitation process
其中,图3(a)是H0控制P0和P1的波形,可以看出H0用于控制P0,得到很好的悬浮效果;而H0用于控制P1时,系统性能变差。图3(b)是H1用于控制P0、P1和Pr时的间隙变化波形,从图中可以看出,基于降阶模型设计的控制器,既能使得刚性轨道系统模型稳定,也能使得弹性轨道系统模型稳定,且悬浮性能较为一致。
6 结论
为分析轨道弹性对系统性能的影响。本文建立了刚性轨道系统模型和弹性轨道系统模型,并根据二者的范数差,指出在某些情况下,不能忽略轨道弹性的原因。刚性轨道系统模型下的控制算法不能确保弹性轨道的稳定性,而弹性轨道系统模型下的控制算法复杂而难以实现。为解决上述问题,本文提出了对弹性轨道系统模型进行降阶的方法。采用Hankel 范数近似法对系统模型进行降阶处理,利用模型之间的范数差选择合理的系统阶次,确保降阶模型在关键频段的频谱特性与原模型一致。最后,分别针对刚性轨道系统模型和降阶模型设计控制器,仿真结果表明:刚性轨道系统模型下设计的控制器不能确保弹性轨道系统模型的良好性能,而基于降阶模型设计的控制器能确保弹性轨道系统模型的稳定悬浮。由此验证了模型降阶的有效性。

