二维可压缩流动抽吸流量模型及验证*

张宝虎，赵玉新，柳 军

(国防科技大学 空天科学学院， 湖南 长沙 410073)

进气道是高超声速飞行器的重要组成部分，由唇口处反射激波产生激波边界层干扰现象，形成一定大小的分离区，在一定的情况下造成进气道不启动，而抽吸是解决高超声速进气道不启动的有效手段[1]，能够以较小流量损失有效提升进气道起动性能。边界层抽吸的物理实质是抽吸掉部分低速流体，增加高速流体在边界层中的比例。抽吸质量流率是抽吸装置设计最为关键的因素，特别是在高超声速进气道的隔离段，抽吸对于尾部正激波的稳定控制具有重要的作用[2-4]。这是因为激波前后满足质量守恒关系，正是通过抽吸流率控制尾部激波的位置，为燃烧室提供均匀稳定的气流。边界层抽吸带走了一部分质量，会对燃烧室产生一定的影响，因此对这部分抽吸质量的准确有效预估需要一个有效的抽吸模型[5]。

Harloff等[6]总结了超声速平板抽吸的各种经验性模型，这些经验性模型很多都是通过经验关系确定抽吸孔处的流速来确定抽吸流率模型。Doerffer等[7]通过抽吸孔处的压差确定有效马赫数，然后按照一维等熵流动的形式建立质量抽吸流率模型。Bunnag[8]通过观察圆孔抽吸的数值模拟结果，根据对称面的流场特征，基于膨胀波与激波理论，建立了圆孔的抽吸流量模型。 Kim[9]认识到了Bunnag模型的不足之处，通过在流量系数中耦合壁面条件，进一步提高了模型的精度。这些模型都是在具有边界层、黏性干扰、激波、膨胀波等复杂流场结构下建立的，很难发现主导抽吸的核心因素以及相互之间的耦合因素，对于抽吸流动本质问题的把握不是很清晰。

圆形抽吸孔具有结构对称性，在高超声速飞行器具一定侧滑角的情况下可以保持流场结构不至于有大的突变，成为抽吸装置的首选结构。在一定的超声速来流条件下，圆孔前缘对于来流具有不同的后掠角，根据来流在垂直于圆孔边缘方向的速度分为超声速前缘和亚声速前缘。根据抽吸孔的尺度与边界层厚度的关系，超声速边界层抽吸流场结构可以分为三种情况：当边界层厚度远大于抽吸孔的尺度时，对应亚声速抽吸；当边界层厚度与抽吸孔的尺度相当时，这是一种临界情况，具有非线性效用；当边界层厚度远小于抽吸孔尺度时，以超声速抽吸为主导，边界层对抽吸流率的影响可以转化为位移厚度对抽吸孔尺度的影响，进而等效为超声速抽吸。因此无黏亚声速与超声速抽吸是抽吸研究的基础。

本文从流动的角度，简化复杂的抽吸控制装置[10-12]，针对无黏均匀来流，首先给出超声速抽吸模型，导出壅塞发生条件，然后给出亚声速抽吸模型以及壅塞条件和数值拟合结果。

1 超声速抽吸模型

在来流静压、静温和马赫数给定的情况下，超声速抽吸可以分为两个阶段：一个阶段是随着压比的降低抽吸流量系数逐渐增大，另一个阶段是当压比降低到一定的程度的时候，抽吸流量系数不再随压比的降低而降低，这种现象称为壅塞。抽吸模型应该准确反应这两个阶段。超声速流动的扰动只能向流场下游传播，而不能向上游传播，这是超声速流动的最基本特征。在抽吸孔的小尺度范围内确定流动结构的依据是Prandtl-Meyer膨胀波理论。

1.1 超声速非壅塞抽吸模型

在实验与数值模拟中都可以认识到抽吸是一种压差驱动的物理现象[7，13-14]，抽吸孔处的压力通过膨胀波使得主流区域的流线偏转并加速。建立超声速抽吸模型的基本假设是:

1) 抽吸孔前缘是超声速流场的扰动点，抽吸孔处产生膨胀波，扰动沿膨胀波方向传播，膨胀波后的流线是直线，因此在垂直于流线方向没有压差，压强等于抽吸孔后的背压。

2) 抽吸质量流率主要取决于背压，背压通过改变抽吸孔处的气流偏转角度进而改变抽吸质量流率。

3)抽吸孔的深度t和孔径L相比非常小,平板视为无厚度，即t=0。

已知来流条件马赫数M∞、压力p∞和温度T∞，同时已知抽吸孔处的背压pb,γ为气体比热比，由等熵流动关系[15]确定抽吸孔处的物理量马赫数Mb、温度Tb和密度ρb。

(1)

(2)

(3)

图1为二维抽吸孔流动结构。由图1可知，膨胀波后流线为直线，对于一定的抽吸孔尺度L，对应于最后一道膨胀波有一个尺度Leff，这个尺度内的气体全部进入抽吸孔。假设最后一道膨胀波与波后流线的马赫角为μ2，R为气体常数，则抽吸质量流率为

(4)

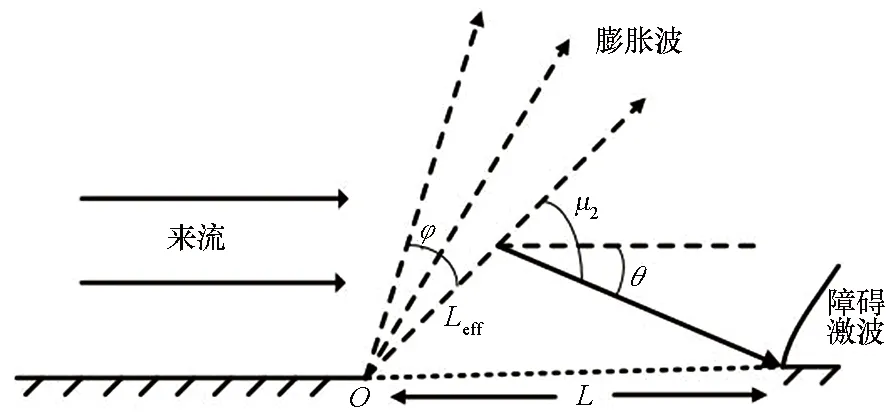
图1 二维抽吸孔流动结构Fig.1 Flow structure of 2D bleeding hole

图1中物理量满足如下关系式

(5)

所以由式(4)～(5)有

(6)

其中，θ为流线偏转角度，由Prandtl-Meyer[16]关系得出

θ=υ(Mb)-υ(M∞)

(7)

由来流条件与背压通过式(6)可以求出抽吸孔处的质量流率。

定义流量系数为

(8)

(9)

式中pt和Tt分别为来流总压和总温度，则超声速抽吸流量系数为

(10)

其中，Mb和θ分别由式(1)和式(7)确定。

通过Fluent数值模拟结果和模型的对比来验证模型的有效性。选择来流马赫数M∞=2.0，通过改变背压获得不同的流量系数,图2为模型与数值模拟结果的对比。

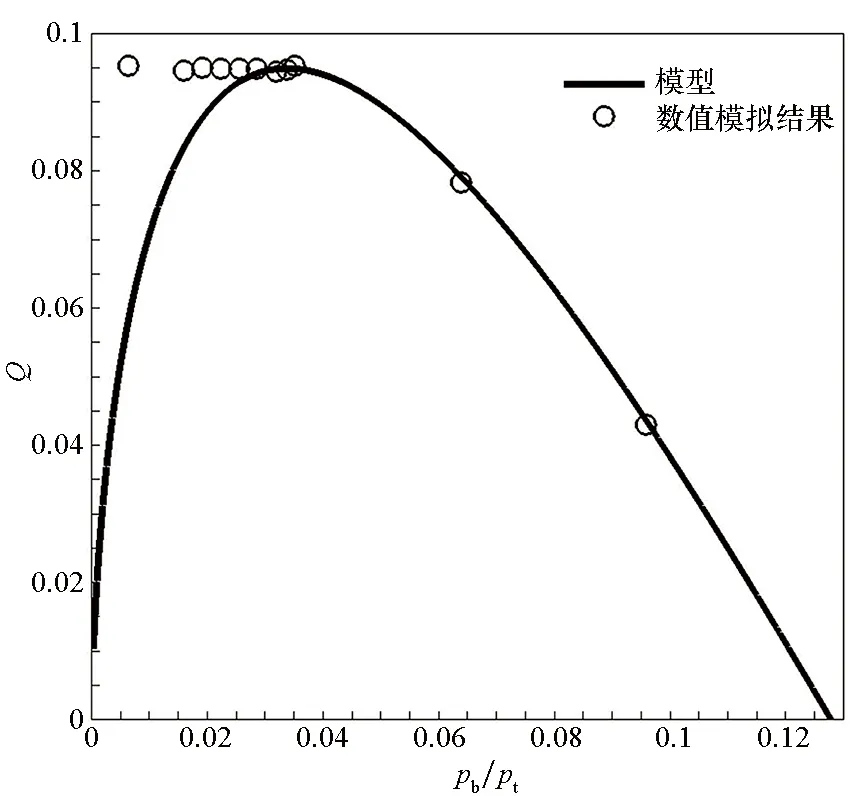
图2 超声速抽吸模型验证Fig.2 Validation of supersonic bleed model

通过图2可以看出，在高压比的情况下，理论模型和Fluent数值模拟结果基本一致，但是在低压比的情况下，模型流量系数随着压比的降低而降低，没有出现壅塞现象，而数值模拟结果出现了壅塞现象。

1.2 超声速抽吸壅塞模型

壅塞是超声速扰动不能向上游传播的结果，确定壅塞发生的条件很关键[17]。因为在很多情况下，高超声速进气道中的压力很高，高超声速飞行器飞行工况下的外界压力很低，抽吸装置往往是在这种条件下工作。

通过超声速抽吸模型可以很容易地确定壅塞发生的条件。在来流条件一定的情况下，背压是确定抽吸质量流率的关键因素。在背压减小到一定程度时，质量流率有一个极值点，对应抽吸质量流率的导数为零。用背压对式(6)，也即对抽吸质量流率求导，令其为零，有

(11)

可获得壅塞发生的条件为

Mbsinθ=1

(12)

即

(13)

其中，θ由式(7)确定。

式(13)是由超声速抽吸模型获得的壅塞条件，表明在垂直于抽吸孔入口方向上的马赫数M⊥=1的时候壅塞发生，如图3所示。类似于超声速喷管的喉部壅塞，但是和喷管由亚声速加速到超声速的流动有根本的不同，因为膨胀波后的流动是超声速的。由式(12)和图2可以看出，抽吸壅塞条件仅仅与来流马赫数和压比有关系，和温度没有关系，对应于抽吸模型的极值点。

图3 壅塞机理示意图 Fig.3 Illustration of choking mechanism

1.3 超声速抽吸模型验证

基于以上超声速抽吸模型及其壅塞条件，令

(14)

(15)

则超声速抽吸流量系数为

(16)

Mbsin[ν(Mb)-ν(M∞)]=1

(17)

通过Fluent数值模拟来验证上述流量系数，数值模拟选择来流马赫数M∞=2.0，改变背压，计算结果如图4所示。通过流量系数可以看出，在很宽的压比范围内，抽吸模型与壅塞模型和数值模拟结果基本一致，说明以压力作为建立模型的切入点是正确的，体现了抽吸是一种压力驱动的流动现象，证明抽吸模型的假设是有效的。

图4 壅塞与非壅塞条件下的流量系数对比验证Fig.4 Validation of discharge coefficient of choking and no-choking conditions

2 亚声速抽吸模型

亚声速流动和超声速流动有着本质的区别，二者的控制方程不同，分别是椭圆型方程和双曲型方程，使得亚声速抽吸模型处理起来和超声速模型有很大不同。

2.1 基于冲量定理的亚声速抽吸模型

基于冲量定理，从另一个角度建立亚声速抽吸模型。无穷远处均匀来流经过抽吸孔，抽吸孔处的扰动向流场上游传播，流线会逐渐向抽吸孔方向偏转，流动结构很复杂。从宏观的角度考虑，选取一个控制体，认为流动有两种状态：一种是在主流区域，速度方向平行于抽吸孔，另一种是经过等熵流动后抽吸腔背压所对应的状态，这两种状态的差别是由压差产生的冲量作用。

有如下关系式

(18)

则抽吸质量流率为

(19)

其中

(20)

式中M∞和Tb分别由等熵关系式(1)和式(3)确定。

由式(1)、式(3)、式(19)和式(20)可得出抽吸有质量流率为

(21)

流量系数为

(22)

式(22)是根据来流条件与背压条件确定的抽吸质量流率。通过Fluent数值模拟验证模型的有效性，选择均匀来流马赫数M∞=0.6，对比流量系数如图5所示。从图5以看出，整体来说模型比数值模拟结果偏小，模型在中高压比条件下和数值模拟结果基本一致，在低压比条件下和数值模拟结果有一定的差距。图6为图5的局部放大图，由图6可以看出，在低压比条件下流量系数变化非常小，表明亚声速抽吸也会发生壅塞现象，这是由于来流为亚声速的情况下，局部可以抽吸成超声速,但是对于亚声速来说需要很低的压比条件才可能发生壅塞。冲量模型没有考虑亚声速情况下抽吸孔对流场的扰动传播特性[18]。事实上，抽吸孔处的扰动可以向流场上游传播，扰动的叠加使得抽吸孔处的压力场近似为正余弦曲线的形式，因此模型和数值模拟结果具有一定的偏差。

图5 亚声速抽吸模型验证Fig.5 Validation of subsonic bleed model

图6 流量系数局部特征Fig.6 Local features of discharge coefficient

从图6可以发现流量系数有极值点，图6数值模拟结果也可以看出流量系数在一定的背压下不再变化，这是因为发生了抽吸壅塞。在来流条件一定的情况下，抽吸质量流率取决于背压，背压通过改变抽吸孔处的气流偏转角度进而改变抽吸质量流率。当压比小到一定程度时，抽吸孔处的气流在局部被抽吸成超声速，马赫数在垂直于抽吸孔方向上的分量为声速，扰动无法向上游传播，质量流率不再随压比的减小而改变，这是壅塞现象的物理机制。

2.2 亚声速抽吸数值拟合

根据冲量定理所得到的抽吸质量流率是假定流线垂直于抽吸孔，没有考虑亚声速流动中抽吸孔处的扰动向流场上游传播导致流线在抽吸孔处的偏转，仅仅考虑了初末两种状态的物理参数，只是一种宏观描述，而没有考虑流动的微观细节，这是冲量定理模型产生误差的原因。亚声速来流条件、抽吸孔前缘和后缘的扰动都可以影响到抽吸孔处的流动结构。在一定背压下，抽吸孔尺度范围内局部亚声速可以抽吸为超声速，涉及了跨声速问题，流场结构发生了本质的变化。从图6可以看出，与数值模拟结果相比，理论模型值在低压比时偏小，而在高压比时偏大，模型还有待进一步的完善。大量的数值模拟与参数分析表明亚声速抽吸质量流率为

(23)

即在压比和马赫数一定的情况下，质量流率和来流静压成正比，而和来流温度的平方根成反比。

根据式(9)和式(23)可知流量系数具有如下形式

(24)

Q=0.790 9-0.367 7x+0.625 6y+1.389x2-

0.128 9xy-2.227y2-1.593x3-1.186x2y-

0.373xy2+1.046y3

(25)

上式为拟合后的流量系数表达式，是一个关于压比和来流马赫数的三次多项式。为了检验数值拟合的准确性与有效性，选取不同的压比与来流马赫数，将Fluent数值模拟结果与数值拟合结果进行对比与验证，结果如表1中所示。

数值计算是Fluent基于Euler方程的结果，把计算流体力学(Computational Fluid Dynamics, CFD)计算结果作为标准，可以发现拟合结果和CFD结果基本一致，但是在高压比和高马赫数情况下，数值拟合结果和CFD计算结果稍有误差。因为在亚声速情况下，流量系数随压比和马赫的增加而减小，数据处理时，两个小量的比值由于很小的舍入误差就会导致流量系数的计算结果有比较大的误差。总体来说，数值拟合结果达到了一定的精度，可以作为亚声速抽吸流量系数的经验模型与数据库。

表1 亚声速抽吸模型验证Tab.1 Validation of subsonic bleed model

3 结论

本文根据超声速与亚声速流动的特征建立了二维抽吸孔模型，确定了壅塞发生时马赫数与压比满足的关系式，阐述了壅塞发生的物理机制，是一个基础性的工作，目的在于深刻认识抽吸流动的物理本质以及抽吸孔处的流动结构与流动特征，并发掘控制抽吸的关键因素。马赫波后的流动特征是超声速抽吸模型建立的切入点。亚声速流场的扰动向全流场传播，使得问题很复杂，但是仍然遵循基本的物理定律。流量系数的温度无关性表明在压比和马赫数确定的情况下，流量系数是不变的，这为抽吸模型在边界层中的进一步应用带来了很大便利。

抽吸是几何外形约束下的复杂流动。抽吸孔前缘可分为超声速前缘与亚声速前缘，遵循不同的抽吸流动机制。具有一定深度的抽吸孔会引入障碍激波而起到泄流作用，而且膨胀波与障碍激波会相互干扰。本文从复杂的抽吸装置中提取出决定抽吸质量流率的参数，建立抽吸质量流率模型，而把复杂抽吸系统的抽吸质量流率视为抽吸模型基础上各个因素的叠加后的结果，是为进一步建立三维圆孔抽吸流量模型奠定基础。下一步研究中，可以以二维抽吸模型为基础，以正多边形逼近圆孔，建立超声速三维圆孔抽吸模型。在抽吸孔具有一定深度的情况下研究压力波的传播与扰动机制[19]，建立湍流模式下的抽吸质量流率模型，研究抽吸对流场品质的影响，特别是抽吸对流向涡[20-21]的演化与发展的影响。