县级电力调度主变夏季最高负荷预测方法

（国网浙江海宁市供电有限公司，浙江 海宁 314400）

0 引言

负荷预测是电力调度、规划工作中必不可少的部分[1]，可分为长期预测（年度）、中期预测（月度）、短期预测（日）与超短期预测（小时）[2]。其中，长期、中期预测通常用于提供电源、电网规划基础数据，确定年度、月度检修计划、运行方式等；短期预测用于安排日开停机计划和发电计划；超短期预测用于实时安全分析、实时经济调度[2]。以上通常为省级及以上电力调度机构进行系统级负荷预测时的应用。在县级电力调度机构，负荷预测的范围及目的与系统级负荷预测不同：县级调度机构一方面需预测县域总负荷，支撑上级调度工作；另一方面需预测各主变的最高负荷，以便及时采取措施，防止出现主变过负荷运行情况。

在以往的负荷预测研究中，大多是基于系统级的研究，对于主变的负荷预测研究较少。系统级负荷预测的方法包括指数平滑法、支持向量机、小波变换、回归分析法等等[3-6]。与系统级负荷预测相比，主变负荷区域容量小，负荷随机性较大。因此，传统的系统级负荷预测方法对于主变负荷预测的适应性较差[6]。在浙江海宁地区，夏季通常为全年负荷最高的时期，部分变电站会出现主变过载的情况。为满足用户对供电可靠性及电能质量的要求，县级调度机构需要提高主变负荷预测的准确性，以便提前采取措施，减少主变过载造成用户停电的现象。本文研究的问题属于短期负荷预测，在参考系统级负荷预测方法的基础上，结合主变负荷特性，提出一种主变夏季最高负荷预测方法，考虑近几日气温变化和居民用电习惯变化，得出在一定置信度下主变最大负荷在特定温度下的波动区间。

1 主变夏季负荷特性

1.1 气温对主变负荷的影响

通常情况下，日负荷曲线具有明显的周期性，具体体现在[7]：不同日的日负荷曲线整体规律相似；同一星期类型日负荷规律相似；工作日、休息日负荷规律各自相似。主变负荷具有上述系统日负荷的所有特点。同时，受空调负荷影响，夏季负荷与气温存在较大关联。文献[8-9]分析夏季负荷与气温之间的关系，表明夏季日最大负荷与日平均气温、日最高气温、日最低气温变化趋势一致。文献[10]将温度分解为不同分量，提高夏季短期负荷预测精度。文献[11]提出一种考虑夏季气温累积效应的短期负荷预测方法。文献[12-15]研究夏季体感温度、人体舒适度对负荷的影响。

一般来说，夏季主变日最大负荷与当日最高温度呈正相关，并满足一定函数关系：

式中：PLj0表示当日主变j 的最高负荷；T0表示当日最高气温；Fj表示当日最高气温与主变j 最高负荷之间的函数关系。

但在高温天气开始的第一天，主变最高负荷往往低于持续高温下的最高负荷。这是由于室内温度变化滞后于气温变化，通常在高温天气刚出现时，空调负荷并不高，随着高温时间推移，负荷逐渐增加；同样，当持续高温后气温略有下降时，空调负荷往往高于相同温度下气温稳定时的空调负荷。这种负荷滞后于温度变化的现象为气温累积效应[11]。当最高气温高于38 ℃或低于28℃时，累积效应不明显[11]。因此，当最高气温处于28～38 ℃区间时，需考虑当日及3 日以内的最高气温。采用累积效应系数量化气温变化对主变最高负荷的影响，则主变j 的当日等效最高气温Teqj可表示为[11]：

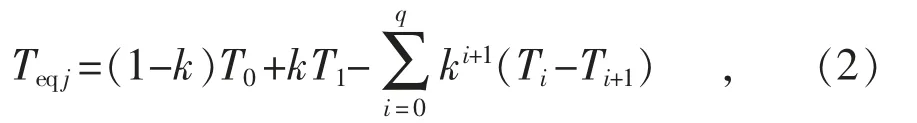
式中：T0表示预测当日的最高气温；Ti表示i 天前的最高气温；k 表示累积效应系数；q=min（n，3），n 表示日最高气温连续高于28 ℃的天数。则当日主变j 的最高负荷可表示为当日等效最高气温Teqj的函数关系式：

根据泰勒公式的基本原理，任意一个函数可拆分为近似于这个函数的多项式。综合考虑负荷预测的准确性与计算效率，将表示为关于Teqj的三次函数，即：

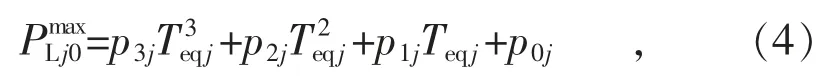
式中：p3j，p2j，p1j，p0j分别为主变j 的负荷系数。

1.2 主变负荷的不确定性

在系统级负荷预测中，由于供电区域大，电力负荷高，每个电力用户的用电情况对系统总负荷的影响很小，其中一些用户用电量增加，可能另一些用户用电量降低，系统负荷比较稳定。而在主变负荷预测中，一个大用户的用电情况改变可能会对主变负荷造成较大影响，主变负荷预测的准确率一般低于系统负荷预测的准确率。因此，仅仅给出一个不是很准确的预测值对于实际工作的意义不大。为了更好地在实际工作中加以应用，考虑将预测值替换为预测区间，即预测出等效最高气温下主变最高负荷的波动区间。则主变j 在等效最高气温Teqj下的最高负荷波动区间为，且满足：

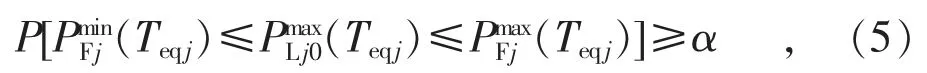
式中：α 为主变j 在等效最高气温Teqj下的最高负荷落在区间的置信度水平。

2 主变夏季最高负荷预测方法

为预测主变夏季最高负荷，首先需要收集、筛选具有参考意义的主变负荷数据，然后求取主变负荷系数、累积效应系数和夏季等效气温偏移量，最后分析主变最高负荷的波动范围。

2.1 收集、筛选主变负荷数据

在本文中，只研究晴好天气下工作日的主变负荷预测。收集预测日前若干天的主变负荷情况和最高气温，并将法定节假日及主变供电区域发生变化时的负荷数据剔除。此外，由于海宁地区光伏发电渗透率高，日负荷受日照强度影响较大，且阴雨天气会导致体感温度降低，也需将阴雨天气下的负荷数据剔除，并将收集到的负荷数据分为前M 日和后N 日两部分。其中，前M 日包含的最高气温的变化范围应尽可能广，使f（P，T）三次函数曲线拟合尽可能准确。

2.2 确定主变负荷系数与累积效应系数

本文中需求取主变负荷系数与累积效应系数，具体方法如下：

（1）应用MATLAB 中的最小二乘法求解前M日主变负荷与当日最高温度的函数关系f（P，T）。

（2）对不同温度下的累计效用系数k 进行离散化处理，并将式（2）代入f（P，T），得到f（ki，T），应用最小二乘法，求出使f（ki，T）的残差函数最小的累计效用系数k[11]。从而得出前M 日每一日的等效最高气温以及主变负荷系数。

2.3 求取夏季等效气温偏移量

在高温天气开始的一段时间内，人们往往较能忍耐，空调负荷较低；随着高温天气的持续，很多人会形成开空调的习惯，主变空调负荷随之上升。因此，在夏季的不同阶段，即使由式（2）确定的等效最高气温相同，主变最高负荷往往存在差异。为量化这种差异，本文引入等效气温偏移量的概念，表示夏季不同阶段的负荷差异等效体现在温度上的变化。由于不同主变的负荷性质不同，各主变的等效气温偏移量也不相等。若主变j后N 日在等效最高气温Teqj下的负荷与前M 日等效最高气温为（Teqj+dTj）时近似，则dTj表示主变j 的等效气温偏移量。求解等效气温偏移量的具体方法为：将T=T+dT 代入f（P，T），得到f（P，T+dT），并调整dT 的值，使f（P，T+dT）的残差函数最小。此时的dT 值即为该主变的等效气温偏移量。

2.4 分析主变最高负荷波动范围

经过2.2 节与2.3 节的分析与计算，已得出主变负荷系数、累积效应系数和夏季等效气温偏移量。由于后N 日和预测日相隔更近，因此应通过分析后N 日预测值误差的情况确定主变最高负荷的取值范围。预测值误差应满足期望为0 的正态分布。设后N 日主变最高负荷预测值误差的标准差为sNj，则在置信度水平为α 的情况下，等效最高气温Teqj下的主变最高负荷的变化范围为[Fj（Teqj）-mαsNj，Fj（Teqj）+mαsNj]。其中，mα的取值可通过正态分布基本特性确定。最后，根据主变历史负荷，对个别等效最高气温下的负荷预测值进行修正。

3 算例分析

为验证主变最高负荷预测方法的可行性，采用本文所述方法，对位于浙江海宁西部的许巷变1 号主变及2 号主变夏季最高负荷进行预测。

收集2019 年7 月1 日—8 月20 日的负荷数据，将7 月1 日—8 月10 日作为前M 日，将8 月11 日—8 月20 日作为后N 日，预测8 月21 日、8 月22 日、8 月26 日、8 月27 日、8 月30 日2台主变的最高负荷（8 月下旬其他日期不满足晴好天气工作日标准）。应用第2 节所述方法，计算出各主变负荷系数与等效气温偏移量如表1 所示。

表1 许巷变主变负荷系数与体感温度差

取置信度水平α=90%，则mα=1.65。根据表1所列参数，能够得出许巷变1 号主变和2 号主变最高负荷的变化区间。

图1、图2 中的实线与虚线分别表示预测出的1 号主变与2 号主变最高负荷的上限与下限，实际最高负荷落在此区间的概率不小于90%。图1、图2 中的圆点分别表示1 号主变与2 号主变在8 月21 日、8 月22 日、8 月26 日、8 月27日、8 月30 日的实际最高负荷。可见，实际负荷值均落在预测区间，证明了本文所述主变负荷预测方法具有可行性。

4 结语

目前，负荷预测的相关研究主要集中在系统级，针对主变的负荷预测研究较少。本文在系统级负荷预测研究的基础上，结合主变负荷特性，考虑气温和居民用电习惯变化对主变负荷的影响，提出了一种预测主变最高负荷的方法。在算例分析中，主变实际最高负荷与应用该方法预测出的最高负荷波动区间相符，证明了该方法的可行性。

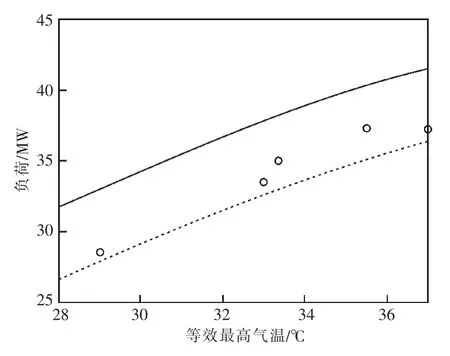
图1 许巷变1 号主变负荷情况

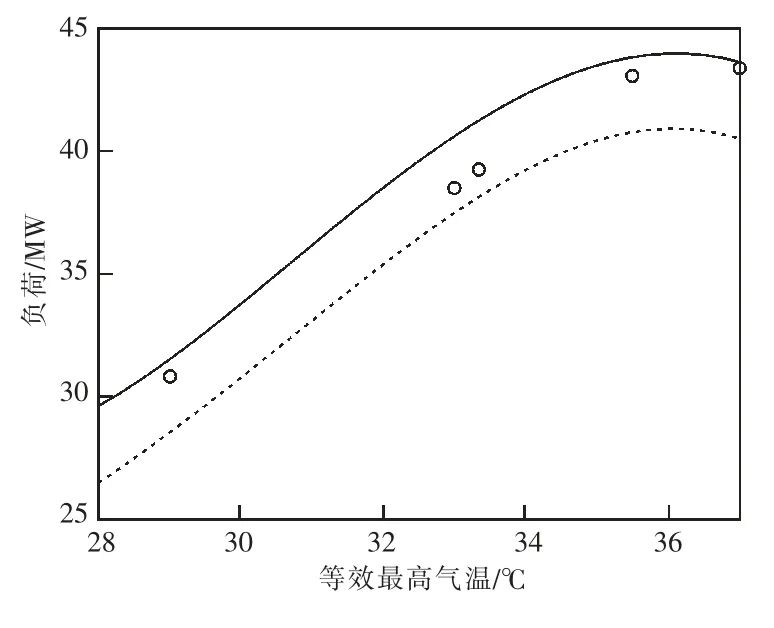
图2 许巷变2 号主变负荷情况