基于扩展正交迭代的快速加权的相机位姿估计

王世安，王向军，阴 雷

〈系统与设计〉

基于扩展正交迭代的快速加权的相机位姿估计

王世安，王向军，阴 雷

（天津大学 精密测试技术及仪器国家重点实验室，天津 300072）

相机位姿估计算法多基于参考点而较少利用图像中的直线信息，本文对于相机位姿估计算法的抗干扰性和实时性，在扩展正交迭代的基础上，提出了一种基于点和直线段结合的快速加权的相机位姿估计算法，该算法以加权共线性误差和加权共面性误差之和为误差函数，根据计算初值的深度信息和重投影误差确定权重系数，并对整体进行加速优化，将每次迭代计算的时间复杂度从()降到了(1)。仿真实验结果表明算法可以抑制异常点的干扰，减少计算时间，旋转矩阵计算误差比传统正交迭代算法减少48.31%，平移向量计算误差减少48.79%，加速优化后的计算时间为加速前的47.11%。实物实验表明该算法可以充分利用检测到的参考点和参考直线信息，提高计算精度，有较高的实际应用价值。

机器视觉；图像处理；位姿估计；迭代算法；计算复杂度

0 引言

相机位姿估计问题是摄影测量学[1]、计算机视觉[2]、计算机图形学[3]以及机器人科学[4]的一个重要问题，在无人平台导航[5]、航天器对接[6]、相机标定[7]、增强现实[8]等领域有广泛应用。位姿估计问题根据相对应特征信息的不同可以分为3类[9]：2D-2D位姿估计、2D-3D位姿估计、3D-3D位姿估计。其中2D-3D位姿估计问题又叫做点透视问题（PnP，Perspective-n- Point）。

目前在PnP问题的迭代算法中，文献[10]提出的正交迭代算法计算精度高，迭代次数少，计算速度快并且有全局收敛性。直线作为特征点之外易于获取且较为稳定的几何特征在位姿估计中可以提高算法精度和鲁棒性，并且在缺少纹理、图案重复的情况下可以起到主导作用[11]。此外在复杂真实环境中进行实时位姿估计时，由于测量误差难免会产生异常数据，正交迭代算法的计算结果会有较大偏差。本文对于文献[12]提出的基于点和直线段对应的扩展正交迭代算法进行了优化，通过初值得到普通特征点和直线段上特征点的深度和重投影误差，通过初值的深度信息和重投影误差确定物方空间误差的权重系数，并根据文献[13]提出的思想，提出了在点和直线段对应情况下的快速加权正交迭代算法，将算法迭代时的计算复杂度从()降低到(1)，在提高计算速度的同时，提高了算法的抗干扰能力和旋转矩阵、平移向量的计算精度，并可以克服场景中缺少特征点的情况。

1 基于点和直线段结合的快速加权正交迭代算法

1.1 扩展正交迭代算法

正交迭代算法[10]计算参考点的共线性误差，并以此作为迭代计算的误差函数，即：

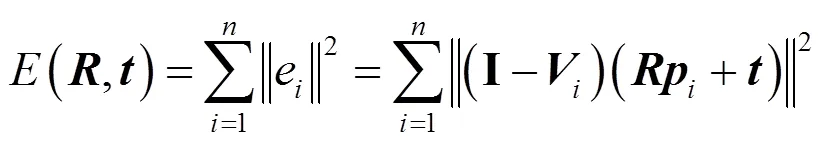
令v为参考点在归一化平面上的投影，则公式中为单位矩阵；＝T/(T)为视线投影矩阵；为旋转矩阵；为平移向量，且旋转矩阵为正交矩阵，有T＝。

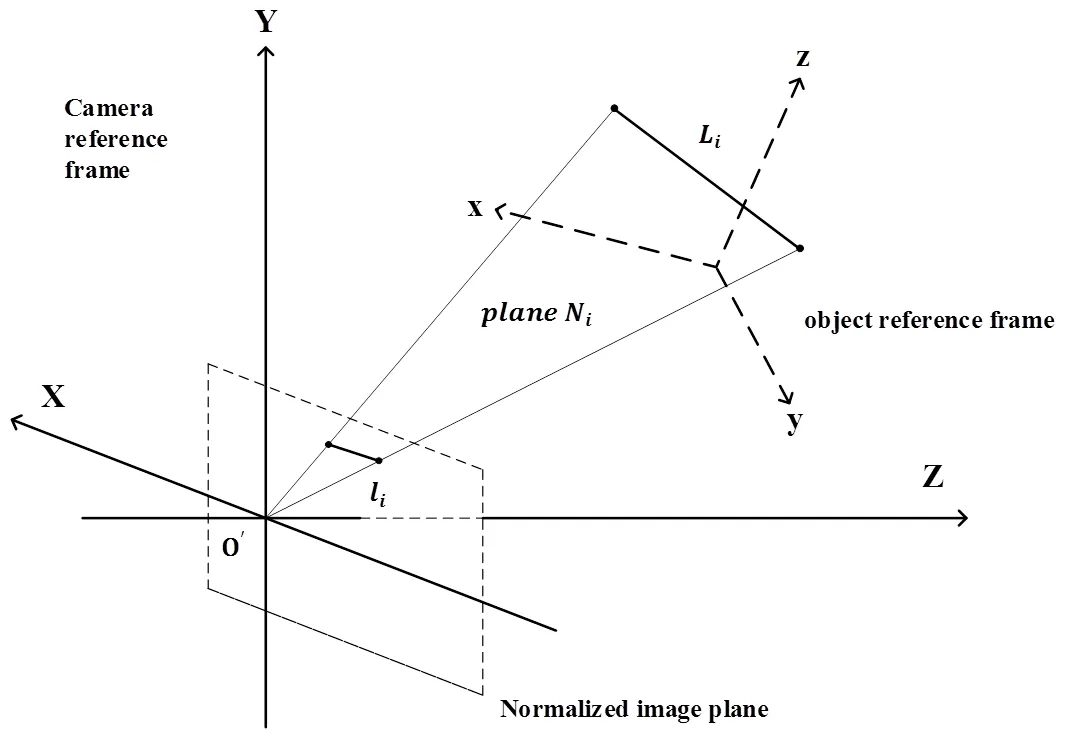
图1 物体空间和归一化平面上的对应直线段

图2 物体空间的共面性误差

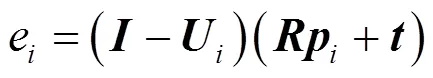
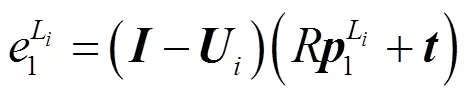
则将直线段L在物体空间的误差的平方定义为其两个端点的共面性误差的平方之和：

设位姿估计前可以提取到个参考点(1,2, …,p)和个参考直线段(1,2, …,L)，则扩展正交迭代算法的目标函数为：

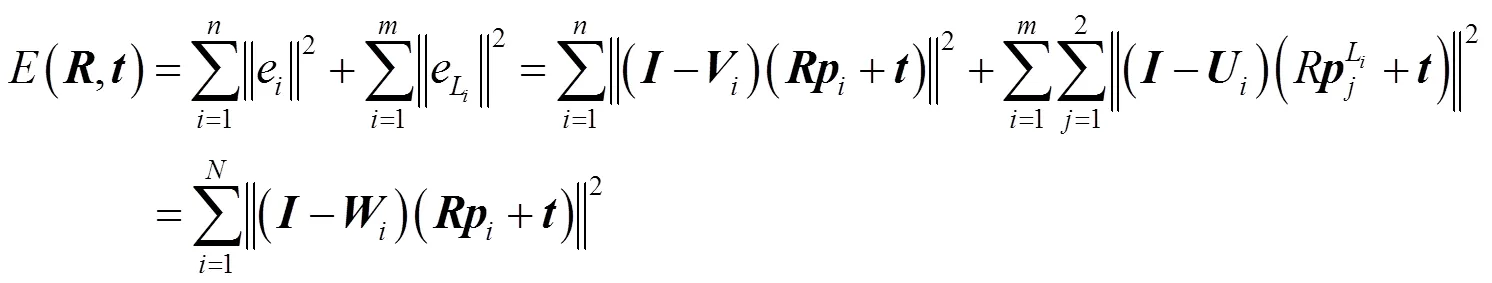
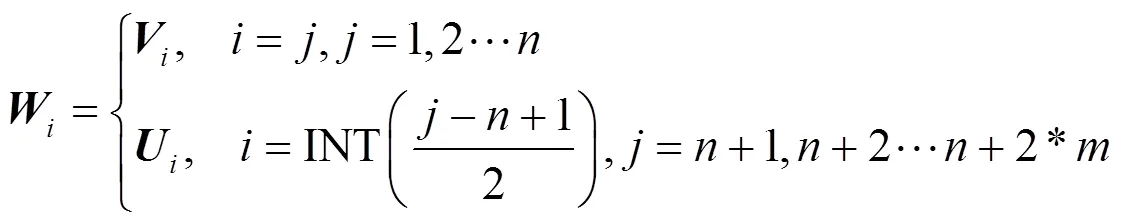
式中：＝＋2*，T＝，INT表示取整数。

1.2 加权扩展正交迭代

1.2.1 加权扩展正交迭代算法

扩展正交迭代对于每一个参考点和每一条检测到的直线段都赋予相同的权重，然而对于在相机坐标系中不同深度的参考点和直线段，这样显然无法得到最高的精度。此外在很多情况下个别的异常参考点（包括参考直线段的端点）会有较大的测量误差，在实际应用中这种难以避免的误差会较大地影响位姿估计算法的计算精度。因此可以对不同的参考点和直线段加入不同的权重系数，以提高计算精度避免异常点的影响。加入权重系数以后的目标函数如下：

式中：＞0为第个参考点（包括直线段的两个端点）的权重系数。加入权重后，当给定第次对于的估计值(k)以后，可以得出此时的最优值为：

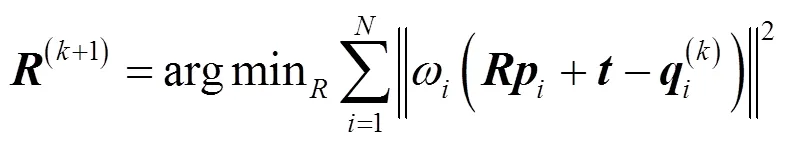
1.2.2 权重系数确定方法

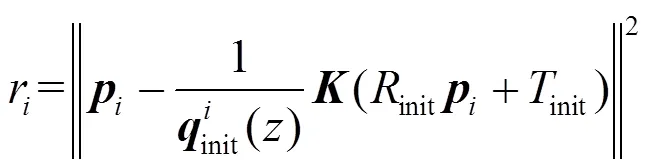
式中：为相机内参矩阵。

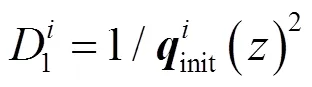
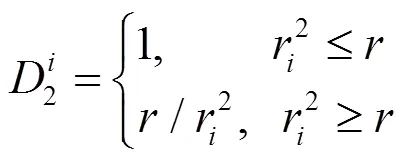
式中：为r2的均值。由此可以得到既考虑了参考点深度又考虑了初始值的重投影误差的权值：

1.3 快速加权扩展正交迭代

正交迭代算法作为非线性PnP算法计算时间较长，在对每个参考点加入权值以及扩展到直线段以后又增加了较大的计算量，计算消耗时间进一步增加，本文通过将迭代算法公式中的矩阵拉直，并通过整合使加权扩展正交迭代算法每次迭代的计算复杂度从()降到了(1)，具体推导过程如下：

首先引入公式：

式中：vec表示以列为单位把一个矩阵排为一个列向量，称为矩阵的拉直：Ä表示克罗内克积（Kronecker product）。对式(9)做拉直运算得：

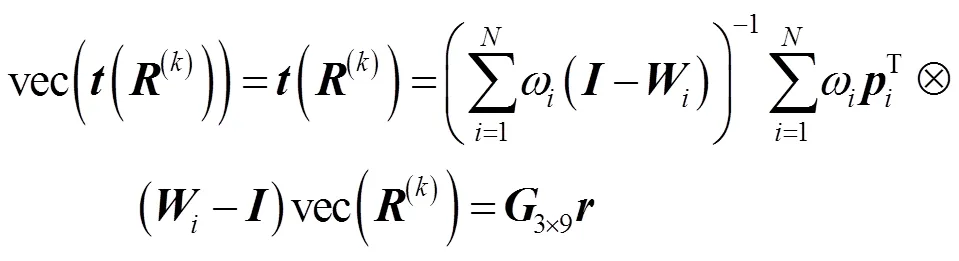
式中：

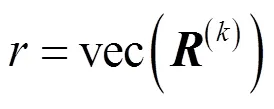
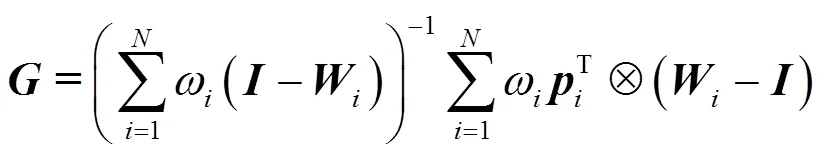
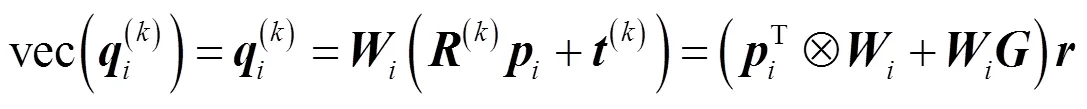
进一步可得：

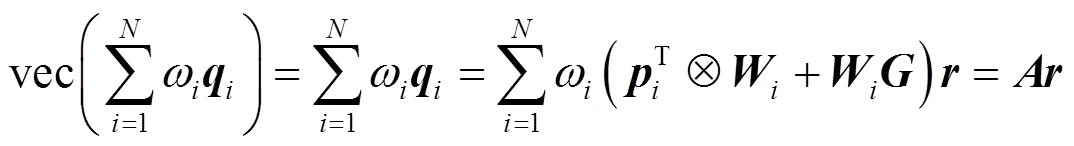
式中：

整理公式得：

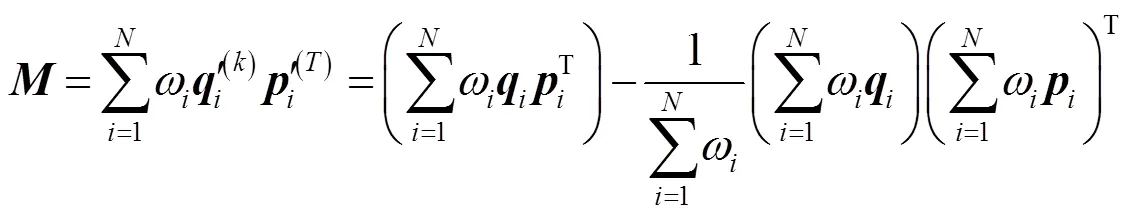
对进行拉直运算可以得到：

式中：

因此可以得到，对进行奇异值分解（SVD）即可得到(k＋1)。

在每次迭代过程中对误差函数进行规整可得：

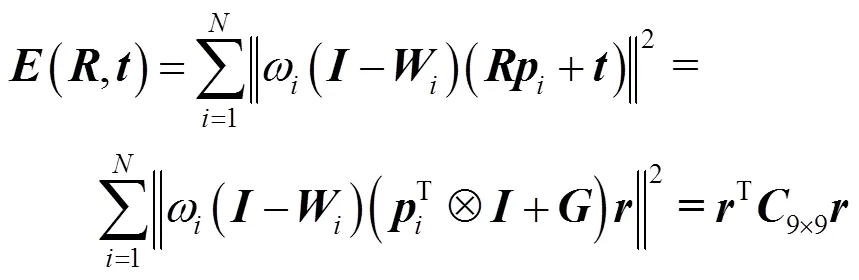
式中：

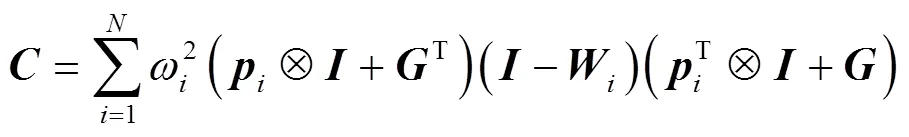
经过对、和(,)进行拉直运算后，将每次迭代的变量提取出来，可以在迭代前只计算一次、和C，计算复杂度均为O()，在迭代时只需与拉直后的相乘，计算复杂度为O(1)，从而可以极大地减少加权扩展正交迭代算法的计算时间，增强算法的实时性。

2 实验

为了验证本文提出的快速加权的扩展正交迭代算法的正确性和有效性，我们进行了相机位姿估计的matlab数值仿真实验和实物实验，分别比较以下9种算法的计算误差和消耗时间：（1）RPnP：[15]提出的RPnP算法；（2）OPnP：[14]提出的OPnP算法；（3）LHM：[10]提出的以弱透视模型（Weak Perspective Approximation）为初值的正交迭代算法；（4）RPnP/OPnP＋LHM：使用RPnP和OPnP算法按照1.2.2小节的方式计算迭代算法的初值，然后使用正交迭代算法；（5）RPnP/OPnP＋ELHM：使用上述初值，然后使用[12]提出的扩展正交迭代算法；（6）RPnP/OPnP＋D1＋ELHM：使用上述初值，然后使用只考虑深度信息的加权扩展正交迭代；（7）RPnP/OPnP＋D2＋ELHM：使用上述初值，然后使用只考虑投影误差的加权扩展正交迭代；（8）RPnP/OPnP＋W＋ELHM：使用上述初值，然后使用考虑两种权重系数的加权扩展正交迭代；（9）RPnP/OPnP＋W＋ELHM＋：使用上述初值，然后使用经过加速运算的快速加权扩展正交迭代。

2.1 仿真实验

仿真实验使用的虚拟相机的参数：分辨率为640×480，等效焦距为800pixel，参考点和参考直线段的端点随机分布在[－2,2]×[－2,2]×[4,8]的空间中。仿真实验中每次随机产生3个欧拉角并将其转换成旋转矩阵，在[－50,50]×[－50,50]×[0,100]的范围内随机产生平移向量，并将点投影在图像上后加入期望为0，标准差为的高斯噪声。对于旋转矩阵，由于欧拉角的万向锁问题（Gimbal Lock），实验中将旋转矩阵转换成四元数来表示姿态，令旋转矩阵真值转换成为四元数，计算得到的旋转矩阵转换¢成为四元数¢，定义旋转矩阵的相对误差为()＝(－¢)2/2。对于平移向量，令平移向量真值为，计算得到的平移向量为¢，定义平移向量的相对误差为()＝(－¢)2/2。

2.1.1 参考点数目实验

参考点数目实验（研究存在异常参考点时算法计算精度和参考点数目的关系）：参考点数目从4增加到12，参考直线数目为2，随机一个参考点加上为5pixel的高斯噪声，其余参考点加上为0.5pixel的高斯噪声。对于不同的参考点数目都进行1000次独立重复试验。实验结果如图3所示。

从图3可以看到在有异常点和相同的初始值的情况下，加权扩展正交迭代算法对于旋转矩阵和平移向量的计算精度，相比于扩展正交迭代和正交迭代算法有较大提高并且保持在较高的水平。

2.1.2 异常点和高斯噪声实验

异常点和高斯噪声实验（研究存在异常参考点时算法计算精度和高斯噪声的关系）：参考点数目固定为10，参考直线数目为2，高斯噪声标准差统一从1pixel增加到10pixel，每次随机选择一个参考点加上标准差为当前标准差5倍的高斯噪声。对于不同的标准差都进行1000次独立重复试验。实验结果如图4所示。

从图4可以看到随着高斯噪声水平的增加，加权扩展正交迭代的计算精度始终最高，相比于没有考虑加权系数的扩展正交迭代有较大提高。同时可以看出只考虑深度信息的加权扩展正交迭代计算精度高于没有加权的扩展正交迭代，只考虑初始值的重投影误差的扩展正交迭代对异常点的抗干扰性较强。

2.1.3 平移距离实验

平移距离实验（研究存在异常点和高斯噪声时计算精度和平移距离的关系）：固定参考点数目为10，参考直线数目为2，随机一个参考点加上为10pixel的高斯噪声，其余参考点加上为1pixel的高斯噪声，令平移向量和在[－20, 20]（步长5乘上参考点区域大小4）的区域内随机产生，令参考点区域到相机距离与参考点区域大小之比/4以步长为5从5增加到40，每次做1000次独立重复性实验，实验结果如图5所示。

图3 参考点数目增加时，旋转矩阵和平移向量的相对计算误差

图4 高斯噪声水平增加时，旋转矩阵和平移向量的相对计算误差

从图5可以看到随着距离的增加，加权扩展正交迭代的计算精度始终最高，且受距离的影响较小。

2.1.4 计算时间实验

计算时间实验（研究算法的计算速度随参考点数目的变化）：参考点数目从4增加到104，参考直线数目为2，在参考点上加上标准差为3pixel的高斯噪声，计算1000次独立重复试验算法消耗时间的平均值，实验结果如图6所示。

从图6可以看出，没有加速的加权扩展正交迭代的计算时间远多于扩展正交迭代和正交迭代算法，而加速后的加权扩展正交迭代算法则大量节省了计算时间，大约可以减少40ms。在参考点增多以后，因为需要对每个参考点和参考直线段端点加以权重的原因，计算时间会多于没有加速的正交迭代算法，但是少于没有加速的加权正交迭代。

2.2 实物实验

在真实图像实验中，使用KITTI[16]（Karlsruhe Institute of Technology and Toyota Technological Institute at Chicago）标准数据集对PnP算法进行验证。KITTI数据集是由德国卡尔斯鲁勒理工学院搭建，包括了城市、乡村、高速公路等多种环境，通过自主驾驶汽车进行采集，车上载有多种传感器，其中高精度的组合导航系统为数据集提供相机位姿真值。数据集中的图片分辨率为1226pixel×370pixel，相机等效焦距为707.0912pixel。

在实验中首先对序列图片进行特征点匹配和直线段匹配，直线段检测使用LSD[17]算法（line segment detector），得到特征点和直线段端点的坐标，其中直线匹配结果如图7所示。

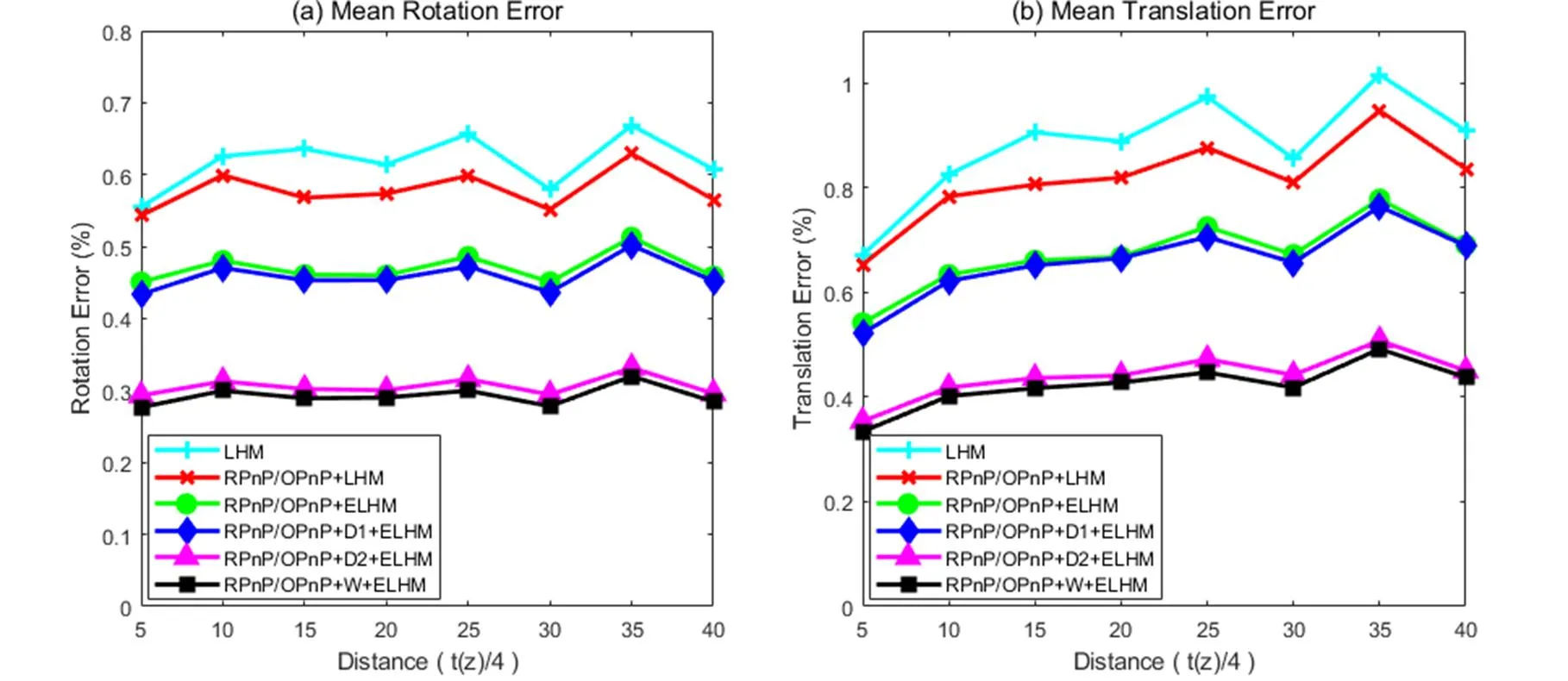
图5 相机与参考点区域距离增加时，旋转矩阵和平移向量的相对计算误差

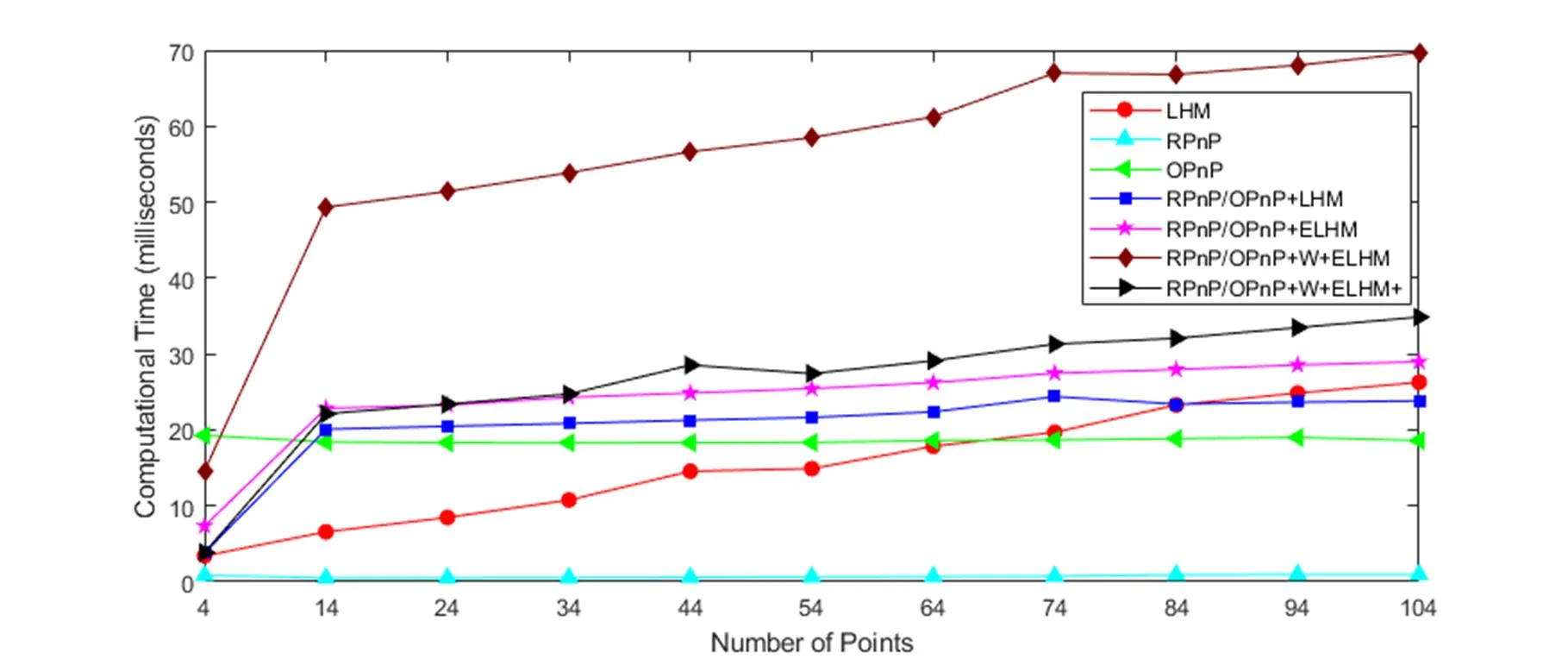
图6 参考点数目增加时，各种算法的计算时间对比

初始化时通过对极几何计算第一帧和第二帧之间的旋转和平移矩阵，通过三角化计算匹配的特征点和直线端点的三维坐标，然后利用三维坐标和特征点和直线段点在下一帧的二维坐标计算相机的旋转和平移。初始化后则直接利用上一次PnP算法计算的旋转和平移矩阵，通过三角化来计算三维坐标以进行下一次的PnP。实验结果如图8，9所示。

从图8，9中可以看到在序列图片实验中本文提出算法的计算误差远小于传统正交迭代算法的误差，计算准确性较高。由于直线提取以及匹配的不稳定性，在个别图像中加速加权扩展正交迭代算法的计算误差大于传统正交迭代算法，但是仍保持在较低水平，并且这种情况出现的次数较少，不影响整体计算的准确性。在序列图像中的实验证明了提出的算法有较高的准确性和鲁棒性，充分利用了图像中的信息，在实际场景应用中有较高价值。

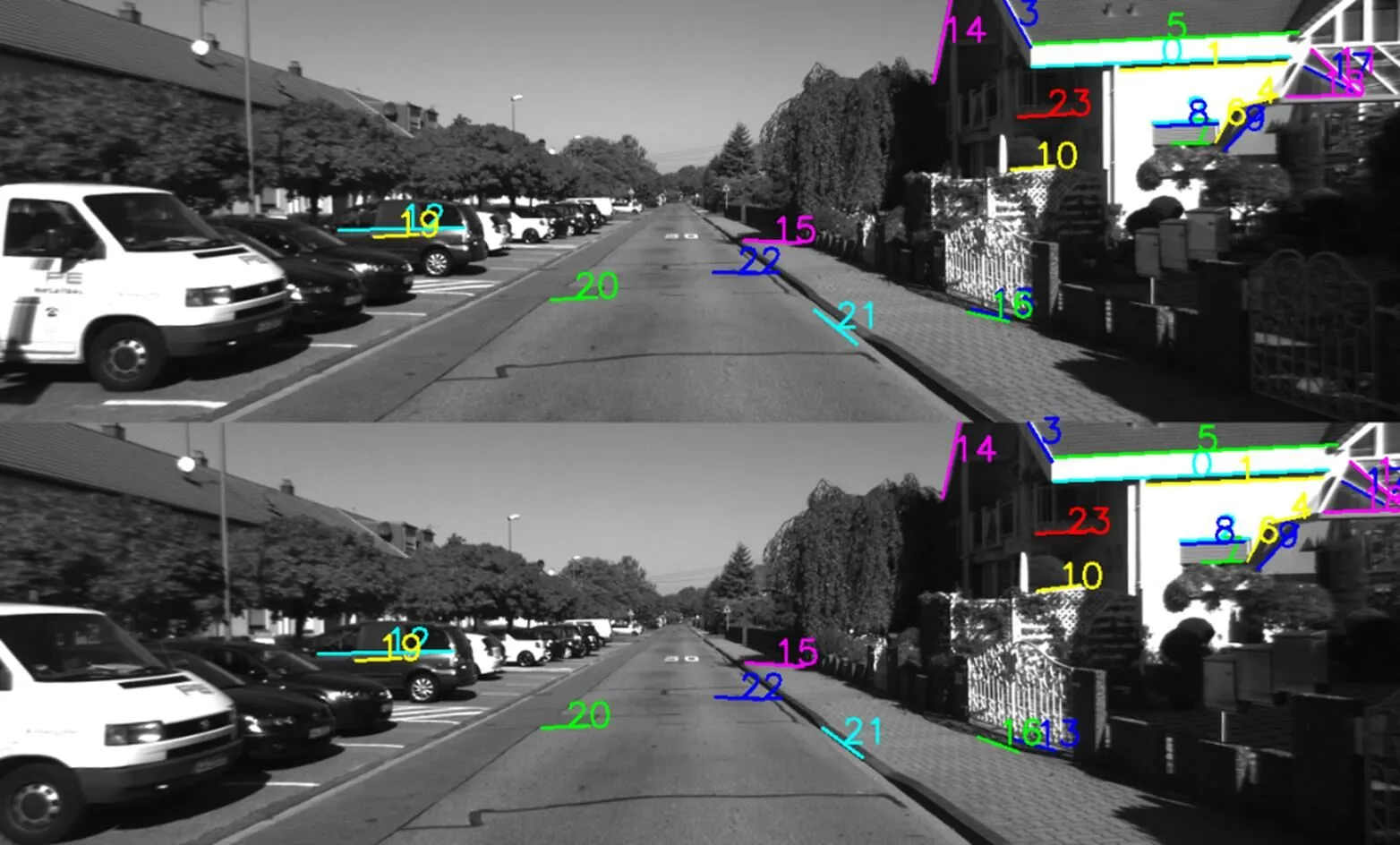
图7 序列图像直线匹配结果，相匹配的直线用同样的颜色和相同的序号标注

图8 序列5中旋转矩阵和平移向量的计算误差

图9 序列6中旋转矩阵和平移向量的计算误差

由于在序列图片中每次进行位姿估计时，需要根据上一次的计算结果来使用PnP算法计算本次的位姿，使用快速加权扩展正交迭代算法会有一定的累积误差，但是由于提取了序列图片中的直线信息并且对参考点和线段端点加以权重，该算法的累积误差远小于传统的正交迭代算法的累积误差。对于位姿计算实验中的累积误差，可以使用光束平差法[5]对位姿进行优化从而抑制累积误差，同时可以使用回环检测[5]的方法对位姿进行优化，从而在一定程度上消除累积误差。

3 结论

针对二维—三维特征对应（2D-3D）的相机姿态估计算法（PnP）进行了研究，在基于点和直线段的扩展正交迭代算法的基础上提出了快速加权扩展正交迭代算法。该算法可以利用图像中的直线信息，既考虑了参考点以及参考直线端点的深度信息，又考虑了参考点和参考直线端点的重投影误差，并通过公式推导将每一次迭代的时间复杂度从()降到了(1)，从而提高了算法的计算精度和计算速度。

数值仿真实验和真实图片实验，对所提出的位姿估计算法进行了验证，并与正交迭代算法和扩展正交迭代算法进行对比，结果证明该算法有效地提高了计算精度、计算速度，对异常点有较强的抗干扰能力，对复杂环境下的实时相机姿态估计问题具有一定价值。

[1] Mullen R.[M]. Barlow: Asprs Publications, 2004.

[2] Hartley R, Zisserman A.[M]. Cambridge: Cambridge university press, 2003.

[3] Gingold Y, Igarashi T, Zorin D. Structured annotations for 2D-to-3D modeling[C]//()., 2009, 28(5): 148.

[4] DeSouza G N, Kak A C. Vision for mobile robot navigation: A survey[J]., 2002, 24(2): 237-267.

[5] Mur-Artal R, Montiel J M M, Tardos J D. ORB-SLAM: a versatile and accurate monocular SLAM system[J]., 2015, 31(5): 1147-1163.

[6] 钱萍, 王惠南. 基于对偶四元数的航天器交会对接位姿双目视觉测量算法[J]. 宇航学报, 2013, 34(1): 32-38.

QIAN Ping, WANG Huinan. A Binocular Vision Algorithm Based on Dual Quaternion for Relative Position and Attitude Determinati of RVD Spacecrafts[J]., 2013, 34(1): 32-38.

[7] 吴凡路, 刘建军, 任鑫, 等. 基于圆形标志点的深空探测全景相机标定方法[J]. 光学学报, 2013, 33(11): 1115002.

WU Fanlu, LIU Jianjun, REN Xin, et al. Deep space exploration panoramic camera calibration technique basedon circular markers[J]., 2013, 33(11): 1115002.

[8] Azuma R, Baillot Y, Behringer R, et al. Recent advances in augmented reality[J]., 2001, 21(6): 34-47.

[9] Haralick R M, Joo H, Lee C N, et al. Pose estimation from corresponding point data[J]., 1989, 19(6): 1426-1446.

[10] LU C P, Hager G D, Mjolsness E. Fast and globally convergent pose estimation from video images[J]., 2000, 22(6): 610-622.

[11] Pumarola A, Vakhitov A, Agudo A, et al. PL-SLAM: Real-time monocular visual SLAM with points and lines[C]//2017()., 2017: 4503-4508.

[12] 许允喜, 蒋云良, 陈方. 基于点和直线段对应的扩展正交迭代位姿估计算法[J]. 光学学报, 2009(11): 3129-3135.

XU Yunxi, JIANGYunliang, CHEN Fang. An Extended Orthogonal Iteration Algorithm for Pose Estimation from Point and Line Segment Correspondences [J]., 2009, 29(11): 3129-3135.

[13] 周润, 张征宇, 黄叙辉. 相机位姿估计的加权正交迭代算法[J]. 光学学报, 2018, 38(5): 0515002.

ZHOU Run, ZHANG Zhengyu, HUANG Xuhui. Weighted Orthogonal Iteration Algorithm for Camera Pose Estimation[J]., 2018, 38(5): 193-199.

[14] ZHENG Y, KUANG Y, Sugimoto S, et al. Revisiting the pnp problem: A fast, general and optimal solution[C]//, 2013: 2344-2351.

[15] LI S, XU C, XIE M. A robust O (n) solution to the perspective-n-point problem[J]., 2012, 34(7): 1444-1450.

[16] Geiger A, Lenz P, Stiller C, et al. Vision meets robotics: The KITTI dataset[J]., 2013, 32(11): 1231-1237.

[17] VonGioi R G, Jakubowicz J, Morel J M, et al. LSD: A fast line segment detector with a false detection control[J]., 2008, 32(4): 722-732.

Accelerativeand Weighted Camera Pose Estimation Based on Extended Orthogonal Iterative Algorithm

WANG Shi’an，WANG Xiangjun，YIN Lei

(State Key Laboratory of Precision Measurement Technology and Instruments, Tianjin University, Tianjin 300072, China)

The camera pose estimation algorithm is typically more based on reference points and less on the linear information in the image. In this paper, based on the extended orthogonal iteration, an accelerative and weighted camera pose estimation algorithm based on the combination of point and line segments is proposed to ensure a good anti-interference and real-time performance of the algorithm. The algorithm considers the sum of the weighted collinearity error and the weighted coplanarity error as the error function. The weight coefficients are determined by the depth information and the re-projection error of the initial value. In addition, the algorithm accelerates the iterative process and reduces the time complexity of the iteration process dramatically from() to(1). The simulation results demonstrate that the algorithm can suppress the interference of abnormal points and reduce the calculation time. The calculation accuracy of the rotation matrix is 51.69% higher than that of the traditional orthogonal iterative algorithm, and the calculation accuracy of the translation vector is increased by 51.21%. Furthermore, the calculation time after the acceleration is reduced by 47.11%. The physical experiment shows that the algorithm can make full use of the detected reference points and reference line information, improve the calculation accuracy, reduce the cumulative error, and has high practical application value.

machine vision, image processing, pose estimation, iterative algorithms, computational complexity

TP391

A

1001-8891(2020)05-0205-08

2019-10-09；

2020-02-27.

王世安（1995-），男，硕士，主要研究方向为计算机视觉和图像处理。E-mail：sean_wang@tju.edu.cn。