微光ICCD相机的动态调制传递函数理论模型研究

韩 坤，姚 泽，乔 凯，杨书宁，贺英萍

〈微光技术〉

微光ICCD相机的动态调制传递函数理论模型研究

韩 坤1,2，姚 泽1,2，乔 凯1,2，杨书宁1,2，贺英萍1,2

（1. 微光夜视技术重点实验室，陕西 西安 710065；2. 昆明物理研究所，云南 昆明 650223）

在微光像增强型电荷耦合器件（Intensified Charge-coupled Device，ICCD）积分时间内，空间振动影响微光ICCD相机的成像，导致成像质量下降。对于振动环境下微光ICCD相机成像，采用动态调制传递函数（modulation transfer function，MTF）评价空间振动对成像质量影响。结合微光ICCD相机特有结构，提出微光ICCD相机的动态MTF理论模型，分析低频正弦振动及高频正弦振动中，振动幅度、振动周期、积分时间等不同因素对成像质量的影响。

微光ICCD相机，动态调制传递函数，正弦振动

0 引言

微光像增强型电荷耦合器件由微光像增强器（Low light image intensifier）和电荷耦合器件（Charge-coupled Device，CCD）通过光学纤维面板或中继透镜耦合而成，其中微光像增强器通过光电转换、电子倍增实现微光条件下光电成像；CCD相机将光信号转换为模拟电流信号，通过放大和模数转换实现图像获取、存储传输、处理和复现[1-2]。微光ICCD相机结合了两大成像器件的技术优势，实现微光条件下视频采集、图像拍照等功能，结合软件可对输出数字信号进行处理，提高输出图像质量。

调制传递函数是评价成像器件的成像质量的一个综合性参考因素[3]。其中，高频空间频率范围的MTF反映物体的细节还原能力，中频空间频率范围的MTF反映物体的层次还原情况，低频空间频率范围的MTF反映物体的轮廓还原情况。车载或机载微光ICCD相机在拍照中，由于相机本身的震动、外部环境（地面、气流）引起的振动会影响相机的成像质量，图像的分辨率会下降。基于静态空间MTF提出的动态MTF能客观地反映振动对相机成像质量的影响[4]，目前关于动态MTF的研究大多集中在日间航空相机方面，微光ICCD相机的动态成像质量研究还没有展开。

本文基于静态空间MTF理论，针对正弦振动，采用动态MTF概念开展研究，准确地提出微光ICCD相机的动态MTF理论模型，以评价振动对微光ICCD相机的成像质量的影响。

1 微光ICCD相机工作原理

本文主要研究双近贴式三代微光像增强器与CCD传感器通过纤维光锥耦合的微光ICCD相机，组成结构图如图1所示，主要由光学成像系统（Imaging system）、微光像增强器、纤维光锥（Fiber optic taper）、CCD传感器等部件组成；微光像增强器主要由输入窗（Input window）、GaAs光阴极（Photocathode）、防离子反馈膜（Ion barrier film）、微通道板（Microchannel plate，MCP）、荧光屏（Fluorescent screen）、高压电源（High-voltage power source）及灌封壳体（Potting shell）等部件组成；光阴极及微通道板之间为前近贴（Front proximity）电子光学系统微通道板及荧光屏之间为后近贴（Back proximity）电子光学系统。

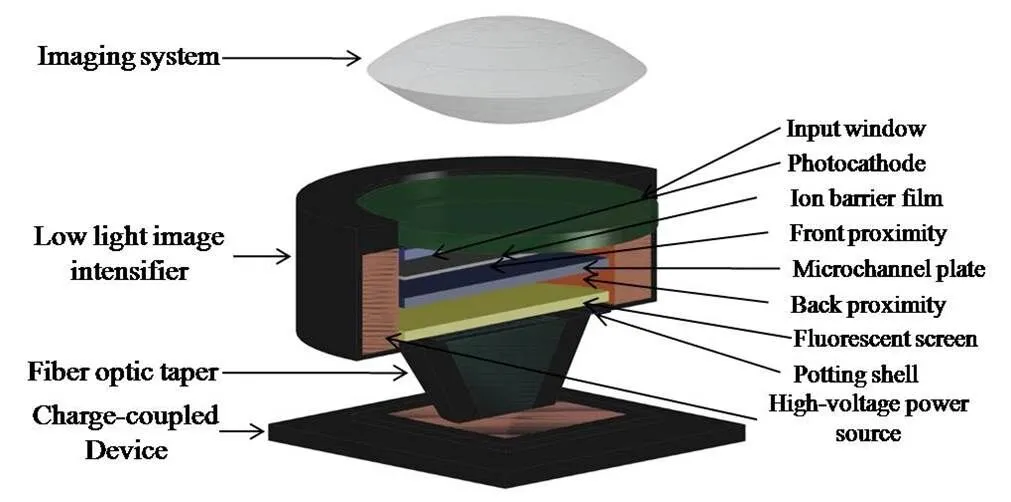
图1 纤维光锥耦合式微光ICCD相机结构图

ICCD器件模型的耦合方式采用文献[5]及[6]中的方法，其存在两种耦合界面：①光锥输出端面与光学粘结剂之间的界面；②光学粘结剂与CCD光敏面之间的界面；文献[6]中指出ICCD相机耦合前后分辨率基本一致，可忽略耦合界面影响。

微光ICCD相机工作原理如图2所示，整个过程为：①微光环境下的实物通过成像系统输出光学图案至光阴极；②GaAs光阴极完成输入光学图像信号的光电转换，生成光电子，输出电子图像；③光电子经过前端近贴聚焦系统入射到MCP上，MCP对电子图像进行倍增；④防离子反馈膜防止高速电子轰击MCP时，产生的离子反向加速对光阴极造成破坏；⑤倍增后的电子图像经荧光屏完成电光转换，输出倍增后的光学图像；⑥光学图像经纤维光锥投射到CCD传感器上，输出数字化微光图像。

2 微光ICCD相机的动态调制传递函数模型

根据已知的微光ICCD相机结构，将动态传递函数模型分解为以下9个部分：动态光学成像系统MTF、光阴极MTF、前近贴电子光学系统MTF、防离子反馈膜MTF、微通道板MTF、后近贴电子光学系统MTF、荧光屏MTF、纤维光锥MTF、CCD传感器MTF。

2.1 动态光学成像系统MTF

理想光学成像系统中，对于一维运动，线扩散函数（LSF）为()。振动引起被照物影响相对光学系统焦平面发生运动，设像点随时间位移公式为()，将位移公式引入线扩散那函数公式后，LSF为[－()]。微光ICCD相机的拍照成像结果为积分时间内能量的叠加，经过对LSF的能量归一化处理，傅里叶变换，求得光学成像系统的动态MTF为[7]：

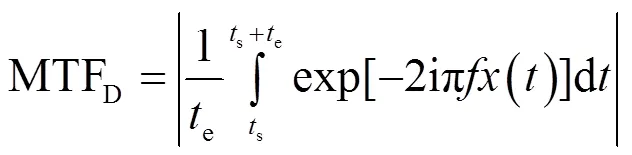
式中：为时间像点位移时间；e为微光ICCD相机积分时间；s为初始积分时间。

2.2 光阴极MTF

光阴极厚度为微米量级，电子在光阴极内传输过程中横向扩散造成的弥散很小，理论极限分辨力可达到1000lp/mm以上，综上，光阴极对三代像增强器MTF的影响可忽略不计[8]。

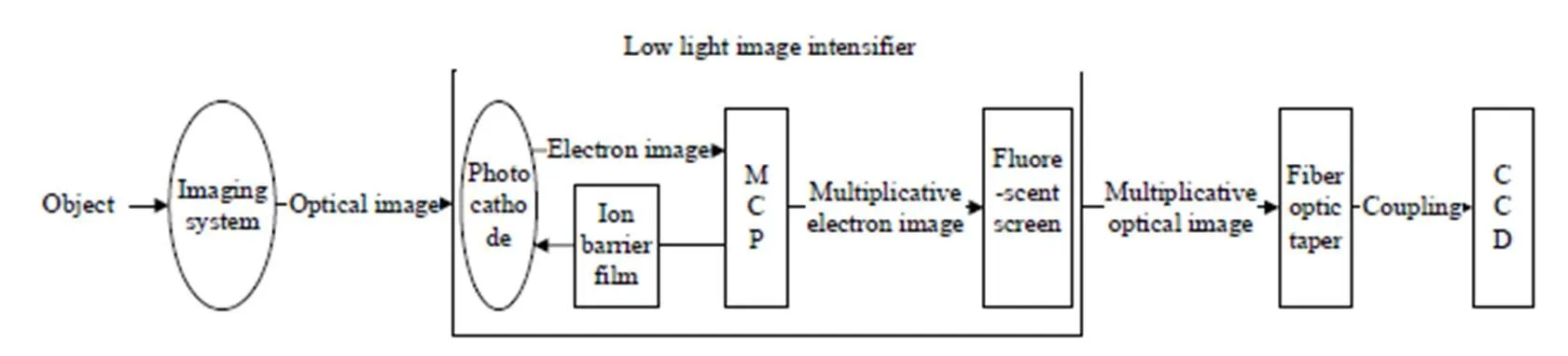
图2 微光ICCD相机工作原理图

2.3 前近贴电子光学系统MTF

三代微光像增强器其光阴极为GaAs光阴极，假设电子出射角度为余弦三次方分布cos3，初始能量分布满足1,8分布，可推导得三代微光像增强器前近贴的MTF为[8]：

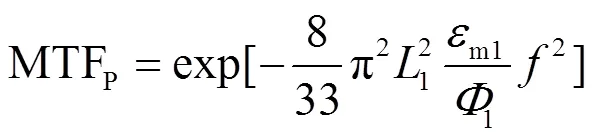
式中：为空间频率，lp/mm；1为前近贴距离，mm；1为加速电压，V；m1为光阴极电子最大初电位。

2.4 防离子反馈膜MTF

防离子反馈膜对成像质量影响很小，若以三代微光像增强器分辨率60lp/mm计算，防离子反馈膜的特征参数(c,c)＝(241, 2)，对应的极限分辨率为450lp/mm，可忽略防离子反馈膜对成像质量的影响[8]。

2.5 微通道板MTF

MCP为三代微光像增强器的电子倍增元器件，其MTF为[8]：

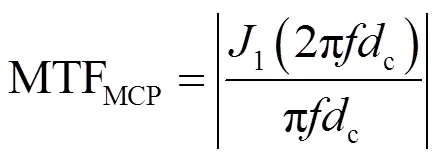
式中：c为MCP单丝直径，mm；1为一阶贝塞尔函数。

2.6 后近贴电子光学系统MTF

假设MCP输出端的电子出射角度为cos3，初始能量分布为2,32分布，推得后近贴电子光学系统的MTF为[8]：

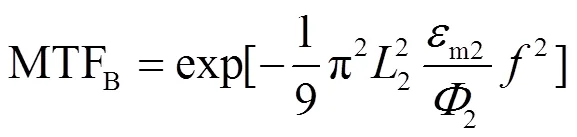
式中：2为后近贴距离，mm；2为后端加速电压，V；m2为最大初电位。

2.7 荧光屏MTF

荧光屏的MTF表示为[8]：

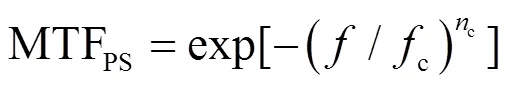
式中：(c,c)为特征参数。

2.8 纤维光锥MTF

纤维光锥MTF为[8]：

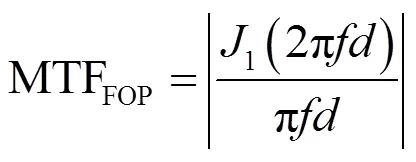
式中：为光学纤维面板单丝直径，mm；1为一阶贝塞尔函数。

2.9 CCD传感器MTF

CCD传感器MTF为[9]：

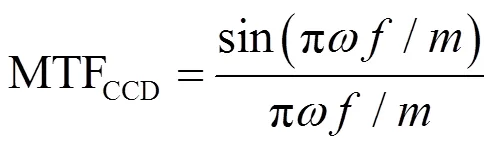
式中：为CCD感光单元尺寸，mm；为CCD传感器的线性放大倍数。

综合上述对ICCD相机动态MTF各部分的分析，本文所研究的微光ICCD相机的动态MTF理论模型见式(8)：

MTFICCD＝MTF×MTFP×MTFMCP×MTFB×MTFPS×MTFFOP×MTFCCD(8)

3 正弦振动下微光ICCD相机动态MTF研究

设定物体成正弦一维振动，则像点位移函数为[7]：

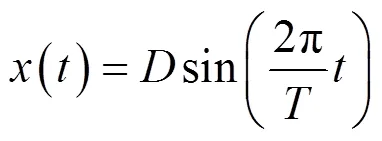
式中：为振幅；为周期；为运动时间。通过相机拍照积分时间与振动周期之比区分低频振动与高频振动，e/＜1为低频正弦振动，e/＞1为高频正弦振动。

3.1 低频正弦振动下的动态MTF研究

当微光ICCD相机积分时间e小于振动周期时，将式(9)代入式(1)可得，低频正弦振动下成像系统的动态MTF如式(10)所示[7]，其中0为0阶贝塞尔函数，2k、2k－1表示不同阶数下的贝塞尔函数，其中为整数，一般取前50阶进行近似计算。将式(10)代入式(8)，可得低频正弦振动下的微光ICCD相机的动态MTF，基于该动态MTF分析积分时间e、振动幅度、振动周期对成像质量的影响。

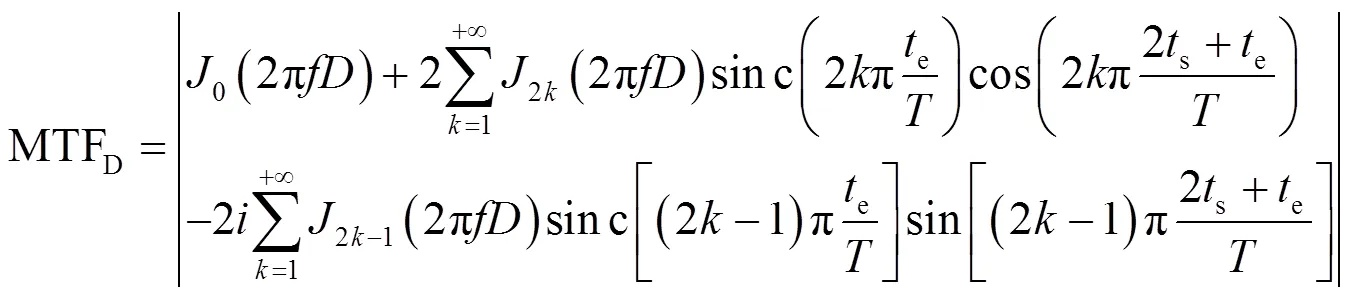
1）振动幅度对成像质量影响分析

①动态光学成像系统MTF参数设定：

初始积分时间s＝0s；

振动周期＝0.1s；

积分时间e＝40ms。

②前近贴电子光学系统MTF参数设定：

前近贴距离1＝0.2mm；

光阴极电子最大初电位m1＝0.5；

加速电压1＝400V。

③微通道板MTF参数设定：

单丝直径c＝6mm。

④后近贴电子光学系统MTF参数设定：

前近贴距离2＝0.5mm；

光阴极电子最大初电位m2＝5；

加速电压2＝5000V。

⑤荧光屏MTF参数设定：

特征参数(c,c)＝(241, 2)。

⑥纤维光锥MTF参数设定：

单丝直径＝5.8mm。

⑦CCD传感器MTF参数设定：

感光单元尺寸＝0.01mm；

线性放大倍数＝0.3。

振动幅度分别取5mm、10mm、15mm、20mm、25mm、30mm，以探究不同振动幅度对成像质量的影响，如图3所示为该参数取值下的动态MTF曲线图。

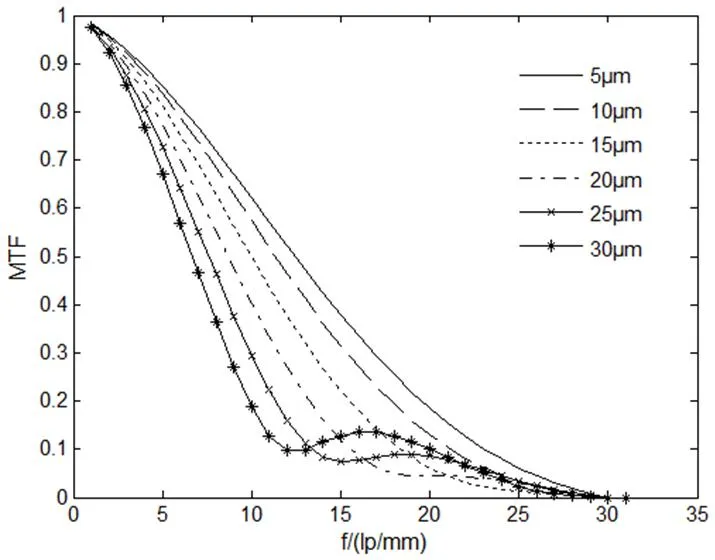
图3 低频正弦振动下不同振动幅度下的MTF曲线

由图3可知，在其他参数不变得情况下，随着振动幅度的增大，动态MTF曲线值随之减小，成像质量随之变差。根据上述分析，为提高微光ICCD相机在振动环境下的成像质量，需采用减振措施，以减小振动幅度。

2）积分时间对成像质量影响分析

参数设定：

＝30mm；e分别取15ms、30ms、45ms、60ms、75ms、90ms以探究不同振动幅度对成像质量的影响；其他参数与上一小节取值相同。如图4所示为该参数取值下的动态MTF曲线图。

图5分析知，在其他参数不变的情况下，随振动周期的增大，动态MTF曲线值呈随机性，成像质量随之同样呈随机性。

3.2 高频正弦振动下的动态MTF研究

当微光ICCD相机积分时间e大于振动周期时，为高频振动。当e为的整数倍即e/=时，为整数，高频正弦振动下成像系统的动态MTF函数为公式(11)所示[7]：

MTF＝|0(2p)|(11)

由上式可知，当e为的整数倍时，成像系统的动态MTF只与振动幅度有关，将式(11)代入式(8)即为微光ICCD相机的动态MTF函数，图6为不同D下的微光ICCD相机动态MTF曲线图。

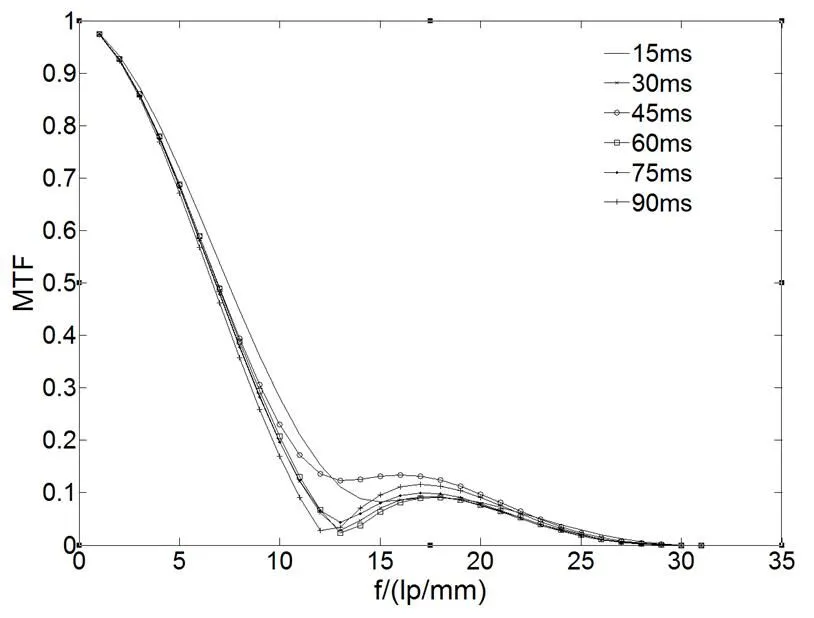
图4 低频正弦振动下不同积分时间下的MTF曲线

图4分析知，在其他参数不变得情况下，动态MTF曲线随积分时间e的增大，变化趋势呈现随机性，不随积分时间增大而增大或减小，积分时间对成像质量的影响呈随机性。

3）振动周期对成像质量影响分析

参数设定：

＝30mm；e＝60ms；分别取0.1s、0.2s、0.3s、0.4s、0.5s、0.6s，以探究不同振动幅度对成像质量的影响；其他参数与上一小节取值相同。如图5所示为该参数取值下的动态MTF曲线图。

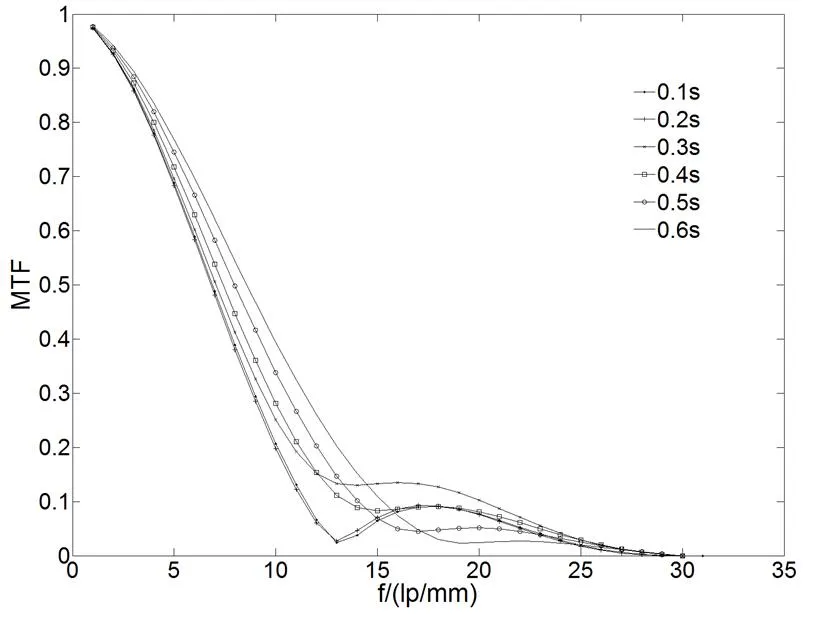
图5 低频正弦振动下不同振动周期下的MTF曲线

由图6可知，当e为的整数倍时，随着振动幅度的增大，微光ICCD相机的动态MTF曲线值随之减小，成像质量随之变差。

当积分时间e大于振动周期，且不为的整数倍时，即e＝Δ＋，高频正弦振动下成像系统的动态MTF函数公式(12)所示[7]：

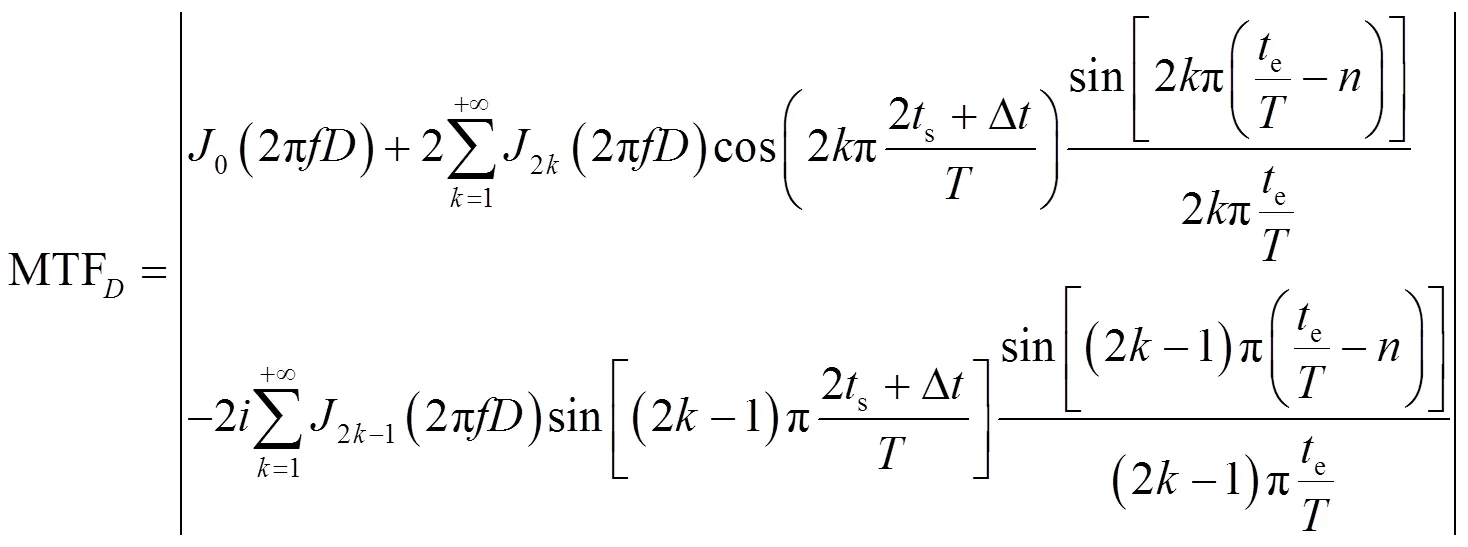
式中：J0为0阶贝塞尔函数；J2k、J2k－1表示不同阶数下的贝塞尔函数，一般取前50阶进行近似计算。将式(12)代入式(8)，可得te＝Δt＋nT时，高频正弦振动下的微光ICCD相机的动态MTF，并分析积分时间te、振动幅度D、振动周期T对成像质量的影响。

1）振动幅度对成像质量影响分析

参数设置：

s＝0；＝0.1s，Δ＝0.05s，＝2，e＝0.25s，振动幅度分别取5mm、10mm、15mm、20mm、25mm、30mm，以探究不同振动幅度对成像质量的影响，其他参数见第3.1小节中的参数设定。如图7所示为该参数取值下的动态MTF曲线图。

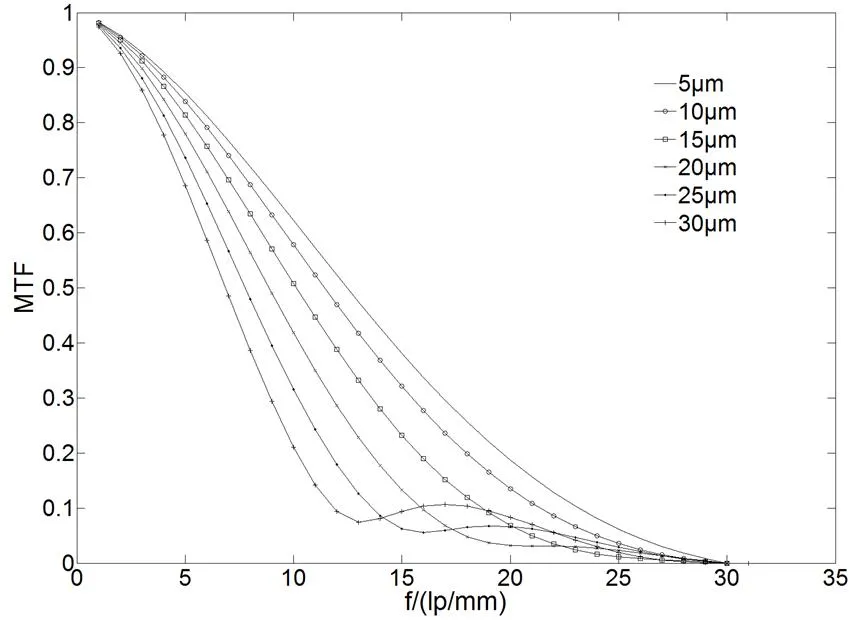
图7 te＝Δt＋nT时高频正弦振动下不同振动幅度下的MTF曲线

由图7可知，在其他参数不变的情况下，随着振动幅度的增大，动态MTF曲线值随之减小，成像质量随之变差。

2）积分时间对成像质量影响分析

参数设置：

＝30mm；＝0.1s；Δ＝0.05s；e分别取Δ＋、Δ＋2、Δ＋3、Δ＋4、Δ＋5、Δ＋6以探究不同振动幅度对成像质量的影响；其他参数与上一小节取值相同。如图8所示为该参数取值下的动态MTF曲线图。

图8分析知，在其他参数不变的情况下，对比低频运动（图4所示），动态MTF曲线值随积分时间e的增大，不再呈现随机性，而随积分时间增加而减小，即成像质量随之变差。

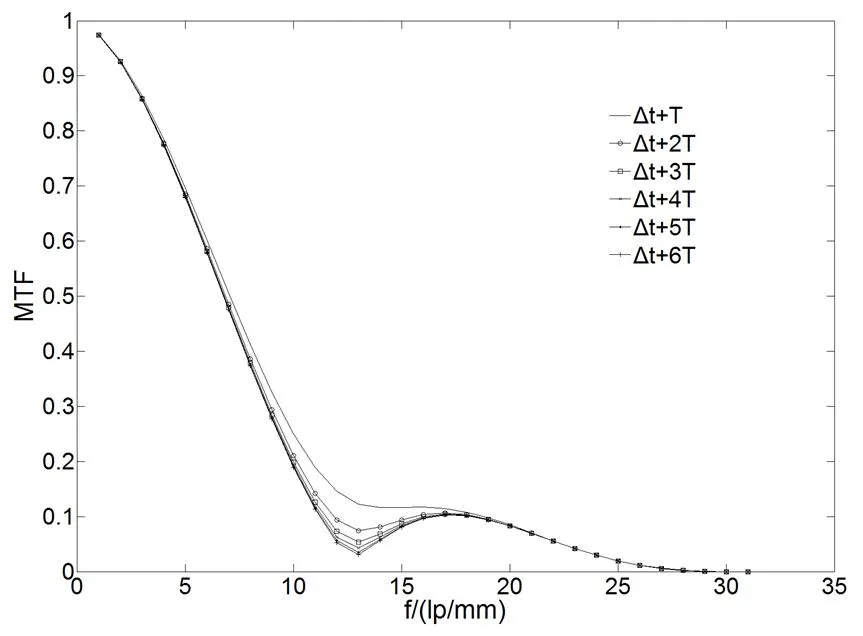
图8 te＝Δt＋nT时高频正弦振动下不同积分时间下的MTF曲线

3）振动周期对成像质量影响分析

高频振动，且积分时间不为振动周期整数倍，因e＝Δ＋，当改变时，e随之改变，故而，无法取单一变量，研究振动周期对动态MTF的影响。在此，高频振动下，振动周期对成像质量的影响不做分析。

4 总结

本文基于微光ICCD相机基本结构，结合理想成像系统的动态MTF及相机各部分的MTF函数，提出了微光ICCD相机的动态MTF理论模型，根据动态MTF，评价微光ICCD相机在振动环境下的成像质量，并研究分析了低频正弦振动及高频正弦振动下的微光ICCD相机在不同振动幅度、振动周期及相机积分时间下成像质量的变化情况。研究指出，在低频及高频正弦振动情况下，随着振动幅度增加，动态MTF曲线值降低，即成像质量变差；在低频振动下，积分时间及振动周期对成像质量的影响呈随机性；在高频振动下，随着积分时间的增加，动态MTF曲线值降低，即成像质量变差；研究振动周期对成像质量影响时，无法取单一积分时间变量，在此，对高频正弦振动下振动周期于成像质量的影响不做分析。综上所述，为提高振动环境下的MTF值，即提高成像质量，需设计减振结构，以减弱振动幅度提高成像质量，根据振动环境参数，设置合适的积分时间，以提高成像质量。

[1] 曾桂林, 周立伟, 张彦云. 微光ICCD电视摄像技术的发展与性能评价[J].光学技术, 2006, 32: 337-343.

ZENG Guilin, ZHOU Liwei, ZHANG Yanyun. Development and performance evaluation of low light ICCD TV camera technology[J]., 2006, 32: 337-343.

[2] 程开富. 微光摄像器件的发展趋势[J]. 电子元器件应用, 2004, 6(10): 7-9.

CHENG Kaifu. Development trend of low light camera device[J]., 2004, 6(10): 7-9.

[3] 麦伟麟. 光学传递函数及其数理基础[M]. 北京: 国防工业出版社, 1979.

MAI Weilin.[M]. Beijing: National Defense Industry Press, 1979.

[4] 王婉婷, 郭劲, 姜振华, 等. 视轴抖动对成像质量影响的研究[J]. 中国激光, 2014, 41(4): 0409001.

WANG Wanting, GUO Jin, JIANG Zhenhua, et al. Study of image quality by los jitter[J]., 2014, 41(4): 0409001.

[5] 王志社. 基于光锥耦合的数字X射线成像系统研究[D]. 太原: 中北大学, 2007.

WANG Zhishe. Research on digital X-ray imaging system based on optical fiber taper coupling[D]. Taiyuan: North University of China, 2007.

[6] 王晓霞. 基于双近贴式像增强器和光锥耦合技术研究[D]. 太原: 中北大学, 2007.

WANG Xiaoxia. Coupling technique research based on two side closer type of image intensifier and the optical fiber taper[D]. Taiyuan: North University of China, 2007.

[7] 杜言鲁, 丁亚林, 许永森, 等. 正弦振动下动态调制传递函数分析与研究[J]. 光学学报, 2015, 35(7): 0711001.

DU Yanlu, DING Yalin, XU Yongsen, et al. Dynamic Modulation Transfer Function Analysis and Research under Sinusoidal Vibration[J]., 2015, 35(7): 0711001.

[8] 陶禹, 金伟其, 石峰, 等. 高性能近贴式像增强器的调制传递函数分析[J]. 光子学报, 2016, 45(6): 0604003.

TAO Yu, JIN Weiqi, SHI Feng, et al. The MTF Analysis of Hight Performance Proximity Image Intensifier[J]., 2016, 45(6): 0604003.

[9] 盛亮, 赵吉祯, 袁媛, 等. ICCD相机动态范围与空间分辨率[J]. 核电子学与探测技术, 2010, 30(4): 500-502.

SHENG Liang, ZHAO Jizhen, YUAN Yuan, et al. Dynamics Range and Spatial Resolution of ICCD Camera[J]., 2010, 30(4): 500-502.

Theoretical Model of Dynamic MTF of Low-Light-Level ICCD

HAN Kun1,2，YAO Ze1,2，QIAO Kai1,2，YANG Shuning1,2，HE Yingping1,2

(1.,71005,;2.,650223,)

During the integration time of the low-light intensified charge-coupled device(ICCD), the spatial vibration causes a decrease in the imaging quality of the low-light ICCD camera. In the case of imaging using low-light ICCD cameras in a vibrating environment, the dynamic modulation transfer function (MTF) is used to evaluate the effect of spatial vibration on imaging quality. Combined with the unique structure of the low-light ICCD camera, the dynamic MTF theoretical model of the low-light ICCD camera is proposed, which can be used to analyze the influence of different factors such as amplitude of vibration, period of vibration and integration time on the imaging quality in low-frequency and high-frequency sinusoidal vibrations.

low-light-level ICCD, dynamic MTF, sinusoidal vibration

TN223

A

1001-8891(2020)05-0294-06

2019-09-24；

2020-02-28.

韩坤（1994-），男，陕西西安人，硕士研究生，主要从事微光像增强器、数字微光器件性能评价技术及微光器件的系统应用研究工作。E-mail：hankunxd@163.com。