钢筋混凝土简支T梁桥加固前后静力特性参数
胡铁明, 刘 通, 李文泉
(1. 沈阳大学 建筑工程学院, 辽宁 沈阳 110044; 2. 辽宁省交通规划设计院有限责任公司, 辽宁 沈阳 110005)
我国许多桥梁在长期使用及外界环境因素影响下,结构损伤不断加重,结构功能不断退化,存在结构老化问题,其表现为不同程度的混凝土开裂、钢筋锈蚀、车道凹折等现象,一定程度上影响行车的舒适性.因此,定期对梁桥存在的病害进行维修养护是必不可少的[1].
曲赜胜等[2]基于抚顺石化公司的加固改造工程实例,详细地介绍了粘贴钢板加固的特点及施工工艺.孙林等[3]以大连胜利桥加固实例,根据梁桥有限元分析的结果,针对该梁桥提出相应的加固方案,并总结该方案的使用范围.长安大学公路学院对板梁桥进行模拟试验[4],首次提出П型钢板粘贴加固,并运用ANSYS仿真程序进行有限元计算,对加固前后T梁进行对比分析.分析结果得出经П型钢板加固后,与普通粘贴钢板相比,可有效地提高T梁底部抗裂性,极限承载能力得到明显地提高.但我国在加铺桥面铺装层方面仍有许多不足,很少采用加厚桥面铺装层加固旧桥.这是由于在加固施工过程中施工工序不严密,加固后的桥面铺装曾在一定程度上出现裂缝、凹槽等现象,导致维修周期越来越短[5].
本文利用MIDAS/Civil进行有限元分析,通过改变钢板和铺装层厚度的特性参数,模拟实际T梁桥的运营情况,对比分析各工况下其加固前后挠度、应力的变化情况,得出各加固参数对T梁极限承载力及抗弯能力的改善程度.
1 研究背景
以辽宁省某高速公路的加固改造工程为依托,根据《公路桥涵设计通用规范》(JTG D60—2015)规定,按公路-Ⅱ级、人群3.5 kN·m-2的载荷标准验算,对该公路进行加固处理.简支T梁桥上部结构采用的混凝土强度等级为C30,跨径组合为12×22.2 m,共设置4道伸缩缝,桥面总宽为8.3 m,横向分布为7.5 m(车行道)+2×0.4 m(防撞栏),全桥布置示意图如图1所示,横断面布置示意图如图2所示.

图1 桥型布置图Fig.1 Bridge layout
该桥存在的病害如下.
1) 全桥多数T梁跨中位置处出现竖向裂缝,部分T梁梁底出现混凝土剥落露筋,最大裂缝长度为3 m,最大裂缝宽度达到0.25 mm以上.
2) T梁接缝处多处存在渗水现象,部分横隔板焊接钢板开裂.
3) 桥面沿纵向均存在宽为0.2 mm以上的裂缝,部分车道存在凹折现象.
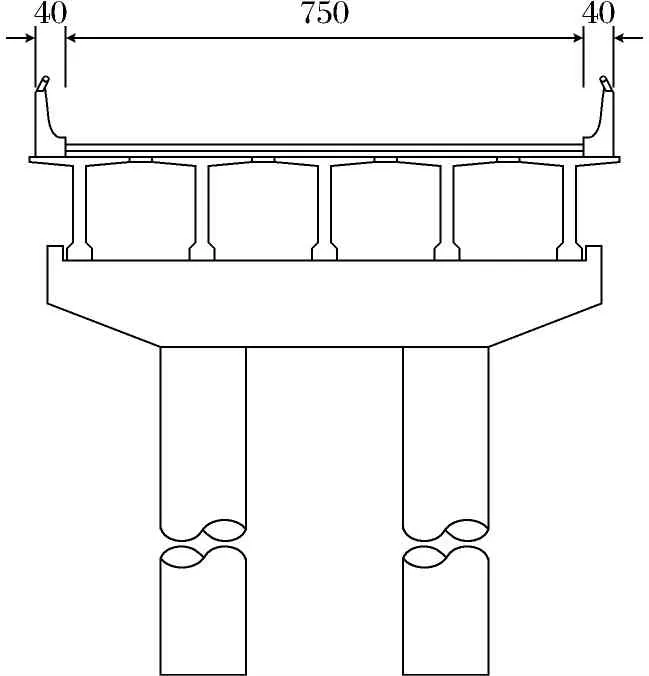
图2 桥梁横断面
Fig.2 Cross section of the bridge
2 有限元模型的建立
简支T梁桥通过横隔板横向连接,将多片T梁形成一个整体来承担外载荷的受力结构.为了对在役梁桥在正常使用状态下进行正确的评价,需要对梁桥整体和局部的受力状态分别进行分析.因此,本文基于有限元分析的基本理论,利用MIDAS/Civil空间分析程序建立全桥上部结构模型进行对比与分析.
此钢筋混凝土简支T梁桥沿横向共有5片梁.几何尺寸如图3所示,材料性能如表1所示.
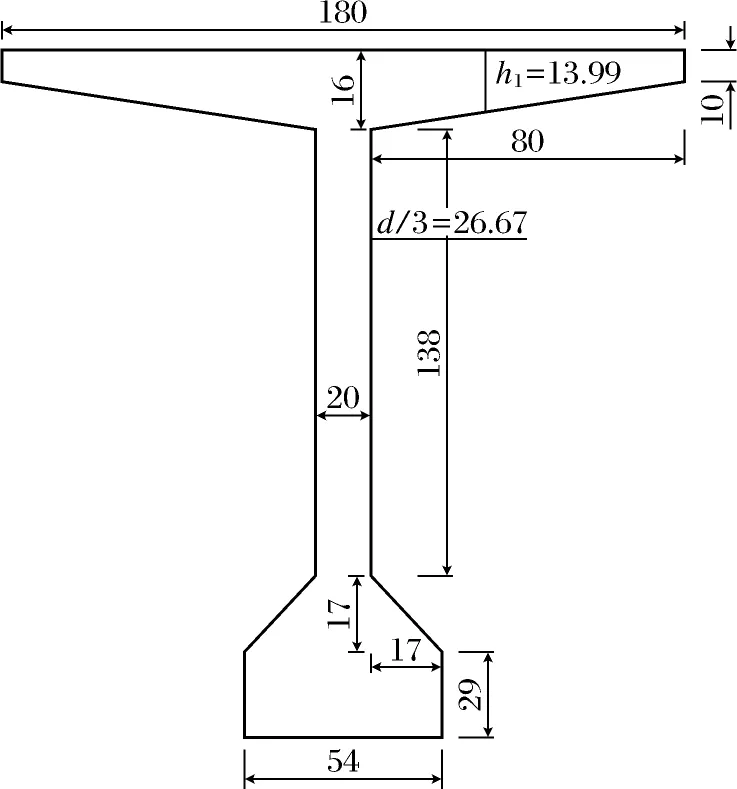
图3 钢筋混凝土T梁桥的几何尺寸
Fig.3 Geometry diagram of reinforced concreteT-beambridge

表1 钢筋混凝土T梁材料性能Table 1 Properties of reinforced concrete T-beam materials
依据《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D60—2004)和《公路桥涵设计通用规范》(JTG D60—2004)取值,梁桥整体温升、温降均按25 ℃考虑,温度梯度按《公路桥涵设计通用规范》(JTG D60—2004)第4.3.10条的规定取值,构件类型按A类构件设计,预制T梁的临时约束用一般支撑模拟.架梁后,成桥阶段的板式橡胶支座用弹性支承模拟,已定义节点的局部坐标系沿x轴平动方向的相关弹性支承刚度为2 436 kN·m-1、沿y轴平动方向的相关弹性支承刚度为2 436 kN·m-1、沿z轴平动方向的相关弹性支承刚度为2.53 GN·m-1;已定义节点的局部坐标系沿x、y、z轴转动方向的相关弹性支承刚度均为0.
3 粘贴钢板法与加固前T梁桥承载能力对比
3.1 粘贴钢板法对T梁挠度的影响分析
梁底粘贴的钢板长度均为18 cm,T梁加固方式如表2所示,建立5个模型.采用分级加载的方式,对各加载工况下钢筋混凝土T梁施加集中力P,直至混凝土应力达到《混凝土结构设计规范》(GB 50010—2010)中C30混凝土强度设计值fc=14.3 MPa时停止加载.

表2 T梁加固方式Table 2 T-beam reinforcement methods
借鉴钢梁叠合梁模型中混凝土与钢梁的连接方式,以弹性连接中钢梁的刚性与混凝土单元连接和粘贴钢板中的锚栓类和剪力钉的建立方法,以图3为依据,建立如图4所示的单梁有限元模型.
根据5组有限元模型提出的数据(见表3)绘出载荷-挠度曲线,以此观察相同载荷作用下T梁的挠度变化,变化规律见图5.

(a) T梁粘贴钢板的有限元模型(b) T梁在载荷作用下的变形
图4 单梁有限元模型
Fig.4 Single beam finite element model

表3 加固后不同载荷下T梁的挠度Table 3 Deflection value of the T-beam after reinforcement under different loading conditions mm

图5 载荷-挠度曲线Fig.5 Load-deflection curve
由图5得知,在相同载荷作用下,钢板的挠度随着钢板厚度的增加而降低,且降低的趋势较为明显.原因分析如下:梁底钢板通过锚栓与T梁连接使梁体的刚度增加,在作用相同的载荷下T梁的位移有所减小,限制了梁底的变形.
为进一步分析不同厚度的钢板对梁体挠度的影响,计算了不同加载工况下梁底挠度降低的百分比,如表4所示.由表4可知,T梁挠度降低的百分比与梁底粘贴不同厚度的钢板之间呈线性关系,在同一载荷作用下,T梁挠度随着粘贴钢板厚度增加而减小,但降幅也逐渐减小.
为检验所得的单梁结论可以运用到实际的桥梁加固模型中,利用梁格法建立本文依托工程中的钢筋混凝土简支T梁桥模型分析,验证关于粘贴钢板的结论的准确性,有限元模型如图6所示.
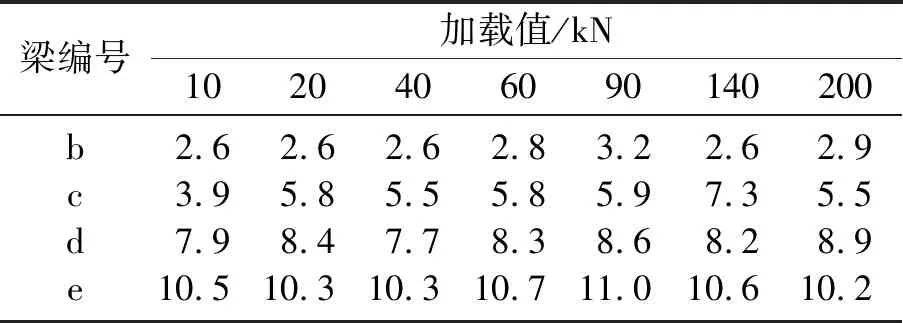
表4 加固后不同载荷下T梁挠度降低的百分比Table 4 Percentage of deflection of T-beam after reinforcement under different loading conditions %
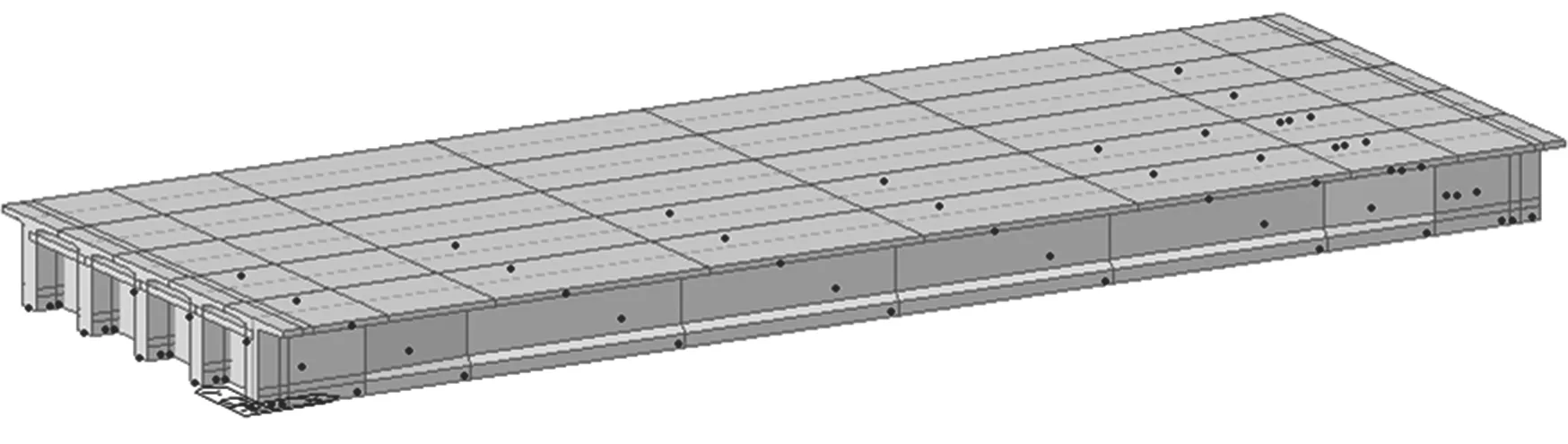
图6 梁格法建立全桥上部结构计算模型Fig.6 Calculation model of the whole bridge’s upperstructure by beam-grid method
采用表2的几种加固方式建立5组加固模型,分析公路-Ⅱ级的中载工况下各加固方式T梁的竖向挠度变化情况,并绘制挠度对比图来直观分析粘贴钢板对T梁的影响.各片T梁竖向挠度对比曲线如图7所示.
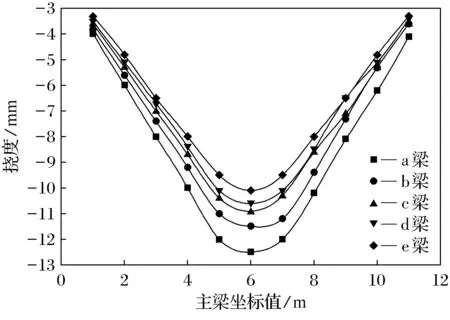
图7 活载作用下各片T梁竖向挠度变化规律Fig. 7 Vertical deflection of the T-beam under live load
通过图7可以得出与未加固a梁相比,b梁加厚2 mm钢板挠度降低了2.9%;c梁加厚3 mm钢板挠度降低了5.6%;d梁加厚5 mm钢板挠度降低了8.3%;e梁加厚7 mm钢板挠度降低了10.3%.挠度降低量与上文单梁模型的挠度降低量基本相同,符合上文单梁模型的结论.
3.2 粘贴钢板法对T梁应力的影响
从图6加固的有限元模型中提取相应跨中界面上缘与下缘的应力值,具体数据如图8、表5所示.
由图8、表5可知:粘贴钢板法加固后的各片T梁的上缘与下缘应力均有不同程度的降低,且下缘应力降低的幅度较大;T梁应力降低的幅度随着钢板厚度增加而增大,且下缘应力降低的幅度比上缘应力降低的幅度大,主要原因是由于梁底钢板与被加固混凝土的可靠粘结,二者共同承担车道载荷,梁底混凝土应力减小的一部分由钢板承担,使其结构的承载能力和强度得到明显的改善.

图8 跨中截面上缘与下缘应力对比Fig.8 Comparison of the upper and lower edgestresses of the midǒsection
表5 车道载荷作用下加固前后的各片T梁的跨中应力降低百分比 Table 5 Percentage reduction in mid-span stress of each T-beam before and afterreinforcement under lane load %

梁编号应力降低百分比上缘下缘b1.44.3c3.18.4d4.511.5e6.014.3
3.3 粘贴钢板法对T梁桥模态的影响
为更好地了解该梁桥本身结构的动力性能,对其粘贴钢板模型中的动力特性参数,即固有频率进行对比分析.提取各梁有限元模型中的前9阶固有频率,频率-阶数数据及对比情况见表6.
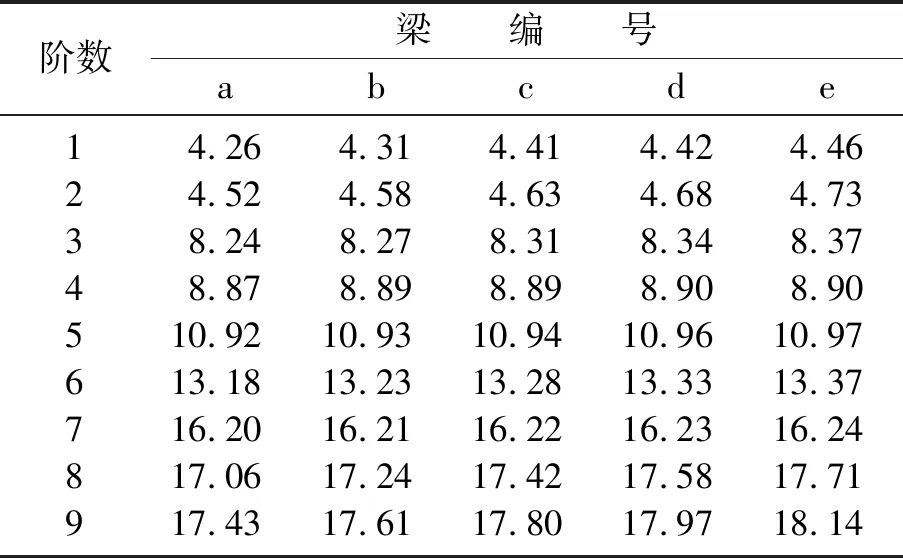
表6 有限元分析前各阶固有频率Table 6 Natural frequency of each order beforefinite element analysis Hz
由表6数据经计算可得:粘贴2 mm厚度的钢板较原梁(a梁)第9阶基频可提高1.03%,粘贴3 mm厚度的钢板较原梁基频可提高2.12%,粘贴5 mm厚度的钢板较原梁基频可提高3.10%,粘贴7 mm厚度的钢板较原梁基频可提高4.1%.采用粘贴钢板法加固后基频有提升,但是幅度不大.
4 加铺桥面铺装层法与加固前T梁桥承载能力对比
4.1 加铺桥面铺装层法对T梁的挠度影响
加厚桥面铺装层加固通常是先将桥面进行打磨处理,之后重新浇注钢筋混凝土铺装层,利用梁体截面的加高,增加桥梁的抗弯能力,同时改善桥梁横向传递载荷的能力,从而提高桥梁的承载能力.桥面铺装是受力复杂的动力体系,一方面传递分配载荷并参与桥面板的受力,另一方面联结各T梁共同受力[6-7],加固设计中铺装层厚度对桥梁结构影响较为明显.
以图3的结构尺寸分别建立了铺装层厚度为2、3、5和7 cm的有限元模型,在建模分析中,考虑铺装层与桥面板之间材料性能及两者之间粘结层应力的影响,加厚桥面铺装层选取的材料应等于原桥T梁的材料强度等级,这就意味桥面铺装层与下面的板、边梁和T梁形成整体,共同受力,而采取的方式可以通过增大原桥T梁顶板的截面高度进行模拟[8].
由于顶板受压区的加固会使T梁恒载的自重增加,而恒载的增加影响结构的受力,同时板顶经加固后由于截面面积增大,中性轴上移,其截面刚度有所提升,因此要考虑加厚桥面对T梁所产生的影响.
自重和活载工况下加铺不同厚度铺装层的挠度见图9,加铺不同厚度铺装层的恒载弯矩见图10.由图9、图10可知,自重和活载2种工况下加铺不同铺装层厚度的挠度值及恒载弯矩值随着顶板受压区截面高度不断增加,结构自重也得到相应增加,恒载弯矩也逐渐变大,但这种情况对结构的受力是不利的.2种工况下跨中截面的挠度值随着铺装层厚度的增加均呈现不同程度的下降.铺装层厚度增至3 cm时,自重作用下挠度值由12.60 mm降至12.05 mm,降幅为4.4%;而在公路-Ⅱ级的车道载荷作用下,挠度值由10.64 mm降至9.14 mm,降幅为14.1%;当铺装层厚度由3.00 cm增至7.00 cm时,自重作用下挠度值由12.15 mm降至11.92 mm,降幅为1.9%;公路-Ⅱ级的车道载荷作用下挠度值由9.14 mm降至8.96 mm,降幅为2.0%.说明在自重作用下,铺装层增加的太多对刚度的增加并不明显,反而增加结构自重,降低其承载能力.而公路-Ⅱ级下,加厚桥面铺装层对T梁的承载能力提升表现明显,且桥面厚度的增加在一定程度上随厚度的提升承载能力也逐渐增大.经对比发现,加铺铺装层的最佳厚度为3~5 cm.
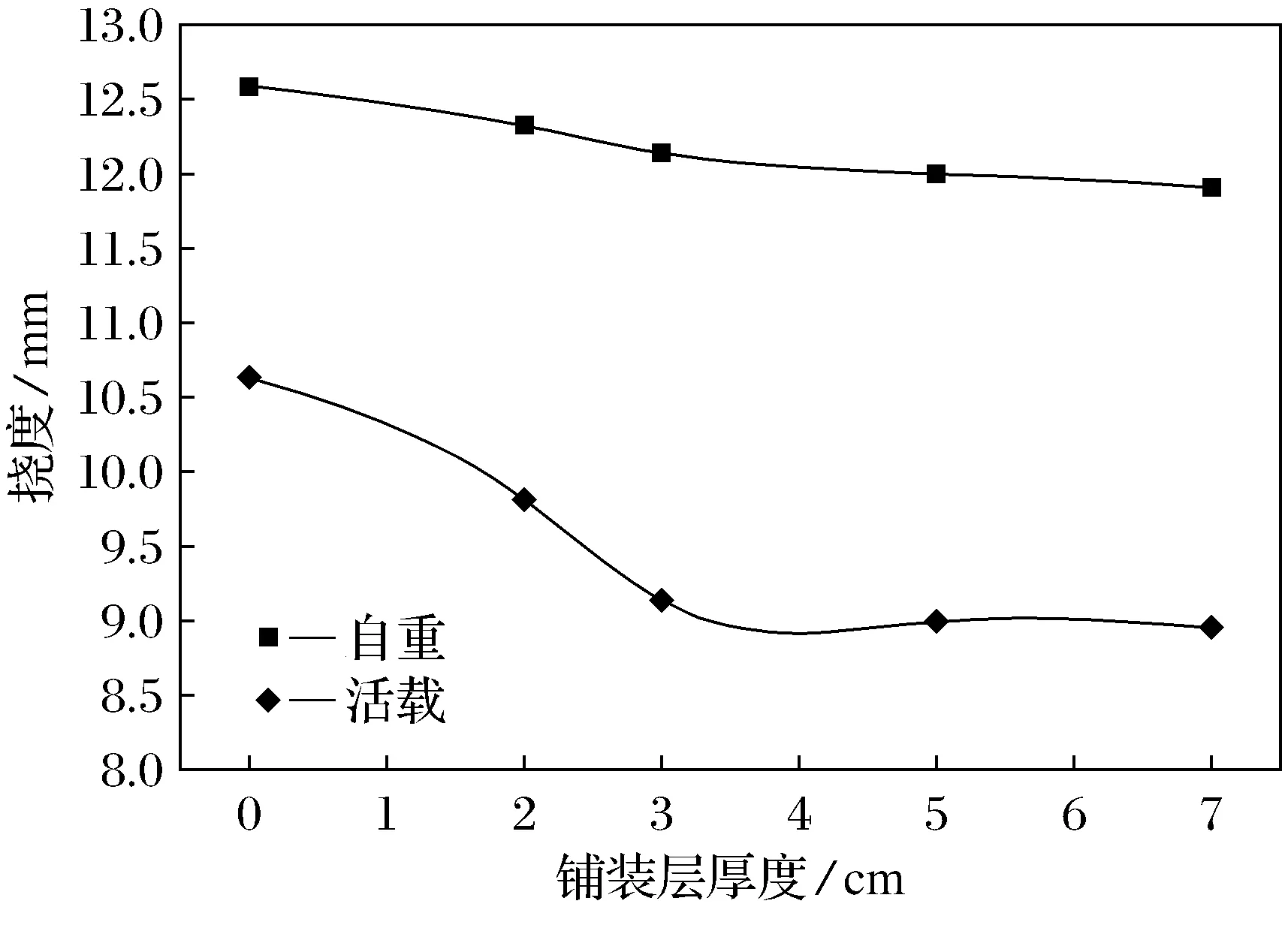
图9 自重和活载工况下加铺不同厚度 铺装层的挠度对比Fig.9 Comparison of deflection of paving layers withdifferent thickness under self-weight and live load
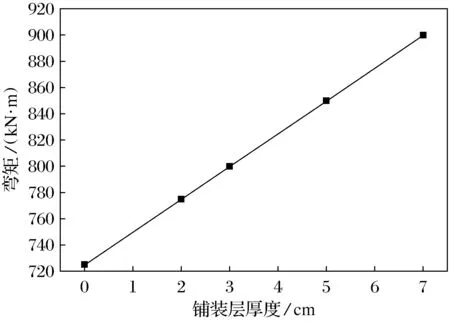
图10 加铺不同厚度铺装层的恒载弯矩Fig.10 Constant-load bending moment of thepaving layer of different thicknesses
4.2 加铺桥面铺装层法对T梁的应变影响分析
利用MIDAS/Civil软件的截面联合功能,建立增加铺装层厚度的模型,如图11所示.中载活载作用下不同厚度铺装层下缘应变情况见图12,由图12可知,梁底应变随着铺装层厚度的增加而减小,增加2 cm厚度的铺装层,跨中应变减少0.9%;增加3 cm厚度的铺装层,跨中应变减少2.7%;增加5 cm厚度的铺装层,跨中应变减少5.3%;增加7 cm厚度的铺装层,跨中应变减少12.0%;之后梁体下缘的最大应变虽然有所减小,但逐渐趋于平缓,说明铺装层继续增加对桥梁的横向联结性能影响不大,反而增加桥梁自重,降低桥梁的承载能力,由此可验证增加铺装层厚度可提升T梁的承载能力.

图11 加铺桥面板铺装层厚度的有限元模型Fig.11 Finite element model of the thickness of the pavement of the bridge deck

图12 中载活载作用下不同厚度铺装层 下缘应变对比Fig.12 Comparison of the lower edge strain of thepavement layer with different thicknesses under the action of the medium-load live load
5 组合加固法与加固前T梁桥承载力对比
5.1 组合加固法对T梁的正截面抗弯承载能力影响
将粘贴钢板和加铺桥面铺装层2种加固方法组合之后的有限元模型与未加固桥的模型进行对比分析,组合加固后的有限元模型如图13所示,采取的加固方案如表7所示.

图13 组合加固有限元模型Fig.13 Finite element model of combined reinforcement
表7 拟采用的加固方案
Table 7 Proposed reinforcement schemes

编号方 案Ⅰ加5cm铺装层+粘贴2mm厚钢板Ⅱ加5cm铺装层+粘贴3mm厚钢板Ⅲ加5cm铺装层+粘贴5mm厚钢板Ⅳ加5cm铺装层+粘贴7mm厚钢板
以《公路桥涵结构设计通用规范》(JTG-D62—2004)中的公路-Ⅱ级为设计参数,在正常使用状态下各T梁需满足的抗弯承载力如表8所示.
由表8可知,各片T梁在公路-Ⅱ级的设计条件下,其正截面抗弯强度需大于2 370.04 kN·m时方能达到使用要求.
未加固与组合加固法加固后的T梁正截面抗弯承载力的对比情况见图14,采用4种组合加固方法加固后梁的正截面极限弯矩分别为2 841.74、2 931.65、3 095.41、3 116.35 kN·m,而仅釆用增加铺装层厚度加固方法加固后T梁正截面极限弯矩为2 445.60 kN·m,与未加固T梁相比,增加铺装层厚度后的正截面抗弯承载能力提升了10.43%,采用方案Ⅰ提高了22.92%,采用方案Ⅱ提高了33.83%,采用方案Ⅲ提高了41.30%,采用方案Ⅳ提高了42.28%.经对比分析可知,组合加固法对结构的抗弯承载力提升效果明显,结合加固效果分析,选择方案Ⅲ,即采用加厚5 cm铺装层及粘贴7 mm厚钢板能够最大程度地提升原桥承载能力.

表8 各片T梁在正常使用状态下抗弯承载力的极限值Table 8 Limit value of flexural capacity of each T-beam under normal use
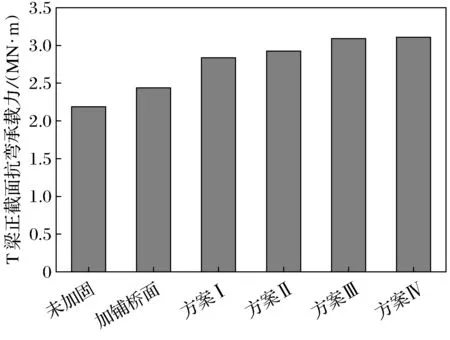
图14 不同加固状态下T梁抗弯承载力对比Fig.14 Comparison of flexural bearing capacity of T- beams under different strengthening conditions
5.2 组合加固法模型对T梁的刚度影响
从上文分析可知,在各自相应的工况下,梁底粘贴钢板加固和加厚桥面铺装层均能不同程度地降低T梁的挠度,为了对比不同加固方案下沿梁桥纵向挠度的连续变化情况,采用方案Ⅲ、Ⅳ,从有限元模型中沿顺桥方向在梁底选取7个节点,绘制中载工况下a梁和c梁的竖向挠度.
在方案Ⅲ、Ⅳ与未加固情况下不同位置处a梁和c梁竖向挠度的对比图如图15、图16所示.由图15、图16可知,采用组合法加固的模型,挠度比未加固梁最多降低37.8%,选取a梁、c梁挠度平均各下降31.6%和34.2%.
采用粘贴钢板法加固法中,粘贴5和7 mm厚度的钢板,T梁的挠度分别降低了8.2%和11.0%.采用加铺桥面铺装层法加固,加厚7 cm的桥面,T梁的挠度可降低28.9%.而组合法加固,在中载工况下,a梁和c梁的挠度降低39.3%和37.8%,基本相当于2种单独加固效应叠加起来.根据以上分析结果可得出,采取组合法加固方式可以有效地提升T梁桥的刚度.

图15 不同位置处a梁竖向挠度对比Fig.15 Comparison of vertical deflectionof a-beam at different locations

图16 不同位置处c梁竖向挠度对比Fig.16 Comparison of vertical deflectionof c-beam at different locations
5.3 组合加固法模型对T梁的应变对比
为研究T梁桥在公路-Ⅱ级级车道载荷作用下组合法加固对T梁强度的影响,采用表7中的加固方案Ⅲ、Ⅳ与原桥的应变值进行对比,沿梁高应变测点布置如图17所示.各片T梁的应变对比如图18、图19所示.

图17 应变测点布置Fig.17 Strain measurement point layout
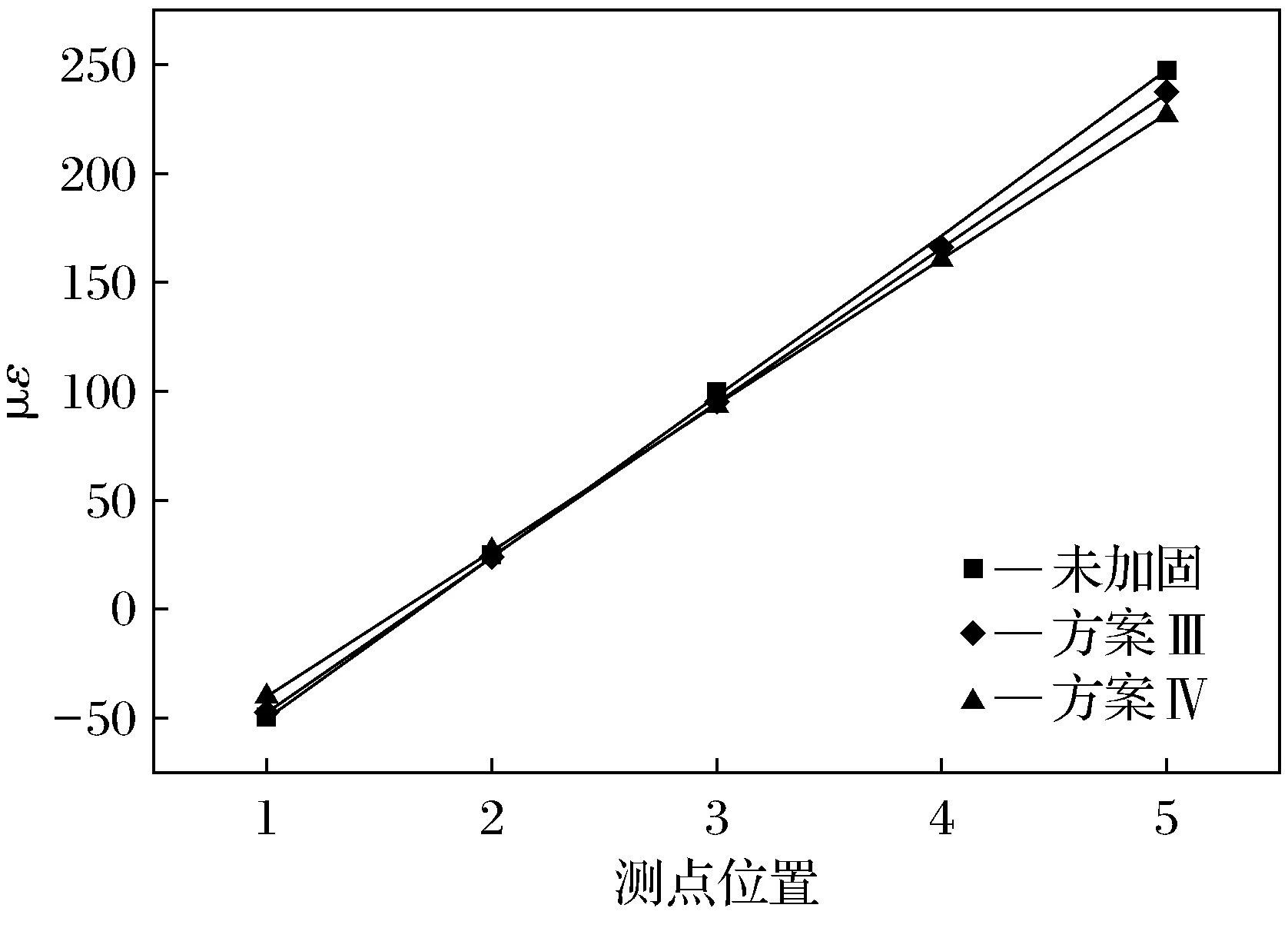
图18 中载状况下a梁应变对比Fig.18 Comparison of strain of a-beam under medium load
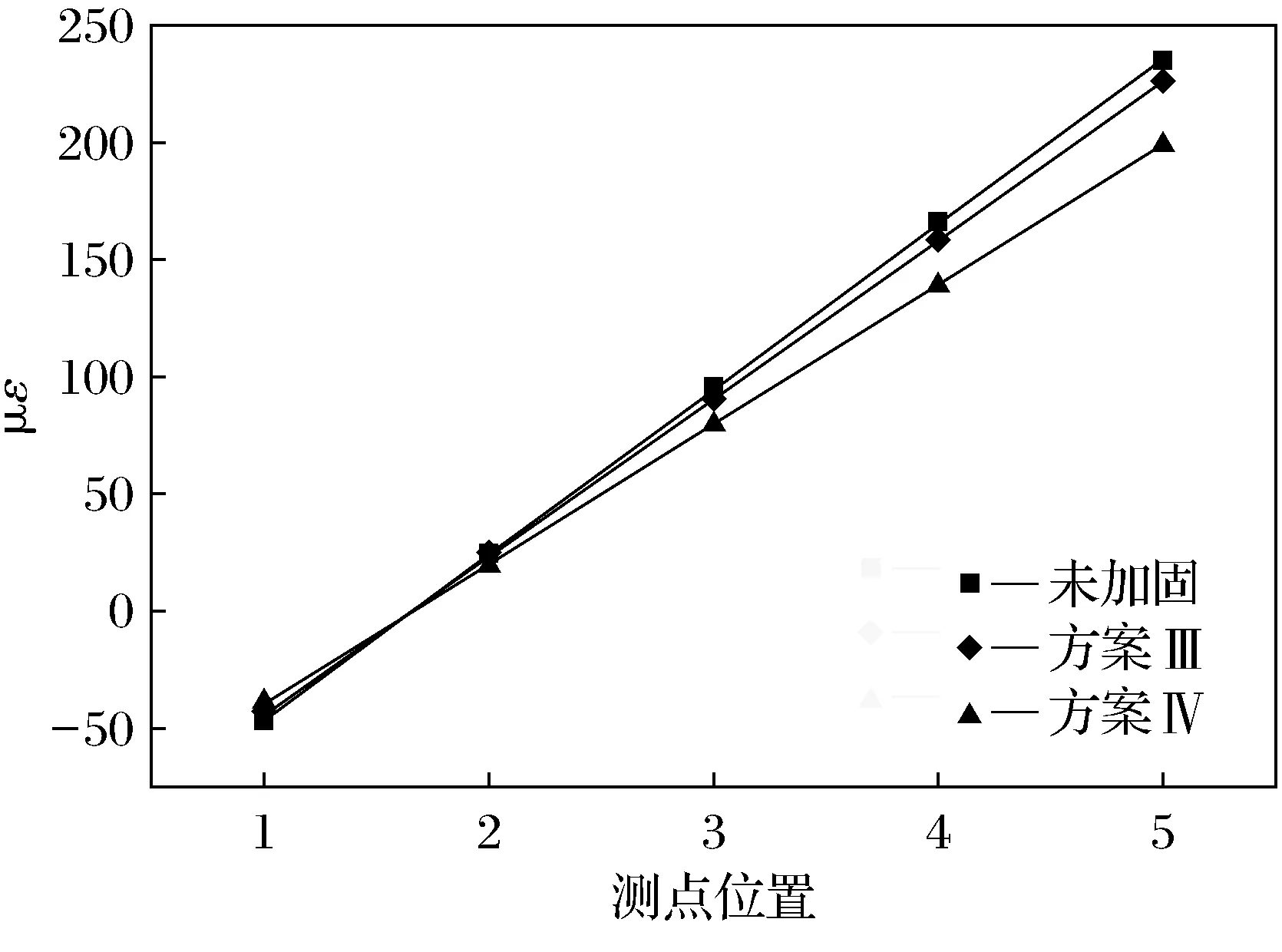
图19 中载状况下c梁应变对比Fig.19 Comparison of strain of c-beam under medium load
由图18、图19可知 ,采取组合法加固的模型,在中载工况下,a梁沿梁高的5个测点应变值平均减少了11.7%,梁底应变值减少了14.3%;c梁沿梁高的5个测点应变值平均减少了19.6%,梁底应变值减少了21.5%.
由表5、图12分析可知,在粘贴钢板加固和桥面铺装层加固效果分析中,采用粘贴钢板法加固,即粘贴5和7 mm厚的钢板上缘应变分别减少4.5%和6.0%,下缘应变分别减少11.5%和14.3%.采用桥面铺装层加固的T梁跨中应变可以减少12.0%.而组合法加固比粘贴钢板加固和桥面铺装层加固的应变减少百分比为14.3%~23.7%,相当于2种单独的加固方式效应叠加起来.因此采取组合法加固可以有效地提升T梁桥的截面强度.
6 结 论
1) 采用粘贴钢板法加固T梁桥时,不同厚度的钢板使T梁在相应工况下挠度降低的百分比基本呈线性.随着钢板厚度不断增加,T梁挠度逐渐降低,但降低的幅度也逐渐减小.梁体下缘混凝土应力降低的幅度比上缘应力降低的幅度大,说明钢板可以分担梁体一部分的应力;粘贴钢板法对基频的提升影响较小.
2) 采用桥面铺装层法加固T梁桥时,其加固对原桥的刚度提升较为明显.各工况下T梁挠度均有所降低,而公路-Ⅱ级作用下挠度降低量较大,约为16%.
3) 综合经济因素和加固效果采用组合加固法,对本文中的T梁桥加铺5 cm铺装层,并在梁底粘贴7 mm钢板,其正截面承载力与原桥相比提高了42%,在挠度和应力方面的影响基本相当于2种单独加固方式效应叠加起来.

