基于工况TPA的舰船辐射噪声预报与试验研究

马中存，张永祥

(1.中国人民解放军91202部队，辽宁 葫芦岛 125000；2.海军工程大学 动力工程学院，湖北 武汉 430000)

0 引言

舰船本身是一个十分复杂的噪声源，主要分为机械噪声、水动力噪声以及螺旋桨噪声[1]。通常舰船在中低速航行下机械噪声占主要成分，对舰船的辐射噪声贡献最大。机械噪声主要是由舰船上的机械设备(发动机、空压机、空调和各种泵等)运转而产生的噪声[2-3]，这些设备在工作过程中产生振动，通过设备基座或者内部的支架传递到舰船壳体，从而引起舰船壳体振动并向海洋中辐射声波[3]。舰船机械噪声控制往往从两个方面来进行，即振源控制和传递路径控制。由于舰船机械设备众多，机械噪声源数目多且复杂，源与源之间耦合严重，振动噪声源的传递路径极其复杂，其前提便是进行舰船振动噪声的传递路径分析方法研究。一方面可以识别舰船机械噪声的主要振动噪声源以及传递路径，指导舰船减振降噪措施的合理实施；另一方面可以完成舰船的辐射噪声预报以及设备故障诊断，提高舰船声学性能[4-5]。

传递路径分析方法(Transfer Path Analysis, TPA)是近些年快速发展的一种基于试验的振动系统中能量传递路径的研究与控制方法[6-7]，其雏形自1993年被Van der Linden P J G等提出，应用在汽车的结构传递噪声诊断。该方法历经了20余年的研究和发展，广泛应用汽车NVH、船舶、航天等领域，核心就是研究系统传递特性，解决任何振动噪声源—传递路径—响应点的问题[8-10]。针对舰船设备众多、源与源之间耦合严重等特点，本文结合偏相干分析方法，采用工况TPA方法[11]，通过对舰船振动噪声的传递特性分析，确定一个多输入输出系统中主要的振动噪声源以及传递路径，实现振动噪声的合成，为舰船的噪声控制、故障诊断以及噪声预报提供理论指导，并通过消声水池的舱段模型试验进行验证。

1 传递路径理论分析

1.1 工况TPA分析

工况TPA方法按照各子路径响应来表现目标点处的响应。当舰船系统受到外在或内在激励时必然会产生响应，而在此表征这种激励与系统响应之间的关系便为系统的传递函数。由于舰船振动系统会受到多种振动噪声源同时激励，每种激励都会通过不同的传递路径传递到多个目标响应点。工况TPA方法应用不同工况下所得的振源信号，从而建立目标响应点与每个振源间的传递关系[7]，利用舰船正常运行时的振动信号便能合成舰船内或者船体外目标点的声场信号。

设舰船系统内某一目标点处的声压信号为p(w)，振源振动加速度信号为xj(w)，其通过舰船的振动衰减系统Tj(w)可得：

(1)

式中：m为振源的个数。

设舰船船体结构系统船体函数Tj(w)为线性，工况载荷为任意r个，目标点的声压信号为pk(w)(k=1,2,…,r)与振源处的加速度信号xkj(w)通过计算产生r个线性方程组为：

pk=xk1T1+xk2T2+…+xkjTi+…+xkmTm

(2)

式(2)还可以表示成矩阵形式为：

P=XT

(3)

式中：P为输出声压矩阵；X为输入振源；T为系统传递函数。

矩阵各种输入工况被看作输入矩阵X的各个行向量，不同的振源输入被看作该行向量的各个元素。适当选取工况及工况类型的组合是准确获得舰船振动系统传递函数矩阵T的前提。在选取工况时，遵循r≥m的原则，其所选工况相互之间不相干。当各个输入工况仅仅为幅值或者相位的变化时，其不利于传递函数T的准确求取，而是需要施加不同结构载荷如发动机或者其他设备等在不同转速、不同负载下的工况[7,10]。所以，在进行试验时，各种输入工况的参考信号的测量传感器应该尽可能地放置在激励源附近，以求最大限度的来获取互不相干的激励信号。另外，当载荷工况的组合导致矩阵X各行向量存在较强的相关性或者加性噪声包含在所测的振动加速信号矩阵X和声压信号矩阵P时，传递函数矩阵T的准确性则会受到较大的影响，此时应用偏相干函数法可以有效地解决此类问题[5,12]。

1.2 偏相干分析

简单来说，在舰船振动传递路径分析系统中，假设用一组有序的时域信号x1(t)，x2·1(t)，…，xn·(n-1)!(t) 表示偏相干分析方法得到的条件输入，以此来表示已知的原始输入。则xi·(i-1)!(w)，i=1,2,…，n，N(w)、Y(w) 分别表示有序条件输入下的输入信号的傅里叶变换、系统噪声的傅里叶变换和输出信号的傅里叶变换，Lxiy(w)表示有序条件输入下的一组最优的系统传递函数[13]，下标i·(i-1)!表示的是应用最小二乘法原理去掉前(i-1)个输入信号的线性影响之后的第i个条件输入。此时系统输出可表示为：

(4)

输入信号xi(t)与输出响应信号y(t)之间的偏相干函数被定义为它们的条件谱密度的常相干函数。则偏相干函数为：

(5)

在各个输入信号之间存在相干的情况下，则系统输出自功率谱密度函数表示为：

(6)

在式(6)中：公式左端Gyy(w)表示系统输出自功率谱密度函数；公式右端第一项代表x1(t)对y(t)的相干输出功率谱，第二项代表在去掉x1(t)对y(t)的影响下，x2(t)对y(t)的偏相干输出功率谱[13]；下面的以此类推。

通过以上的分析，应用偏相干以及条件功率谱分析可以解决输入信号之间耦合的问题，并且不改变原始输入信号与输出信号之间固有的相干性，从而优化工况TPA模型，提高传递函数矩阵T的准确度，解决耦合振动噪声源之间的舰船振动传递路径分析问题[14]。

2 舱段模型试验分析

2.1 试验系统

以缩比的舱段模型为试验对象，模型长3.5 m，外直径为2.5 m。在舱段内底部安装1套浮筏隔振装置，两端各安装1台振动电机，通过隔振器与隔振装置相连。在舱段中间，激振器通过减振器安装在舱段内水平横梁的基座上，减振器可以通过螺杆来选择刚性连接或弹性软连接。激振器的激励力为500 N，频率可调，最高激振频率为5 000 Hz。

试验系统主要由两部分组成：振动发射系统和振动测量系统。同时，避免在反映同一振动信息的位置布置多个加速度振动传感器，以便减少信号之间的耦合，提高试验的精度。加速度传感器布置见图1。在设备机脚、舱壁内测及外侧共计布置30个加速度传感器，分别表示为p1～p30； 1#与2#水听器布置在激振器一侧，与舱段模型中轴线深度等同，距舱段模型正横方向9 m和11 m处。

图1 传感器布置示意图

试验过程中，设计设备单机运行以及设备组合运行，具体见表1。分别进行岸上及水下测试，水下模型吊放深度(中心轴距离水平面)5 m。试验采样频率为20 kHz，采样长度70 s，数据以tdms格式保存在计算机中。

表1 工况设计表

2.2 辐射噪声合成与实测值对比分析

试验中，选择工况5激振器与振动电机A同时开启，激振器发射从20 Hz到2 000 Hz的1/3倍频程(1/3 oct)信号，分别在不同幅值和频率的激励下，分析舱段模型中设备经减振器到舱壁，舱壁到外部1#、2#目标点水听器的传递特性。利用已建立的工况TPA模型，对目标点噪声进行合成，试验假设传递函数不随激振器输入激励信号的激励幅值与激励的先后顺序的变化而变化，认为该舱段模型满足系统的线性不变性。

比较图2可以看出，除50、25、20 Hz等个别频点受系统及设备耦合作用较强外，1#与2#测点噪声合成值与实测值相差较大，其余频点处的噪声合成值与实测值基本吻合，相差在2 dB以下。试验中：一方面振动电机产生以49.96 Hz为中心频率的窄带信号，伴随50 Hz的工频电干扰，两者都会影响噪声合成；另一方面，激振器发射低频信号激励壳体时，壳体发生谐振也会影响噪声合成。因此，通过单独开启激振器，结合偏相干分析，先进行解耦再进行舰船振动传递特性分析，见图3。

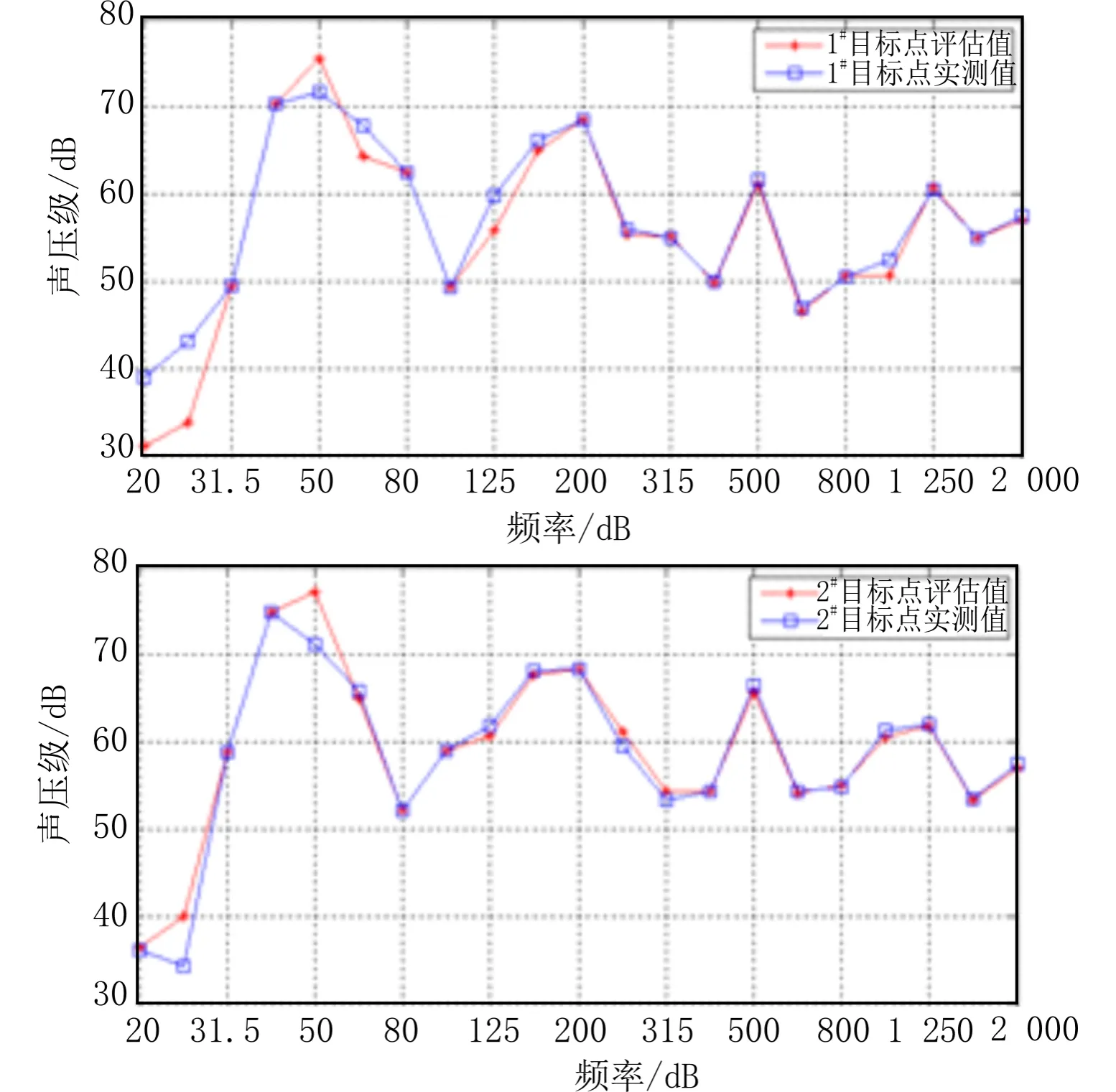
图2 1#、2#测点辐射噪声各个频率处合成与实测值

图3 偏相干优化后1#、2#测点辐射噪声各个频率处合成与实测值

由图3可以看出，经偏相干优化后，1#目标点50 Hz处振动噪声合成值与实测值相差小于2 dB，2#目标点振动噪声合成值与实测值相差小于1.8 dB，其他低频处噪声合成精度也有所提高，都小于3 dB。优化后的目标点噪声合成值与实测值吻合较好，满足水下振动噪声分析的基本要求。以1#目标点为例，优化前和优化后振源对目标点贡献量的分析见图4。从图中发现，振动电机较激振器的能量传递衰减量要大，贡献比小于激振器；而经偏相干分析优化后，振动电机对1#目标点的贡献比约为40.1%，较优化前提高约10.1%，激振器的贡献比约为59%，提高了评估的准确度。

图4 偏相干优化前后各传递路径对1#测点的

3 结论

本文通过偏相干优化方法优化了舰船噪声传递路径分析，解决了耦合噪声源合成时误差较大的问题，主要结论如下：

(1)本文根据舰船实际环境，模拟多种振源信号，结合偏相干分析，建立了舰船工况传递路径分析模型，并通过缩比舱段模型试验验证了该方法的有效性。

(2)基于源分离的工况TPA噪声合成结果要优于耦合信号合成结果，前者与实测值吻合较好，全频带合成误差均小于3 dB。