抓住本质 巧妙转化
—— 一道高考题的解题思路探索
2020-05-03 02:13唐骏
高中数学教与学 2020年3期
唐 骏
(江苏省邗江中等专业学校,225127)
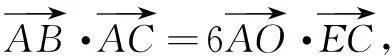
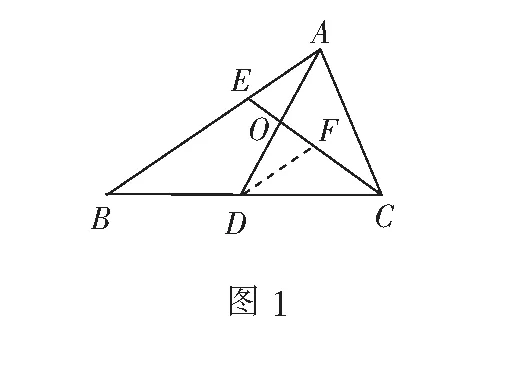
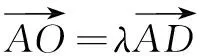
思路1 应用平面几何知识
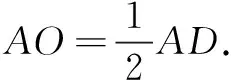
解 如图1,过点D作DF∥AB交EC于点F.
∵DF∥AB,D是BC的中点,
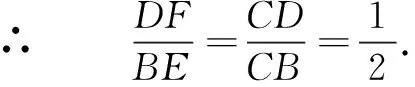
∵BE=2EA,
∴AE=DF.
∵DF∥AB,
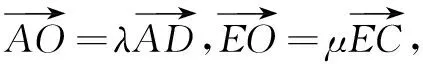
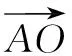
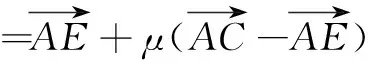
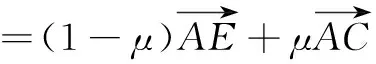

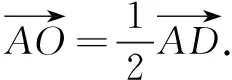
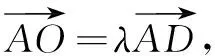
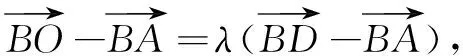
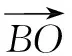
∵C、O、E三点共线,
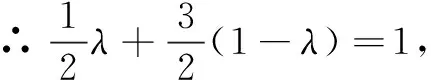
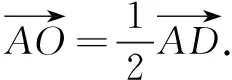
思路3 解析法
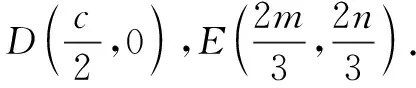
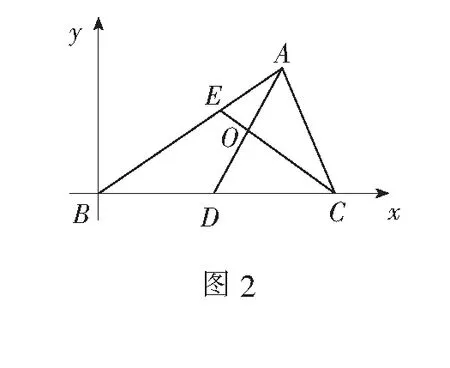
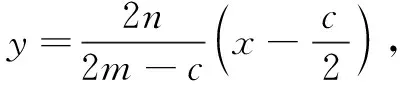
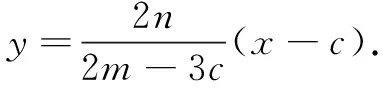
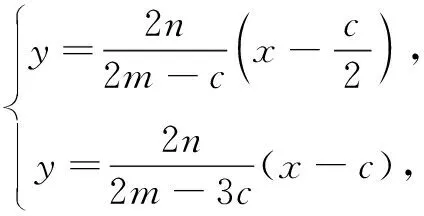
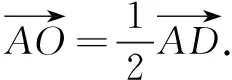
以上三种思路都是常规思路,平面几何方法中,平行线的作法还有很多,读者不妨自己试一试;向量法中,解法1利用的是平面向量基本定理,解法2利用的是向量共线定理;解析法中,建坐标系的方法并不唯一,也可以点D作为坐标原点、BC作为x轴建系.下面再介绍一种巧妙转化的思路,起点较低,但威力巨大,可很快得到点O是AD的中点.
思路4 面积法
解 设S∆AOC=S1,S∆ODC=S2,则S∆BOD=S2,S∆AOB=S1.
∵BE=2AE,
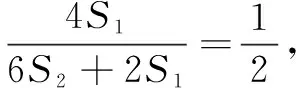
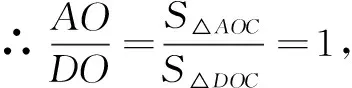
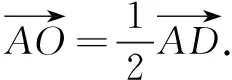
猜你喜欢
新高考·高一数学(2022年3期)2022-04-28
中学生数理化(高中版.高考数学)(2022年2期)2022-04-26
中学生数理化(高中版.高二数学)(2021年9期)2021-11-05
中等数学(2021年4期)2021-08-14
数理化解题研究(2021年19期)2021-08-05
中学生数理化·高一版(2021年5期)2021-07-21
中学生数理化·高一版(2020年11期)2020-12-14
新世纪智能(数学备考)(2018年9期)2018-11-08
高中生·天天向上(2018年1期)2018-04-14
中学生数理化·教与学(2016年8期)2016-08-23

