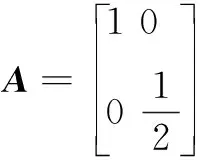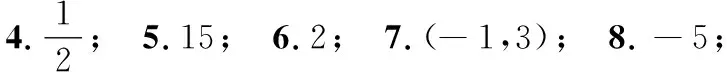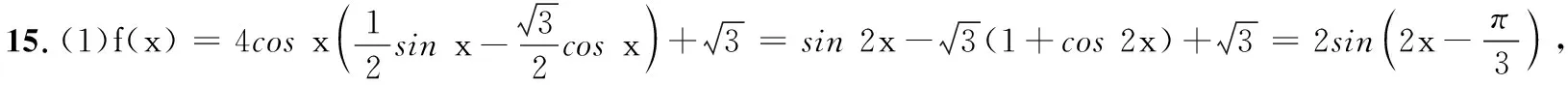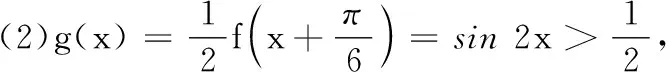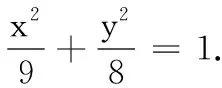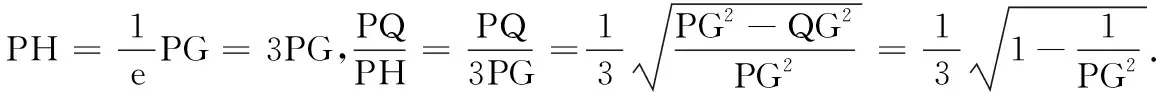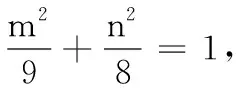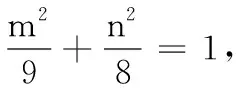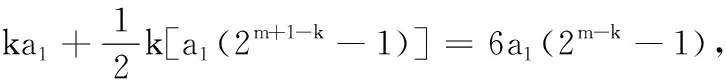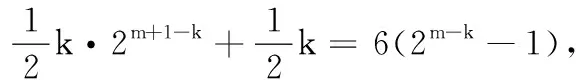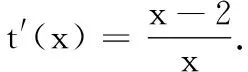高三数学综合测试
一、填空题(本大题共有14小题,每小题5分,共计70分.请将答案填写在答题卷相应位置)
1. 集合A={-1,0,2},B={x||x|<1},则A∩B=______.
3.命题p:“∀x∈R,x2+2x-3≥0”,命题p的否定:______.
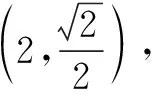
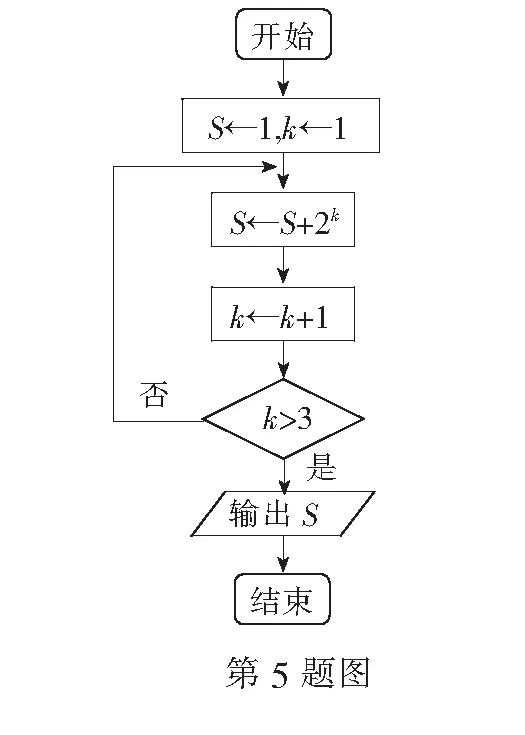
5.如图是一个算法流程图,输出的结果为______.
6.已知向量a=(1,1),b=(2,x),若a+b与a-2b平行,则实数x=______.
7.若函数y=f(x)的图象经过点(1,2),则函数y=f(-x)+1的图象必定经过的点的坐标是______.
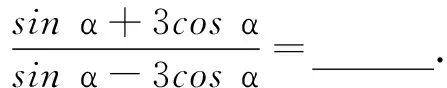
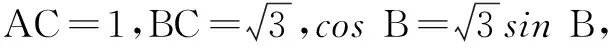

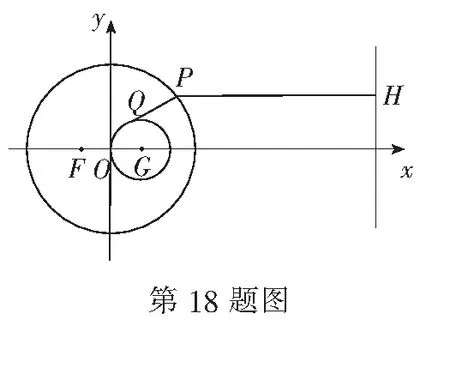
12.已知圆C:(x-1)2+y2=9,点B(-4,0).若存在不同于点B的定点A,使圆C上任意一点P到定点A、B的距离比为一个常数,则此常数值为______.
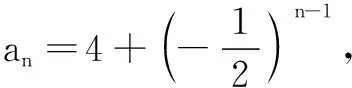
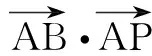
二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明、证明过程或演算步骤)
15.(本小题满分14分)已知函数

(1) 求f(x)的最小正周期;
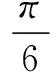
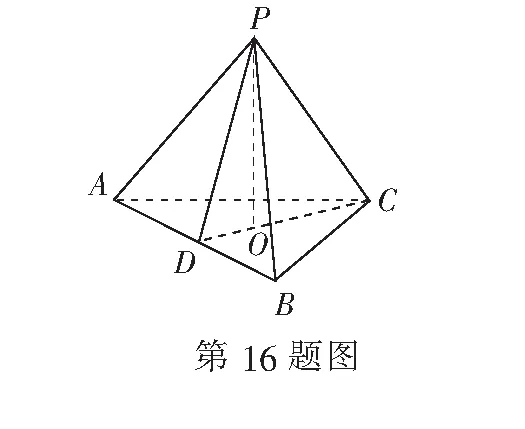
16.(本小题满分14分)在三棱锥P-ABC中,D为AB的中点.
(1) 若与BC平行的平面PDE交AC于点E,判断点E在AC上的位置,并说明理由;
(2) 若PA=PB,且∆PCD为锐角三角形,又平面PCD⊥平面ABC,求证:AB⊥PC.
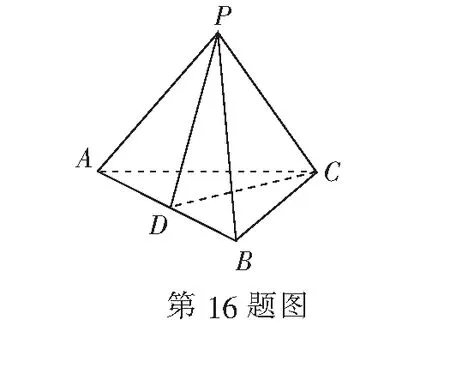

(1) 当AB沿正北方向时,试求商业中心到A、B两处的距离之和;
(2) 若要使商业中心O到A、B两处的距离和最短,请确定A、B的最佳位置.
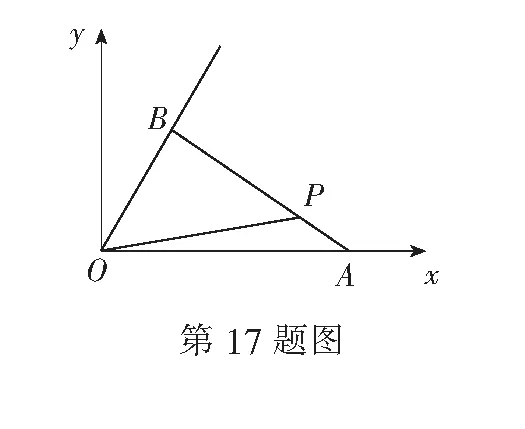
(1) 求椭圆的方程;
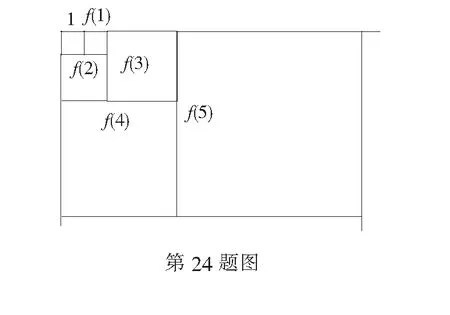
19.(本小题满分16分)设m个正数a1,a2,…,am(m≥4,m∈N*)依次围成一个圆圈.其中a1,a2,…,ak-1,ak(k (1) 若a1=d=2,k=8,求数列a1,a2,…,am的所有项的和Sm; (2) 若a1=d=2,m<2020,求m的最大值; (3) 是否存在正整数k,满足a1+a2+…+ak-1+ak=3(ak+1+ak+2+…+am-1+am)?若存在,求出k值;若不存在,请说明理由. 20.(本小题满分16分)已知函数f(x)=ex,g(x)=ax2+bx+c. (1) 若f(x)的图象与g(x)的图象所在两条曲线的一个公共点在y轴上,且在该点处两条曲线的切线互相垂直,求b和c的值; (2) 若a=c=1,b=0,试比较f(x)与g(x)的大小,并说明理由; (3) 若b=c=0,证明:对任意给定的正数a,总存在正数m,使得当x∈(m,+∞)时,恒有f(x)>g(x)成立. 附加题 (1) 求这3名学生选做A题的概率; (2) 设这3名考生中选做B题的学生个数为X,求X的概率分布列及数学期望. 24.(本小题满分10分)如图,平面上已有一个边长为1的正方形,现按如下规律作正方形:第一步向右作一个边长也为1的正方形;第二步向下以上面两个正方形的边长之和为边长作正方形;第三步向右以左面两个正方形的边长之和为边长作正方形,…记第n步所作正方形的边长为f(n),n∈N*. (1) 求f(1)f(3)-f2(2)和f(2)f(4)-f2(3)的值; (2) 试猜想f(n)f(n+2)-f2(n+1)的结果,并用数学归纳法证明. 参考答案 一、填空题 1.{0}; 2.-1; 3.∃x∈R,x2+2x-3<0; 二、解答题 16.(1)E为AC中点.理由如下:因为平面PDE∩平面ABC=DE,而BC∥平面PDE,BC⊂平面ABC,所以BC∥DE.在∆ABC中,因为D为AB的中点,所以E为AC中点. (2)因为PA=PB,D为AB的中点,所以AB⊥PD.又平面PCD⊥平面ABC,平面PCD∩平面ABC=CD,在锐角∆PCD所在平面内,过P作PO⊥CD,垂足为O,所以PO⊥平面ABC.因为AB⊂平面ABC,所以PO⊥AB. 由PO∩PD=P,PO、PD⊂平面PCD,知AB⊥平面PCD.又PC⊂平面PCD,所以AB⊥PC. 综上,商业中心到A、B两处的距离和最短为9km,此时OA=16km,OB=3 km. 答:A选地址离商业中心6 km,B离商业中心3 km为最佳位置. 解法2 设P(x,y),x∈[-3,3],则 (本题也可以直接求出轨迹方程后再说明圆心恰好在椭圆上) 19.(1)依题意ak=16,故数列a1,a2……,am即为2,4,6,8,10,12,14,16,8,4共10个数,此时有m=10,Sm=84. (2)由数列a1,a2,a3,……,ak-1,ak是首项为2、公差为2的等差数列,知ak=2k,而由a1,am,am-1,……,ak+1,ak是首项为2、公比为2的等比数列,知ak=2m+2-k,因此有2k=2m+2-k,k=2m+1-k,即k必是2的整数次幂. 由k·2k=2m+1知,要使m最大,k必须最大.又k (3)由数列a1,a2,a3,……,ak-1,ak是公差为d的等差数列知,ak=a1+(k-1)d. 而由a1,am,am-1……,ak+1,ak是公比为2的等比数列,得ak=a1·2m+1-k. 故a1+(k-1)d=a1·2m+1-k,(k-1)d=a1(2m+1-k-1). 又a1+a2+…+ak-1+ak=3(ak+ak+1+…+am-1+am),且am=2a1,则 即k·2m+1-k+k=6×2m+1-k-12, 显然k≠6,则 所以k<6,将k=1,2,3,4,5一一代入验证知,当k=4时,上式右端为8,要使等式成立,此时m=6即可. 综上,当且仅当m=6时,存在k=4满足题意. 20.(1)f(0)=1,f′(x)=ex,f′(0)=1,g(0)=c,g′(x)=2ax+b,g′(0)=b. (2)a=c=1,b=0时,g(x)=x2+1. 当x=0时,f(0)=1,g(0)=1,即f(x)=g(x). 当x<0时,f(x)<1,g(x)>1,即f(x) 当x>0时,令h(x)=f(x)-g(x)=ex-x2-1,则h′(x)=ex-2x. 设k(x)=h′(x)=ex-2x,则k′(x)=ex-2. 当x 综上,当x<0时f(x) (3)证法1 ①若0 ②若a≥1,f(x)>g(x),即ex>ax2,等价于x>ln(ax2),即x>2lnx+lna. 又t(x0)=e2a-2lne2a-lna=e2a-3lna-4>7a-3lna-4=4(a-1)+3(a-lna)>0,即存在m=ae2,当x∈(m,+∞)时,恒有f(x)>g(x). 综上,对任意给定的正数a,总存在正数m,使得当x∈(m,+∞),恒有f(x)>g(x). 综上,对任意给定的正数a,总存在m,当x∈(m,+∞)时,恒有f(x)>g(x). 附加题 21.设P(x,y)是曲线C1上任意一点,点P(x,y)在矩阵A对应的变换下变为点P′(x′,y′),则有 22.由ρ=4sinθ,得ρ2=4ρsinθ,所以x2+y2-4y=0,即圆C方程为x2+(y-2)2=4. 23.(1)记“这3名学生选做A题”为事件C,则 故变量X的概率分布列为 X0123P18383818 24.(1)依题意,f(1)=1,f(2)=2,f(3)=3,f(4)=5.故f(1)f(3)-f2(2)=-1,f(2)f(4)-f2(3)=1. (2)猜想:f(n)f(n+2)-f2(n+1)=(-1)n,n∈N*. ①当n=1时,f(1)f(3)-f2(2)=-1,结论成立; ②假设n=k时,结论成立,即f(k)f(k+2)-f2(k+1)=(-1)k. 由题意,知f(n+2)=f(n+1)+f(n)对n∈N*恒成立.则当n=k+1时, f(k+1)f(k+3)-f2(k+2) =f(k+1)[f(k+1)+f(k+2)]-f2(k+2) =f(k+1)f(k+2)+f2(k+1)-f2(k+2) =f(k+2)[f(k+1)-f(k+2)]+f2(k+1) =f2(k+1)-f(k)f(k+2) =-[f(k)f(k+2)-f2(k+1)] =(-1)·(-1)k =(-1)k+1, 即当n=k+1时,结论成立. 综合①、②,恒有等式f(n)f(n+2)-f2(n+1)=(-1)n,n∈N*.