处理数列问题的几种意识

刘 岩

(黑龙江省鸡西市一中，158100)

数列是高中数学的核心知识,尽管在近几年的高考中有些弱化,但仍是高考的必考考点.本文就处理数列选择题应体现出的数学意识加以盘点,以期能对大家的学习有所启发和帮助.

一、整体意识

例1 若数列{an}满足a1=1,an+1an=2n(n∈N*),则S2 016=( )

(A)22 016-1 (B)3·21 008-3

(C)3·22 018-1 (D)3·21 007-2

评注 通过整体处理,避免了分别求数列奇数项和与偶数项和的运算,增加了思维量,减少了计算量.

变式 数列{an}满足an+1+(-1)na=2n-1,则{an}的前60项和为( )

(A)3 690 (B)3 660

(C)1 845 (D)1 830

解 由an+1+(-1)nan=2n-1，可得an+2=(-1)nan+1+2n+1=(-1)n[(-1)n-1an+2n-1]+2n+1=-an+(-1)n(2n-1)+2n+1,即

an+2+an=(-1)n(2n-1)+2n+1.

①

进而也有

an+3+an+1=-(-1)n(2n+1)+2n+3，

②

①+② 可得an+an+1+an+2+an+3=-2(-1)n+4n+4.于是，a4k+1+a4k+2+a4k+3+a4k+4=16k+10(k∈N).从而有

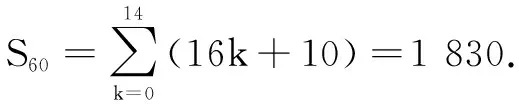
二、函数意识

例2 等差数列{an}(n∈N*)的前n项和为Sn,已知S10=0,S15=25,则nSn的最小值为( )

(A)-48 (B)-49

(C)-50 (D)0

解 由{an}是等差数列，可设Sn=an2+bn(a、b∈R).

评注 数列的实质是定义域为正整数集(或其有限子集)的一列函数值,因此很多处理函数问题的方法可以类比应用到数列相应问题中去.

三、讨论意识

(A)[-2,3] (B)[-2,3)

(C)(-2,3] (D)(-2,3)

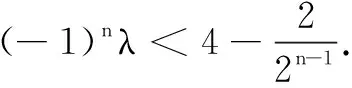
评注 分类讨论是数学中常用的解题策略,本题中出现了因子(-1)n,故分类的“度”就定位在“n分奇数和偶数”.

四、放缩意识

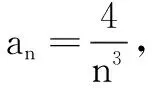
(A)4 (B)5 (C)6 (D)7

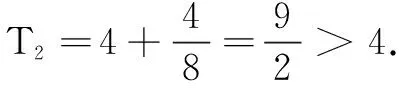
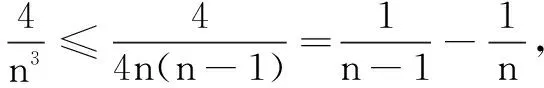
综上，整数m的最小值为5，选B.

评注 裂项是处理数列放缩题最常用的方法之一,解题的关键是要掌握好放缩的“度”,如何掌握这个度还要靠平时的积累.

五、周期意识

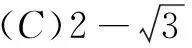
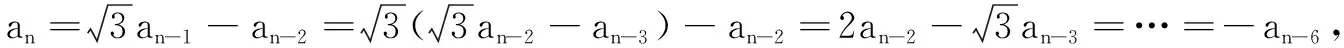
评注 涉及数列周期问题的题目很多,解题的基本思路是写出有限项后,猜出周期当然为了缜密,必要时还需进行证明.

六、数形意识

(A)[-5,-4] (B)[-4,-3]

(C)[-5,-3] (D)非上述答案

解 依题意，cn=max{an,bn},且c5是数列{cn}的最小项.

若c5=a5,如图1,则必须且只需b5≤a5≤b6,即5+k≤25-5≤6+k,解得-5≤k≤-4;若c5=b5,如图2,则必须且只需a5≤b5≤a4,即25-5≤5+k≤25-4,解得-4≤k≤-3.

综上，-5≤k≤-3.选C.

评注 借助数形结合,让这个较复杂题目的解决变得直观、清晰；同时，上述解题流程也体现了分类讨论的数学思想

七、递推意识

例7 已知数列{an}满足a1=1,a2=2,a3=3,a4=4,a5=5,且当n≥5时,有an+1=a1a2…an-1.若数列{bn}满足对任意的n∈N*,有bn=a1a2…an-a21-a22-…-a2n,设数列{bn}的前n项和为Sn,则S24=( )

(A)-17 (B)-276

(C)1 093 (D)1 110

解 计算可知b1=0,b2=-3,b3=-8,b4=-6，b5=65.当n≥5时,bn+1-bn=a1a2…an(an+1-1)-a2n+1=(an+1+1)(an+1-1)-a2n+1=-1,即从b5开始,数列{bn}是公差为-1的等差数列，可得bn=70-n(n≥5).

评注 本题的设计背景比较新颖,能借助已知条件挖掘到递推式bn+1-bn=-1是破解该题的关键,需要良好的数学素养.

八、迁移意识

(A){Sn}单调减

(B){Sn}单调增

(C){S2n-1}单调减,{S2n}单调增

(D){S2n-1}单调增,{S2n}单调减

解 首先证明∆AnBnCn的周长为定值3a1.

评注 注意到∆AnBnCn的周长为定值,将问题迁移转化成椭圆焦点三角形的面积问题,另辟蹊径,说理过程令人耳目一新.当然该题也可借助特值法来求解.

以上盘点了处理数列题时应体现出的几种数学意识,当遇到一个具体的数列问题时,到底应体现哪种或哪几种数学意识,并没有一成不变的规律,还需依据题目的特点以及平时的积累，具体问题,具体分析,且不可生搬硬套!