GPS垂向年周期运动的精确获取与方法评估*

李经纬，占 伟，梁洪宝，王 勇，郭南男

(1.中国地震局第一监测中心，天津 300180；2.天津城建大学 地质与测绘学院，天津 300384)

0 引言

近年来，我国许多区域(如川滇地区)GPS垂向存在显著的周期性运动(其中年周期运动最为突出)(张飞鹏等，2002；刘任莉等，2013；梁洪宝等，2015；王岩等，2018)，盛传贞等(2014)认为滇西地区GPS坐标变化时间序列的垂向分量中，普遍包含有明显的年周期非构造形变波动，高值可达12 mm；Zhan等(2017)基于2010—2015年云南27个GPS连续站垂向时间序列得出该时段云南地区GPS连续站垂向年周期振幅平均值为9.7 mm，认为云南地区季节性的降雨与GPS垂向年周期运动相关性较好。GPS垂向周期性运动研究有重要的研究意义和实际应用价值，目前我国GPS流动观测的观测数据量太少、无法消除周期性运动的影响，导致得到的垂向线性运动速率结果精度不高，GPS垂向速度场应用较少(方颖等，2014；朱爽等，2017；李长军等，2018)，因此精确获取垂向周期性运动信息能够提高GPS流动观测的垂向线性运动速率精度，极大地促进GPS垂向速度场的应用。

一些学者使用了不同的方法获取GPS流动站的垂向周期性运动参数(Liangetal，2013；占伟等，2016)，但是对这些方法的效果评估、分析较少，尤其是中国大陆幅员广阔，不同区域影响垂向周期性运动的主要因素不一，不同方法的适用性也不同，因此对GPS垂向周期性运动参数获取方法进行全面的评估十分必要。本文以云南为研究区域，选用4种垂向年周期运动参数获取方法，以研究区域内2010—2015年陆态网络26个GPS连续站观测数据得到的垂向年周期运动结果，评估这4种方法的效果，综合评估各方法的优缺点，对不同的区域如何获取垂向年周期运动参数给出建议。

1 方法介绍

常用的垂向年周期运动获取方法分为2类，一类是根据一些物理模型(如负荷模型或者GRACE)直接求解某一空间位置的垂向年周期运动参数；另一类是对区域内GPS连续站实测的垂向年周期运动参数进行空间内插。本文选用4种GPS垂向年周期运动获取方法，分别为：

(1)方法1：负荷模型方法。地球表面各种负荷变化是GPS垂向周期性运动的主要影响因素，而在云南地区，陆地水的质量变化是该区域GPS垂向周期性运动的主要影响因素(姜卫平等，2013；Jiangetal，2017)，因此笔者从EOST Loading Service(1)http：//loading.-ustrasbg.fr/ditrf_form.php.下载了2010—2015年全球陆地水文负荷模型(GLDAS)解算的垂向位移格网数据(CM)，数据空间分辨率为0.5°×0.5°，时间分辨率为3 h。基于云南地区各格网点垂向位移时间序列，采用线性+年周期+半年周期方法拟合得到各格网点年周期运动正弦波振幅A和余弦波振幅B，为了与GPS连续站结果比对，采用多核函数法空间插值获取云南地区26个GPS连续站所在空间位置的年周期运动正弦波振幅A1和余弦波振幅B1。

(2)方法2：GRACE模型方法。利用GRACE数据给出的地球重力场球谐系数(Bruinsmaetal，2010)和负荷勒夫数(Farrell，1972)，可以根据弹性负荷形变理论获取负荷引起的形变信息(Wahretal，1998；Kusche，2005；Fuetal，2012)。笔者按照Hao等(2016)的方法处理了CSR提供的GRACE-RL05数据：使用GCM05S模型去掉平均重力场；用SLR观测的C20项系数项和一阶项系数替换模型中相应值；采用高斯滤波方法去除高阶模型噪声，最终得到了26个GPS连续站所在空间位置的垂向位移结果(采样率为每月)，采用线性+年周期+半年周期方法拟合得到各GPS连续站的年周期运动正弦波振幅A2和余弦波振幅B2。

(3)方法3：空间加权法。基于Zhan等(2017)给出的2010—2015年云南地区26个GPS连续站垂向位移时间序列(进行了预处理，包括去除了仪器更换等原因产生的突跳)，采用线性+年周期+半年周期方法拟合得到各连续站年周期运动正弦波振幅A0和余弦波振幅B0。对某一个GPS连续站(记为插值点)，根据其余25个连续站的年周期运动正弦波振幅A0和余弦波振幅B0，采用空间加权法插值得到插值点的年周期运动正弦波振幅A3和余弦波振幅B3：

(1)

式中：dj为插值点与第j个GPS连续站的水平距离；A0j和B0j为第j个GPS连续站的年周期运动正弦波和余弦波振幅。

(4)方法4：多核函数法。该方法计算过程与方法3类似，对于每一个GPS连续站，都是其它25个GPS连续站垂向年周期运动参数(A0和B0)空间插值得到插值点的年周期运动参数(A4和B4)，唯一的区别就是空间插值采用多核函数法。多核函数法由美国Hardy(1971)提出，其空间插值计算过程如下：

(2)

式中：f(λ，φ)为多核函数；sj(λ，φ，λj，φj)为多核函数；dj1.1为球面上2点间的大地线长度(单位为km)；cj为待定系数(杨国华等，2012)。将所有可用的数据点作为核函数点，可以获得数学解析式，计算任一空间位置的结果。

2 效果评估

本文依据4种方法与GPS连续观测得到的垂向年周期运动振幅差异和一致性评估各方法的效果。

2.1 振幅差异

图1给出了GPS连续观测得到的垂向年周期运动与4种方法结果之间的差异，从中可以看出：①方法1和方法2与GPS连续观测的垂向年周期运动振幅差异较大，且方向上大体一致，说明这2种方法得到的垂向年周期运动与GPS连续观测结果存在系统的时间差；②方法3和方法4与GPS连续观测的垂向年周期运动振幅差异比前2种方法偏小，且差异的方向较为杂乱、没有表现出较为明显的规律，说明后2种方法更为接近GPS连续站得到的垂向年周期运动。表1给出了4种方法与GPS实测结果的振幅差异统计结果，4种方法与GPS连续站实测的振幅差异平均值分别为4.97，3.31，1.38，1.43 mm，而26个GPS连续站实测的垂向年周期运动振幅平均值为9.87 mm，可见方法1和方法2与GPS实测结果的差异较为显著(分别达到实测振幅的50.35%和34.95%)。

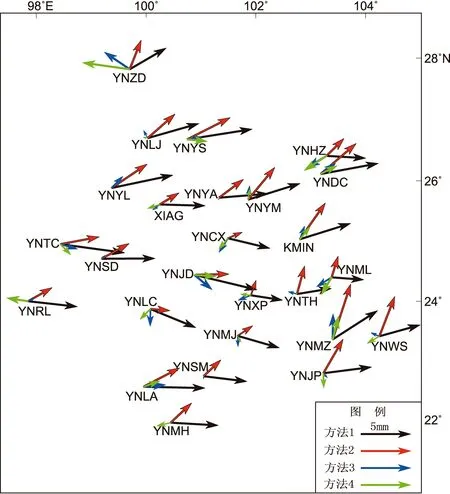
图1 4种方法与GPS连续观测的年周期运动差异Fig.1 Difference of crustal annual motions between continuous GPS and four methods

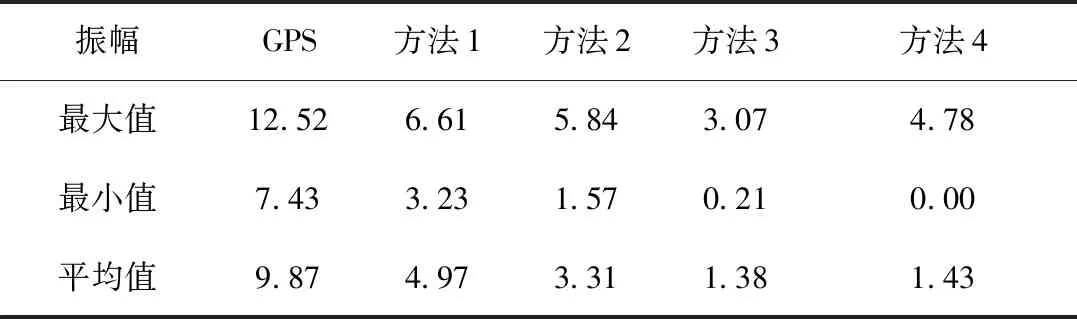
表1 4种方法与GPS连续观测的年周期运动振幅差异Tab.1 Difference of crustal annual motion amplitude between continuous GPS and four methods (单位：mm)

2.2 一致性评估

本文用WRMS减速比(Fu，Freymueller，2012)来评估各方法得到的垂向年周期参数与GPS连续站时间序列的一致性，定义为：

(3)

式中：RatioW表示WRMS减速比；WRMSG是2010—2015年26个GPS连续站垂向时间序列去除线性后WRMS值；WRMSm是GPS垂向时间序列去除线性后再去除年周期运动后的残差WRMS值；WRMSf是GPS垂向时间序列去除线性和年周期运动后的残差WRMS值。

RatioW能够反映GPS连续站的垂向时间序列和各方法求得的年周期运动相位和振幅的一致性。图2给出了4种方法的RatioW结果，从中可以看出后2种方法的绝大多数测站RatioW大于0.9，远远优于前2种方法，但方法3和4中YNZD站RatioW相对较小(图2c，d)。表2给出了4种方法的RatioW统计结果，其平均值分别为0.70，0.84，0.95，0.94，表明方法3和4效果大体相当，优于方法1和2，相对而言，方法2的效果优于方法1。

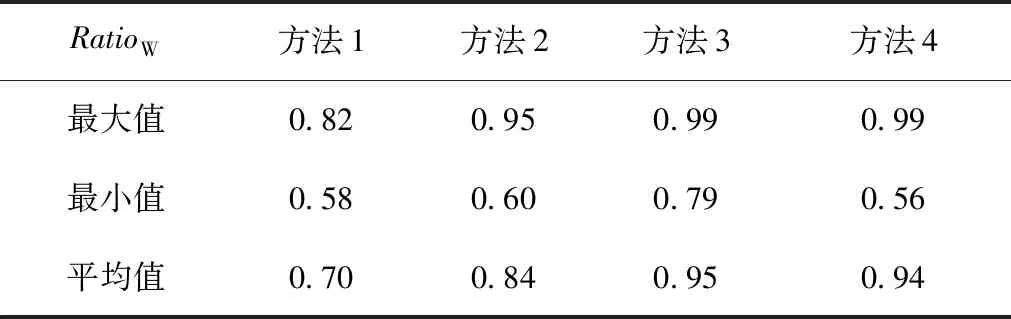
表2 4种方法的RatioW统计结果Tab.2 Static results of WRMS reduction ratio of the four methods

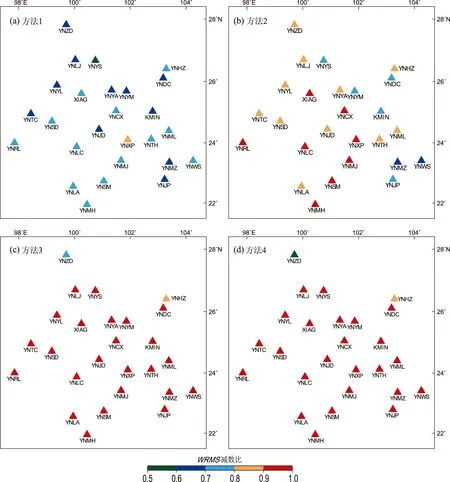
图2 4种方法的RatioW
Fig.2 WRMS reduction ratio of four methods

3 讨论

从4种方法的整体评估结果可以看出，方法1和方法2得到的垂向年周期运动无论是振幅大小还是运动方向，均与GPS连续观测的结果存在较大的差异，而方法3和方法4利用GPS连续观测进行空间内插，得到的垂向年周期运动与GPS连续观测结果一致性较好。

由于全球负荷模型是基于全球观测数据建立的模型，模型建立时使用的中国大陆范围内的实测数据较少，因此在中国大陆尤其是云南这样的局部区域与实测数据一致性较差，使得全球负荷模型得到的垂向年周期运动与GPS实测结果差异较大。

方法2的GRACE模型得到的垂向周期性信号反映的是区域空间尺度达300～400 km的整体形变，GPS垂向周期性信号不仅反映了区域整体形变，还可能叠加一些局部效应(姜卫平等，2013；Yanetal，2016)，因此GRACE得到垂向年周期运动振幅与GPS实测结果存在一定差异。

需要说明的是：不同的全球负荷模型(方法)在中国大陆的符合程度存在差异，同时GRACE数据处理方法(方法2)也存在一定的差异，这2种方法在中国大陆的应用优化值得更为深入的研究。

云南地区GPS连续站较多，且区域垂向周期性运动空间一致性较好，各点的垂向年周期运动无论是振幅大小还是初相均较为一致(Zhanetal，2017)，因此2种空间插值的方法效果要优于前2种方法，而且方法3和方法4评估结果大体相当，说明只要区域内垂向周期性运动空间一致性较好，即使选用不同的空间内插方法，对结果影响不大。值得注意的是，在26个GPS连续站中，YNZD站空间位置最为突出(最北端)，周边的GPS连续站与之距离较远，因此在方法3和方法4中，该站利用其余25个测站空间内插得到的垂向年周期运动参数与实测结果差异最大，这说明2种空间插值方法要求GPS连续站的分布尽量均匀。

上述4种方法各有优劣，虽然在本文的实验中，方法1和方法2的效果不如方法3和4，但前2种方法可以直接利用已有的全球负荷模型和GRACE给出的任意一点垂向位求得任意一点的垂向年周期运动。方法3和方法4虽然效果较好，但是对区域内GPS连续站的数量和分布有一定的要求，在实际应用中可能受到限制。事实上，目前中国大陆仍有一些区域GPS连续站较少，以陆态网络为例，目前中国大陆范围内只有260个GPS连续站，平均站间距为130 km，仅少数区域如首都圈、南北地震带GPS连续站密度相对较高(云南地区GPS连续站平均站间距79 km)，在西藏、东北、华南等区域GPS连续站较少，因此方法1和2在这些GPS连续站较少的区域仍然有一定的实际使用价值。

4 结论

本文选用4种获取GPS垂向年周期运动参数的方法，以GPS连续观测得到的垂向年周期运动结果评估了这4种方法的效果，结果表明：由于云南地区GPS连续站较多且垂向年周期运动空间一致性较好，利用GPS连续观测的垂向年周期运动参数进行空间插值(方法3和方法4)都能够取得较好的效果，GRACE模型方法(方法2)效果稍差，负荷模型方法(方法1)效果最差，因此对于获取区域内(如GPS流动站)的垂向年周期运动参数，在GPS连续观测站较多的区域，建议采用空间加权法(方法3)或者多核函数法(方法4)；在GPS连续站较少的区域，建议采用GRACE模型方法。

由于本文的主要目的是验证垂向年周期运动信息的构建模型有效性，因此只考虑了季节性运动中最主要的年周期运动，但本方法也适用于其它周期性运动(如半年周期运动)。

感谢NASA提供GRACE数据、EOST提供全球陆地水文负荷模型垂向位移数据。