一道含参函数问题的两种解法的比较

■梁立扬(指导老师:褚人统)

例题已知a＞0,f(x)=ln(2x+1)+2ax-4aex+4。当a=1 时,f(x)的最大值为0。若函数f(x)的零点个数为2,求a的取值范围。

解法一：(常规解法),当a＞0,且时,f″(x)＜0,所以f′(x)在上为减函数。

①当a=1时,f(x)只有唯一零点。

②当0＜a＜1 时,f(0)=4-4a＞0,即f(x0)＞f(0)＞0,此时有2个零点。

③当a＞1 时,2a-4aex0=0。

f(x0)=ln(2x0+1)+2ax0-4aex0+。

又有f′(0)=2-2a＜0,故。

令g(x)=ln(2x+1)+2ax-,则g′(x)=,故g(x)在定义域内单调递增。

而g(0)=2-2a＜0,故g(x)＜0,于是f(x0)＜0,所以当a＞1时不存在零点。

解法二：(利用偏导数求解)令z=f(x)=ln(2x+1)+2ax-4aex+4,则za=z′a=2x-4ex(za以a为自变量,zx以x为自变量),表示固定某x时,a方向斜率的增速)。

当x=x0时,4ex0为一常数且小于0,,所以原式z(a)递减(a为自变量,x=x0为常数)。

当a=1时,f(x)max=0。

所以当a=1时,f(x0,a)≤0。

又f(x)=ln(2x+1)+2ax-4aex+4(a＞0),并且,

所以仅当0＜a＜1 时,存在f(x)＞0(x=x0)(x为自变量,a为常数),当0＜a＜1时,存在有2个零点(如图1所示)。

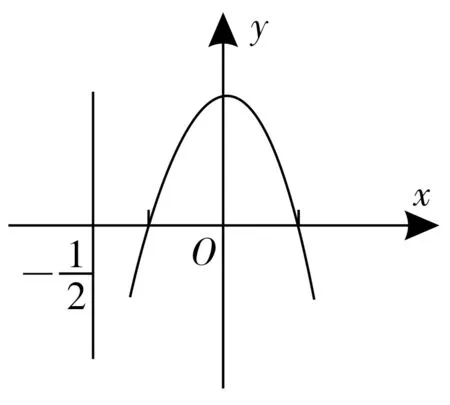
图1

总结：两种方法相比较,利用偏导数求解时的运算过程更加简洁。很多高中数学问题都可以采用多种方法解决,所以同学们在做题时,不能仅仅满足于一道问题的解答,而应该关注同一道问题可以采用哪些不同的方法解答,并比较不同解法的优缺点,拓展思维的宽度。同时同学们也不要局限于对课本知识的学习,也可适当关注导数、泰勒公式、柯西不等式等这些高等数学知识,因为在解决数列放缩、不等式证明等问题时,通常可以使大家站在更高的角度看问题,更好地解答问题。