变速器齿轮系统振动噪声激励响应研究

朱春华 杨亚楠

(河北建筑工程学院，河北 张家口 075000)

0 引 言

噪声是汽车的运转性能指标之一，随着国六的发布，国家对汽车噪声限值的要求愈加严格，加之人们对汽车乘坐舒适性的要求越来越高，振动和噪声成为了汽车主要性能指标之一.而随着发动机等降噪技术的不断发展和提高，变速器振动噪声成为了汽车的主要噪声源.汽车变速器是由一系列的齿轮传动系统组成的，其振动噪声的激励源可以分为外部激励和内部激励两大类，其中内部激励主要有齿轮啮合误差激励、啮合刚度激励和啮合冲击激励，它们构成了变速器振动噪声产生的主要影响因素.因此，研究变速器齿轮系统振动噪声的激励响应能够为汽车振动噪声的发生机理及变速器减振降噪措施的研究奠定基础.

1 齿轮系统激励响应分析计算

1.1 齿轮系统误差激励

齿轮副的啮合误差激励是齿轮副工作过程中的一种主要动态激励，所谓的啮合误差激励主要表现为轮齿无法按照理想的齿轮齿形进行啮合，从而导致瞬时传动比骤变，齿与齿之间发生碰撞，不能按照设计的定传动比平稳传动.

通常来说，齿轮时变啮合误差的数值可用以下四种方式表示：以实际测量的误差数据表示；以实测得到的误差函数曲线表示；利用傅里叶级数表示；利用简谐函数表示[1].本文在明确齿轮的设计精度等级所对应的轮齿偏差前提下，采用第四种表示方式进行计算并对误差曲线进行模拟.

齿轮啮合误差是随时间不断变化的，这种激励导致齿轮啮合时产生了位移型激励，其影响综合反映在齿轮啮合线方向上：

e(t)=e0+ersin(πt/Tz+φ)

(1.1)

式中：e(t)——齿轮的基节误差和齿形误差；

e0——齿轮误差的常值，通常取e0=0；

er——齿轮误差的幅值；

t——时间；

Tz——齿轮的啮合周期，Tz=εr×60/nz；

φ——相位角，取φ=0.

由于基节误差和齿形误差这两个随机变量均服从正态分布，两者想要同时达到极限偏差几乎是不可能的，因此，对幅值er的计算可同时考虑基节误差和齿形误差：

(1.2)

式中：fph——齿轮的基节误差；

ff——齿轮的齿形误差.

一档齿轮副、二档齿轮副、主减速齿轮副的齿轮加工精度均为6级，重点考察公差组II，查阅资料可得er=44μm.主从动齿轮齿根到齿顶的误差服从正弦分布，在Matlab软件中编制程序，各齿轮副误差曲线如图1.1-图1.3所示.由图可以明显看出，齿轮副的啮合误差是随着啮合时间的变化而变化的，正是齿轮啮合误差的波动性导致了齿轮副的瞬时传动比发生突变，使齿轮副齿与齿之间产生碰撞与冲击，引起齿轮传动系统的动态啮合激励，从而使变速器产生了相应的振动与噪声.

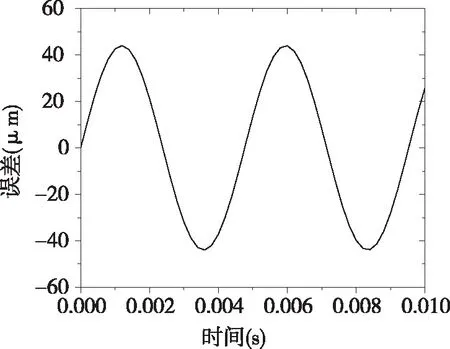
图1.1 一档齿轮副误差曲线

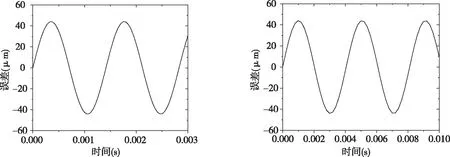
图1.2 二档齿轮副误差曲线 图1.3 主减齿轮副误差曲线

1.2 齿轮系统刚度激励

齿轮的啮合刚度激励指的是齿轮啮合过程中由于啮合刚度的时变性而产生的动态激励现象，该激励也是齿轮传动最主要的动态激励形式之一[2].

齿轮在传递载荷时，齿轮的啮合刚度是随着时间进行周期性变化的.这是因为参与啮合的齿轮存在弹性变形，并且参与啮合的齿对数在啮合过程中会随着齿轮滚动角的变化而发生变化.齿轮啮合刚度激励是一种参数形式的激励，其周期性变化可以在弹性力项的时变系数中反映出来.乘用车变速器传动齿轮大多为渐开线斜齿轮，轮齿的啮合是从一端开始并逐步延展至整个齿面，直至啮合结束时从另一端脱离，因此其接触线是以“点-线-点”变化的，斜齿轮的啮合综合刚度是在某一均值下随时间周期性微小波动变化的.

齿轮的时变啮合刚度研究的是齿轮的微变形，现有的实验条件难以进行测量，因而齿轮时变啮合刚度的研究大部分是基于的理论分析和数值计算.本文采用经验算法对斜齿轮刚度进行计算，可以得到齿轮副啮合过程中的刚度，较好地反映一对齿轮副在任意啮合位置上精确的啮合刚度值，便于进行分析.

齿轮副啮合刚度随时间的变化规律为：

(1.3)

式中：Kp——节点处的刚度；

Tz——齿轮的啮合周期；

ε——齿轮副的总重合度；

εα——齿轮副的端面重合度；

mn——法向模数；

H——全齿高，H=2.25mn.

式1.3得到的刚度值为在总齿宽上发生每微米形变需要的力，为方便观察分析，将主动齿滚动角作为自变量，国际标准定义的刚度作为因变量，对齿轮副轮齿啮合时的刚度变化曲线进行绘制，如图1.4-图1.6所示.

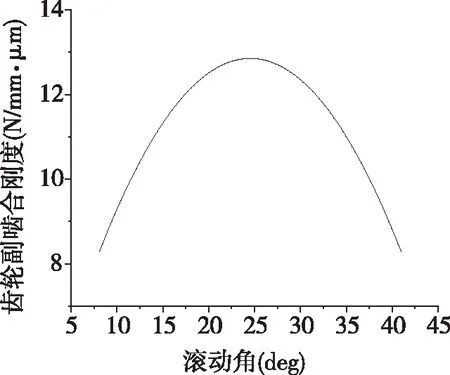
图1.4 一档齿轮副啮合时变刚度曲线

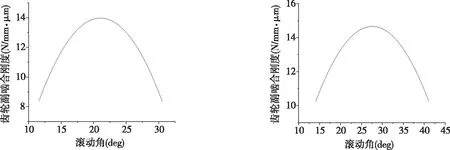
图1.5 二档齿轮副啮合时变刚度曲线 图1.6 主减齿轮副啮合时变刚度曲线

1.3 齿轮系统啮合冲击激励

齿轮啮合传动的过程中，实际基节与理论基节由于齿轮制造误差、受载变形等原因并不相等，该误差称为基节误差，如图1.7所示.两齿轮啮合时由于基节误差的存在会有合成基节误差的产生，使啮入时啮合点的位置相较于理论情况有所偏离，齿轮对会提前啮入，传动比突变，形成啮入冲击力[3].齿轮啮合即将结束时，啮合点的位置同样会偏离理论位置，产生啮出冲击力.啮出冲击产生的机理与啮入冲击相同，而相较于啮出冲击，啮入冲击对振动特性的影响更加显著.啮合冲击力则是对啮入冲击力和啮出冲击力的合称，该激励也是引起齿轮传动系统振动噪声的激励源之一.

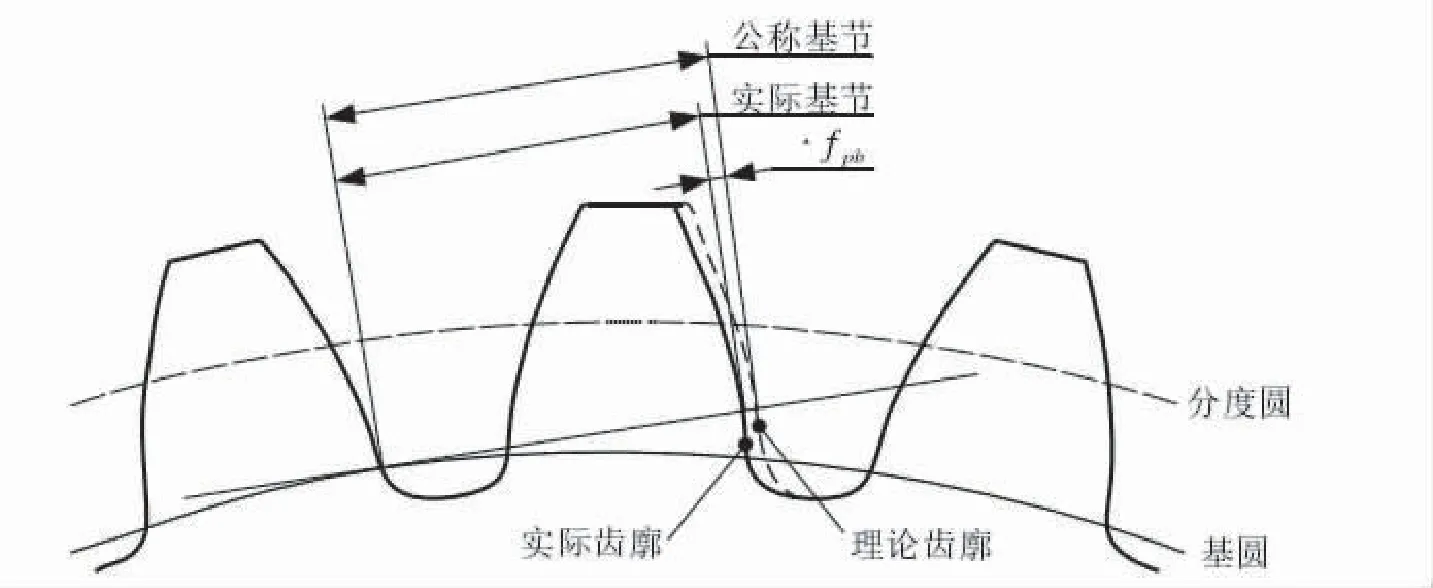
图1.7 基节误差示意图

2 传递误差理论

在上述三种形式的内部激励中，根据激励的特点可以将其分为位移型激励和冲击力型激励，其中齿轮刚度激励和误差激励属于位移型激励，冲击力型激励则是由啮合冲击激励产生的.对于位移型激励，Harris于1958年首次提出传递误差的概念，将载荷作用下轮齿的变形和齿轮误差两者进行了合并分析，为位移型动态激励的研究提供了重要的工具和手段.自传递误差概念提出以来，大量的试验与研究都表明了其与齿轮系统动态响应具有重要的关联性，是齿轮振动噪声研究中被广泛认可的最为重要的激励源.

理想情况下齿轮系统在运转时，相互啮合的齿轮是完全共轭的，从动齿轮会随着主动齿轮的转动而转过一定角度，但在实际情况下，由于受位移型激励等影响，主动齿轮转过一定角度后，从动齿轮的实际转动角度会与理论上有一定差别，该偏差即为传递误差，因此传递误差(Transmission Error,TE)定义为从动齿轮理想转角与实际转角的偏差值，根据定义，其计算公式为：

(2.1)

式中：θ1、θ2——主动齿轮、从动齿轮转动角度；

z1、z2——主动齿轮、从动齿轮齿数.

由以上计算分析及相关研究[4-5]可知，传递误差所代表的位移型激励是变速器振动噪声产生的最为主要的原因，因此，研究降低变速器振动噪声的措施时，应主要针对位移型激励研究其产生机理，主要目标是降低齿轮副传递误差，实现对汽车变速器减振降噪的目的.

3 结 论

本文对各内部动态激励：齿轮系统误差激励、齿轮系统刚度激励以及齿轮系统啮合冲击激励进行了理论研究和进一步的分析计算，并根据传递误差理论，得出位移型激励(齿轮刚度激励和误差激励)是变速器振动噪声产生的最为主要的原因.本研究能够为汽车振动噪声的发生机理及振动噪声的控制研究提供技术支持.