一维化学势调制的p波超导体中的拓扑量子相变*

武璟楠 徐志浩† 陆展鹏 张云波

1) (山西大学, 理论物理研究所, 太原 030006)

2) (量子光学与光量子器件国家重点实验室, 太原 030006)

本文研究了一维公度势和非公度势调制下的p波超导量子线系统的拓扑相变.在公度势调制下, 通过计算 Z2 拓扑不变量确定系统的相图, 指出系统的拓扑相变强烈地依赖于调制参数 α 和相移 δ.在非公度势调制下, 以为例, 计算系统的低能激发谱、 Z2 拓扑不变量以及逆参与率等, 发现 p 波配对强度 ∆ ∈(0,0.33) 时, 系统存在拓扑非平庸超导相, 拓扑平庸超导相和拓扑平庸局域相的转变.而当p波配对强度 ∆ >0.33 时, 系统存在拓扑非平庸超导相和拓扑平庸局域相的转变.

1 引 言

早在上世纪30年代, Majorana求解了Dirac相对论协变的电子运动方程, 发现了一种不带电荷的费米子, 它的反粒子是其自身.人们为了寻找它的踪迹一直在不懈地努力, 然而最终Majorana零模在凝聚态物理中被发现, 并成为重要的研究课题[1−5].超 导 体 系 中 U (1) 规 范 对 称 性 的 破 缺 为Majorana费米子的产生提供了可能性, 人们已经在具有强自旋-轨道耦合的半导体纳米线[6−10], 磁性原子链[11−13], 平面约瑟夫森结[14−16]以及常规超导体和拓扑绝缘体[17−19]的界面等体系中发现了它的存在.另一方面由于Majorana费米子具有局域性且满足非阿贝尔统计[20−22]等特性, 使得它成为实现容错拓扑量子计算[5,23]最有力的竞争者.由于拓扑量子计算的巨大应用前景, 使得Majorana费米子相关性质的研究越来越被人们重视.特别是近年来, 随着冷原子技术的发展, 人们发现通过周期驱动光格子可以实现物质拓扑态[24−26], 通过周期驱动具有p波配对的超导量子线, 有可能会产生额外的π模[27].通过多个时间周期驱动的Kitaev链产生了可以支持Majorana零模的新区域, 对Majorana费米子的寻找提供了理论基础[28].拓扑相最初是在厄密系统中发现的, 但人们对非厄密系统中拓扑相的研究也存在很大的兴趣[29−33].由于Majorana零模可以在非厄密体系中出现且可以持续存在, 其对环境具有很强的鲁棒性, 为更好地研究 Majorana 费米子提供方法.最近, Wu 等[34]阐述了实现非阿贝尔编织的一种新途径, 利用Jackiw-Rebbi零模也可以实现非阿贝尔编织,Jackiw-Rebbi零模不具有Majorana零模的自共轭特性, 其可以出现在非超导体系中.Jackiw-Rebbi零模的研究为拓扑量子计算提供了新的思路.有趣的是, Majorana零模可以被认为是Jackiw-Rebbi零模在具有粒子-空穴对称性时的特例[35,36].

Kitaev链是研究Majorana费米子的重要模型, 在此基础上人们意识到通过对Kitaev链的调制可以极大地改变系统的拓扑相变过程.如Lang和Chen[37]研究了周期性调制对Majorana费米子产生的影响, 他们发现随着调制强度的增大, 拓扑非平庸超导相可能会被破坏.由于Majorana零模的稳定性受到超导能隙的保护, 因此在加入周期调制化学势的情况下Majorana费米子可能是不稳定的, 会随着调制化学势强度的增大而消失.然而在某些特殊参数下, 调制强度无法改变Majorana费米子的存在性.与此同时, Cai等[38]讨论了非公度调制对拓扑相变的影响, 发现随着非公度调制强度的增加系统将经历从拓扑非平庸相向平庸的安德森局域相的转变.随后相当多的工作对调制的Kitaev链进行了深入的研究[39−41].本文将讨论(准)周期调制的p波超导量子线系统中的拓扑量子相变.

2 理论模型与方法

考虑一维具有(准)周期调制的p波超导量子线, 其哈密顿量可以写为

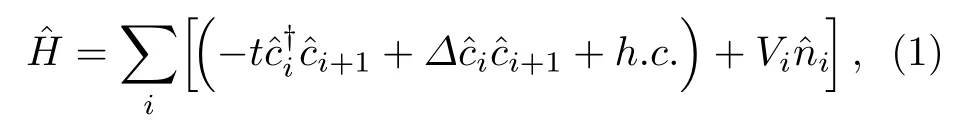
其中 V 是化学势的强度, δ 是任意的相移.α 控制系统的调制周期, 若 α =p/q 是有理数(p和q是互质的整数), 则 Vi是公度势; 若 α 是无理数, 系统则具有非公度调制.化学势是参数b的连续函数, 其中 b ∈[0,1).在没有超导配对的情况下, 即 ∆ =0 ,当 b =0 时, 若 α 为有理数, 系统处于拓扑非平庸相, 由非零整数的陈数所标记[42]; 若 α 为无理数,模型退化为著名的AA模型[43], 此时如果 V <2t ,系统中所有的单粒子本征态为扩展态并且具有非平庸的拓扑性质, 而当 V >2t 时, 所有的本征态都为局域态, V =2t 是扩展到局域相的转变点, 此时所有的本征态展现多分形的特性, 而这一系统中并不存在迁移率边[44]; 对于 b0 且 α 为无理数的情况[45], 系统具有能量依赖的自对偶特性, 其迁移率边可以解析地表示为 Ec=(2t−V)/b.对于存在超导配对的情况, 即 ∆0 , 若 α 为有理数, 模型哈密顿量为周期调制的p波超导量子线, 已经被广泛地研究[37], 文献[37]中指出此系统的拓扑相变依赖于相移 δ , 而在某些特殊 δ 点系统一直处于拓扑非平庸相不会受周期调制强度V所控制; 对于非公度调制, Cai等[38]指出随着非公调制强度的增大, 系统经历一个由拓扑非平庸相到安德森局域相的转变, 转变点在 Vc=2t+2∆ 处.由此可见, 在b=0的情况, 模型具有丰富的拓扑及局域化特性,已经引起了广泛的兴趣.在这篇文章中我们关注分别为有理数和无理数情况下系统的拓扑相变, 以及在 α 为无理数时系统的局域化特性.

通过 Bogoliubov-de Gennes (BdG)变换[46−48]把系统的哈密顿量(1)对角化, 定义一组准粒子算符:

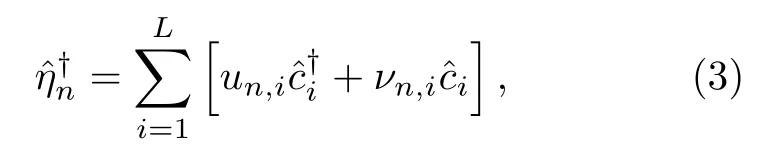
其中L是系统的格点数, n是能级指标且n=1,···,L.由于在哈密顿量(1)中所有的参数都选为实数, un,i和 νn,i也均为实数.哈密顿量可以用准粒子算符表示为其中En是准粒子的本征能量.由对角化关系得到下面的BdG耦合方程:

通过求解BdG方程, 可以得到准粒子的本征能量及其相应的本征波函数.由于BdG方程满足电子-空穴对称性, 即系统的能谱关于零点对称.系统的基态对应于所有负的准粒子的能级被填满的情况.在下面的分析中取 b =0.5.

3 结果分析与讨论

3.1 周期调制的p波超导线

这一小节讨论 α 为有理数情况下, 系统的拓扑相变.在开边界条件下, 我们通过数值求解BdG方程(4)得到准粒子的本征能量 En, 若系统处于拓扑非平庸相, 能谱中会出现零能的Majorana边缘态, 而当系统处于拓扑平庸相,Majorana零模将消失.图1计算了在 b =0.5 ,∆=0.2, V =1.5 和 δ =0 时, 能谱随参数 α 变化的情况, 即Hofstadter蝴蝶谱[49,50], 其中红色点表示非平庸的零模.随着 α 的增加, 系统表现出复杂的拓扑相变过程.作为具体的例子, 我们将分别讨论α=0, 1 /2 , 1 /3 的情况.

图1 Hofstadter蝴蝶谱: 随 α 变化的能谱, 红色点是零能 Majorana 费 米 子 b = 0.5, L = 120, ∆ =0.2 , V = 1.5,δ = 0Fig.1.Hofstadter butterfly: the energy spectrum varying with α.The red dotted point denotes the Majorana Fermion.b =0.5,L=120,∆=0.2,V=1.5 and δ =0.

在 α =0 时, 哈密顿量退化为标准的Kitaev模型[5], 系统在处经历一个拓扑相变, 在区域处于由 Majorana 零模所标记的拓扑非平庸相.可以看出当 δ 取 π /2 奇数倍时, 系统将一直处于拓扑非平庸相, 并不依赖于V的取值.

我们知道, 非平庸的Majorana零模可以由Z2拓 扑 不 变 量 来 表 征[5,37].对 于 α =1/2 和 1 /3 的 情况, 可以通过计算 Z2拓扑不变量, 解析地得到系统的相变点.考虑具有周期性边界的系统并对其进行傅里叶变换,其中,i=s+(l− 1)q,s=1,···,q表示一个超导元胞内的格点数, l =1,···,L/q 是第 l个超导元胞的位置, k 表示动量, 其取值范围为 [ 0 ,2π/q].哈密顿量(1)进行傅里叶变换之后可以写为

在动量空间下, 我们定义一组准粒子算符为[51]:它满足反对易关系:以及可 以 看 出 只 有和满足 Majorana费米子算符的定义, 即在新的算符基矢下, 可以把哈密顿量重新写成如下形式:

对于 s =1,···,q 时,

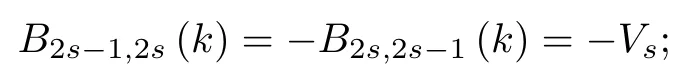
对于 s =1,···,q− 1 时,

对于 s =q , 有

B(k)是 一 个2 q ×2q 的 矩 阵 , 并 且 只 有B (0) 和B(π/q)是反对称矩阵.系统的 Z2拓扑不变量可以定义为[5,51]: M =sgn[Pf(B(0))]sgn[Pf(B(π/q))], 其中是反对称矩阵A的Pfaffian, P代表矩阵A中2N个元素的置换, s gn(P) 表示置换的符号.M =1 对应拓扑平庸相, M =−1 对应拓扑非平庸相, 而拓扑相边界可以由 M =0 来标记.当 α =1/2 时,

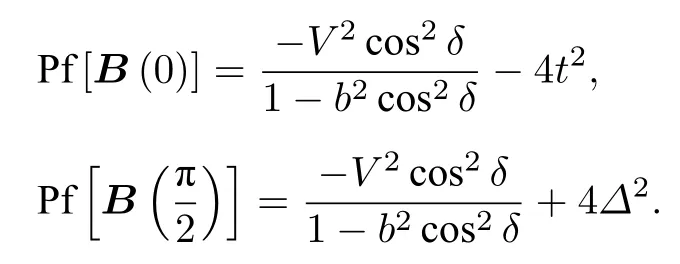
显 然 , P f[B(0)]<0 , 系 统 的 拓 扑 相 边 界 由得出, 即

图2(a) 展示了 b =0.5 , α =1/2 , δ =0 时, 系统拓扑相图.图中的黑色实线对应方程(7)所示的解析结果, 红色三角表示的是通过数值求解BdG方程(4)得到的相变点.可以看到数值结果与解析解得到的结果一致.在区域Ⅰ, 系统处于拓扑非平庸相,区域Ⅱ对应于系统处于拓扑平庸相.我们可以看到, 当 δ =0 时, 系统会经历拓扑非平庸相到拓扑平庸相的转变.由方程 (7) 可知, 当 δ 取值为 π /2 的奇数倍时, 任意小的 ∆ 将导致系统处于拓扑非平庸相, 而不依赖于周期调制的强度.图3(a)—图3(c)展示了 b =0.5 , α =1/2 , ∆ =0.2 , 不同 V 时, 能谱随着相移 δ 变化的情况.在V比较小的时候, 如图3(a)所示, V =0.2 , 在整个相移参数空间中,Majorana零模一直存在.随着V的增大, 能隙逐渐减小, 当它超过某个临界值时, 能隙将在某些 δ 的位置关闭, 随后再次打开, 而此时零模消失[图3(b),V=0.5], 对应于系统从拓扑非平庸相到拓扑平庸相的转变.然而当 V 足够大, 如图3(c), V =3 , 除了在 δ = π/2 和 3 π/2 处 Majorana 零模存在外, 几乎所有的 δ 区域都处于平庸相, 并且无论V值取多大, 这两点的零模始终存在, 这与我们的解析结果相一致.

图2 在 b =0.5 时, 参数 ∆−V 平面的拓扑相图 (a) α=1/2,L=120; (b) α =1/3,L=120 ; (c) α =(−1)/2 ,L = 2584Fig.2.Topological phase diagram in ∆−V plane with b=0.√5.(a) α =1/2,L=120 ; (b) α =1/3,L=120 ; (c)α=(−1)/2, L = 2584.

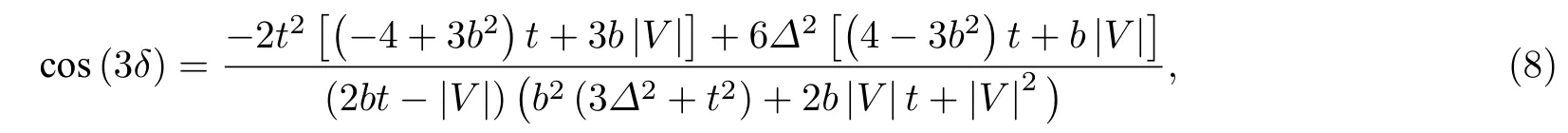
特别是, 当 b =0 时, 相边界可以写为一个简单的表达 式[37]: V3|cos3δ|=8t(t2+3∆2).在cos3δ=0时, 系统始终处于拓扑非平庸相, 并且不依赖于V 的取值.图2(b) 展示了 b =0.5 , α =1/3 和 δ=0时的拓扑相图.黑色实线为解析结果, 而红色三角为数值结果.由图可知, δ =0 时, 在某一特定的 ∆下, 随着周期调制强度V增强, 系统将出现一个拓扑相变.图3(d)—图3(f)分别展示了 b =0.5 ,α=1/3, ∆ =0.2 , V =0.2 , 2 和 6 时, 能量以相移δ为函数变化的情况.在小V情况, 系统在不同的δ参数下, 始终出现 Majorana零模[图3(d)], 而随着V的增加, 拓扑非平庸的区域逐渐减小[图3(e)],当调制强度足够大时, 拓扑非平庸区域完全消失,此时系统中并不存在某个特殊的 δ 使得Majorana零模一直存在 [图3(f)], 这与 b =0 的情况不符.我们可以看到, 图3(f)中虽然某些 δ 下最低能量接近于零, 但它并不是Majorana零模, 其准粒子的最低能量不低于 0.07.由此可见, 对于 b0 , α 为有理数的情况, 在某个固定的超导配对强度 ∆ 和调制强度V时, 系统的拓扑相变强烈地依赖于相移 δ.然而在某些 α 值下, 并不存在与 b =0 情况类似的特殊 δ 值, 使得拓扑相变不依赖于调制强度V.

3.2 准周期调制的p波超导线

图3 在开边界条件下, 本征能量随相移 δ 的变化.b =0.5 , ∆ =0.2 , L=2584Fig.3.Energy varying with phase shift δ with b =0.5 , ∆ =0.2 and L =2584 under open boundary condition.

为了得到图2(c)中所示的相图, 我们首先分别计算在开边界和周期边界条件下, 系统的准粒子最低激发能量, 如图4(a)所示.以 ∆ =0.2 为例,图4(a)展示了最低激发能量 E1随准周期调制强度V的变化.图中黑色实线表示周期性边界的情况, 黑色方块表示开边界的情况.当 V <1.5 时, 开边界条件下展示了零能, 而周期边界条件下存在有限的能隙, 这表明在开边界条件下系统中存在零模.在图4(b)和图4(c)中分别展示了在开边界条件下 V =1 时, 最低激发态的空间分布 ϕ1和 ψ1,这里此时最低激发态 ϕ1和 ψ1分别位于边界的左右两端,ϕ1和 ψ1的振幅不会重叠在一起, 而是分裂为两个在空间上独立的Majorana边缘态, 此时系统属于有 Majorana 零模的超导相.当 V ∈(1.5,2.5) 时, 开边界条件和周期边界条件下最低激发能量大于零,展示了相同的能隙, 并没有展示边缘态, 并且在开边界条件下最低激发态 ϕ1和 ψ1的振幅会重叠在一起, 且分布在整个空间, 此时系统属于超导相[如图4(b), 图4(c), V =2 ].当 V >2.5 时, 开边界和周期边界条件下, 能隙均消失, 其最低激发能量为零.以 V =3 为例, 其最低激发态 ϕ1和 ψ1局域在空间某一点上, 并不局域在边界位置, 表明此区域的零能态不是 Majorana零模 [如图4(b),图4(c),V=3].从准粒子的最低激发能量及其本征态的空间分布可以看出, 对于 α 为无理数的情况, 系统存在三种不同的相.

图4 (a)在开边界和周期性边界条件下最低激发态能量 E1 随准周期调制强度V的变化及其空间分布 ϕ1 (b)和 ψ1 (c), α=(−1)/2, b =0.5 , ∆ =0.2 , L=2584Fig.4.(a) The lowest excitation energies, E 1 , varying with the quasi-periodic mod√ulation amplitude, V, under OBC and PBC, respectively.The spatial distribution of the lowest excited state ϕ1 (b), ψ1 (c).α =(−1)/2 , b =0.5 , ∆ =0.2 , L =2584.

为了进一步确定系统中三种不同相的拓扑特性, 我们用 Z2拓扑不变量来表征其拓扑性质.在非公度势的情况下, 我们用散射矩阵 S 来计算 Z2拓扑不变量[52−54].散射矩阵 S 与在费米能级EF=0处的入射波和出射波的振幅有关,

这里, 2 × 2 的子块 R ,R′和 T ,T′分别为在超导线两端的反射和透射矩阵.Z2拓扑不变量定义为:M=sgn[Det(R)].只有当 M =−1 时, 在超导量子线两端才会出现非平庸的Majorana费米子.散射矩阵可以通过转移矩阵方法得到.基于哈密顿量(4), 零能的薛定谔方程给出:

这里 I 为 2 × 2 的单位阵.在这个基矢下, 透射和反射矩阵的关系为

拓扑不变量M就可以通过计算转移矩阵W得到.如图5(a) 所示, 我们计算了 b =0.5 , ∆ =0.2 时, 系统的拓扑不变量M随着调制强度V变化的情况.从图中可以看出, 当 V <1.5 时, M =−1 对应于由Majorana零模所标记的拓扑非平庸的超导相.而当 V >1.5 时, M =1 对应为拓扑平庸相.由此可以确定区域I为拓扑非平庸的超导相, 而在区域II和III中, 系统展现了拓扑平庸的特性.

区域II和III的最低激发态展现了不同的局域化特性, 通过计算逆参与率(inverse participation ratio, IPR)[57−61],区分系统最低激发态的局域和扩展性质.这里n是能级指标, un,j和 νn,j是 BdG方程 (4)的本征态,满足归一化条件,对于扩展态, IPR 的值以 1 /L 趋近零; 而对于局域态, 其IPR ∝ (1/L)0趋于一个有限值.图5(b)和图5(c)分 别 展 示 了 ∆ =0.2 , V =2 和 3 时 , 最 低 激 发 态IPR1随着系统尺寸的标度行为.V =3 时, 最低激发态 I PR1不随尺寸L的变化而变化, 在L趋近于无穷时, I PR1的值趋近于 0.45 , 表明此时其最低激发态为局域态.而对于 V =2 的情况, 最低激发态IPR1随着 1 /L 趋近于 0 , 展现扩展的特性.由此可知, 区域II为拓扑平庸的超导相, 而区域III对应为拓扑平庸的局域相.

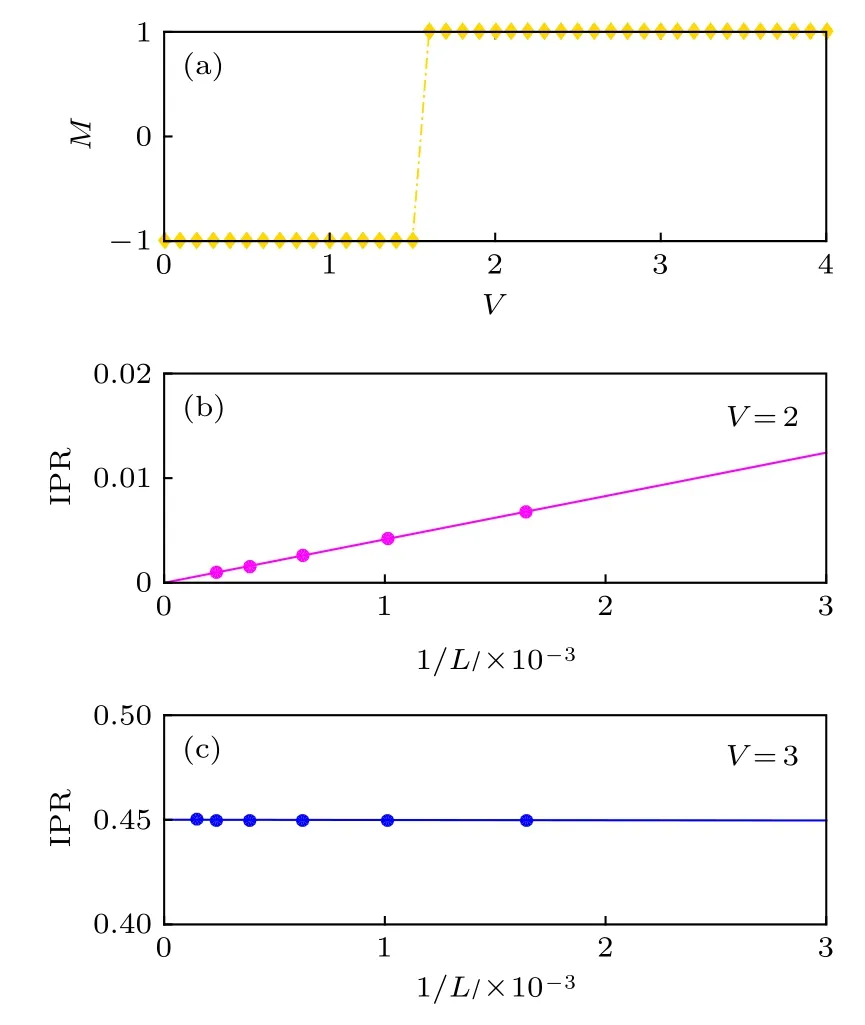
图5 (a) Z2 拓扑不变量随非公度势强度的变化; (b) V =2 时 I PR1 的 标 √度 分 析 ; (c) V =3 时 I PR1 的 标 度 分 析b=0.5, α =(−1)/2 , ∆ =0.2 , L=2584Fig.5.(a) Z2 topological invariant varying with the strength of the potential V; (b) the scaling of I P√R1 V =2 ;(c) the scaling of I PR1 V =3.Here, α =(−1)/2 ,b=0.5, ∆ =0.2 , L =2584.

图6 I PR 随准周期调制强度 V 和本征能量 En 的变化 α =(−1)/2 , b =0.5,L=144,δ=0 (a) ∆ =0 ; (b) ∆ =0.01 ; (c)∆=0.5; (d) ∆=0.8Fig.6.I PR varying with the amplitude of quasi-periodic modulation V and energy En.α =(−1)/2 , b =0.5,L=144 , δ=0: (a) ∆ =0 ; (b) ∆ =0.01 ; (c) ∆ =0.5 ; (d) ∆ =0.8.

当 ∆ =0 时, 系 统中存 在 迁移率 边[45], 其解析 表 达 式 为 Ec=(2t−V)/b.图6(a)展 示 了b =0.5,L=144,δ=0 和 ∆=0时不同能量 En的逆参与率随着调制强度V变化的情况, 其中蓝色实线表示迁移率边的解析解.随着p 波超导配对势的引入, 即 ∆0 , 系统中的迁移率边将如何改变? 首先考虑 ∆ →0 的情况.以∆=0.01为例[图6(b)], 可以看到原来能谱中间区域展现局域态特性的能态随着微小的超导配对项的引入开始变成扩展态, 而高能和低能部分并没有发 生 显 著 变 化.当 ∆ 为 有 限 大 时 , 如 图6(c)∆=0.5时, 可以看到高能部分的局域化特性并没有发生显著的变化, 中能部分局域化区域扩大, 而低能部分扩展区向局域化区域扩张.随着 ∆ 值的进一步增加, 高能和中能部分的局域化区域进一步扩大, 而低能部分的局域化区不断缩小[如图6(d),∆=0.8].由此可见, 由于超导配对项的引入, 迁移率边将无法用一个解析的形式表示.

4 结 论

本文研究了一维调制的p波超导体的拓扑量子相变.在公度势调制下, p波超导的拓扑性质强烈地依赖于 α 和 δ 的取值.当 b =0 时, 系统中存在特殊的相移 δ 使得Majorana零模的存在不依赖于公度势调制强度V.通过计算发现当 b0 时, 在公度势调制系统中, 存在特殊相移使得Majorana零模不受调制强度影响的结果并不是普适的.在非公度势调制下, 计算了相移δ=0时系统的低能激发谱、 Z2拓扑不变量以及逆参与率 (IPR)等, 发现当 p波配对强度0<∆<0.33时, 随着非公度势强度V的增加, 系统将经历从拓扑非平庸超导相到拓扑平庸超导相到拓扑平庸局域相的转变.而当 ∆ >0.33 时, 随着非公度势强度V的增加, 系统经历拓扑非平庸相到拓扑平庸局域相的转变, 这与 b =0 的结果一致.