交通发生吸引源集聚影响下路网宏观基本特性*

丁恒 周静文 郑小燕 柏海舰 张卫华

(合肥工业大学汽车与交通工程学院, 合肥 230009)

宏观基本图不受路网外部交通发生吸引源的影响, 描述了匀质性路网内累积车辆数与路网旅行完成率之间的关系, 可直观表达路网宏观基本特性.然而, 当路网内交通发生吸引源发生变化时, 会影响路网交通密度, 从而对宏观基本特性产生影响.为了分析交通发生吸引源不同集聚状态对宏观基本图的影响规律, 以交通发生吸引源发生吸引量和路段阻抗为参数, 建立交通发生吸引源聚集度模型.以方格式路网为分析对象,设计9组不同交通发生吸引源方案, 通过对比交通发生吸引源聚集度与路网宏观基本图曲线, 发现只有当路网处于拥挤流状态时, 交通发生吸引源聚集现象才会对宏观基本图产生影响, 并且路网中交通发生吸引源聚集度越低(交通发生吸引量分布越均衡), 路网旅行完成率就会越高.

1 引 言

宏观基本图(macroscopic fundamental diagram, MFD)描述了均质性区域路网内车辆密度 (veh·km–1)与空间平均流量 (veh·h–1)之间单峰低散射关系, 即该区域内累积车辆数 n (t) 与路网旅行完成率 G (n(t)) 之间的固有物理特性, 如图1(a)所示.在该特性中, 路网旅行完成率 G (n(t)) 随着累积车辆数 n (t) 变化而变化.当 n (t)ncr时, 路网旅行完成率 G (n(t)) 又随着累积车辆数 n (t) 增大而减小, 其中 ncr是临界累积车辆数.Gerolimins和 Daganzo[1]及 Gonzales等[2]根据路网宏观交通流的运行状态, 将MFD划分为自由流、临界流和拥挤流3种状态, 如图1(b)的Ⅰ、Ⅱ和Ⅲ.由于MFD可直观地描述区域路网的宏观交通状态, 简化了采用复杂OD数据对大规模交通网络建模过程, 被广泛应用于分析大范围交通网络.例如 Haddad、Yang、Ding和 Kim 等根据MFD描述的路网状态, 提出了单个区域[3−4]、两个区域[5−6]和多个区域[7−9]的边界限流控制方法, 有效地解决了大范围交通网络拥堵区交通控制问题.

MFD的概念由Godfrey[10]在1969年首次提出, 但限于当时的交通流检测手段, 其存在性并未得到验证.近些年随着数据采集及仿真手段的进步, 2008年Geroliminis和 Daganzo[1]根据日本横滨路网数据、Gonzales等[2]根据肯尼亚内罗毕路网数据验证了MFD的存在性, 此外Gao[11]运用斯德哥尔摩的交通数据发现了该城市路网也存在MFD.除了上述通过数据分析研究MFD存在外,也有部分学者通过解析模型分析MFD.如Leclercq等[12]利用变分法对不同路径上的MFD进行估计,然后将其聚合成一个统一的MFD, 进而确定与系统最优值相对应的MFD, 该方法对许多“非同质性”网络也适用; Daganzo等[13]利用旧金山路网数据提出了MFD的解析近似表达式; Courbon等[14]对比分析了获取MFD的3种方法: 分析法、基于路径的方法、检测器法, 并对该三种方法进行了仿真评价.

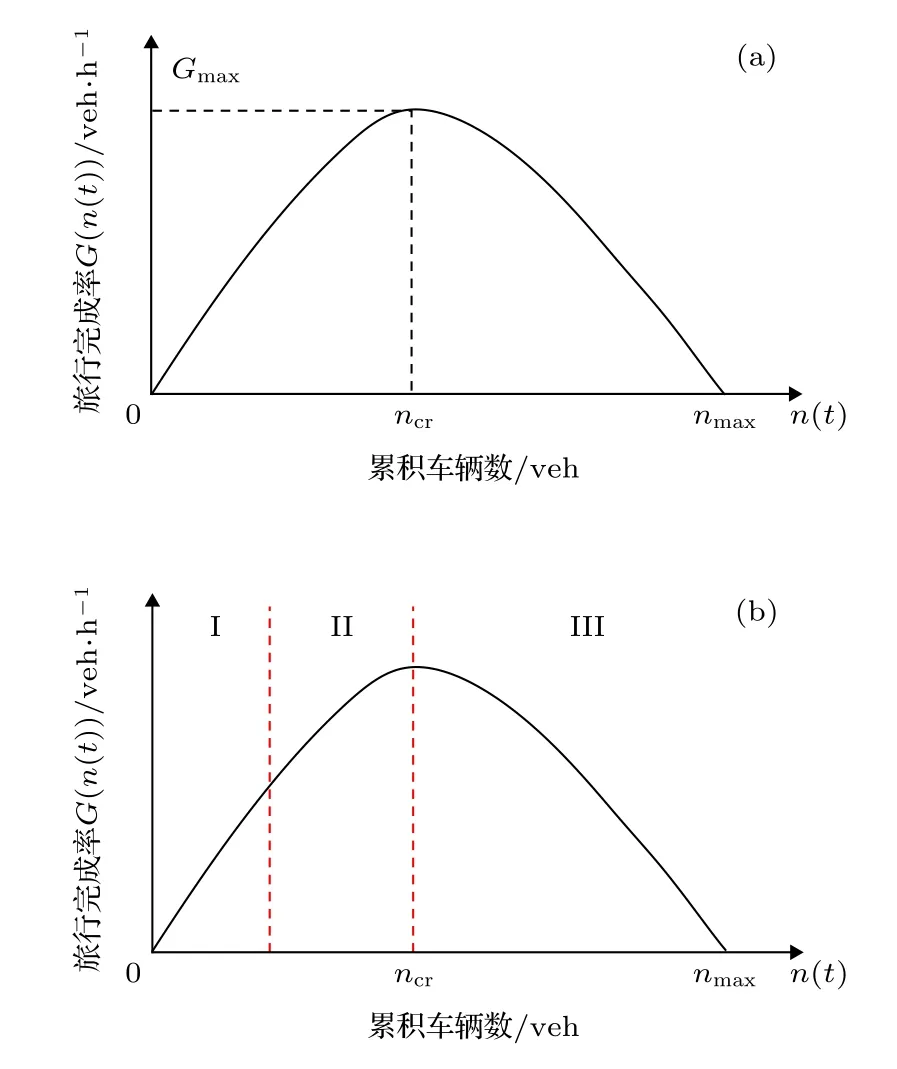
图1 MFD (a) MFD 的基本特征; (b) 路网状态划分Fig.1.MFD: (a) Basic characteristics of MFD; (b) state classification of MFD curve.

虽然MFD是特定路网的固有属性, 但其分布仍然受到路网一些特征参数的影响.相关学者对影响MFD因素的研究主要从交通条件、道路条件、管控条件以及选择行为4个方面进行.首先, 关于交通条件对MFD的影响[15−17], 典型的有Gayah和Daganzo[18]提出交通拥堵分布不均匀会导致MFD的“滞回现象”; 许菲菲等[19]采用不同的交通管控措施, 得出交通需求的剧烈变化、公交专用道的设置、车道禁行都会不同程度的影响MFD; 朱琳等[20]通过对比分析路网平均流量-平均密度关系的时段分布差异, 证明了交通密度分布的不均衡性是影响路网宏观交通状态的根本因素; Geroliminis和Sun[21]提出路网中车辆密度的空间分布是影响MFD散射特性及其形状的关键因素之一; Geroliminis等[22]发现交叉口处左转交通流的存在降低了MFD的最大值.其次道路条件对MFD的影响研究, 如Buisson等[23]分析了城市路网、穿越城市的高速路网与环城高速路网对MFD的影响, 并认为高速网络不存在MFD, 并且外部OD需求对MFD是没有影响的.再次, 不同的交通管控条件也会影响MFD, 其中管控措施和参数的研究受到重点关注.Jin等[24]通过元胞传输模型发现在自由流状态下, MFD比较稳定, 而间断流状态下信号控制使得网络交通流不稳定, 进而影响 MFD形状;Alonso等[25]基于真实数据的统计分析, 得出交通管制影响链路和路网级别的交通流变化.最后, 针对出行者不同的选择行为, Leclercq和Geroliminis[26]通过研究局部非均质性交通流对MFD形状的影响, 可知路径选择和异构的局部交通容量可能会导致交通拥堵的时空分布不一致, 进而影响路网MFD的形状和分布; Mazloumian等[27]基于对MFD空间分布不均匀的研究, 可知路径选择和交通需求是影响MFD散射的重要因素.总体而言,不同的影响因素归根结底都是影响路网密度, 进而对MFD产生影响.在交通发生吸引源分析方面,虽然Buisson等[23]证明了外部OD需求对区域路网的MFD是没有影响的, 但并没有说明路网内部的交通发生吸引源分布是否对MFD产生影响.而实际上, 路网内交通发生吸引源分布不均匀时, 其产生的交通量会改变局部路网的交通密度, 进而可能影响MFD分布.

为了分析交通发生吸引源对路网MFD产生的影响规律, 本文主要开展以下两个方面工作:1)根据区域路网内交通发生吸引源的时空分布,以交通发生吸引源发生吸引量和路段阻抗为动态参数, 提出交通发生吸引源聚集度分析模型; 2)以4 × 4方格网状的区域路网为研究对象, 根据不同发生吸引源的分布, 通过数据验证不同聚集度条件下交通发生吸引源对MFD的影响规律.

2 交通发生吸引源聚集度模型

聚集度的概念在经济学和地理学等领域中应用比较广泛, 一般用来形容某个区域内某个经济产业或某个地理指标的聚集程度.与产业在空间和发生吸引强度上分布类似, 路网中交通发生吸引源也存在着一定的聚集形态.因此将聚集度概念引入交通领域, 用来描述交通发生吸引源的集聚状态.然而, 与产业分布不同在于, 路网中各个路段的阻抗是实时变化的, 因此交通发生吸引源聚集程度也变化的较为频繁.因此, 在分析交通发生吸引源聚集形态时, 必须考虑到时间因素.

假设路网内有N个交通发生吸引源, 路网可划分为M个区域.根据发生吸引源数量、发生吸引量规模、路网容量, 建立交通发生吸引源聚集度评估模型, 步骤如下:

首先, 根据N个交通发生吸引源空间位置坐标, 通过M个区域划分对交通发生吸引源进行分类.分类方法是根据路段密度和路段速度, 通过路网交通状态识别[28]获得交通发生吸引源影响下的路段交通状态, 分为非常畅通、畅通、轻度拥堵、中度拥堵以及严重拥堵5种状态等级, 通过最小生成树法初始划分、归一化割法深度划分以及反向动态合并的过程得到对交通发生吸引源分类的M个区域[29].

其次, 计算交通发生吸引源空间分布基尼系数:

式中, Pi表示划分的M个区域中第i个区域交通发生吸引源容量(停车需求)占整个路网所有发生吸引源容量(停车需求)的比重, xi表示第i个区域路网交通容量占整个路网交通容量的比重.基尼系数 G =0 时, 表明停车需求在空间分布是均匀的,G越大(最大值为1), 表明停车需求在空间分布越不均匀.

再次, 采用 Ellision和 Glaeser[30]提出的 EG集聚指数来测定交通发生吸引源聚集度指数, 即评估模型为

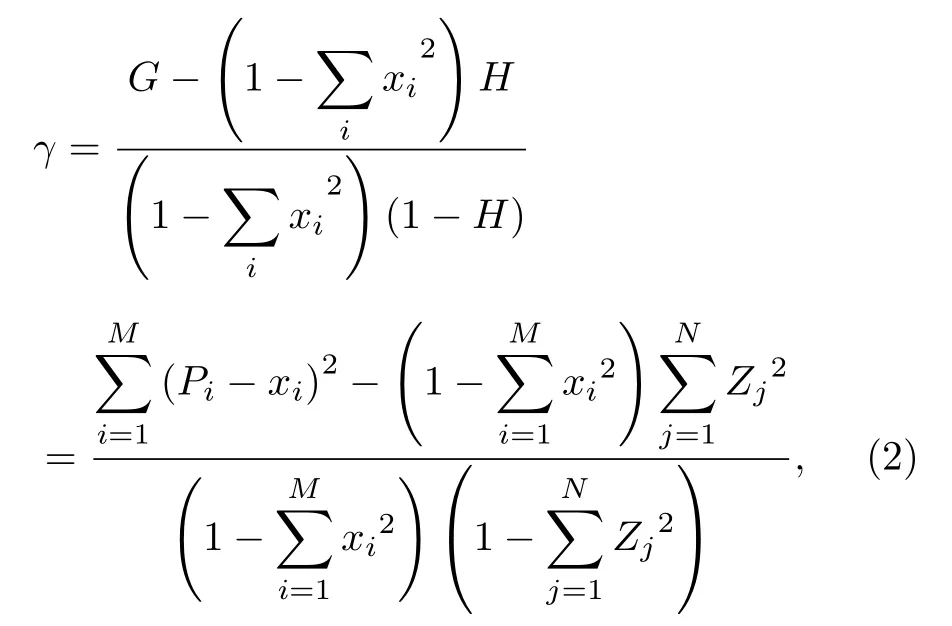
式中: γ 为交通发生吸引源聚集度指数; H为赫芬达尔指数,表示 N 个交通吸引源中第j个区域交通发生吸引源总容量(停车需求)占整个路网所有发生吸引源容量(停车需求)的比重.

考虑到交通流的动态变化, (2)式中的空间分布基尼系数G以及赫芬达尔指数H也会随着路网交通状态即路网交通阻抗的变化而变化.交通越拥堵的地方, 交通发生吸引强度越大.为了更好地描述路网聚集状态, 假设交通发生吸引源的聚集状态与道路交通阻抗呈正相关, 即交通发生吸引源配置越聚集, 道路交通阻抗越大, 且道路交通阻抗在聚集度模型中属于正向因子, 则考虑交通阻抗的集聚度评估改进模型为

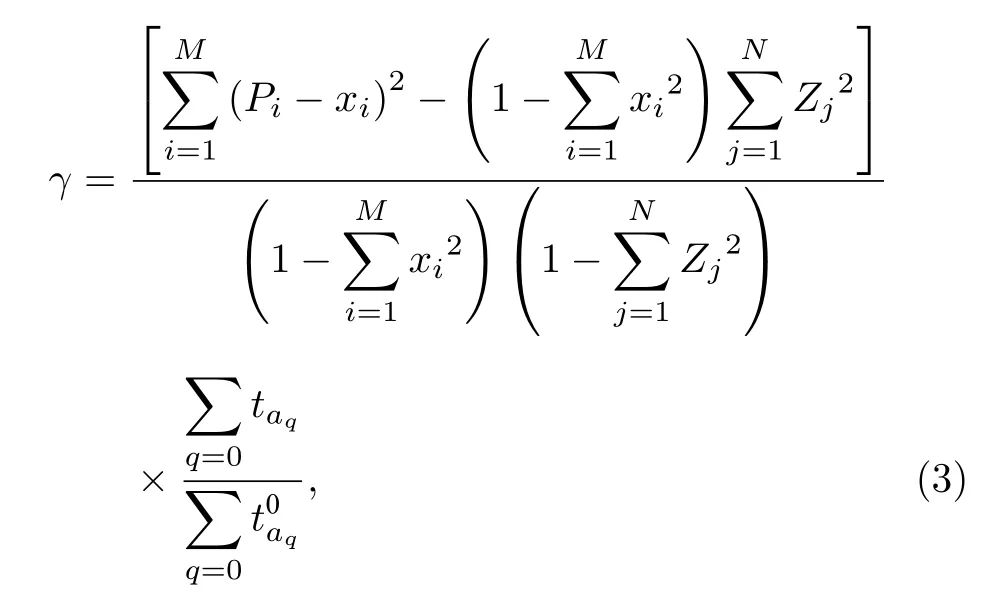
考虑路网实时状态, (3)式中引入了路网交通阻抗 ta, 其计算需要考虑路段不同交通参数.根据四兵锋等[31]提出的道路阻抗模型, 建立考虑多种路面的道路阻抗函数模型:

3 聚集度指数计算过程

为满足实际交通管控的需要, 在交通发生吸引源聚集度模型基础上, 计算路网交通发生吸引源聚集指数, 并以此分析路网交通发生吸引源的动态集聚状态.步骤如下:

Step1选择一个路网, 确定路网内交通发生吸引源的分布、规模.

Step2划分子区.在保证空间连续和子区内密度异质性最小化的前提下, 根据交通流数据, 然后考虑区域路网内的交通发生吸引源、交通拥堵状态以及交通流大小等因素将分布不均匀的区域路网划分为几个密度均匀的子区.

Step3计算路段交通阻抗.路段阻抗与断面形式有关.路段的阻抗函数的计算步骤基本类似,由于单幅路面的阻抗函数最复杂, 本文以单幅路为例给出段阻抗函数计算步骤如下:

首先, 由(4)式道路交通阻抗模型的定义, 需要确定路段零流量条件下的阻抗.根据1976年Branston[32]路段阻抗函数的理论特性: 1)当流量充分小时, 路段阻抗接近于“零流”阻抗; 2)在流量远小于道路通行能力时, 路段阻抗随流量变化而缓慢变化; 3)在“稳态”系统状态下, 阻抗函数曲线变成饱和流量纵坐标的渐近线.可以通过交通调查或者仿真的手段获得不同路段上一般机动车的平均零流阻抗.

然后, 标定参数.对于单幅路面的路段, 假定共观测到Z组样本值, 其中第k组样本值为以及 Ca, Ca,是确定的.为便于描述作如下变换:

确定α1,α2,α3,α4,β1,β2,β3,β4参数, 满足:

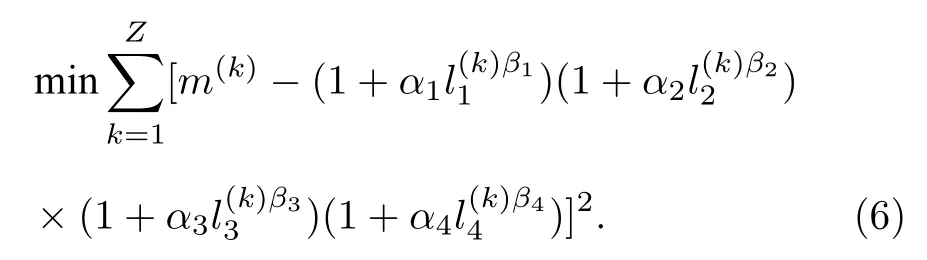
根据一阶极值条件可得关于参数a1, a2, a3,a4, b1, b2, b3, b4的非线性方程组.按照常规的方法求解非线性方程组的解析解难度较大, 本文采用Broyden求解方法[33].为了降低求解误差的影响, 提高参数数值解的准确性, 设置求解精度为10–8, 可得满足精度要求的参数数值解.由于该非线性方程组存在多组解, 所以在计算迭代时, 对初始迭代值的选取有一定要求.因此,

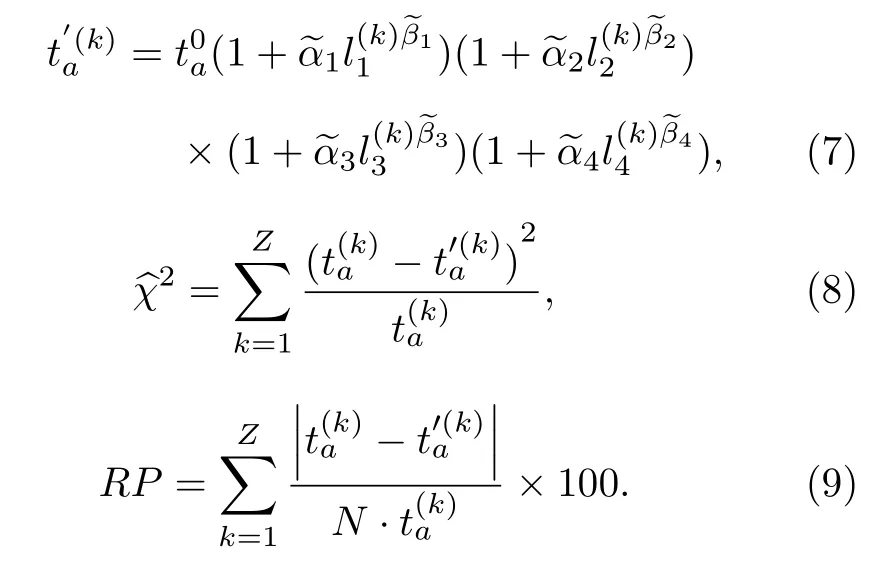
最后, 获得每条路段的交通阻抗, 进而得到路网整体交通阻抗.

Step4由Step2获得各子区的交通发生吸引源的相关信息, 然后根据(1)式计算得到空间分布基尼系数G, 并计算赫芬达尔指数H, 将Step3得到的路网交通阻抗带入(3)式, 进而可以获得实时的路网交通发生吸引源的聚集度指数.

Step5结束.

4 交通发生吸引源聚集效应对路网MFD的影响分析

根据Gerolimins等[1]的研究结果, 存在理想MFD的子区范围一般在4—8 km2.在该区域范围内, 路网结构较为单一, 一般接近于方格网状路网.因此, 为了分析交通发生吸引源聚集度指数变化对路网宏观基本特性的影响, 本文采用4 × 4方格形路网进行交通仿真, 如图2.该路网有16个交叉口, 96 条路段, 且每条路段均为三车道.将该路网外围的16个路口作为路网背景交通量输入点, 然后在路网内部设置8个车流输入点作为交通发生吸引源, 每 300 s 采集交通流数据一次, 并得到路网MFD数据以及相应的聚集度指数.

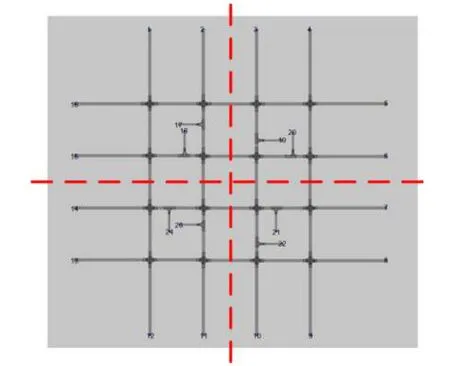
图2 仿真路网Fig.2.Simulation road network.

4.1 交通发生吸引源聚集效应对路网密度影响分析

路网内交通发生吸引源的聚集状态一定程度上可以由路网中交通密度分布状态体现.在上述路网中设置不同配置的交通发生吸引源, 如表1所示, 在相同的背景交通流的影响下获得某一个信号周期(150 s)内的路网交通密度分布, 如图3所示.

图3中 (a1)、(a2)、(a3)、(a4)和 (a5)是相同的, 均表示在未加载交通发生吸引源情况下路网交通密度分布.图3中 (b1)、(b2)、(b3)、(b4)和(b5)分别表示5种总规模相同但分布不同的交通发生吸引源配置情况.图3 中 (c1)、(c2)、(c3)、(c4)和(c5)分别表示在路网背景交通密度和不同配置的交通发生吸引源条件联合影响下, 某一个信号周期(150 s)内发生吸引交通量影响下路网交通密度分布.可以发现, 在未加载交通发生吸引源的情况下, 路网交通密度分布是比较均匀的, 最大的单车道交通密度大约是 5 pcu·km–1; 当路网中加载交通发生吸引源之后, 路网交通密度分布明显发生变化, 并且局部最大单车道交通密度达到134.7 pcu·km–1, 远超过 5 pcu·km–1, 并且交通密度较大的路段都是与交通发生吸引源相连或邻近的路段.因此, 交通发生吸引源的聚集效应会改变路网交通密度的分布.

表1 交通发生吸引源配置参数Table 1.Traffic generation and attraction source configuration parameters.

4.2 交通发生吸引源聚集效应对路网MFD动态影响分析

4.2.1 参数标定

由4.1节可知, 交通发生吸引源的聚集效应会影响路网交通密度的分布, 所以进而会影响路网MFD的基本特性.根据(3)式, 在不同的交通发生吸引源分布条件下, 分析路网内交通发生吸引源的聚集状态对路网MFD的动态影响.将路网内的8个交通发生吸引源的总规模分别设置为800,1200, 2000 pcu·h–13 种情况, 获得路网累积车辆数(n)与路网旅行完成率(G)之间的关系, 即路网MFD, 如图4所示.

根据 Gonzales和 Chavis[34]的研究发现, 尽管MFD的形状依赖于OD需求, 然而此关系并不随时间变化, 在一定交通范围内可以采用如G(n(t))=a ·(n(t))3+b·(n(t))2+c·n(t)+d的3次方程式近似表示.由实验数据可得, 路网MFD拟合曲线参数标定如表2所示.

根据不同交通发生吸引源条件下MFD数据在Ⅰ、Ⅱ和Ⅲ 3种状态分布可知, 在Ⅰ、Ⅱ状态,MFD 并没有明显的波动; 在状态Ⅲ, 800 pcu·h–1和 1200 pcu·h–1两组数据的 MFD 有明显的较大波动, 而 2000 pcu·h–1组仿真得到的 MFD 波动幅度较小.因此, 一定程度上路网宏观基本图会受到交通发生吸引源的影响.

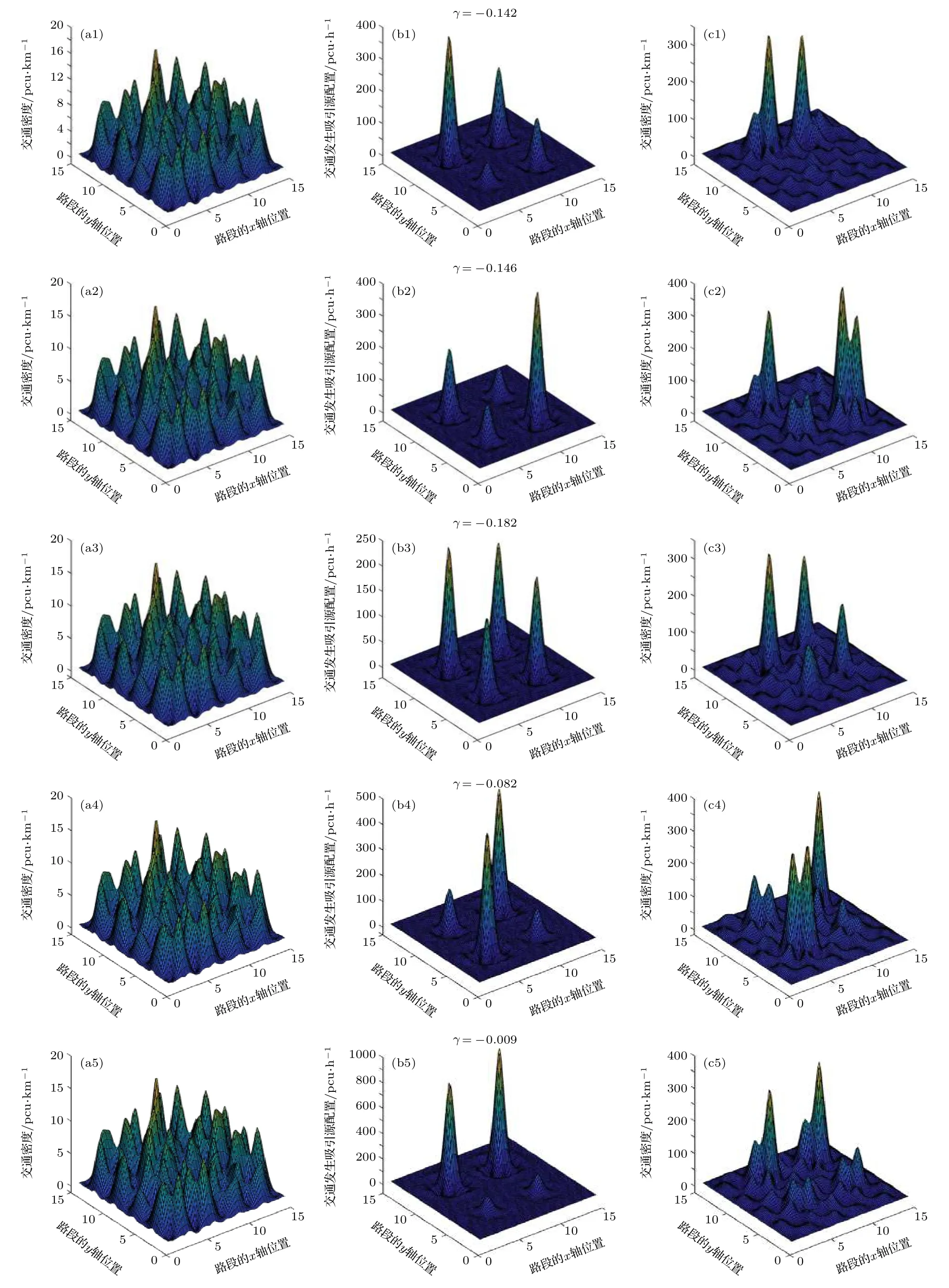
图3 不同交通发生吸引源集聚影响下交通密度分布Fig.3.Traffic density distribution under different traffic generation and attraction sources.

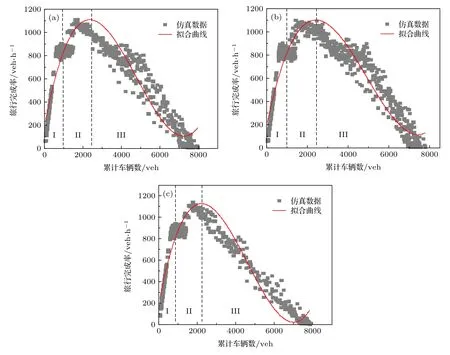
图4 不同交通发生吸引源规模下路网 MFDs (a) 800 pcu·h–1; (b) 1200 pcu·h–1; (c) 2000 pcu·h–1Fig.4.MFDs under different traffic generation and attraction source scale: (a) 800 pcu·h–1; (b) 1200 pcu·h–1; (c) 2000 pcu·h–1.

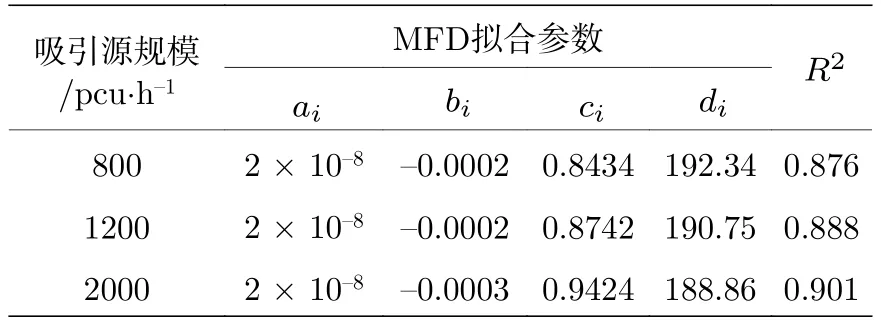
表2 不同交通发生吸引源规模下MFD参数Table 2.MFD parameters under different traffic generation and attraction sourcescale.

4.2.2 动态分析

为了进一步研究交通发生吸引源聚集度模型与路网宏观基本图波动的动态关系, 通过动态加载交通流量, 并且每 300 s采集交通流数据一次, 开展实验分析.

在初始状态, 路网交通流为自由流, 路网交通阻抗可认为零流阻抗.再由聚集度模型的定义, 将路网划分为4个子区, 每个子区包含2个交通发生吸引源, 如图2所示.设计的9组仿真实验按照交通发生吸引源总规模分为3大组, 分别为A组、B组和C组, 每大组包含三个实验方案, 然后依据交通发生吸引源集聚度模型计算9组仿真实验的初始聚集度指数, 且每大组的3个实验方案的初始聚集度指数依次递减, 如表3所示.3大组实验的MFD及动态聚集度指数曲线如图5所示.

根据路网的聚集度曲线的变化趋势可知, 随着路网密度的变化, 聚集度曲线有明显的3个变化阶段, 如图5所示.参考图1(b)中MFD的状态划分可知, 聚集度曲线在状态Ⅰ时基本没有变化, 在状态Ⅱ时开始有小幅的变化, 在状态Ⅲ时开始急剧变化并逐步平稳(路网全部阻塞).

为了更好地对比分析交通发生吸引源不同集聚影响下的MFD波动特性, 将上述9组仿真实验MFD数据进行三次多项式拟合, 相关参数标定如表4所示.从A组、B组和C组仿真实验中每一份实验数据的拟合效果来看, R2值都大于0.9, 表明每份数据的拟合效果都比较好.

A组、B组和C组的MFD拟合曲线与相应的聚集度曲线如图5所示.仿真实验中基本参数都保持一致, 交通发生吸引源相同规模下不同分布是唯一变量, 即交通发生吸引源不同的聚集度是唯一变量.因此, 路网MFD的变化就是由交通发生吸引源的聚集效应导致的, 而交通发生吸引源聚集度体现了交通发生吸引源的聚集效应, 且仿真过程中每300 s采集一次路网数据, 可获得相应的MFD数据点以及聚集度指数, 则保证了MFD曲线与聚集度曲线基本实时对应.

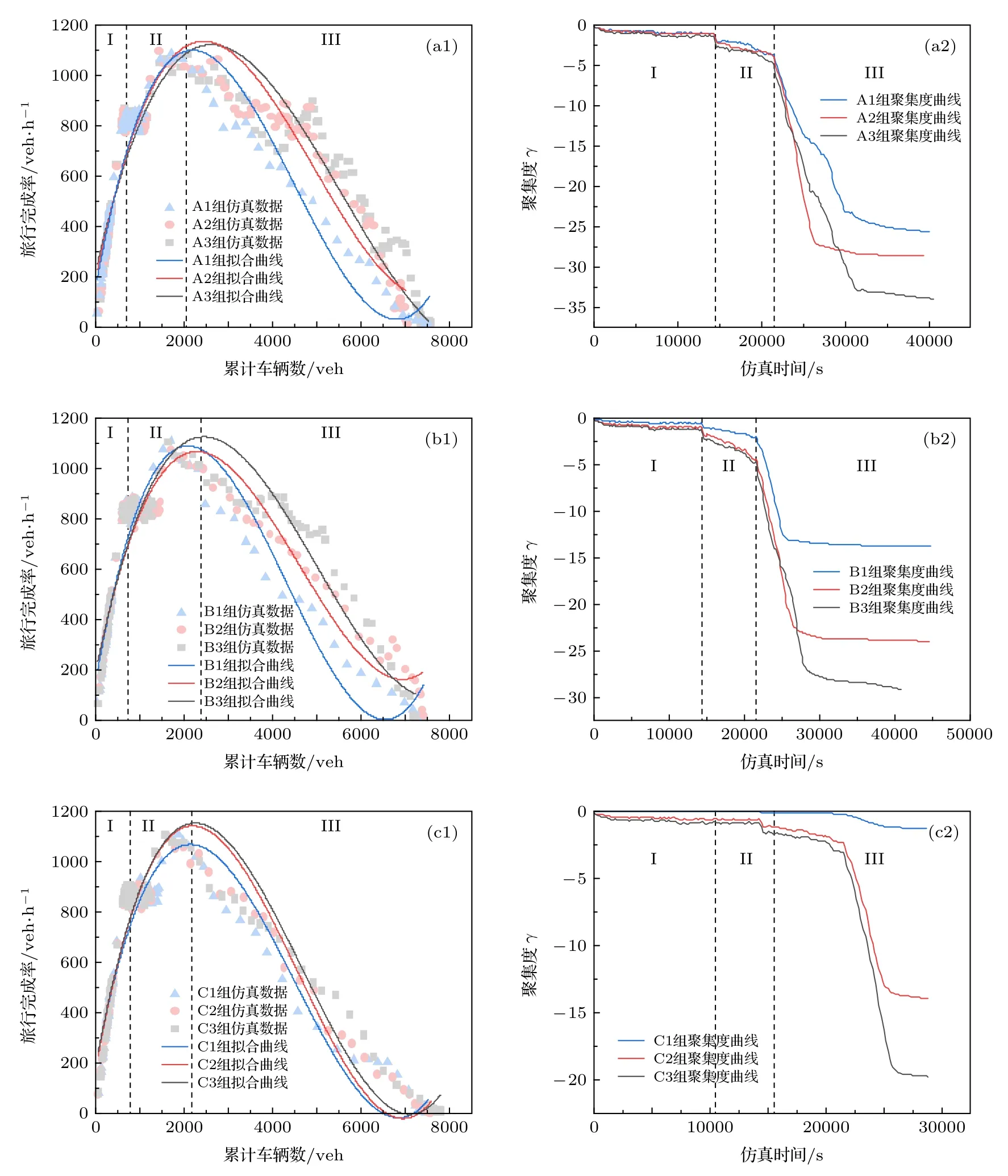
图5 不同交通发生吸引源配置条件下MFDs和聚集度曲线 (a1) A组仿真实验MFD; (a2) A组仿真实验聚集度曲线;(b1) B 组仿真实验 MFD; (b2) B 组仿真实验聚集度曲线; (c1) C 组仿真实验 MFD; (c2) C 组仿真实验聚集度曲线Fig.5.MFDs and aggregation degree curves under different traffic generation and attraction source configuration: (a1) MFDof group A simulation scheme; (a2) aggregation degree curve of group A simulation scheme; (b1) MFDof group B simulation scheme;(b2) aggregation degree curve of group B simulation scheme; (b1) MFDof group C simulation scheme; (b2) aggregation degree curve of group C simulation scheme.

综合图5和表5可知, 在状态Ⅰ时, 路网累积车辆数在0—600 veh之间, A3组平均旅行完成率相比 A1组增加了 0.77%, 相比于 A2组增加了0.61%, A2组平均旅行完成率相比A1组增加了0.16%, A组、B组和C组仿真实验的MFD拟合曲线都几乎重叠, 没有明显差异, 说明交通发生吸引源的集聚效应对此状态下的MFD几乎没有影响; 在状态Ⅱ时, 路网累积车辆数在 600—2000 veh之间, A组、B组和C组仿真实验的MFD拟合曲线产生一定的差异, A3组平均旅行完成率相比A1组增加了3.13%, 相比于A2组增加了1.14%,A2组平均旅行完成率相比A1组增加了1.96%,说明交通发生吸引源的集聚效应对此状态下的MFD 已经产生影响, 但影响有限; 在状态Ⅲ时, 路网累积车辆数在2000—8000 veh之间, A3组平均旅行完成率相比A1组增加了30.96%, 相比于A2组增加了3.29%, A2组平均旅行完成率相比A1组增加了26.79%, 不同交通发生吸引源条件下MFD拟合曲线之间有明显的差异, 且A1组MFD拟合曲线偏低、A2组MFD拟合曲线居中、A3组MFD拟合曲线偏高, 对应状态Ⅲ的聚集度曲线可知, A1组聚集度曲线值最大、A2组聚集度曲线值相对次之、A3组聚集度曲线值最小.由表5可知, B组、C组结果类似, 说明交通发生吸引源的集聚效应对状态Ⅲ下的MFD影响较大, 且交通发生吸引源聚集度指数越小, 路网旅行完成率越高, MFD波动值越高.

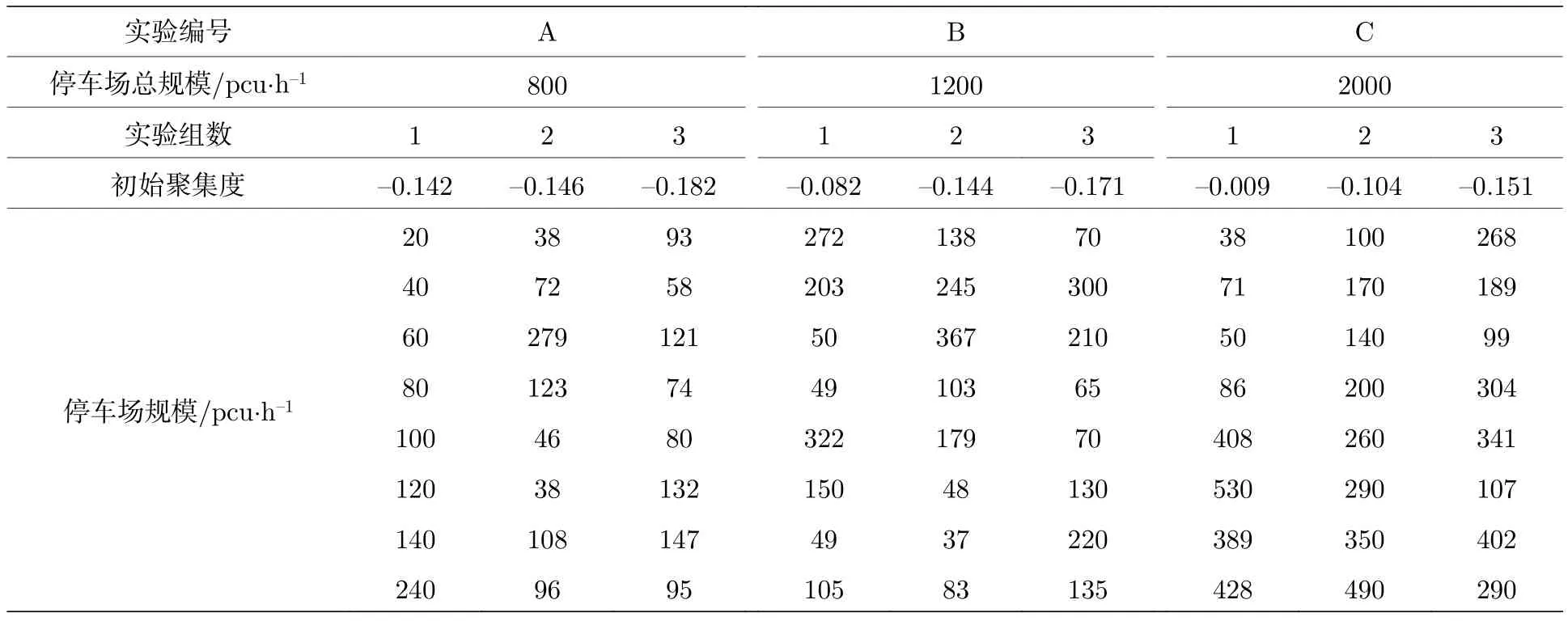
表3 仿真实验基本参数Table 3.Basic parameters of simulation experiment.

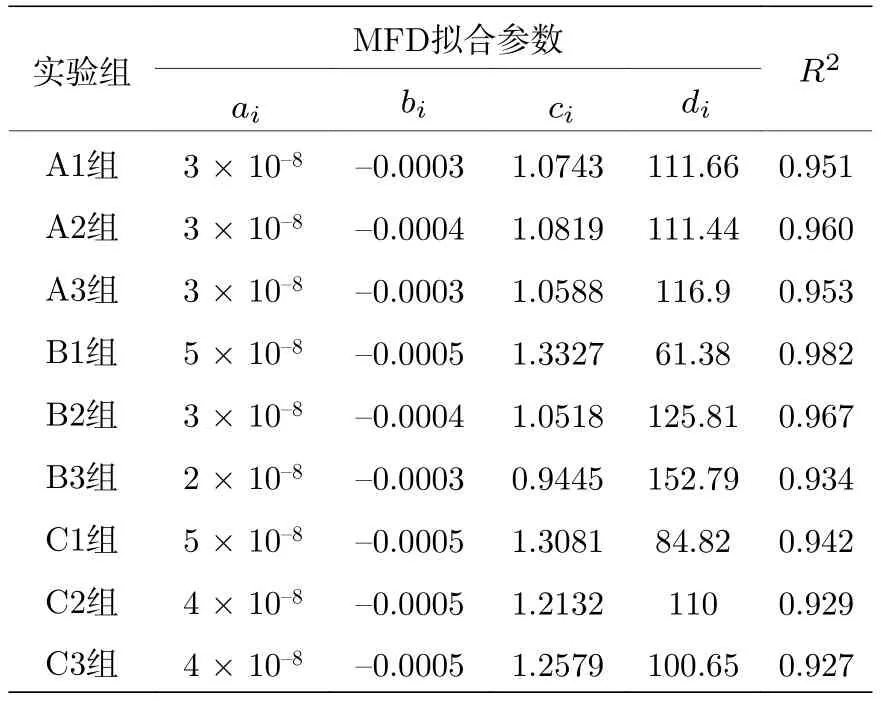
表4 不同交通发生吸引源配置条件下MFD参数Table 4.MFD parameters under differenttraffic generation and attraction sourceconfiguration.

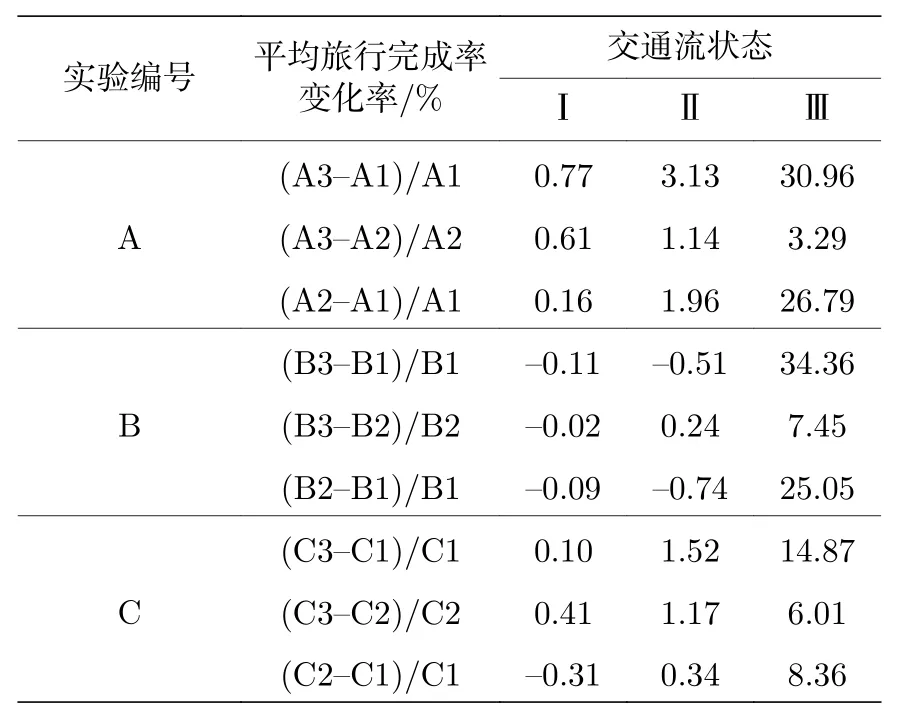
表5 各组仿真实验平均旅行完成率评估参数Table 5.Evaluation parameters of the average trip completionflow of simulation experiment.

5 结 论

本文在MFD波动特性的基础上, 从交通发生吸引源集聚现象出发, 提出了一种考虑交通阻抗的交通发生吸引源聚集度模型; 并以9组仿真实验为例, 获得路网在不同交通发生吸引源聚集状态下的MFD和聚集度曲线变化特征.对比不同交通发生吸引源条件下MFD变化规律, 有以下结论:

1)当路网交通流处于自由流状态时, 路网交通发生吸引源集聚不会对MFD产生影响; 在临界流状态时, 交通发生吸引源集聚对MFD有一定的影响; 当路网处于拥挤流状态时, 交通发生吸引源集聚对MFD有显著的影响.

2)在相同的路网流量条件下, 当路网处于拥挤流状态时, 交通发生吸引源聚集状态越均衡, 即聚集度指数越小, 路网旅行完成率越高(MFD曲线向上波动).

3)交通发生吸引源聚集度指数随着路网内交通发生吸引源的配置以及路网交通流的变化而变化; 在路网交通发生吸引源配置不变的情况下, 路网交通发生吸引源聚集度指数在自由流状态下没有较大的变化, 在临界流状态下开始有一定的变化, 在拥挤流状态下开始急剧下降并逐步平稳.

通过本文的研究, 建立了路网交通发生吸引源与MFD变化之间的宏观动态变化关系.依据该关系, 可通过调节路网内各个停车场交通发生吸引强度, 改变路网交通发生吸引源聚集度指数提高路网旅行完成率, 从而提高路网运行效率, 为城市路网内大型交通发生吸引源(停车场、医院、学校、商场等)的配置, 以及交通管控(停车收费、路段管制、信号灯控制等)提供一定的理论支持.由于本文是在一个规则的方格形路网分析交通发生吸引源聚集规律的, 而实际路网是比较复杂的.实际路网特征的相关MFD特性还有待进一步研究.