标准船模的CFD多维度仿真与拖曳水池试验对比

(上海船舶运输科学研究所 航运技术与安全国家重点实验室，上海 200135)

船舶设计过程中，需要对船舶的性能进行评估，计算流体力学仿真(CFD)和拖曳水池船模试验是研究船舶性能的重要手段。CFD方法虽然是高效的，但是不可避免的，其计算效率和精度受到使用人员的经验、计算模型设置等因素的影响，局部细节需要特殊处理，甚至在某些情况下出现较大误差。

通常而言，在船模拖曳水池进行试验的时候，由于试验条件、时间和成本的限制，都是将单次试验结果作为最终结果。事实上，根据ITTC规范中对于试验流程和对试验不确定度分析的建议，单航次试验结果都是在围绕着试验真值一定范围内波动，有相应的不确定度水平。

大部分研究中，都是将单航次船模试验结果作为验证标准，CFD作为仿真手段，通过计算模型的调整，寻找出尽可能贴近试验结果的策略，因此，对船舶性能进行评估的时候，需要面对船模试验结果的一定范围内的不确定性及CFD方法出现较大误差的可能性。为此，对一艘标准船模开展三部分工作：①进行船模拖曳水池的重复性阻力试验；②基于与试验一致的边界条件，通过设立不同的计算模型，进行CFD多层次仿真；③对比以上结果，并提出改善精度的措施。船模主尺度见表1。

表1 船模主尺度

1 理论分析

1.1 计算方法

目前工程上最常用的仍然是RANS方法，其中最常用的是二方程模型，k-ε模型、k-ω模型，SST模型等。计算工具采用STAR-CCM+软件。本文将速度进口、压力出口、自由液面、船体壁面等作为边界条件。

网格划分方法和网格密度对计算结果有明显影响。离散格式主要对计算效率造成影响，对结果的精度的影响十分有限。

在近壁面处的流动，由于是从粘性底层到湍流的转化，需要壁面函数处理。RANS方法通过壁面函数控制近壁面处流动问题，通过壁面函数结合湍流模型求解计算域。通过引入无量纲数值Y+进行控制。

时间步长Δti按照库朗数进行控制。当库朗数小于推荐值之后，计算结果受时间步长的影响可近似消除。本文按照以下公式计算。

(1)

式中:Δxi为网格尺寸;C为推荐库朗数。

通过以上分析，影响计算的因素包含湍流模型的选择、网格划分方法、离散方程的选择、边界层处理以及时间步长的设置等，以上各因素的叠加最终对结果造成影响。在实际计算过程中，离散方程主要对计算效率产生影响，时间步长按照库朗数相对恒定的原则，认为不会对结果产生影响。船模阻力仿真结果主要受网格密度、近壁面处理、湍流模型的影响[1-2]，因此,着重考虑这3个因素。

1.2 计算模型

1)计算域设置。在船艏、船舯和船艉区域进行加密，自由面处进行加密，见图1。

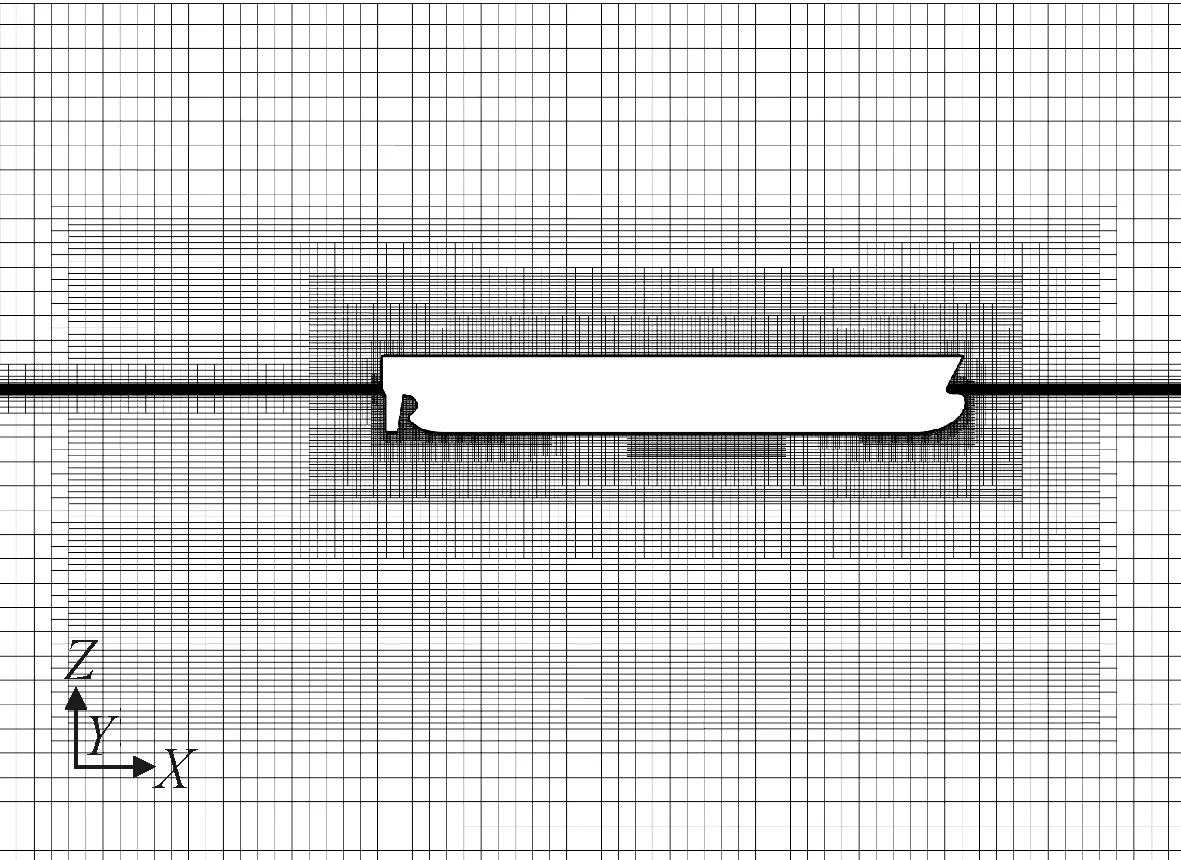
图1 计算域

2)网格设置。选择3种网格密度，网格增长率按照ITTC推荐的，在半个计算域内网格总量分别为60万、114万、233万。

3)Y+设置。近壁面处第一层网格的高度用Y+进行无量纲表示。求解RANS方程时，通常将Y+设置在60～300之间，本文将Y+设置为60、120、240。

4)湍流模型设置。考虑实际操作过程中的适用性，选取标准k-ε，k-ω模型以及SST模型为目标湍流模型。

汇总形成计算矩阵见表2，计算量共计27次。

表2 计算矩阵

2 拖曳水池阻力试验

依照ITTC规范对于船模试验的推荐流程，将目标船型按照与CFD计算的一致比例加工成船模，并保证船模精度满足ITTC要求；用于船模试验的仪器均经过校准和检验，能够保证精度在可控范围内。

试验在上海船舶运输科学研究所的船模拖曳水池进行，水池长192 m，宽10 m，水深4.2 m。阻力试验流程及布置示意见图2、3。

图2 阻力试验流程

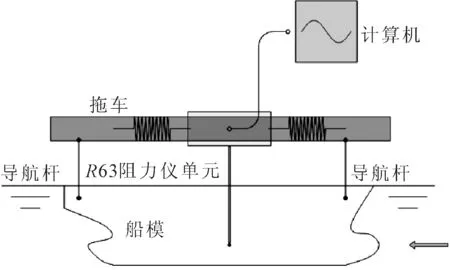
图3 阻力试验示意

通过复合航次试验降低试验的随机误差。采用不确定度的方式，计入试验的随机误差和各类仪器设备的系统误差。关于不确定度的计算，参照ITTC相关规程[3-5]。通过计入船模试验流程中各项仪器设备和试验随机误差对阻力试验结果的影响，本试验在95%置信区间(K=2)时扩展不确定度为

4.646×(1±0.32%)

(3)

图4 船模试验规程示意

3 计算结果与对比分析

CFD仿真结果波形图见图5。

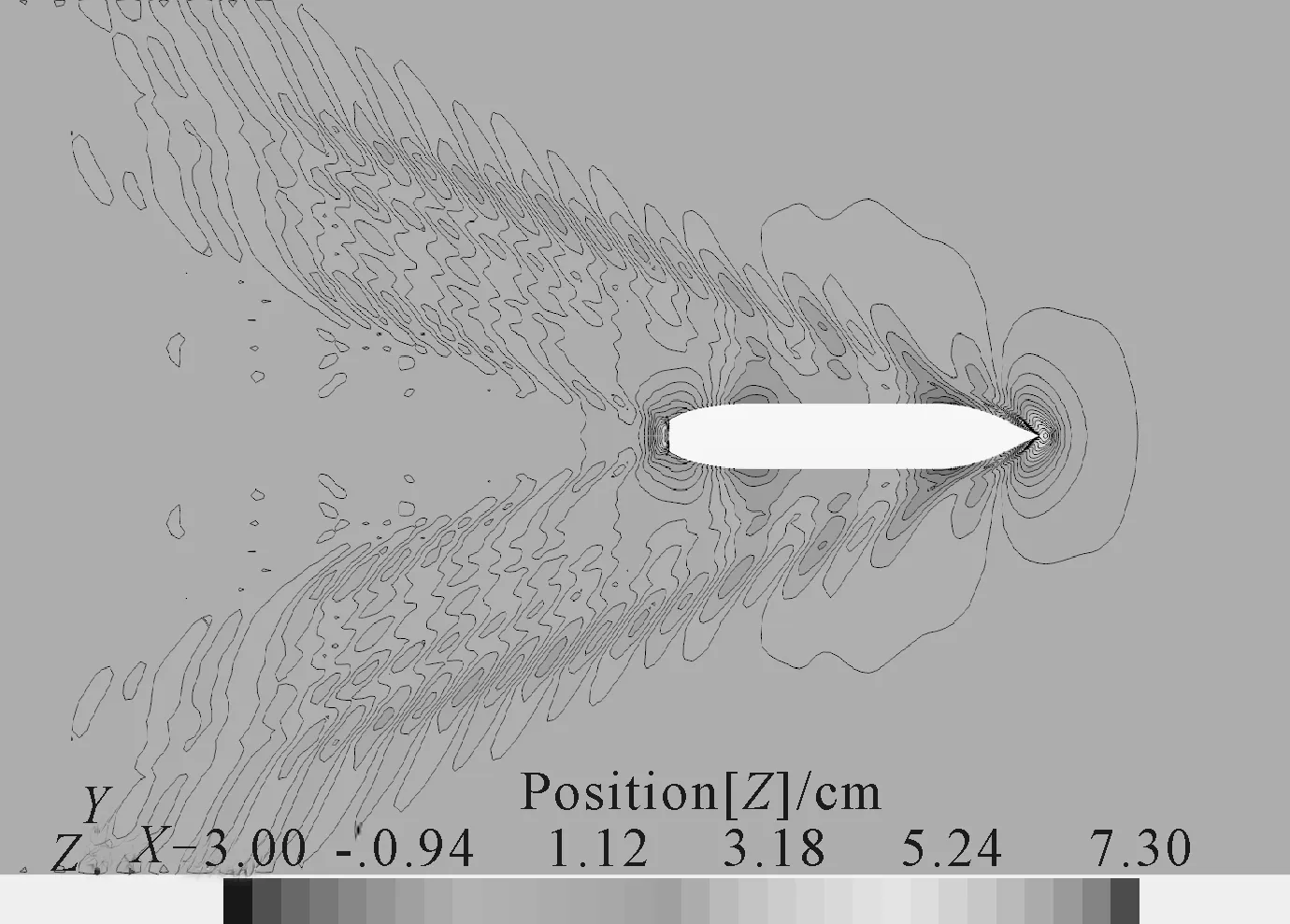
图5 CFD仿真结果波形图

仿真结果的最终值以计算状态稳定后，取100 s的均值，然后与试验结果均值进行比较。

其中，k-ε模型的计算结果的误差以三维的方式表示，见图6。

图6 k-ε计算结果误差

由图6可见，当Y+=60时，计算结果的误差均相对较大。与试验均值相比，3种网格数下的计算误差相较于试验均值的误差为-2.05%～-2.41%之间。这表明，近壁面处的处理对于仿真结果的影响最大。当Y+=120时，60万网格的计算结果较大于试验均值0.61%，114万网格的计算结果与试验结果完全一致，233万网格的计算值较小于试验均值-0.40%，总体而言，Y+为120时，仿真结果误差最小。当Y+为240时，3种套网格的结果均大于试验值，并随着网格数增加，误差由1.82%降低至0.49%。

k-ω的计算结果见图7。

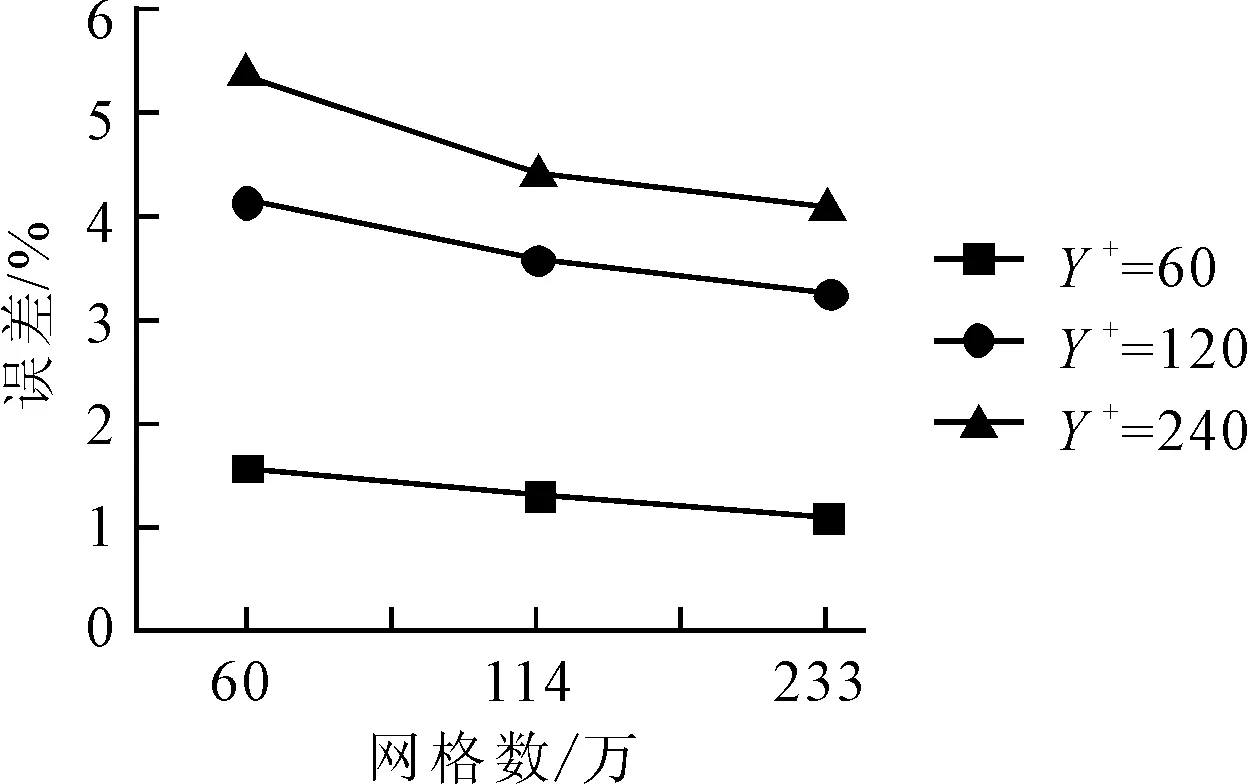
图7 k-ω计算结果误差

由图7可见，k-ω湍流模型的计算结果均高于试验值。其中Y+为60时，误差相对较小，随着网格数的增加，误差由1.57%降低到1.08%；而当Y+为120和240时，其仿真结果均大于3%；同时，以上结果也表明，随着网格密度的增加，仿真结果呈先下降趋势，并且114万网格的结果与233万网格的结果更接近。

SST的计算结果见图8。

图8 SST计算结果误差

由图8可见，Y+为60时，仿真结果较小于试验结果-2.90%～-3.65%；当Y+为120时，误差为-0.11%～-1.50%；当Y+为240时，结果误差范围为1.25%～-0.29%。SST模型的计算结果中，有3个结果落入了试验均值的不确定度范围内。同时，上图结果中SST模型对于网格的敏感度明显大于其他两种湍流模型。

综合分析以上结果，Y+明显对仿真结果产生了显著的影响，不同的湍流模型对于Y+的使用值并不一样。当Y+为60的时候，3种湍流模型分别对应的三套网格的计算结果的误差都是相对最大的，因此，在设置计算模型的时候，需要着重分析边界层处的处理，选择合适的Y+值。

网格密度的增加能够有效降低试验误差，随着网格密度的增加，计算结果之间的差值呈下降趋势。因此，在对结果精度有较高要求的时候，网格无关性的验证显得十分必要。

对于湍流模型的选择，需要慎重。如本文利用k-ω湍流模型的计算结果均是偏大于试验值，且偏差的绝对值也是处于较高水平。分析认为，k-ω湍流模型对于处理低雷诺数的湍流适用性更好，而船舶的阻力计算大多是高雷诺数的。SST模型虽然结合了k-ε模型在远场计算的优点和k-ω模型在近场计算的优点，但是仍然难以避免网格的高敏感度，以及剪切流动精度不高的问题，事实上，船身周围的流动都是包含剪切流动的。

需要说明的是，尽管对V=1.590 m/s时的标准船模进行了复合航次的阻力试验和CFD仿真的多维度计算，但并不一定适用于其他船型。

4 结论

1)在相同的湍流模型下，Y+对计算结果的影响要比网格密度的影响更大；随着网格密度的增加，仿真结果更加趋于稳定，但是该稳定值并不表示误差变小。

2)分别使用3种湍流模型计算，k-ε模型有部分结果与试验均值完全一致；k-ω模型的结果均大于试验均值1.08%～5.36%，对于高雷诺数模拟，该模型的结果并不可靠；SST模型的结果中，有3个结果落入试验结果的置信空间，这表明该模型相对稳定可靠，但是需要合理设置网格密度和Y+值。

3)仿真结果的精度及可靠性需要与可靠的试验结果对比，也需要针对具体的物理模型合理设置计算模型。