钢箱拱桥拱肋吊杆锚固区域力学性能数值分析

康俊涛 刘 开 邵光强

(武汉理工大学土木工程与建筑学院 武汉 430070)

0 引 言

近年来我国钢箱拱桥的建设不断增多，跨径也越来越大，同时对钢箱拱桥拱肋吊杆锚固结构的要求越来越高；但是拱肋吊杆锚固结构构造复杂，由各种形状的钢板焊接而成，不可避免的存在结构缺陷以及应力集中等问题，它们将对拱肋吊杆锚固结构的承载能力产生较大影响，进而危及整个钢箱拱桥的使用安全性.

钢箱拱桥拱肋吊杆锚固结构的研究主要集中在斜拉桥索梁锚固结构的疲劳分析及受力分析.万臻等[1]选择某桥最不利的索梁锚固段进行静载模型试验，采用空间有限元分析和足尺模型试验相结合的方法是研究索梁锚固区应力分布.周绪红等[2]为了掌握索梁锚固区在索力作用下的应力分布和极限承载力，对索梁锚固区在最不利荷载组合作用下的受力性能进行了研究，提出了改善索梁锚固区受力性能的构造措施.还有很多学者[3-6]对斜拉桥的索梁锚固区进行了试验以及相应的数值模拟研究；但是，斜拉桥的索梁锚固区域和钢箱拱桥的拱肋吊杆锚固区域结构形式及整体受力均存在差异，并且均未考虑箱梁节段在成桥状态下所承受的较大的轴力荷载.因此，考虑成桥状态下，对于承受较大拉力的钢箱拱桥拱肋吊杆锚固区域分析很有必要.

文中以某大跨度钢箱提篮拱桥为研究对象，在成桥最不利荷载组合作用下，计算出各钢箱拱节段两端承受的轴力和弯矩，并选出受力最不利的节段，建立精细化有限元模型，对钢箱拱肋节段吊杆锚固区域在承受较大吊杆拉力下的力学性能进行研究.

1 分析方法与试验对比

1.1 模型设计参数

赵秋等[7]为研究U形加劲钢板的失稳破坏机理，按不同的结构尺寸和不同强度组合的U形肋和被加劲钢板，设计制作了一组混合强度U形加劲肋钢板试件，进行了轴向加载试验.试件HJ2-2和HJ3-1的主要设计参数见表1，加劲钢板的断面示意图见图1.

表1 试件主要设计参数

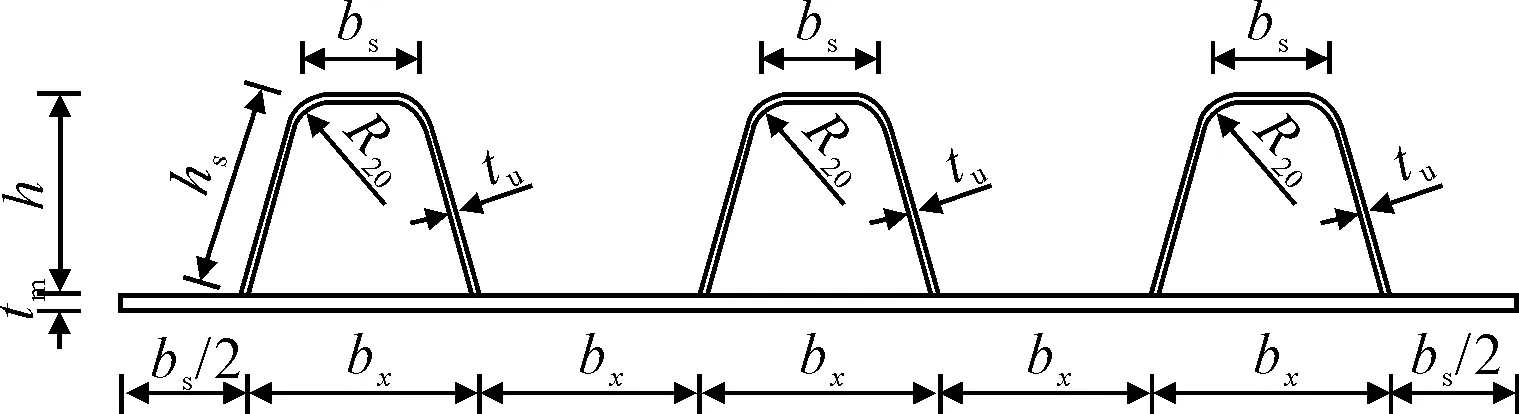
图1 试件断面示意

1.2 试验方案

1.2.1边界条件及加载方案

为了模拟试件两边铰接情况，在试件加载端和支承端设置了圆钢转动装置，释放了绕试件底端的转动约束.试验加载设备采用10 000 kN电液伺服长柱压力试验机.预压完成后，进行正式加载，采取分级单调加载，加载初期每级荷载增量为100 kN，当总荷载大于估算极限荷载50%时，采用位移加载，加载速率0.2 mm/min，直至试件破坏，加载示意见图2.

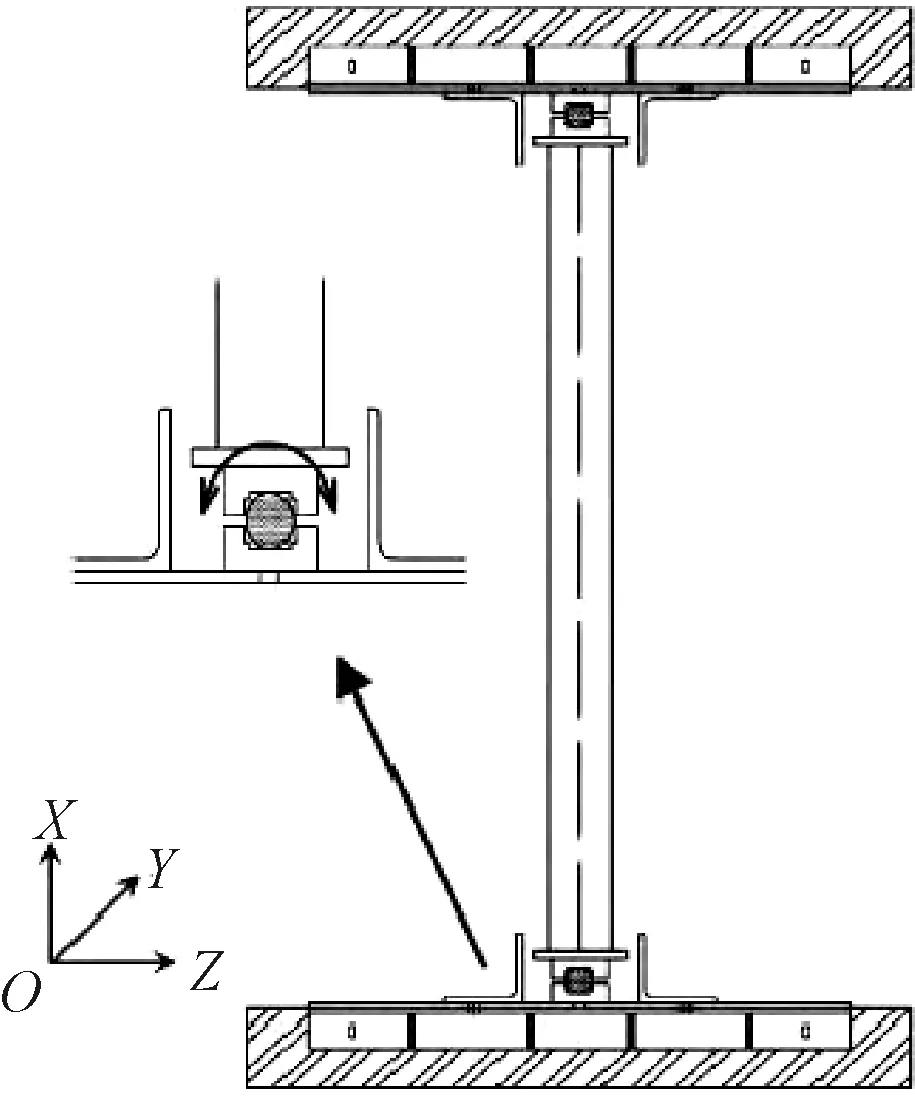
图2 加载示意图

1.3 有限元模型建立

采用ABAQUS软件对U形加劲肋钢板在荷载作用下失稳破坏机理进行有限元模拟.加载方式采用位移加载，有限元模拟采用弹塑性板单元来模拟，选用四节点四边形有限薄膜应变线性减缩积分壳单元(S4R)，该单元性能稳定，得到的位移和应力精度较高[8].

在有限元分析中控制单元边长为1 cm.综合考虑了材料非线性和几何非线性，采用自动增量步长法进行控制，通过残差力与位移修正值来判定迭代计算是否收敛.

1.4 数值模拟结果与试验结果比对

试验中得到U形加劲肋顶部的荷载-位移曲线，用荷载除以试件截面面积，得到截面平均应力.两个试件在受压过程中的平均应力-位移曲线实测值与数值模拟计算值的对比见图3.

图3 两个试件试验结果与数值计算结果对比

U形加劲肋钢板HJ3-1在荷载作用下的变形和数值模拟对比见图4.

图4 HJ3-1变形对比图

由图4可知，模型试验及数值模拟在轴向加载初期变形与平均应力基本呈线性变化，加载后期变形较大时发生屈曲，两阶段应力十分吻合，相对误差小于10%，并且构件的变形与模拟的变形结果相似.因此可以认为该数值模拟分析方法是合理可行的.

2 钢箱拱桥静力计算结果及分析

2.1 工程概况

该桥是跨径布置为48 m+196 m+48 m的大跨度钢箱提篮拱桥，主拱采用等截面钢箱型提篮拱，拱肋向内倾斜，与竖向成10°夹角；主拱矢高f=43.556 m，矢跨比为f/L=1/4.5，拱轴线为悬链线，拱轴系数m=1.6.主拱两拱肋间设置5道风撑，横撑采用箱型截面，见图5.

2.2 全桥有限元模型建立

采用大型有限元软件MIDAS/CIVIL，建立了全桥空间有限元模型.模型中采用设计截面和变截面等形式输入截面尺寸，较真实的反映了截面的抗弯、抗扭和抗剪等刚度特性.边界条件中，吊杆与主梁及拱采用弹性连接，主墩和边墩的支座采用一般支承，确保能够进行精确的桥梁结构整体分析[9].全桥模型共有1 105个节点，1 232个单元，全桥模型见图6.

2.3 成桥状态下静力分析

根据文献[10]可知，组合系数采用极限状态法取用，并考虑结构重要性系数γ0=1.1.全桥使用阶段静力分析时，采用的荷载组合为恒载+活载，该荷载工况下，结构的位移，内力和应力见图7.

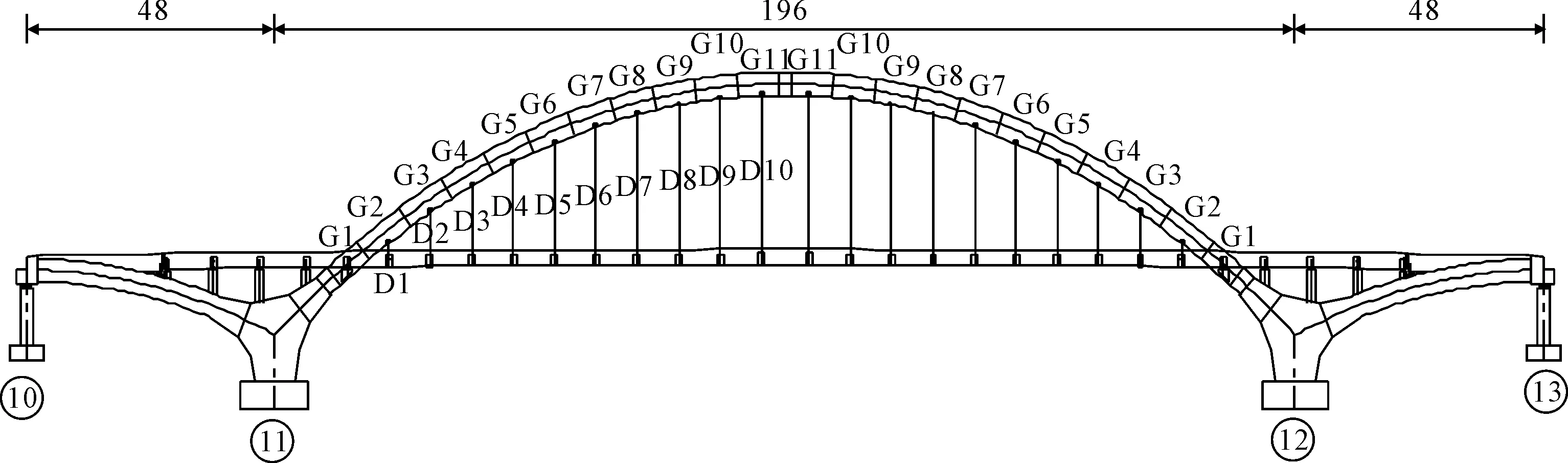
图5 桥型布置图(单位：m)

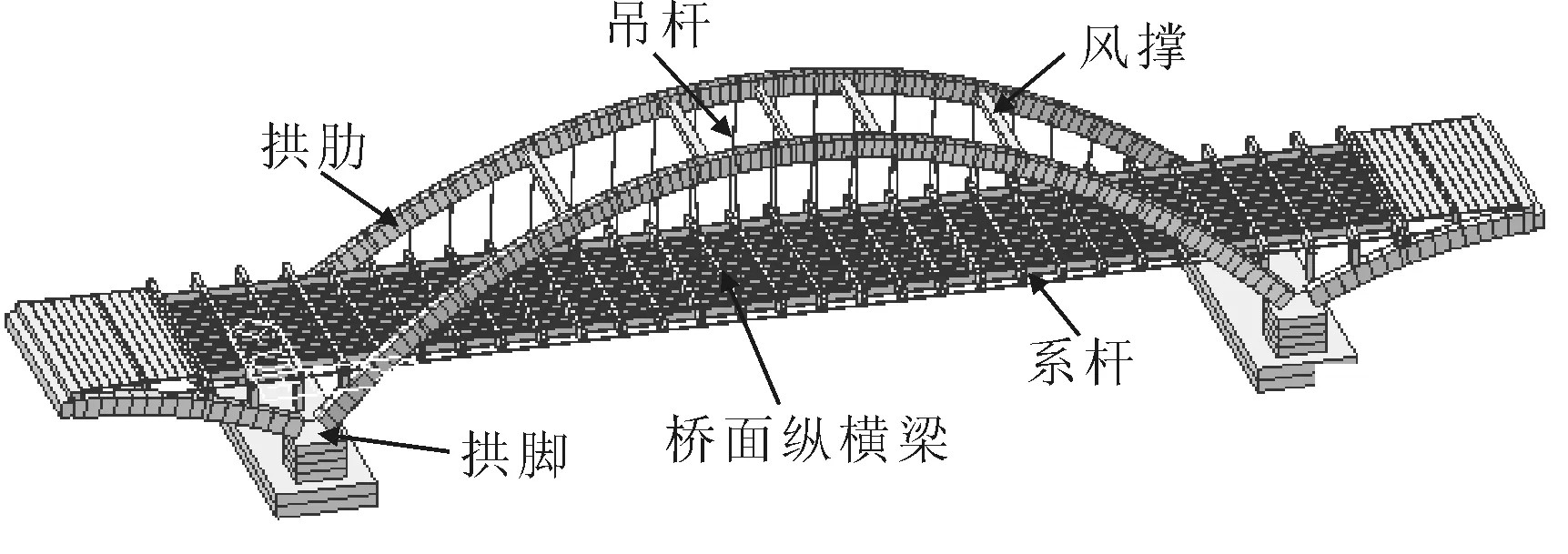
图6 全桥有限元模型

由图7可知，在恒载+活载工况下，桥面主梁产生竖向位移，最大为140 mm，出现在跨中位置；拱肋产生竖向下挠，最大下挠为80 mm，出现在拱顶位置；拱肋在拱脚位置产生最大轴压力为39 287 kN；拱肋最大面内弯矩值为17 511 kN·m，出现在拱顶位置；拱肋最大面外弯矩值为8 598 kN·m，出现于拱脚处.

图7 结构位移、内力和应力图

2.4 钢箱拱各节段受力

钢箱拱桥主拱肋主要由编号为G0～G12的共50个钢箱节段焊接而成，每一个钢箱节段两端均承受较大的轴力和弯矩.受力情况见表2.

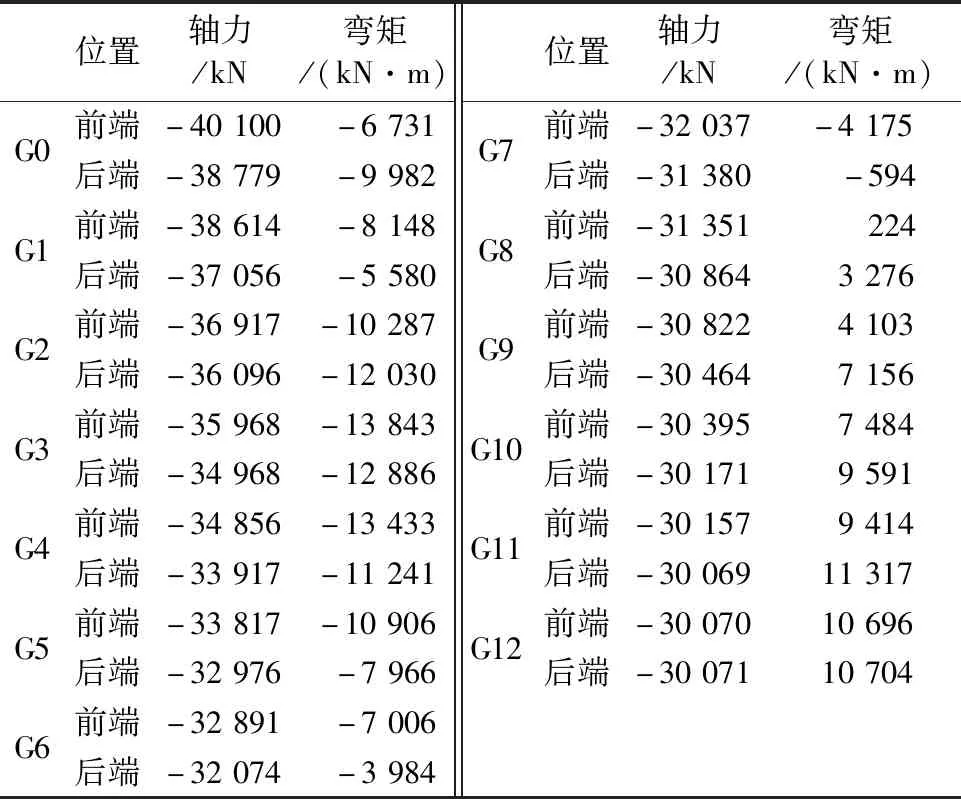
表2 钢箱拱肋节段受力

各节段前端轴力变化趋势见图8.

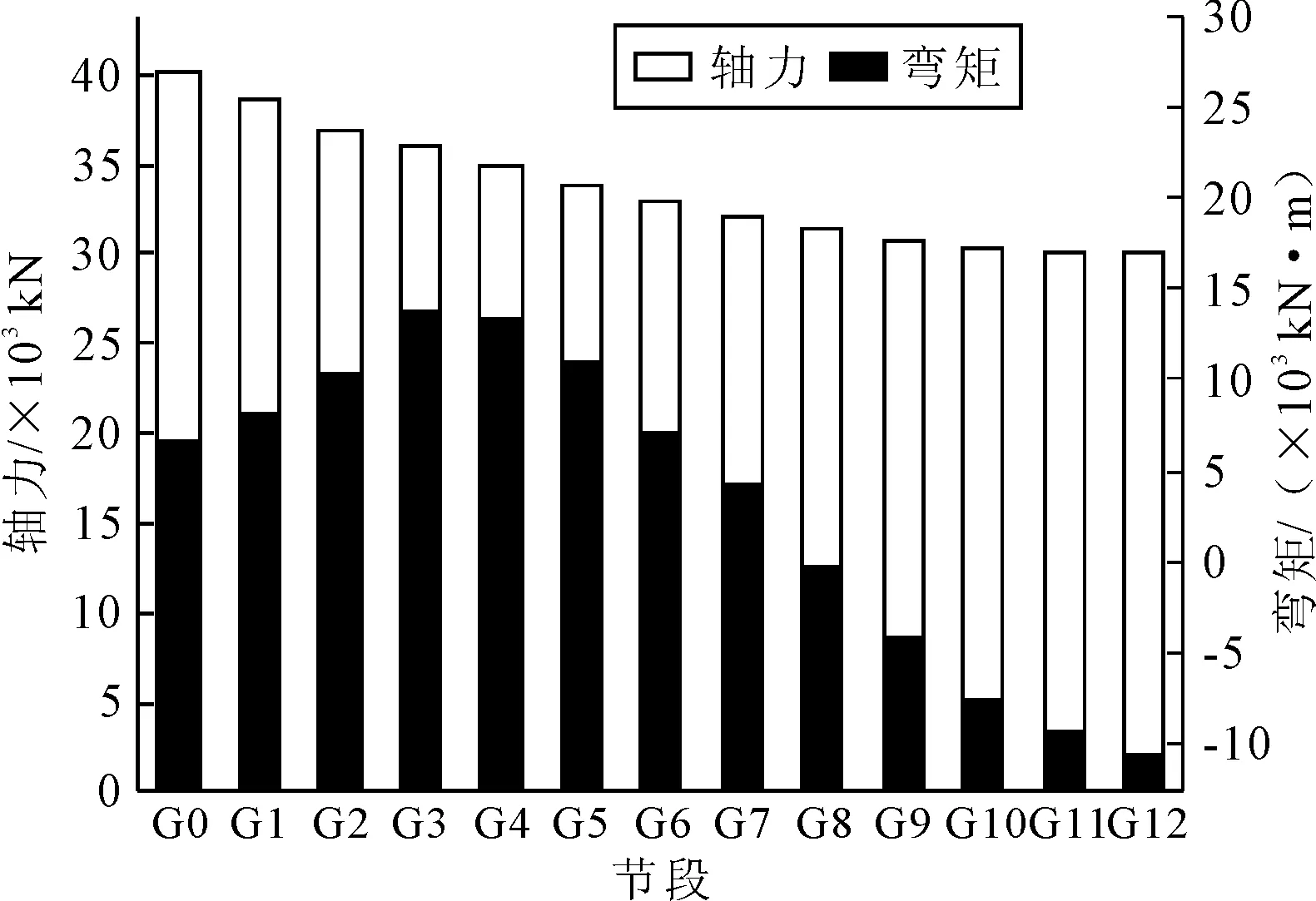
图8 节段前端轴力弯矩变化

各拱肋吊杆最不利状态成桥状态下的拉力见表3.

由图8和表3可知，钢箱节段由两边向中间变化的过程中，轴力越来越小.靠近拱脚的节段承受负弯矩，其中G3节段负弯矩最大，达到-13 843 kN·m；跨中截面承受较大正弯矩，其中G11节段正弯矩最大，达到11 317 kN·m；成桥状态下，D4吊杆的拉力最大，即G5节段承受的拉力最大，为1 939 kN.

表3 钢箱拱肋节段受力

3 拱肋吊杆锚固区域分析

全桥在G2～G11节段上分别安装了D1～D10，共40根吊杆，由之前计算可知，G5节段承受的吊杆拉力最大，因此选出G5作为最不利节段，研究拱肋所能承受的最大的吊杆拉力，并对拱肋吊杆锚固区域的各个板件进行力学性能分析.

3.1 拱肋节段概况

G5节段是主拱圈靠近1/4跨位置处的节段.G5节段长8 826 mm，仰角为25.0°，箱室的内部截面为400 mm×250 mm的矩形.该拱肋顶底板厚度采用40 mm，腹板采用36 mm；顶底板及腹板采用板肋进行加劲，加劲肋厚度为24 mm.吊杆锚固区域是由各个不同形状的板件焊接而成.

3.2 拱肋节段有限元模型建立

3.2.1单元划分及模型尺寸

采用软件对钢箱节段进行有限元模拟计算，大小与实际尺寸相当.为了有效地模拟节段的实际情况，钢箱节段两端的横截面采用固定约束，并施加计算出的轴力、剪力、弯矩荷载，作用在锚固结构上的吊杆拉力采用位移加载的方式，在锚固区域吊杆安装部位中心建立一个参考点，对该点施加竖向位移荷载，每一次加载的位移步长为1 mm，有限元模拟采用弹塑性板单元来模拟.网格划分见图9.

图9 网格划分

3.2.2材料本构与加载方式

钢材弹性模量为2.0×105MPa，泊松比为0.3.钢板选用Q345钢材.材料屈服准则为Mises屈服准则，采用多线性随动强化理论刻画钢材屈服后行为，详细本构特征见图10.Q345钢材在应力为345 MPa时进入屈服阶段，随后达到极限强度600 MPa，最后应力减小进入颈缩阶段[11-13].

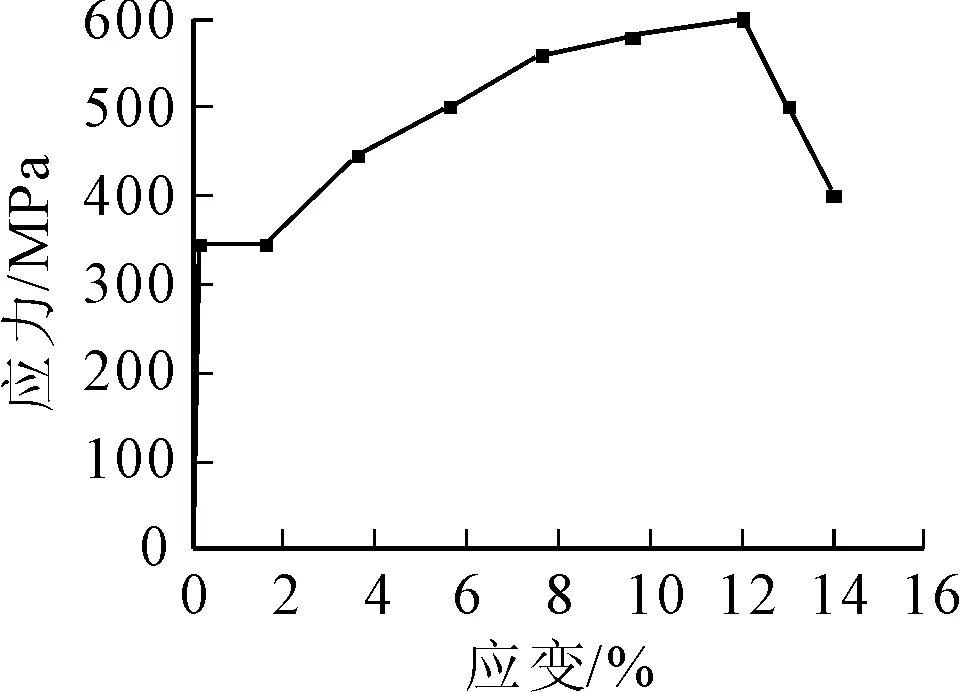
图10 应力应变关系

采用位移线性加载方式，最大加载位移为30 mm.

3.3 结果分析

3.3.1承受最大吊杆拉力分析

在位移加载过程中，锚固区域承受吊杆拉力逐渐增大，当达到极限承载能力，锚固区域的钢板发生大变形之后，锚固区域承受的吊杆拉力达到峰值.图11为锚固区域的竖向位移和承受吊杆拉力的关系图.

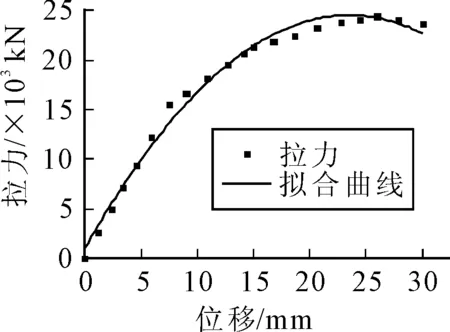
图11 锚固区域拉力位移关系

由图11可知，在前期位移荷载增大的过程中，拉力逐渐增大到15 000 kN，拉力和位移基本呈线性变化；后期，随着位移荷载继续增大，拉力越来越大，但是增大的速度会放缓，直至拉力达到24 000 kN后不再增加.

3.3.2拱肋节段两端荷载影响分析

在成桥下，钢箱拱肋节段两端承受较大的轴力以及弯矩荷载，对施加端部荷载前后锚固区域承受最大吊杆拉力进行分析，见图12.

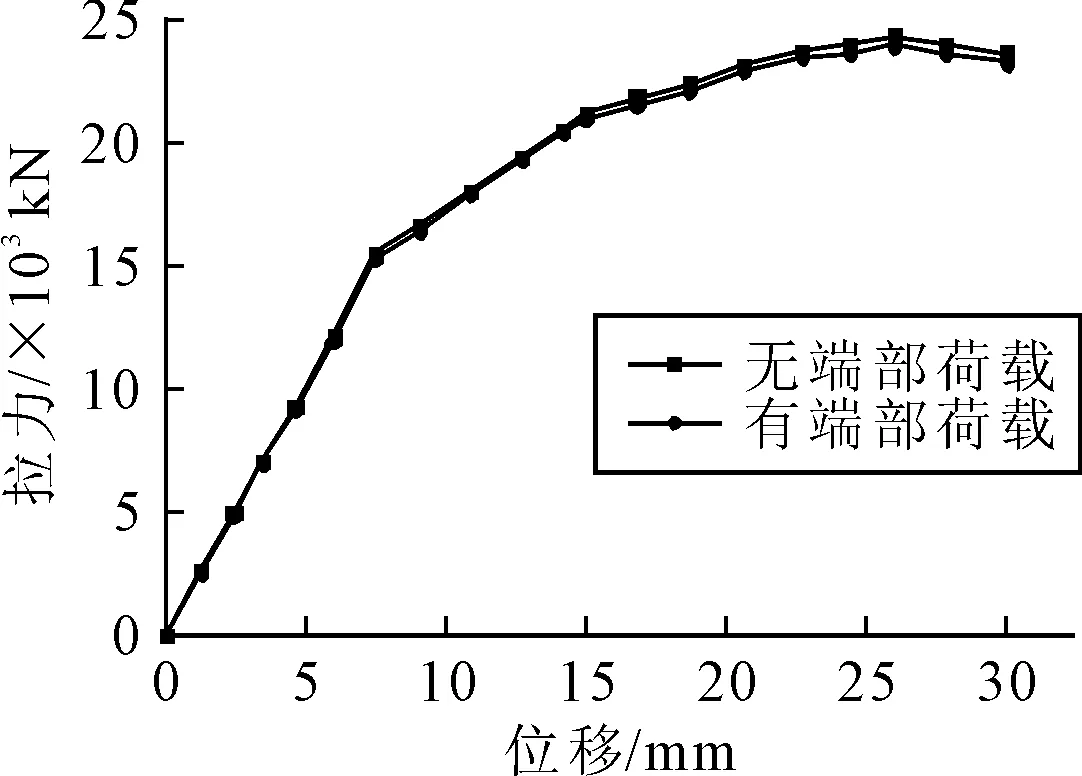
图12 端部荷载对拉力影响

由图12可知，在钢箱拱肋节段两端承受较大的轴力以及弯矩荷载时，锚固区域承受拉力荷载的能力会有所降低，比无端部荷载作用时减小约0.5%.

3.3.3锚固区域各板件应力分析

通过ABAQUS建立精细化板单元结构模型，计算出各板件的应力，并将受力最不利的两部分板件由图13列出.

图13 应力云图(单位：Pa)

由图13可知，在进行位移加载过程中，吊杆锚箱的两块横隔板首先达到极限强600 MPa，并发生大变形破坏；拱肋底板处，与吊杆锚箱连接处的应力最大，为510.2 MPa，应力的大小由中心向四周扩散分布.同时，由于仅仅是锚固区域局部发生大变形，整体钢箱节段钢板并未达到极限强度，因此在锚固区域承受的拉力并未呈现明显下降趋势.

4 结 论

1) 在钢箱拱肋节段两端承受较大的轴力以及弯矩荷载时，锚固区域承受拉力荷载的能力会有所降低，比无端部荷载作用时减小约0.5%.

2) 在位移加载过程中，锚固区域承受吊杆拉力逐渐增大，当达到极限承载能力，锚固区域的钢板开始发生大变形，但由于钢箱节段钢板并未达到极限强度，因此锚固区域承受吊杆拉力的能力并未明显下降.

3) 在进行位移加载过程中，吊杆锚箱的两块横隔板首先达到极限强600 MPa，并发生屈曲破坏；拱肋底板处，与吊杆锚箱连接处的应力最大，为510.2 MPa，应力的大小由中心向四周扩散分布.

基于以上研究成果，可以根据构件的受力状态及变化规律对拱肋节段的各板件进行优化设计，在节约工程造价的同时降低桥梁自重，提高各构件的承载效率，为同类型桥梁的设计提供参考和借鉴.