一种简化的布谷鸟搜索算法
李 辉
(福建水利电力职业技术学院 基础部数学教研室, 福建 永安 366000)
0 引 言
优化问题广泛存在于生活生产实践的各个领域,其主要目的是从众多方案中选取一个(一些)性能指标达到最优的方案,随着人类社会的不断进步和发展,优化对象越来越复杂,规模越来越大,条件越来越苛刻,传统的优化手段很难处理,很多学者提出了智能优化算法,如遗传算法、粒子群算法、蛙跳算法、人工鱼群算法、蜂群算法等。该类算法模拟自然界动物特性进行寻优,对目标函数相关信息要求比较少,且便于改进和融合,因而日渐成为学界的研究热点。
布谷鸟搜索算法(Cuckoo Search,CS)是由剑桥大学学者Yang和Suash于2009年提出的,该算法搜索机制简单,参数少,易于实现,提出后受到很多学者的关注,如孙敏等人[1]通过自适应调整步长因子提高算法性能,叶亚荣等人[2]通过随机扰动提高算法的收敛速度,张海南等人[3]将蚁群算法与布谷鸟搜索算法融合,提出了交互式学习的布谷鸟算法,而宋庆庆等人[4]则结合了拟牛顿算法对布谷鸟算法进行改进等。同时,也有学者将布谷鸟算法应用于梯级水库调度优化[5]、边坡滑面搜索[6]、色彩图像分割[7]等。
但该算法搜索性能仍有待提高,本文进一步简化布谷鸟搜索算法的机制,进化时充分利用群体信息,极大地提高了算法的收敛速度和精度,并且将本算法应用于求解约束优化问题,取得了较好的结果。
1 基本布谷鸟搜索算法
基本布谷鸟搜索算法通过引入鸟类的莱维飞行机制,模拟布谷鸟的产卵行为进行寻优,该算法设有3条规律,分别阐述如下。
(1)一只布谷鸟每年只产一个卵,并且随机地选择一个鸟巢进行孵化。
(2)具有最好的卵的鸟巢将被保留下来。
(3)鸟巢按一定概率被发现,鸟巢一旦被发现将被舍弃或者重新选位置修建。
在布谷鸟搜索算法中,个体位置更新利用莱维分布来实现,个体i的位置更新公式为:
xt+1i=xti+α·L(λ),
(1)
其中,α为步长因子,根据具体的优化问题而定,一般取值为1;L(λ)为服从参数为λ的莱维分布,即:
(2)

基本布谷鸟搜索算法首先在可行域内产生一组初始个体,确定最优个体xtb,然后保留最优个体,对其他个体按照式(1)进行位置更新,若新个体更优,则替换;对每一个个体按概率Pa进行变异,即对于个体i,若Pa小于一个均匀分布的随机数,则重新随机产生一个新个体xnew,若xnew优于个体i,则替换,否则不替换。循环进行,直到达到收敛条件。
分析可知,基本布谷鸟搜索算法中的莱维分布过于复杂,个体在更新过程中利用了自身信息和最优个体的信息,但是在变异时随机产生新个体,没有充分利用群体信息,容易延缓算法的收敛速度,且基本布谷鸟搜索算法收敛精度不高,考虑到这些不足,本次研究简化了个体更新算法,将莱维分布函数进行了简化,便于操作和实现,同时,利用个体自身适应度和最优个体的适应度进行变异,有效地解决了算法复杂,收敛性能较差的问题,本文提出了一种改进的简化布谷鸟搜索算法(A simplified cuckoo search,SCS)。
2 一种简化的布谷鸟搜索算法
莱维分布是鸟类的莱维飞行机制的反映,但是计算偏于复杂,不便于广泛应用,且严重影响计算速度,因此,文中将莱维分布进行了简化,即对于个体i按照以下方式进行位置更新:
xt+1i=xti+α·L,
(3)
(4)
其中,v~N(0,1),u~N(0,2),当随机数r>Pa时,对个体i按下式进行更新:
(5)
其中,fit(xi)为个体i的适应度,ε为一个极小的数,防止分母为零。
改进的简化布谷鸟搜索算法流程可表述为:
Step1初始化。在可行域内随机产生n个初始个体,设置步长因子α,变异概率Pa,最大迭代次数T,记录当前最优个体xtb。
Step2局部搜索。对除最优个体之外的所有个体按照式(3)和式(4)进行更新,若新个体更优,则替换,否则不替换。
Step3随机变异。对于每一个个体xti,随机产生一个均匀分布数r,若r>Pa,则对个体xti按式(5)进行变异,若新个体优于原个体,则替换;否则,保留原个体。
Step4判断停机条件,达到则输出最优解;否则,转Step 2。
3 实验及结果分析
本文使用常用的4个测试函数,对算法的性能进行检验,测试函数见表1。其中,函数f1为单极值函数,函数f3和函数f4为多极值函数,根据经验,目标最优值设置也参见表1,由于函数f2的全局最优点位于一个平滑、狭长的抛物线形山谷内,由此可推得,目标精度通常为30。相关参数设置为:个体数为30,步长因子α=1,变异概率Pa=0.25。
表1 测试函数
Tab. 1 The test functions

名称公式维数搜索范围理论最优值目标最优值Sphere f1f1(x)=∑ni=1x2i30[-100,100]n01E-15Rosenbrock f2f2(x)=∑n-1i=1(100(xi+1-x2i)2+(xi-1)2)30[-100,100]n030Rastrigrin f3f3(x)=∑ni=1(x2i-10cos(2πxi)+10)30[-100,100]n01E-15Griewank f4f4(x)=14 000∑ni=1x2i-cosxii+130[-600,600]n01E-15
DCBA和BA对4个函数的进化对比如图1所示。图1中,横轴为算法迭代次数,纵轴为全局最优值,最大迭代次数为100,CS为基本布谷鸟搜索算法进化曲线,SCS为本文算法进化曲线。从图1中可以清楚地看出:改进的简化布谷鸟搜索算法对4个测试函数的搜索速度和精度都非常出色,都可以在极少的迭代次数下找到目标最优值。
将改进布谷鸟搜索算法的搜索性能与基本布谷鸟搜索算法和文献[8]中的算法进行比较,所得结果见表2和表3。其中,CS表示基本布谷鸟搜索算法,MPCS表示文献[8]中的算法,SCS表示本文中的改进算法;所有算法的最大迭代次数均为500次,超过500次仍没有达到目标最优值,则认为算法不收敛。可以看出,改进布谷鸟搜索算法的收敛精度比其它算法都高,且所需迭代次数非常少。该算法可在极少的迭代次数下搜索到函数1、函数3和函数4的理论最优值,也可以迅速找到函数2的目标最优值、且收敛率都是100%。
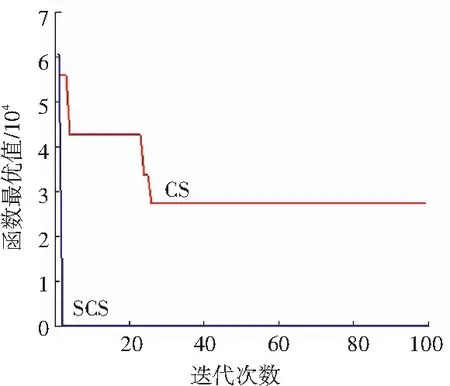
(a) 函数f1

(b) 函数f2

(c) 函数f3
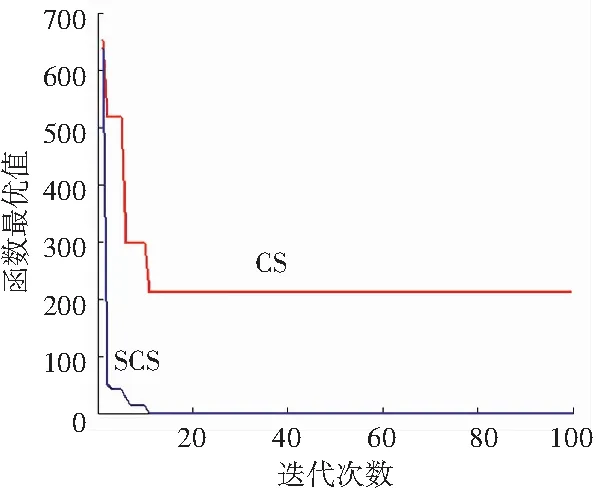
(d) 函数f4
Fig. 1 The convergence speed and accuracy of 100 times' iteration
表2 SCS算法与其他算法收敛精度的比较
Tab. 2 Comparison of search accuracy between SCS with other algorithms

函数算法最优值最差值平均值f1CS1.252E-166.578E-151.459E-15MPCS2.617E-179.610E-162.252E-16SCS000f2CS67.3941 720.215459.460MPCS60.2801 110.784272.477SCS28.01329.89628.214f3CS1.7319.0686.179MPCS1.4294.9803.213SCS000f4CS2.357E-031.365E-017.017E-02MPCS1.166E-031.539E-013.707E-02SCS000
表3 SCS算法与其他算法收敛速度的比较
Tab. 3 Comparison of search speed between SCS with other algorithms

函数算法收敛所需最小迭代次数收敛所需最大迭代次数收敛所需平均迭代次数收敛率f1CS955998982.2012/20MPCS913997956.2020/20SCS936.1320/20f2CS691994831.300/20MPCS540947722.500/20SCS122015.2020/20f3CS500991802.400/20MPCS189984416.900/20SCS18712.3220/20f4CS753986908.000/20MPCS664931806.300/20SCS1158.3020/20
4 算法的应用
4.1 带约束的单目标优化问题
单目标约束优化问题基本模型如下:
minf(x1,x2,…,xn)
(6)
本文在可行域内给定初始解,通过改进布谷鸟搜索算法进行不断迭代,直到找到最优解。对于约束条件,文中使用罚函数法,即做如下数学定义:
F(x1,x2,…,xn)=f(x1,x2,…,xn)+
(7)
其中,λ,γ为惩罚因子,取比较大的正数。
因此,带约束的单目标优化问题解决思路为:在可行域内给定初始解,作为初始个体,按照式(7)计算适应度值,记录最优个体和当前最优值,并根据改进的简化布谷鸟搜索算法进行寻优,直至找到最优值,记录最优个体,计算求出原目标函数的最优值。
4.2 数值实验
通过以下约束优化问题检验DCBA算法的性能:
(8)
该函数的理论最优值为2.2。采用本文提出的简化布谷鸟搜索算法进行寻优,定义适应度函数为:
F=4x1+x2+x3+λ((2x1+x2+x3-4)2+(3x1+3x2+x3-3)2)+γ(x12+x22+x32).
(9)
设置最大迭代次数为500次,步长因子取5,设置不同惩罚因子时搜索到的最优值见表4。当惩罚因子逐渐增大时,最优值不断稳定于2.2。
表4 不同惩罚因子下目标函数的最优值
Tab. 4 Optimal value of objective function under different penalty functions

惩罚因子λ惩罚因子 γ最优值2002002.435 12005002.301 22001 0002.295 15001 0002.300 11 0005 0002.248 51 00010 0002.202 22 00010 0002.201 710 0001 000 0002.200 1
5 结束语
本文将布谷鸟搜索算法中的莱维分布函数进行了简化,提出了一种简化的布谷鸟搜索算法。该算法中不仅个体更新的莱维分布函数更加简单易算,而且在个体变异时,还引入了适应度信息,加快了算法的寻优速度,数值实验发现,该算法不仅操作简单,且寻优性能非常理想。同时,本文将新算法用于求解约束优化问题,发现其寻优效果也非常好。因此,改进的简化布谷鸟搜索算法是一种简单易行、鲁棒性高、融合性强的高性能寻优算法。

