不同内径和厚度的立井受力研究

张文辰

(安徽理工大学 土木建筑学院，安徽 淮南 232001)

地下立井井壁破裂问题，一直是制约地下矿业和地下建筑发展的一个重要问题，长期以来，地下立井井壁发生破裂的事故时有发生，严重之时，甚至会威胁地下作业人员的生命财产安全。

在对立井井壁发生破裂的理论研究中，大部分研究学者均认为[1-9]，造成立井井壁破裂的原因，是由于表土沉降对立井井壁产生负向互动摩擦力所致。因此设计人员在此研究的基础上，提出了复合式井壁设计理论和卸载槽处理事故方法，这些理论和技术方法的提出，虽然对立井井壁破裂问题起到了一定的积极性作用，但也没有从根本上解决和预测立井井壁破裂问题，原因是由于在特定时间和特定温度下，井壁的特定位置依然出现井壁破裂现象，故此可以说明上述理论和技术方法依然难以满足预测和防范立井井壁发生破裂问题[10]，因此在上述研究理论的基础上再进行深入的井壁破裂因素研究已十分必要。

基于上述原因，作者在经过对立井井壁负向滑动摩擦力的成因进行细致及深入的分析研究后发现，产生负向摩擦力的主要起因是来自于井筒内外的温度变化，在井筒内外温度发生改变时，来自井筒内外的温度应力随之作用于井壁之上，造成井壁产生破裂，在该解释的支撑下，不仅所有井壁破裂特征均能得到解释，同时对于预测井壁破裂、深井井壁设计均提供了理论依据。

由于造成立井井壁破裂的作用力最终作用对象是立井井壁，因此立井井壁的组大应力荷载是否满足立井各方面的应力总和，是导致立井井壁产生破裂的基础条件，因此研究井壁应力荷载及井壁各应力的荷载情况，是为日后各地下立井工程设计修建提供具体的数据理论参考。

1 立井概述

1.1 地下停车场基本参数

以某地下停车场为背景，具体参数如表1:

表1 地下停车场立井参数表

1.2 受力分析

地下停车场由于处于深厚表土层，因此立井处于一个温度和地下水位变化的环境之中，在这个环境里，立井同时受到来由温度变化引发的温度应力、井体自重和来自土层的水平地压[10]。

1.2.1 重力应力

(1)井壁自重

立井井壁自重作用力主要来源于地心对井筒所附加的引力，其计算公式可表达为：

G1=ρcgHπ(D2-d2)/4(单位：N)

(1)

式中，pc为立井钢筋混凝土的重量；H为立井所计算断面的埋深，具体受力情况如图1所示。

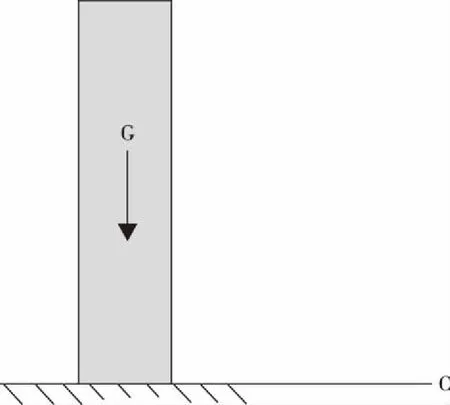
图1 井筒自重受力图

(2)井内钢结构、绞车及车重

立井纵向高度200m，每层高2m，约100层。每层停6辆车，每辆重1.6t；每层钢结构重20t，绞车重50t，则井筒内部满载重量G2约为3.01×107N。此时立井总总自重力G=G1+G2，则总重力导致的竖向应力可以表达成：

(2)

1.2.2 地表沉降及井筒深长导致的滑动摩擦力产生的应力

在冻结壁融化阶段，冻土融化发生收缩，井壁因温度升高而膨胀延伸；在使用过程中，尤其在气温相对较高的夏天时，由于地下水位的降低，井筒周围的表土会沉降，而井筒内壁由于通风系统的影响会保持较高温度而使井筒进一步伸长。受上述两方面影响，井筒和表土会发生相对移动，此时井筒受到表土施加的方向向下的动摩擦力，受力如图2所示：

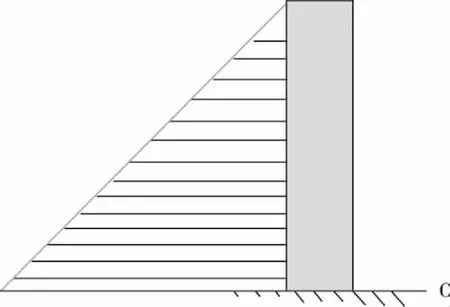
图2 立井滑动摩擦受力图

此时在底面C处的摩擦力可表示为:

fc=γegHλπK0πD(单位：N/m)

(3)

则滑动摩擦对底面C处的应力可表达为：

(4)

1.2.3 温度应力

根据相关研究资料发现，对于立井井壁的温度应力产生，主要受到以下三个方面的影响：一是由立井内外温度变化引起的负向摩擦力造成的温度应力；二是立井内外温度存有一定的高低差别，进而产生的温度应力；三是，当立井受到地层温度影响，井壁温度升高，进而产生热胀冷缩现象，当井筒发生径向膨胀之时，又因土层的隔阻，产生的温度应力。由于在1.2.2节中，已经对第一种由温度变化产生的温度应力进行了分析，故此下面只讨论后两个因素所产生的温度应力。

(1)井筒内、外壁温差产生的温度应力

由于立井纵深时井壁外沿一般会经过温度变化趋向稳定的第四纪冲积层，故此当立井内部空气温度相比地层温度较高时，由内外具有一定的温差，进而在立井井壁外沿产生一定的竖向温度应力，这种温度应力的作用方向是多样的，其中包括环向温度应力和径向温度应力。

对于两端自由的空心圆柱体，其温度应力计算可表示为：

(5)

(2)井筒径向膨胀受阻产生的温度应力

当立井井筒温度发生变化，井壁发生热胀冷缩现象，在此时间，立井井壁除了发生纵向的延伸之外，同时也会发生水平面的径向位移变化。当井壁发生水平位的径向位移之后，由于立井井壁外被表土层所包围，因此当井壁发生径向位移之时，同时也会受到表土层水平面负向的挤压作用力。此处为了简化研究，仅考虑了温度对立井井壁的影响，计算过程将不考虑地压对立井井壁的反向作用。

设置参数qb为立井受热膨胀时表土对立井井壁施加的应力，该应力的求解，根据相关资料说明，以静不定理论[17]、Winkller 地基模型及轴对称厚壁圆筒的弹性理论为参考[15,21,22]。三者之间的变化关系，利用力学静不定理论，可表达成：

b∈θ=S+ub

(6)

上式中的εθ可由式(4)，(5)中的第二式求得，而S 及ub可根据 Winkller 地基模型和轴对称厚壁圆筒的弹性理论分别求出为：

(7)

式中，k为基床系数，代表发生单位位移时所产生的负向作用力由于此处不考虑地压的影响，因此，k 仅与表土的性质有关，取k=4.0×107N/m3； S 为外井壁在温度及表土共同作用下产生的位移，单位为 m；ub为外井壁在压力qb作用下产生的径向位移，单位为 m。将外半径b，内半径a，弹性模量E，泊松比μ代入上面方程，可以求出由于膨胀受阻的反向作用压力qb。

在这种情况之下，利用弹性理论[15-16]中的拉密解答方法可以求得井壁中径及井壁环向应力，其解答的方式为(8)和(9)：

(8)

(9)

在得出(8)、(9)式后，利用广义虎克定律求得相应的竖向应力为：

(10)

1.2.4 水平地压

以图1为例，深度为y的立井地压计算公式为：pb=γegyλ，则立井底部的C处地压值pbc=γegHλ。此种情况下，井壁中因地压作用而产生的径向及环向应力均可由弹性理论中拉密的解答求出，即式(11)；(12)：

(11)

(12)

由于该问题和(8)、(9)同属于平面应变问题，使用相同解释方法可求得相应竖向应力，即：

σzb=μ(σbr+σbθ)

(13)

将上述计算产生的应力相加，得到各方向的总应力如下式所示：

(14)

进而求得最大总应力为：

(15)

考虑到混凝土井壁在很多情况下呈现剪切破坏的特性，因此对于井筒应力计算结果，应采用库伦-纳维尔准则校核，即：

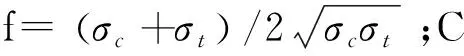
2 深200m内径宽度不同的井壁厚度受力分析

2.1 环境参数

为了保持计算的一致性，以下分析过程中，下列参数保持不变：井壁混凝土强度等级σc= 70MPa，安全系数2.0，σt= 4.5 MPa，钢筋混凝土体积密度ρc=2 500 kg/m3，弹性模量 E= 37GPa，泊松比μ= 0.18，热膨胀系数 αf=10×10-61/℃；内井壁温度Ta=30 ℃，外井壁温度Tb=17 ℃，冻结时温度To=-10℃，表土密度γe=1900 kg/m3，静摩擦系数 k0= 0.3，侧压系数λ= 0.333，基床系数k= 40×106N/m3。

2.2 立井内径15m的井壁不同厚度受力分析

在实际地下停车场修建中，由于很少出现类似矿井发生表土沉降的现象，因此当工程设计修建之时，如果不需要考虑表土沉降对立井井壁的影响，则可按照以上立井井壁受力计算方式进行受力计算，在此时，可将地表沉降及井筒深长导致的滑动摩擦力σzf忽略，其他计算方法不变。其计算过程及结果如以下几节。

2.2.1 壁厚1.0m的井壁受力分析

此情况下，立井内径d为15m，外径D=内径和壁厚之和，即d+(1.5×2)=17/m,内半径a=d/2，即7.5m，外半径为a+1，即8.5m。

根据以上参数，下面分别对立井重力、地表沉降或筒长导致的滑动摩擦力、温度应力、水平地压产生的应力以及总竖向应力进行分析。

(1)重力

根据式立井井筒和附加物的总重力计算公式(1)，计算出井筒总重力G=2.8×108N，然后带入式(2)进行井筒重力导致的竖向应力计算，最终得到立井竖向应力为5.6Mpa。

(2)地表沉降或筒长导致的滑动摩擦力

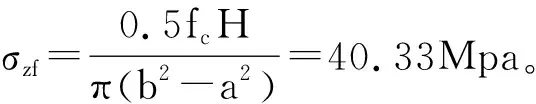
(3)温度应力

根据上文的分析，井筒温度应力主要来源于两个方面，一是井筒内外温差所产生的温度应力，一是井筒径向膨胀时受阻产生的温度应力。以下将对这两方面进行计算。

①井筒内外温差所产生的温度应力

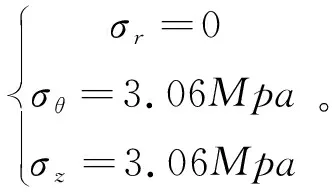
②井筒径向膨胀时受阻产生的温度应力

同理，将井筒内半径参数带入式(8)、(9)进行计算，然后利用广义虎克定律将式(8)、(9)的计算结果带入式(10)进行计算，最后求得

(4)水平地压产生的应力

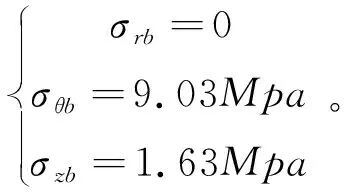
(5)总竖向应力

根据上述计算，分别将结果代入式(14)，分别得到井筒的环向、竖向、径向总应力为：

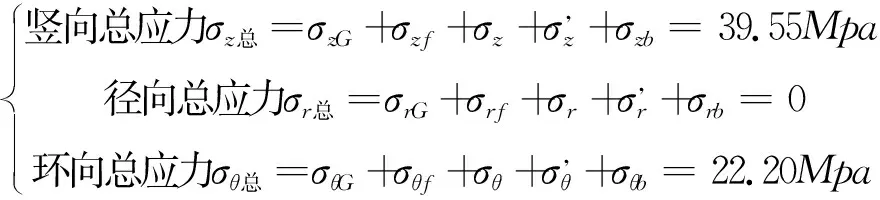
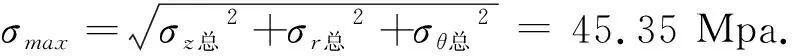
2.3 壁厚1.5m至3.0m的受力情况

按照上节计算方法对内径为15m的立井不同壁厚情况进行受力计算，得到表2：

表2 内径15m的立井各厚度受力表(单位Mpa)

从表2的数据中，可以看到，随着井壁厚度的增加，立井各受力值一直呈递减状态。在不考虑混凝土强度及项目安全系数的情况之下，内径为15m的立井，井筒在壁厚为1m和1.5m时，所收到来自4各方面的应力总值最大，为45.35Mpa。

由于本次研究的地下停车场立井采用混凝土强度为C70，安全系数为2.0的工程标准，因此在井深为200m，内径15m的条件下，井壁厚度以0.1m的递增趋势按照以上计算，要满足地下停车场工程修建标准，即最大应力为35Mpa时，立井井壁的厚度为2.6m。经计算，井壁厚度为2.6m时，作用在立井上的各方向应力数值结果如下：

此时，

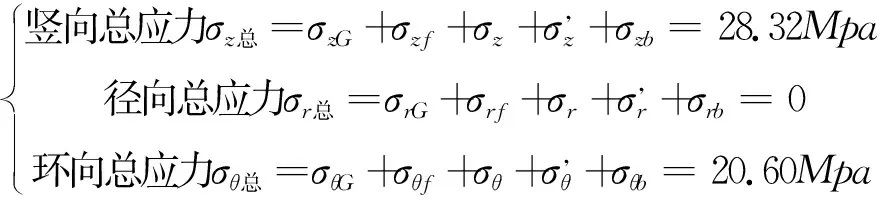
经校核，满足库伦-纳达尔准则。

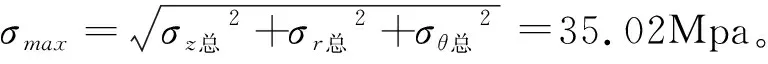
2.4 内径20m不同井壁厚度受力情况

按照上一节的计算思路，对内径为20m的立井进行受力计算，其立井井壁厚度分别为：1m、1.5m、2.0m、2.5m。通过对立井四方面受力情况的计算，其计算结果汇总至表3：

表3 内径20m的立井井壁厚度受力表

续表3 内径20m的立井井壁厚度受力表

按照本次研究的地下停车场立井采用混凝土强度为C70，安全系数为2.0的工程标准，因此在井深为200m，内径20m的条件下，井壁厚度以0.1m的递增趋势按照以上计算，要满足地下停车场工程修建标准，即最大应力为35Mpa时，立井井壁的厚度为2.7m。经计算，井壁厚度为2.7m时，作用在立井上的各方向应力数值结果如下：

此时，

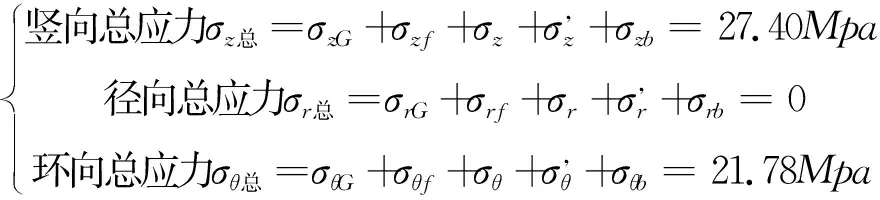
经校核，满足库伦-纳达尔准则。

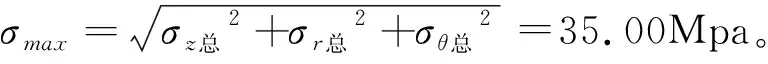
3 内径15m及20m的立井井壁厚度设计说明

以深200m地下停车场施工方案为标准，当具体工程参数如下时：井壁混凝土强度等级σc= 70MPa，σt= 4.5 MPa；钢筋混凝土体积密度ρc=2 500 kg/m 3，弹性模量 E=37GPa，泊松比μ=0.18，热膨胀系数 αf=10×10-61/℃，内井壁温度30 ℃，外井壁温度17 ℃，To=-10℃，Ta=30 ℃-(-10℃) =40℃，Tb=17℃- (-10℃)=27℃，表土密度γe=1 900 kg/m3，静摩擦系数 k0=0.3，侧压系数λ=0.333，基床系数k=40×106N/m3。求得安全系数为2.0及3.0下的立井井壁厚度标准，结果见下表4，表5。

表4 安全系数2.0时，立井井壁厚度设计方案

表5 安全系数3.0时，立井井壁厚度设计方案

4 结论

本文研究了内径分别为15m和20m的立井不同井壁厚度下的立井应力荷载，具体分析从1.0m-3.0m的立井井壁受力情况，得出的结论如下：

(1)采用混凝土强度为C70，安全系数为2.0的地下停车场立井工程设计时，内径为15m的立井最佳壁厚为0.5m，内径为20m的立井最佳壁厚2.5m，井壁底端内壁最高应力为35Mpa。

(2)安全系数为2.0，混凝土强度为C70，考虑竖向摩擦力的影响时，内径15m的立井最佳壁厚2.5m，内径20m的立井最佳壁厚2.7m，井壁底端内壁最高应力为35Mpa。

(3)工程采用混凝土强度为C70，安全系数为3.0时，由于考虑竖向摩擦力的影响，立井最大应力均超过了井壁底端内壁最高应力23.3Mpa，因此无论内径为15m或者20m，都无法得出结果。

(4)在不考虑竖向摩擦力的情况下，安全系数为3.0的工程设计，内径为15m的立井，最佳壁厚为1.70m，内径20m的立井，最佳壁厚为2.00米。