高压下β-InSe弹性常数、电子结构的第一性原理研究

龚铁夫， 宋述鹏， 刘俊男 ， 吴 润

(1. 武汉科技大学省部共建耐火材料与冶金国家重点实验室， 武汉 430081; 2. 武汉科技大学材料与冶金学院， 武汉 430081)

1 引 言

近年来，层状过渡金属硫化物半导体，如MoS2[1]、MoSe2[2]、WS2[3]以及WSe2[4]等，由于奇特的物理光电性质而引起广泛的关注. InSe属于层状III - VI族金属硫化物半导体，其具有优异的电子和光学性质， Sucharitakul[5]等人发现在室温下InSe的电子迁移率可以达到103cm2V-1s-1，在液氦温度下可以达到104cm2V-1s-1. 此外，InSe具有很多重要的物理性质，如较高的载流子迁移率、量子霍尔效应以及优异的光学响应，可以应用于聚合物肖特基二极管、微电池、电容器、红外器件以及异质结器件的制备[6]. InSe可以由多种沉积技术制备得到，Bridgman-Stockbarger技术是制备InSe最常用的一种方法，制备得到的主要为γ-或者ε-InSe[7]，此外，也有人用化学气相沉积法制备得到β-InSe[8].

Errandonea[9]通过实验研究发现，单斜相InSe在高压下结构的对称性会发生变化，并且会在19.4±0.5 GPa压力下相变为四方相(I4/mmm)，InSe在高温高压下也会表现出类似金属的特性. Li等[3]通过第一性原理计算发现，在20 GPa时下WS2的带隙会由0.843 eV减小为0 eV，即WS2发生了由半导体转变为半金属的相变. Li等[4]通过第一性原理计算发现，WSe2在40 GPa时会发生半导体到半金属的相变. Kosobutsky[10]通过第一性原理计算，研究了单轴和双轴压力对层状GaSe结构、弹性和电子性质的影响，发现在约10 GPa单轴压力下GaSe可能会发生向金属型的转变.

β-InSe是典型的二维层状硒化物，但目前关于β-InSe在高压下的理论计算研究较少，因此本文采用第一性原理计算，研究β-InSe晶体结构在高压下弹性常数、机械性能和电子结构的变化，以期对于层状InSe电子材料和光学器件的制备提供理论支持.

2 计算方法和模型

本文基于密度泛函理论，采用Materials Studio中的CASTEP量子力学模块进行计算，采用广义梯度近似(Generalized Gradient Approximation, GGA)，电子关联为PBE泛函，平面波截断能(Cutoff Energy)取450 eV，采用Monkhorst-Pack方法划分K点网格，网格选取为5×5×2. 对β-InSe在0～20 GPa高压下进行了几何优化和性质计算，利用超软赝势(Ultrosoft)来模拟价电子和离子实之间的相互作用，采用Gimme方法来修正层间范德华力的影响[4]，β-InSe参与计算的价电子为：In(4d105s25p1)、Se(4s24p4). 在SCF中，自洽迭代收敛总能量优于5.0×10-7eV/atom，采用BFGS(Broyden-Fletcher-Goldfarb-Shanno)算法使得0～20 GPa下体系总能量和内应力最小，几何优化时收敛精度(Convergence tolerance)设置如下：收敛总能量优于1.0×10-5eV/atom，离子最大Hellmann-Feynman力优于0.03 eV/Å，最大应力优于0.05 GPa，离子最大位移优于0.001 Å，在加压计算中，采用Pulay Mixing方法进行修正，几何优化、弹性常数及电子结构计算设置的参数保持一致.

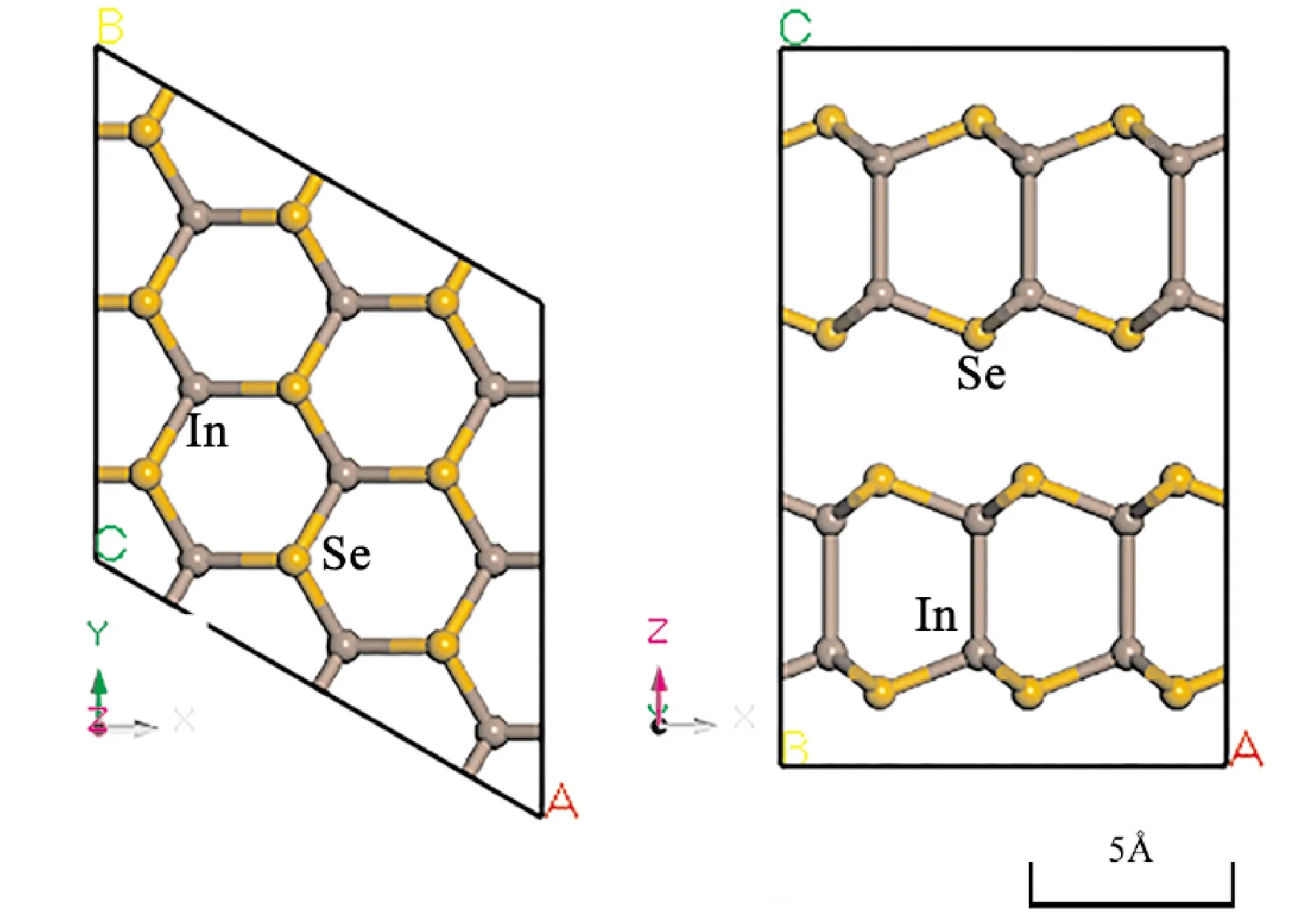
图1 β-InSe 3×3超胞的晶体结构Fig. 1 Crystal structure of β-InSe 3×3 super-cells

3 结果与讨论

3.1 晶格参数

表1β-InSe晶格参数以及In-In和In-Se键长

Table 1 Lattice constants ofβ-InSe and the bond length of In-In, In-Se

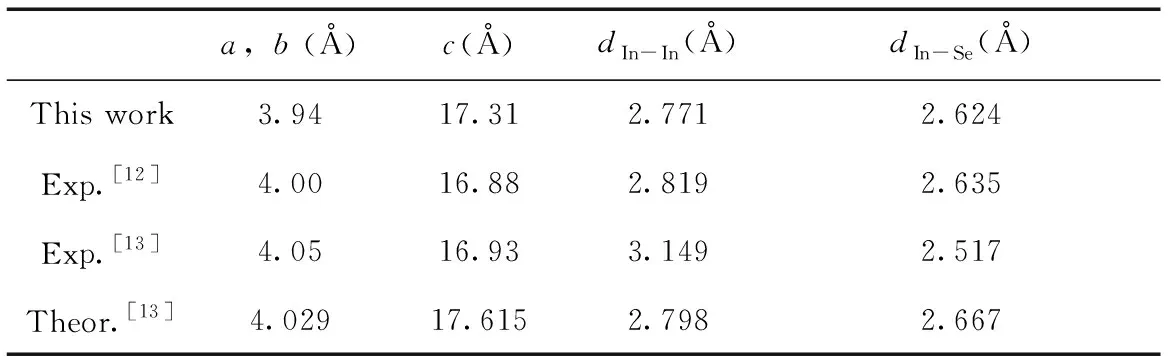
a,b (Å)c(Å)dIn-In(Å)dIn-Se(Å)This work3.9417.312.7712.624Exp.[12]4.0016.882.8192.635Exp.[13]4.0516.933.1492.517Theor.[13]4.02917.6152.7982.667

表2是β-InSe在0～20 GPa下晶格常数变化情况. 随着压力的增大，晶格常数、晶胞体积逐渐减小. 同时，c/a的相对变化率均不大于4.14%，说明其整体结构并未发生大的畸变，晶胞仍保持稳定. 此外，β-InSe在0～20 GPa下的原子之间距离d随着压力增大而逐渐减小，dIn-In和dIn-Se变化率分别为6.7%和4.3%.

表2 计算得到β-InSe在0～20GPa下的结构参数

Table 2 Structural parameters ofβ-InSe as a function of pressure (0～20GPa)

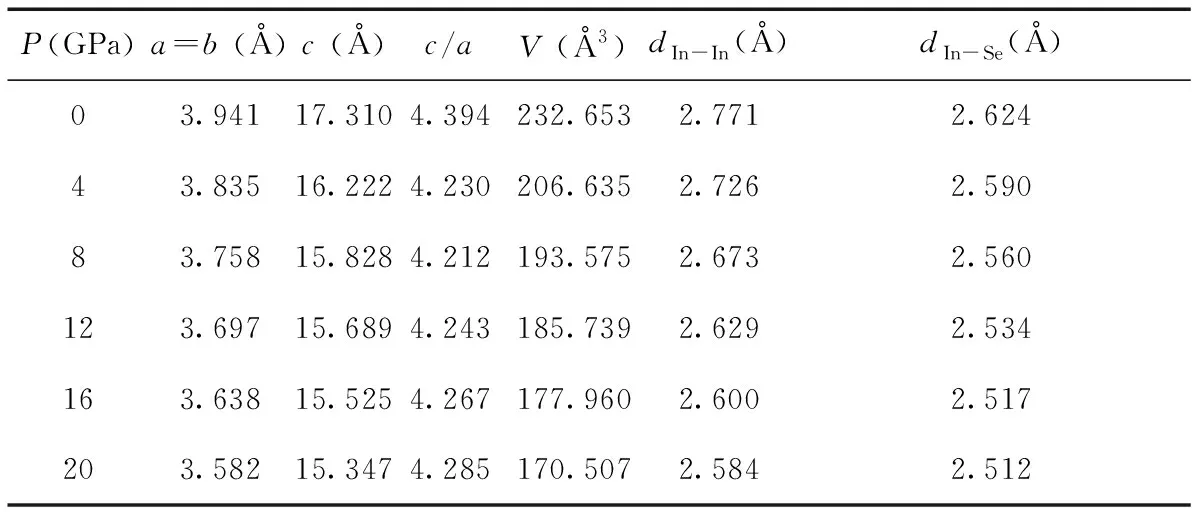
P(GPa)a=b (Å)c (Å)c/aV (Å3)dIn-In(Å)dIn-Se(Å)03.94117.3104.394232.6532.7712.62443.83516.2224.230206.6352.7262.59083.75815.8284.212193.5752.6732.560123.69715.6894.243185.7392.6292.534163.63815.5254.267177.9602.6002.517203.58215.3474.285170.5072.5842.512

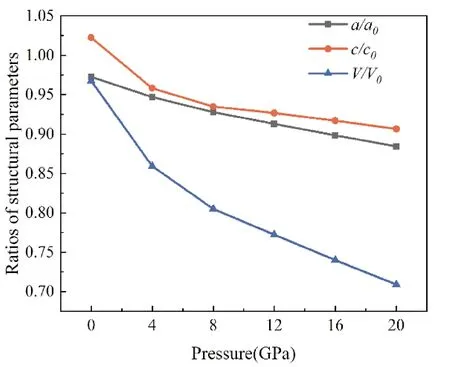
图2 β-InSe在0～20 GPa下的归一化晶格参数a/a0、c/c0、V/V0Fig. 2 Normalized structural parameters a/a0, c/c0, V/V0 of β-InSe under the pressure of 0～20 GPa

图2为β-InSe归一化的晶格参数a/a0、c/c0、V/V0随压力的变化曲线(其中a0、c0和V0是实验测得的β-InSe结构参数(ICSD#30377))，可以看到a/a0、c/c0和V/V0随着压力增大逐渐减小，而且折线均趋于平缓，这是由于随着晶格参数的减小，β-InSe原子距离和层间距离减小，斥力不断增大，表现为抗压缩能力增强，从图中也可知在0～20 GPa范围内，β-InSe晶体结构比较稳定.

3.2 高压下弹性常数推导β-InSe力学性能以及机械稳定性

已经有实验研究表明，β-InSe在高压和中等温度下会发生相变[14]，为了研究β-InSe在高压下的力学性能及机械稳定性，本文采用应力-应变法计算得到β-InSe在0～20 GPa下的弹性常数，通过弹性常数推测β-InSe在高压下的力学性能和机械稳定性.

对于β-InSe这种类石墨烯结构的层状材料，通过弹性常数可以分析β-InSe固态晶体结构在各个方向的受力情况，而且德拜温度、热膨胀系数以及格林艾森参数等热力学参数也可以由弹性常数导出，弹性常数Cijkl的表达式为[15]：

(1)

其中ekl，sij，X，x分别为欧拉应变张量，外加应力张量，变形前后的坐标.

β-InSe由于是斜面六方晶体结构，所以具有五个独立的弹性常数，分别为C11，C33，C44，C12和C13. 对于六方晶系而言，在高压下的机械稳定性可以通过以下条件来判断[16]：

(2)

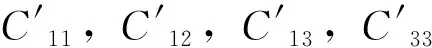
(3)

通过以上五个独立的弹性常数可以得到弹性模量，Voigt和Reuss两种近似方法可以计算得到弹性模量. 对于六方晶系来说，Voigt(BV)和Reuss(BR)计算体积模量的公式如下：

(4)

同样地，六方晶系计算剪切模量的公式如下：

(5)

在Voigt-Reuss-Hill(VRH)近似方法中，体模量(B)和剪切模量(G)近似看作Voigt和Reuss值的算术平均数，公式如下：

(6)

杨氏模量(E)和泊松比(v)通过体积模量和剪切模量计算得到，公式如下：

(7)

考虑到β-InSe的弹性弹性常数C11和C33分别代表该结构在a和c方向上抵抗塑性变形能力的大小，C44代表在轴向上抵抗剪切应变能力的大小. 图3给出β-InSe在0～20 GPa下弹性常数随压力增加的变化曲线，0～12 GPa时，随着压力增大，C11、C12、C13、C44单调增大，C33在4 GPa时突然减小，可能是由于β-InSe在c轴方向上受压力影响更明显[4]；此外，C11、C12、C13、C33、C44在16 GPa时突然大幅减小，其中C11、C33、C44分别减小了56.7%、48.4%、57.2%.

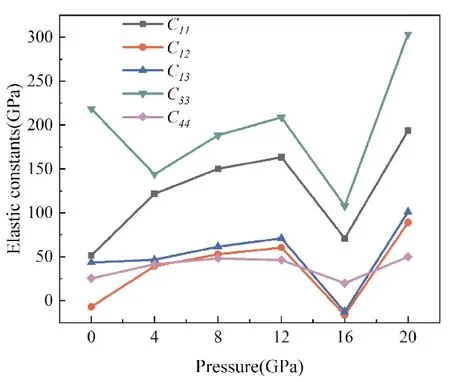
图3 β-InSe在0～20GPa下的弹性常数Fig. 3 Elastic constants of β-InSe under the pressure of 0～20GPa

基于得到的五个独立的弹性常数，再根据Voigt-Reuss-Hill(VRH)近似方法，得到β-InSe在0～20 GPa压力下的体积模量、剪切模量、杨氏模量和泊松比随压力变化的规律. 如图4所示，0～12 GPa时，β-InSe晶体结构杨氏模量(E)和体积模量(B)随着压力增大而增大，其抵抗横向变形以及抵抗断裂的能力均随着压力增大而增大. 然后G、E、B、v在16 GPa时突然大幅减小，且G、E、B分别减小了34.9%、53.3%、82.9% ，其中B值变化幅度最大.G、E、B下降表明在16 GPa时β-InSe较容易发生形变.

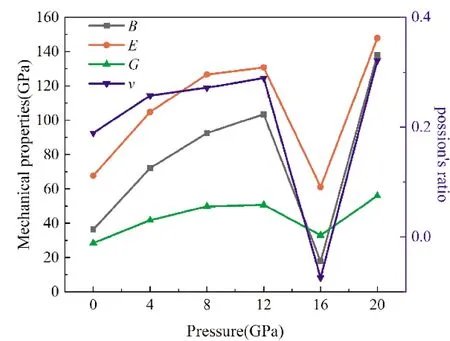
图4 β-InSe在0～20 GPa压力下的体积模量B、剪切模量G、杨氏模量E和泊松比vFig. 4 Bulk modulus, Shear modulus, Young’s modulus and Poisson’s ratio of β-InSe under the pressure of 0～20 GPa

3.3 电子结构

图5所示为0、8、20 GPa下β-InSe沿着高对称性方向计算得到的能带结构. Bandurin[5]等人通过光致发光光谱发现β-InSe的带隙会随着层数的减少而增大，多层InSe转变为双层InSe，其带隙值增大了0.5 eV.

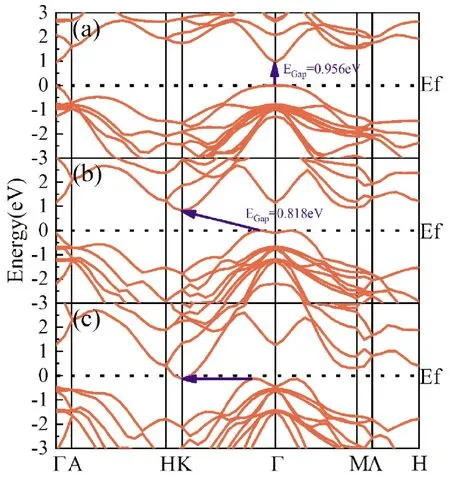
图5 β-InSe在0 GPa(a)、8 GPa(b)和20 GPa(c)时的能带结构图Fig. 5 Band structures of β-InSe at (a) 0 GPa, (b) 8 GPa and (c) 20 GPa

图5(a)中价带顶(VBM)和导带底(CBM)都落在Γ点，表明β-InSe在0 GPa是直接带隙半导体，带隙EG=0.956 eV，这接近于实验值的0.93 eV[17]. 如图5(b)所示，由于4 GPa时带隙是0.988 eV，因此随着压力增大，β-InSe的带隙值先增大后减小，在8 GPa时VBM落在Γ和K点之间，CBM则落在K点，EG=0.818 eV，此时β-InSe由直接带隙半导体转变为间接带隙半导体，这与Errandonea等人的计算结果一致[9]. 如图5(c)所示，随着压力增大，带隙由于能带扩展，间接带隙逐渐变小，压力增大到20 GPa时部分导带底已经越过费米能级，EG=0 eV，表明此时β-InSe可能发生了半导体向半金属的相变[4]. 同时，比较前文中弹性常数的计算结果可以推测，β-InSe在20 GPa时其力学性能也随之发生变化.

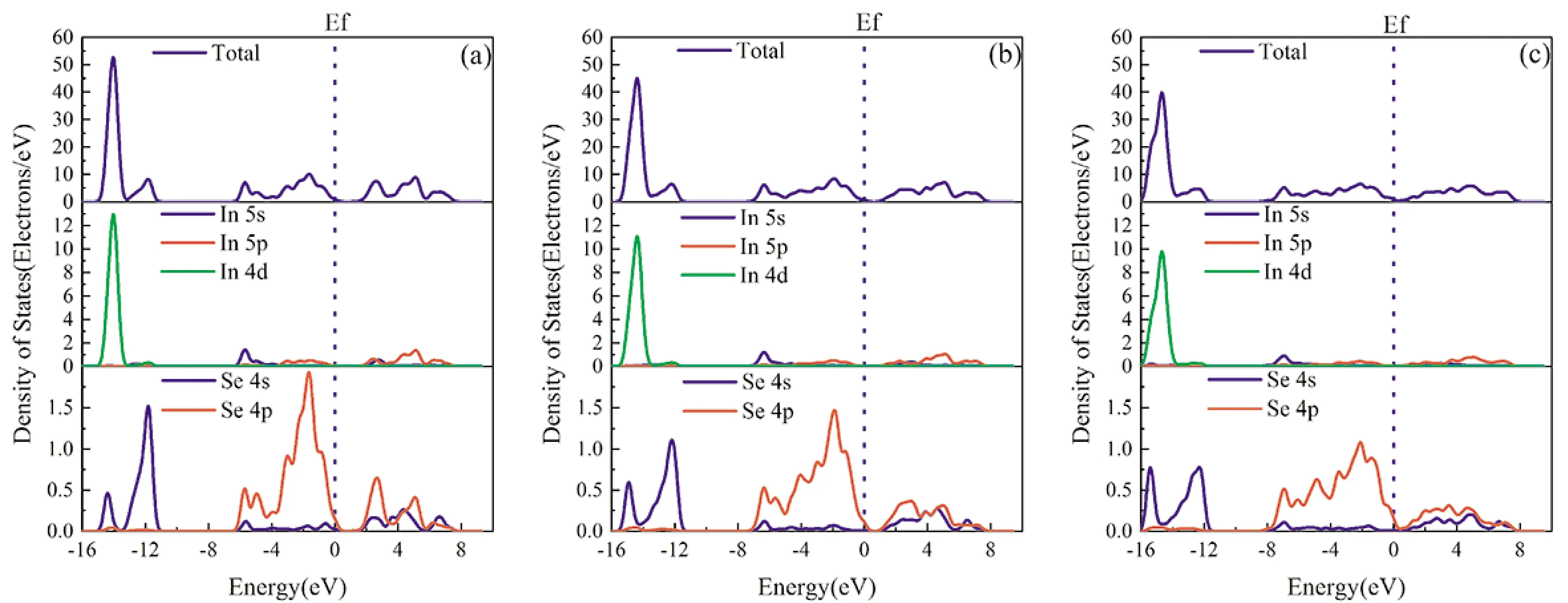
图6 β-InSe在0 GPa(a)、8 GPa(b)和20 GPa(c)时的总态密度和局部态密度图Fig. 6 TDOSs and PDOSs of β-InSe at (a) 0 GPa, (b) 8 GPa and (c) 20 GPa

图6给出了β-InSe在0、8、20 GPa下的总态密度(TDOS)和局部态密度(PDOS).β-InSe在0 GPa时的态密度和局部态密度如图6(a)所示，从-15.17 eV到-13.18 eV，峰宽为1.99 eV，主要由Se4s和In4d态组成；从-13.18 eV到-10.95 eV，峰宽为2.23 eV，主要由Se4s态贡献；从-6.53 eV到-4.32 eV，峰宽为2.21 eV，主要是Se4p和In5s态杂化引起的；从-4.32 eV到0 eV，峰宽为4.32 eV，主要由Se4p态组成；从0 eV到3.35 eV，峰宽为3.35 eV，由Se4s、4p态和In5s、5p态分别杂化引起的；从3.35 eV到7.86 eV，峰宽为4.51 eV，主要由In5p态和Se4s、4p态分别杂化引起的，由此可以推断出In-In和In-Se之间存在共价键[12]. 如图6(b)和6(c)所示，首先，β-InSe的TDOS和PDOS值在其分布的整个范围内逐渐减小；其次，价带逐渐变宽，底部价带略微移动到较低的能量范围；在临近费米能级处，随着压力增大，In5p和Se4s和Se4p轨道杂化程度增大，β-InSe的带隙消失，转变为半金属相. 由此推测，β-InSe在高压下由半导体转变为半金属相归因于In-Se共价键增强而非层间范德华力的作用[18].

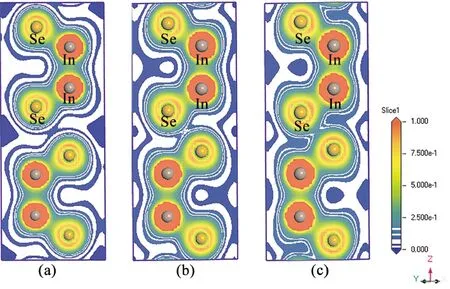
图7 β-InSe在0 GPa(a)、8 GPa(b)和20 GPa(c)时的电荷密度分布图Fig. 7 Charge density distributions of β-InSe at (a) 0 GPa, (b) 8 GPa and (c) 20 GPa

图7(a)所示，0 GPa时Se-In和In-In原子之间是由共价键连接，而Se-In-In-Se的片层之间不存在化学键，只存在范德华相互作用[4]. 随着压力增大，Se-In和In-In原子之间的电荷密度增大，表明Se-In和In-In原子之间的共价键增强；而且随着压力增大，Se-In-In-Se片层间距减小，两个片层之间的Se-Se原子之间电荷分布密度逐渐增大，可能是由于片层间距减小，导致Se-Se原子对之间也开始产生共价键，导致层与层之间相互作用增强.

4 结 论

本文基于密度泛函理论，采用第一性原理计算方法研究β-InSe在0～20 GPa高压下的晶体结构、弹性常数、机械性能和电子结构.

(1)在0～20 GPa范围内，随着压力的增大，β-InSe的晶格常数、晶胞体积逐渐减小，结构参数a/a0、c/c0、V/V0单调减小，c/a相对变化率均不大于4.14%，其晶胞整体保持稳定并未发生大的畸变.

(2)在0～20 GPa范围内，G、E、B、v随着压力增大而增大，在16 GPa时大幅减小，G、E、B分别减小了34.9%、53.3%、82.9%，其中B值变化幅度最大.

(3)β-InSe在0 GPa时为直接带隙半导体. 随着压力增大，8 GPa时开始发生向间接带隙半导体的转变，20 GPa时带隙消失，β-InSe发生由半导体向半金属的相变.

(4)在0～20 GPa范围内，随着压力增大，Se-In和In-In原子之间的电荷密度增大，Se-In和In-In原子之间的共价键增强，Se-In-In-Se层间距离减小.