基于片烟图像处理面积及feret直径的分形分析

李 晓，袁 帅，姚二民，赵凯歌，王 巍，姚光明

1. 郑州轻工业大学，郑州高新技术开发区科学大道136 号 450001

2. 中国烟草总公司郑州烟草研究院，郑州高新技术产业开发区枫杨街2 号 450001

片烟结构是衡量打叶质量的重要指标，同时也决定了烟丝结构，而烟丝结构又影响卷烟卷制质量[1-2]。目前片烟结构的评定依据为片烟面积，主要依赖于“叶片振动筛”离线检测法[3]，且该方法存在过筛、漏筛、对片烟损伤大等缺点，不仅费时费力、准确率低，而且检测过程滞后于控制过程[4-5]，不能准确反映批次片烟结构的真实情况，很难满足现代化卷烟生产工艺的要求。图像处理技术凭借再现性好、处理精度高、适用面宽、灵活性高、信号便于传输等优点[6]，在烟草行业得到了广泛应用[7-13]。徐大勇等[14]利用数字图像分析法通过测定片烟面积来表征片烟结构，在片烟面积大于817.95 mm2时检测误差小于1%，片烟面积小于361.00 mm2时，检测误差小于4%。但片烟结构具有多样性，如面积相同而长度差距较大的片烟，两者结构差异较大，仅通过面积这个单一指标仍不能反映出片烟之间结构的具体差异。分形维数作为研究分形的重要参数，可有效度量图像的几何特性与复杂性，揭示隐藏在复杂现象背后的规律以及局部和整体之间的本质联系[15]。将分形维数与片烟面积和feret 直径两个特征参数相结合，能够分析片烟之间的差异性，进而对片烟结构作出更为具体的描述。为此，利用图像处理技术从宏观角度对片烟的分形特性进行分析，通过分形理论对片烟面积及feret 直径进行定量研究，构建片烟面积、feret 直径与片烟分形特性之间的关系，旨在为片烟结构的评定提供一种更为准确、全面、客观的新方法，为片烟结构的在线检测提供技术支持。

1 材料与方法

1.1 材料与仪器

打叶复烤片烟（河南中烟工业有限责任公司）。

CV-035C 彩色线阵CCD 相机（有效像素32 万，像素传输频率24.5 MHz）、CA-LS6 型广角镜头（焦距1.4～8.0 mm）、KV-1000 型PLC（日本Keyence 公司）；SL-VL14728-W 型光源（波长范围380～780 nm，广东奥普特科技股份有限公司）；Image-Pro Plus 6.0 图像分析软件（美国Media Cybernetics 公司）；TQ-2 型片烟振动分选筛（中国烟草总公司郑州烟草研究院）；PL203 电子天平（感量0.001 g，瑞士Mettle-Toledo 公司）。

1.2 方法

1.2.1 片烟样品的获取

将各种片形的片烟样品置于温度（22±1）℃、相对湿度（60±2）%的环境中平衡48 h[16]。利用片烟振动分选筛对片烟样品进行筛分（筛网孔径：25.4、12.7、6.35 mm），计算各层筛网上片烟样品数量及所占比例，根据所占比例从每层筛网上取定量片烟样品，共抽取片烟样品100 片。

1.2.2 片烟图像的采集及分割

将100 片片烟样品依次无折叠地平铺于CCD相机测量区域，采集片烟样品的图像信息并保存。运用Matlab 软件对采集的片烟图像进行灰度化处理和滤波增强，利用Otsu 算法对图像进行分割。该方法的基本原理是以最佳阈值将图像的灰度值分割成两部分，使目标与背景之间的方差最大，既具有最大分离性。设图像包含L 个灰度级（0,1…,L-1），灰度值为i 的像素点数为Ni，若灰度级所包含所有的像素个数为M×N，则灰度值为i 的点的概率为：

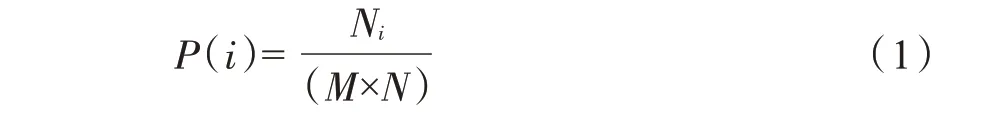
分割前后的片烟图像如图1 所示。可以看出，基于Otsu 算法的片烟图像分割效果理想，符合片烟的原始形态。

图1 片烟原始图像及分割后图像Fig.1 Original image and segmented image of strip

1.2.3 片烟参数的测量

将片烟二值图像载入IPP（Image-Pro Plus）图像处理软件中，使用Count and measure object（计算测量对象）自动识别跟踪对象。并对IPP 图像处理软件中的测量系统进行标尺设定，设定后测量系统中数字图像的单个像素点长度为3.20 mm、面积为10.24 mm2。由于图片分析测量的几何数值单位是像素，标定测量系统建立图像中像素与实际空间尺度数据之间的关系[17]，即可测得片烟的实际面积与feret 直径[18]。为保证测量的准确性，每次均在标定后的相同环境下测量。

1.2.4 片烟外形轮廓曲线提取

为获取片烟外形轮廓曲线，运用matlab 中的bwperim 函数对片烟的二值图像进行处理，获取轮廓曲线，然后将获得的二维图像用photoshop cs6软件进行处理，再现出整个片烟外形轮廓曲线的虚拟二维图像，如图2 所示。

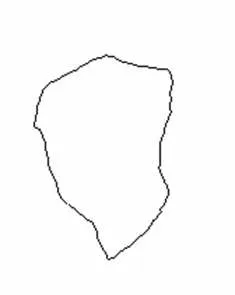
图2 片烟轮廓曲线图像Fig.2 Contour curve image of strip

1.2.5 片烟分形维数计算方法

对于具有自相性特征的目标可利用分形理论进行分析[19-20]。片烟形状不规则且具有自相似特征，故可利用分形几何法描述片烟结构及形状。片烟分形维数的计算方法采用改进的计盒维数法（box-counting dimension）[21-22]，即用正方形覆盖片烟轮廓曲线的虚拟图像，用边长为1/2 的测量尺度c进行分割，计算方格与片烟轮廓曲线相交的网格数（即盒子数），记为N（c）；将正方形边长继续分割5 次，使正方形边长达到极小，其测量尺度c 分别为：1/4、1/8、1/16、1/32、1/64，并计算出不同测量尺度下的网格数N（c），如图3 所示。因N∝A·C-D，将两边同时取对数得：

由公式（2）可得：

式中：D—片烟轮廓曲线分形维数；A—大于零的任意常数。

以InN 为Y 轴、In（1/c）为X 轴，应用SPSS 12.0对x 和y 进行直线线性回归分析，线性回归方程的斜率为片烟的分形维数D。

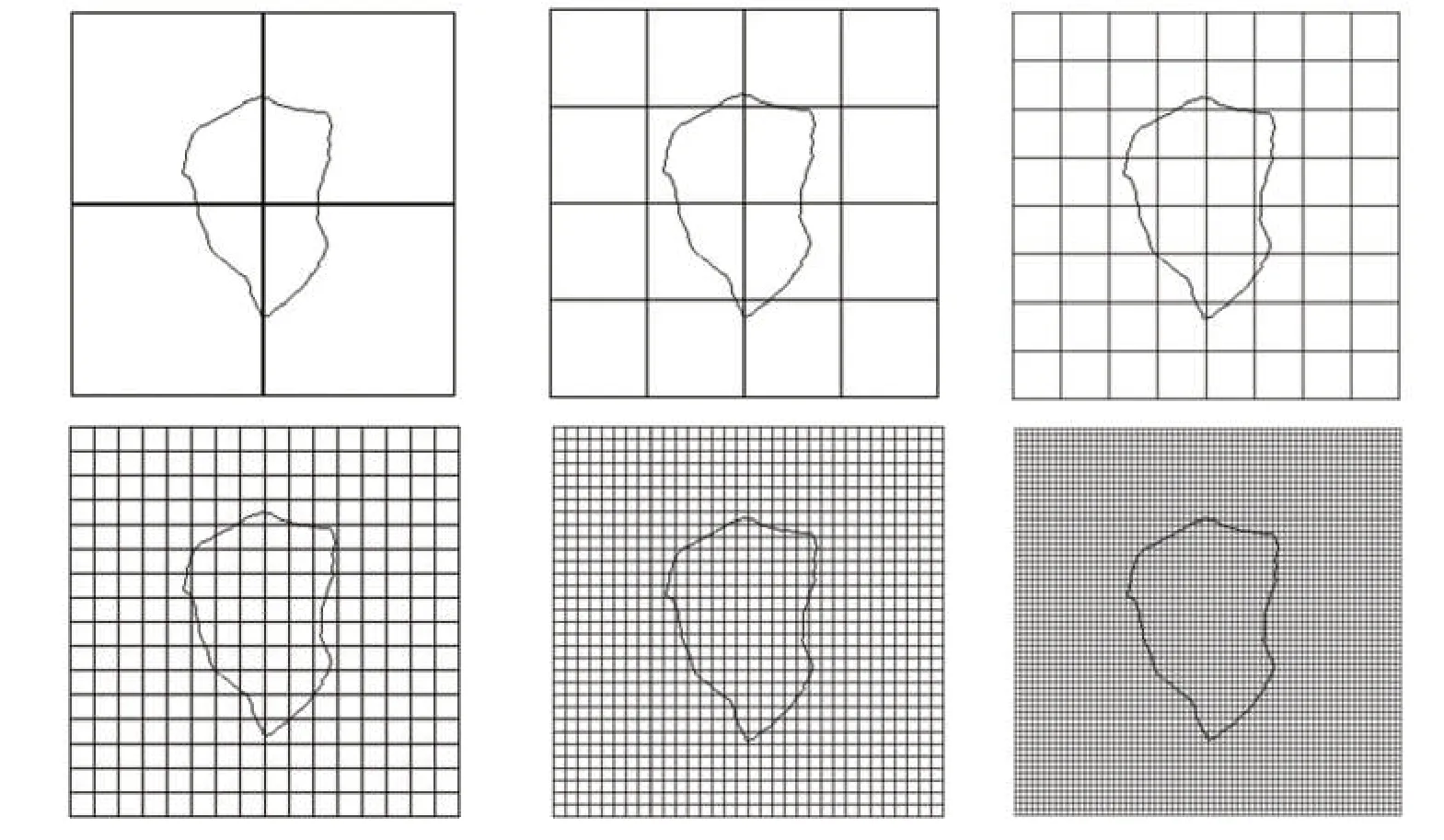
图3 分形计盒维数示意图Fig.3 Schematic diagram of fractal counting box dimension

2 结果与分析

2.1 片烟参数测量的准确性分析

为检验片烟面积测量的准确性，制作边长1～8 cm 的正方形样片。根据1.2.3 节的方法分别对8个正方形样片的面积进行测定，测定结果与正方形样片的标准面积进行配对样本T检验分析，结果见表1。

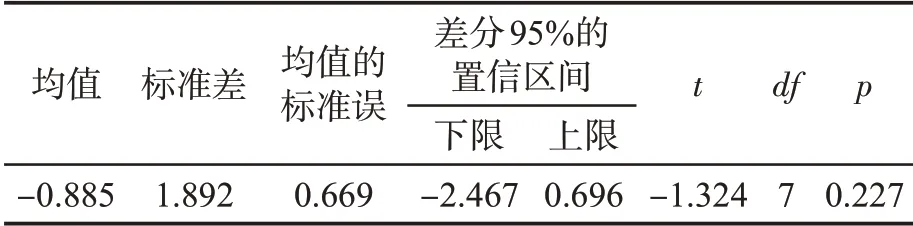
表1 配对样本T 检验结果①Tab.1 T-test results of paired samples

2.2 片烟分形维数的分析

根据1.2.5 节方法，对片烟样品进行试验分析，计算出不同测量尺度c 下的盒子数N（c），取其对数InN 与In（1/c），分别以In（1/c）为自变量，InN 为因变量进行回归分析，结果见表2。

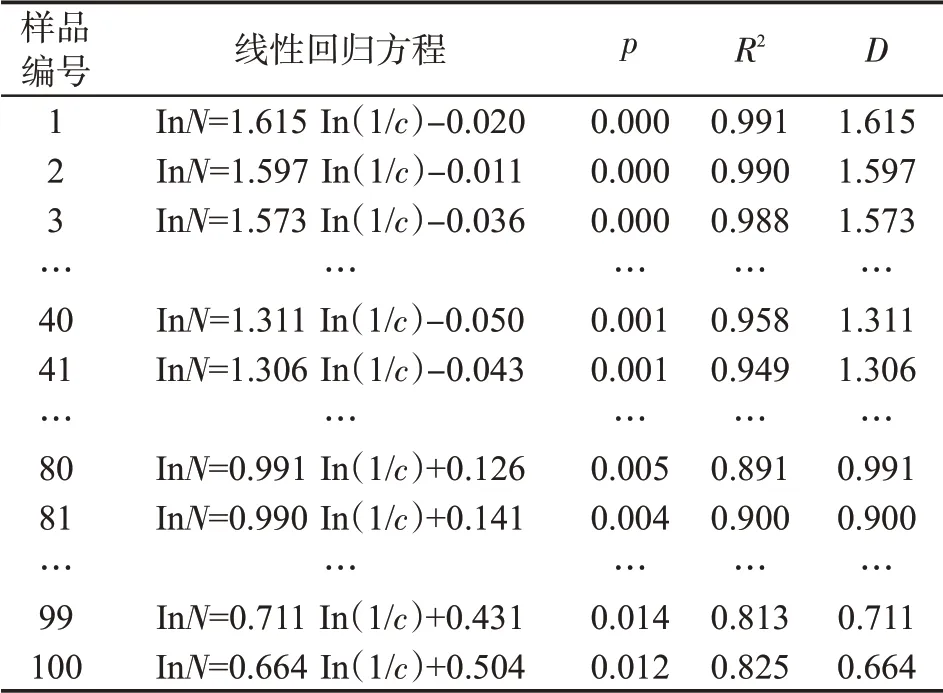
表2 片烟分形维数Tab.2 Fractal dimension of strips

由表2 可知，p 值均小于0.05，表示所拟合的回归方程均显著。R2均大于0.8，说明各方程拟合效果较好。因此，通过计盒维数法运用In（1/c）和InN 的线性回归系数来表征片烟的分形维数是合理的，且所测得片烟样品的分形维数范围为0.664～1.615。

2.3 片烟分形维数模型的建立及验证

2.3.1 片烟分形维数与片烟面积、feret 直径的简单相关分析

由表3 可知，片烟分形维数与片烟面积、feret直径均呈极显著正相关，且片烟面积与分形维数的相关性大于feret 直径与分形维数的相关性。片烟面积与feret 直径也呈极显著正相关。

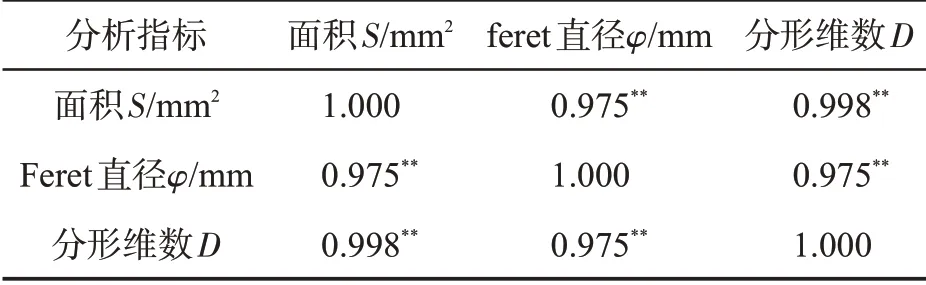
表3 片烟分形维数与面积、feret 直径的简单相关性Tab.3 Simple correlation between fractal dimension and area, feret's diameter of strips

2.3.2 片烟分形维数与片烟面积、feret 直径的线性回归分析

分别以片烟面积S、feret 直径φ 的自然对数lnS、lnφ为自变量，以分形维数D 为因变量，采用origin9.0 软件对其进行线性回归，探究片烟面积S、feret直径φ与片烟分形维数D的关系，结果见图4。

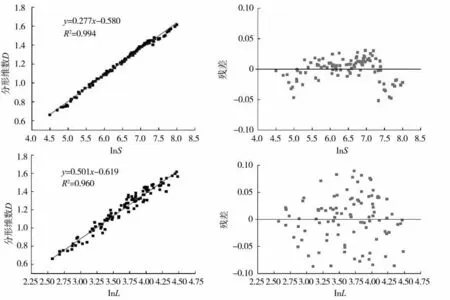
图4 线性拟合方程及残差图Fig.4 Linear fitting equation and residual graph

由图4 可知，lnS、lnφ与分形维数D 所拟合方程的R2均大于0.95，残差均在±0.1 以内，表明残差符合无偏性假设，该方程拟合效果良好，可靠性高。lnS 与分形维数D 的拟合效果优于lnφ与分形维数D 的拟合效果，表明片烟分形维数D 与片烟面积S 的关系较与feret 直径φ的关系密切。片烟分形维数D 与面积S、feret 直径φ的关系分别为D=0.277 lnS-0580、D=0.501 lnφ-0.619，由此可知对于片烟而言，随着片烟面积S、feret 直径φ的增加，其分形维数D 有所增加。

Thanksgiving falls on the fourth Thursday of November, a different date every year.The President must proclaim that date as the official celebration.

2.3.3 片烟分形维数模型的建立

为建立片烟分形维数模型，探究片烟分形维数D 与片烟面积S 及feret 直径φ之间的关系，根据所测片烟面积S、feret 直径φ与分形维数D 结果，利用Matlab 进行多项式拟合建立片烟分形维数模型，拟合方程为：

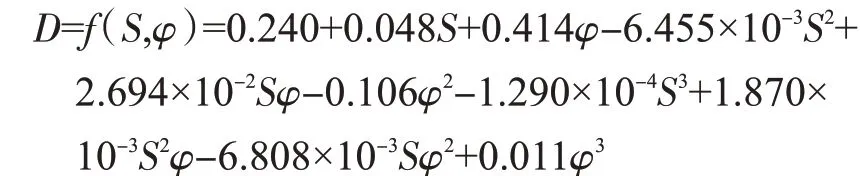
式 中：S 为 片 烟 面 积（cm2）；φ 为feret 直 径（cm）。拟合方程均方根误差RMSE 为0.016、误差平方和SSE 为0.025，决定系数R2达0.996，说明所建方程水平显著，且拟合度良好，其模型如图5所示。

图5 片烟分形维数模型Fig.5 Fractal dimension model for strips

2.3.4 片烟分形维数模型的验证

为验证片烟分形维数模型的准确性，随机抽取片烟样品35 片，将其置于所建模型中计算片烟样品分形维数预测值，并利用计盒维数法测得片烟样品分形维数的实测值，对片烟样品分形维数的预测值及实测值进行分析，如图6 所示。

图6 可见，片烟样品分形维数预测值和实际值的变化趋势基本相同，绝对误差与相对误差很小，绝对误差最大值为0.038，最小值为8.542×10-4，平均值为0.014；相对误差最大值为2.9%，最小值0.007%，平均值为1.130%。结果表明误差均在允许范围内，也说明所建立的片烟分形维数模型能够对片烟分形维数作出准确预测。

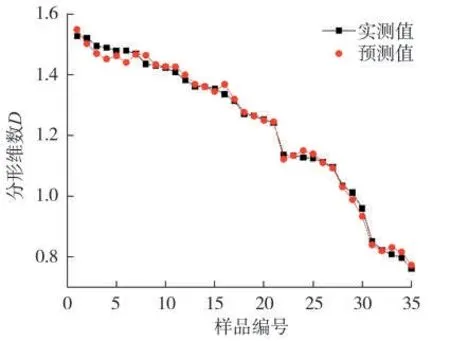
图6 片烟样品分形维数预测值和实测值Fig.6 Predicted values and measured values of fractal dimension of strips

2.4 片烟结构的定量表征

2.4.1 片烟结构外观区域模型的划分

根据《卷烟工艺规范》中对大中小片划分的标准，将其折合为片烟面积时即大片＞6.452 cm2、中片1.613～6.452 cm2、小片0.403～1.613 cm2，将片烟样品按面积划分为Ⅰ、Ⅱ、Ⅲ3 个区域，如图7 所示，各区域之内片烟面积差异较小，而区域之间片烟面积差异较大；并将该组片烟样品按feret 直径划分为A、B、C 3 个区域，如图8 所示，片烟feret 直径由A 区域至C 区域发生显著变化且各区域之间片烟分形维数各不相同。

图7 片烟面积区域模型Fig.7 Regional model for strip area

结合片烟面积区域模型与feret 直径区域模型，将两者合并归纳构建片烟结构外观特征区域模型，如图9 所示。由图9 可知，同一区域内片烟面积与片烟feret 直径无明显变化且形态基本一致；对于相邻区域，ⅡB 与ⅡC 区域之间片烟feret直径变化较大，ⅡC 与ⅢC 之间片烟面积差异明显而feret 直径均大于25.4 mm；ⅠA、ⅡB、ⅢC 3 个区域之间，片烟面积及片烟feret 直径均发生显著性变化。

图8 片烟feret 直径区域模型Fig.8 Regional model for Feret's diameter of strips

图9 片烟结构外观特征区域模型Fig.9 Regional model for appearance characteristic of strip structure

2.4.2 片烟结构区域模型分形维数的划分

根据所测片烟样品的分形维数，统计图9 中各区域模型分别相对应片烟样品的分形维数数值，并进行归纳总结，如表4 所示。

表4 片烟结构区域模型分形维数范围Tab.4 Fractal dimension range of strip structure region model

为进一步对片烟结构作出更准确的描述，实现利用分形维数对片烟结构的定量表征，将片烟结构区域模型分形维数范围进行归类，如表5所示。

由表5 可知，将片烟结构划分为小片、中短片、中长片、大片4 种，且不同的片烟结构对应不同的分形维数，即片烟分形维数0.664＜D≤0.829 之间时，片烟为小片；片烟分形维数0.829＜D≤1.000时，片烟属于中片，但长度偏短，为中短片；片烟分形维数1.000＜D≤1.201 时，片烟属于中片，但长度偏长，为中长片；片烟分形维数1.201＜D≤1.615时，片烟为大片。

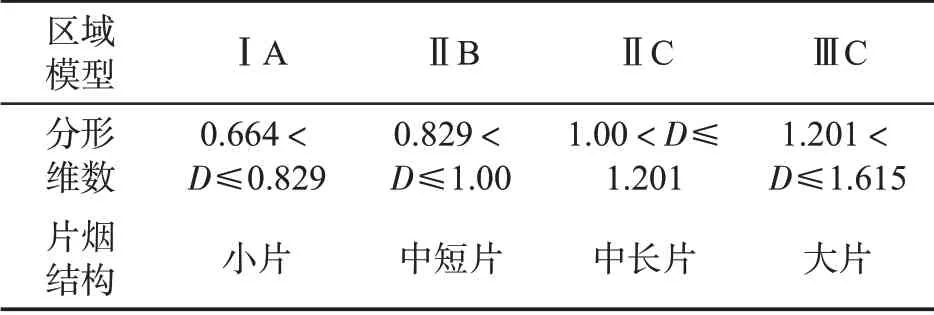
表5 片烟结构分形定量表征指标Tab.5 Fractal quantitative characterization index of strip structure

3 结论

（1）IPP 图像处理软件测量结果与正方形标准面积的T 检验p=0.227＞0.05，表明IPP 图像处理软件测量结果与正方形的标准面积无显著差异，利用IPP 图像处理软件技术可实现对片烟参数的准确测量。

（2）对运用计盒维数法测定片烟样品分形维数的结果进行分析可知，80%片烟样品的回归方程决定系数超过0.90，20%片烟样品的回归方程决定系数大于0.81，且方差分析结果P值均小于0.05，表明计盒维数法适用于片烟分形维数的测定。

（3）片烟面积S、feret 直径φ与片烟分形维数D均呈极显著正相关关系，且片烟分形维数D 与片烟面积S 的关系较与feret 直径φ的关系密切。根据片烟面积S及feret 直径φ对片烟分形维数D影响程度不同，建立了片烟分形维数模型，通过对片烟分形维数的实测值与预测值进行分析，实际值与预测值之间的绝对误差及相对误差均较小，表明所建片烟分形维数模型能够对片烟分形维数进行准确的测定。

（4）将片烟结构划分为小片、中短片、中长片、大片4 种，并运用分形理论对片烟结构做出定量的表征为：当片烟分形维数0.664＜D≤0.829 时，片烟为小片；片烟分形维数0.829＜D≤1.000 时，片烟为中短片；片烟分形维数1.000＜D≤1.201时，片烟为中长片；片烟分形维数1.201＜D≤1.615时，片烟为大片。