GROUND STATES FOR FRACTIONAL SCHR¨ODINGER EQUATIONS WITH ELECTROMAGNETIC FIELDS AND CRITICAL GROWTH∗
Quanqing LI(李全清)
Department of Mathematics,Honghe University,Mengzi 661100,China
E-mail:shili06171987@126.com
Wenbo WANG(王文波)
Department of Mathematics and Statistics,Yunnan University,Kunming 650091,China
E-mail:wenbowangmath@163.com
Kaimin TENG(腾凯民)†
Department of Mathematics,Taiyuan University of Technology,Taiyuan 030024,China
E-mail:tengkaimin2013@163.com
Xian WU(吴鲜)
Department of Mathematics,Yunman Normal University,Kunming 650092,China
E-mail:wuxian2042@163.com
Abstract In this article,we study the following fractional Schrödinger equation with electromagnetic fields and critical growthwhereis the fractional magnetic operator with 0
Key words fractional Schrödinger equation;fractional magnetic operator;critical growth
1 Introduction and Preliminaries
Consider the following fractional Schrödinger equation with electromagnetic fields and critical growth
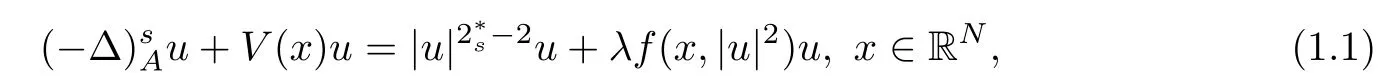
The fractional magnetic Laplacian is de fined by
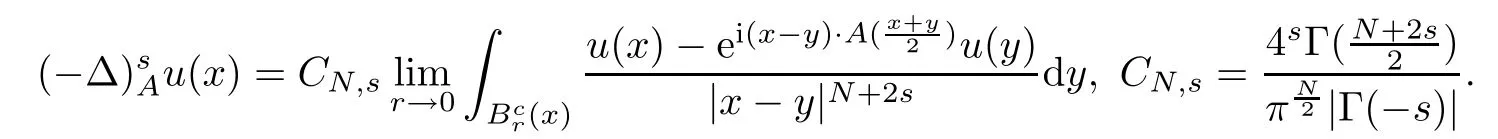
This nonlocal operator was de fined in[16]as a fractional extension(for any arbitrary s∈(0,1))of the magnetic pseudorelativistic operator,or Weyl pseudodifferential operator de fined with mid-point prescription[4].As stated in[30],up to correcting the operator by the factor(1−s),it follows thatu converges to−(∇u−iA)2u as s→ 1.Thus,up to normalization,the nonlocal case can be seen as an approximation of the local one.The motivation for its introduction is described in more detail in[16,30]and replies essentially on the L´evy-Khintchine formula for the generator of a general L´evy process.
The main driving force for the study of problem(1.1)arises in the following time-dependent Schrödinger equation when s=1,

where~is the Planck constant,m is the particle mass,A:RN→RNis the magnetic potential,P:RN→ RNis the electric potential,ρ is the nonlinear coupling,and ψ is the wave function representing the state of the particle.This equation arises in quantum mechanics and describes the dynamics of the particle in a non-relativistic setting[6,28].Clearly,the form ψ(x,t):=u(x)is a standing wave solution of(1.2)if and only if u(x)satis fies the following stationary equation

where ε=~,V(x)=2m(P(x)−E)and f=2mρ (see[9,14,15,18]).By applying variational methods and Ljusternick-Schnirelmann theory,Ambrosio and d’Avenia[4]proved the existence and multiplicity of solutions for the equation

when ε>0 small.Recently,Liang et al.in[23]obtained the existence and multiplicity of solutions for the fractional Schrödinger-Kirchho ffequation
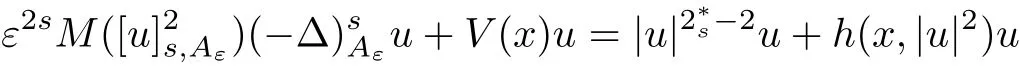
with the help of fractional version of the concentration compactness principle and variational methods.For other results concerning fractional magnetic Schrödinger equations one can also see[1,2].If the magnetic field A ≡ 0,then the operatorcan be reduced to the fractional Laplacian operator(−∆)s,which is de fined as
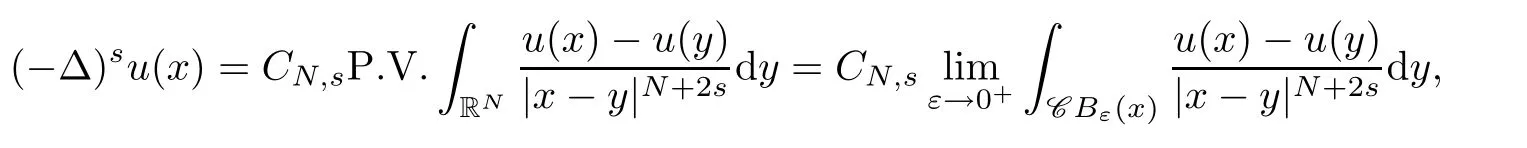

It is well known to us that the fractional Laplacian(−∆)scan be viewed as a pseudo-differential operator of symbol|ξ|2s,as stated in the following,refer to Lemma 1.1 in[27].Simultaneously,problem(1.1)becomes the fractional Schrödinger equation
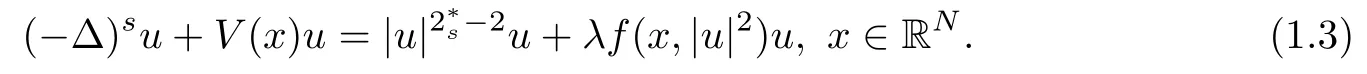
Solutions of equation(1.3)are standing wave solutions of the fractional Schrödinger equation of the form


which extends the results in[36],where Zhang et al.obtained the existence of ground states for subcritical problem
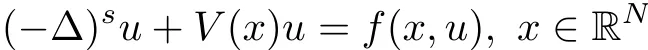
under the same periodic assumption of V and f.
Inspired by[26,36],in the present paper we focus our attention on the existence of ground states for critical problem(1.1)with electromagnetic fields.To our best knowledge,it seems that there is almost no work on the existence of solutions to equation(1.1)when V and f are asymptotically periodic in x.
Let H be the class of functions h∈ L∞(RN)such that,for every ε>0 the set{x∈ RN:|h(x)|≥ ε}has finite Lebesgue measure.In order to reduce the statements for main results,we list the assumptions as follows
(V1)V ∈L∞(RN)and V0:=V(x)>0.
(V2)There exists a function Vp∈ L∞(RN),which is 1-periodic in xi(i=1,···,N),such that V−Vp∈H and V(x)≤Vp(x)for all x∈RN.
(f1)f ∈ C(RN× R,R)and there exists 2 for all(x,t)∈RN×R,where C is a positive constant. (f2)f(x,t)=o(1)uniformly in x∈RNas|t|→0. (f3)tf(x,t)−F(x,t)≥stf(x,st)−F(x,st)for all(x,t)∈RN×R and s∈[0,1],where F(x,t):=f(x,τ)dτ. (f4)f(x,t)t>0 for all(x,t)∈RN×R{0}. (f5)There exists a function fp∈ C(RN× R,R),which is 1-periodic in xi(i=1,···,N),such that (i)|fp(x,t)|≤|f(x,t)|,∀(x,t)∈RN×R. (ii)|fp(x,t)− f(x,t)|≤ |h(x)|(1+|t|),∀(x,t)∈RN×R,where h∈H and q is given by(f1). (iii)tfp(x,t)−Fp(x,t)≥stfp(x,st)−Fp(x,st)for all(x,t)∈RN×R and s∈[0,1],where Fp(x,t):=Rfp(x,τ)dτ. (iv)fp(x,t)t≥0 for all(x,t)∈RN×R. Since{h∈L∞(RN):h(x)=0}⊂ H,the case+∞ >V∞:=≥ V(x)∈C(RN)veri fies assumption(V2).A simple example of fsatisfying hypotheses(f1)–(f5)is the function f(x,t)=|t|q2−2t and we may choose fp=f=|t|q2−2t in(f5).We point out that this kind of hypothesis(f3)was first introduced by Jeanjean in[19].Latter,it was used by Liu and Li[22]for the general case.Furthermore,it is easy to see that(f3)is weaker than the following assumption: For a function u:RN→C,set and Then let us introduce the Hilbert space endowed with the scalar product and where R(z)is the real part of the complex number z.By Lemma 3.5 in[16],we know that the embedding(RN,C)ô→ Lt(RN,C)is continuous for any t ∈ [2,]and the embedding with the norm In view of(V1)–(V2),the norms kuk andand kukAare equivalent.By condition(V1)we know that the embedding(RN,C)is continuous. For convenience,we replace(RN,R)with(RN)and de fine the homogeneous fractional Sobolev space Propositions 3.4 and 3.6 in[27]imply that where Hence we can de fine the norm on Hs(RN)as follows Moreover,the best fractional critical Sobolev constant is given by Our main result is the following. Theorem 1.1Suppose that(V1)–(V2)and(f1)–(f5)are satis fied.Then there exists λ∗>0 such that for each λ > λ∗,problem(1.1)has a ground state solution. Remark 1.1Shang and Zhang in[32]studied the existence of ground state solutions for critical problem Zhang et al.in[36]showed the existence of ground states for subcritical problem In both these papers,the authors assumed that fsatis fies monotone conditions.Moreover,as mentioned above,the operatorcan be reduced to the operator(−∆)sif the magnetic field A≡0.Hence our result is different from their and extends their results to some extent. Clearly,a weak solution of problem(1.1)is a critical point of the following functional Let us de fine and where Clearly,by(V2),(f4),(f5)–(i)and(iv)we have Iλ(u) ≤ Iλ,p(u)for all u ∈ E.Moreover,for ϕ∈E, To begin with,we give some lemmas. Lemma 2.1For λ>0 we have (i)for each u ∈ E{0},there exists a unique tu>0 such that α(tu)=α(t),α′(t)>0 for 0 (ii)for each v ∈ E{0},there exists a unique tv>0 such that β(tv)=β(t),β′(t)>0 for 0 (iii)there exists t0>0 such that tu≥t0for each u∈S1:={u∈E:kuk=1}and for each compact subset W⊂S1,there exists CW>0 such that tu≤CWfor all u∈W; (iv)there exists ρ >0 such that,where Proof(i)By(f1)–(f2),for any ε>0,there exists Cε>0 such that and for all(x,u)∈RN×R.Consequently,for ε>0 sufficiently small,(2.2)implies that for small t>0,and from(2.1)we can deduce that for small t>0.Moreover,by virtue of(f4)we have as t→ +∞.Hence α has a positive maximum and there exists tu>0 such that α′(tu)=0 and α′(t)>0 for 0 We claim that α′(t)6=0 for all t>tu.Indeed,if the conclusion is false,then,from the above arguments,there exists tu a contradiction. Combining the claim with prior arguments,we obtain the first conclusion of(i).The second conclusion is an immediate consequence of the fact that α′(t)=t−1h(tu),tui.This completes the proof of(i).Similarly,we can prove that(ii)holds. (iii)For u ∈ S1,by(i),there exists tu>0 such that tuu ∈ N.Hence for ε>0 small,(2.1)implies that As a consequence,there exists t0>0 such that tu≥t0for all u∈S1.We argue by contradiction to prove that tu≤CWfor all u∈W⊂S1.Suppose that there exists{un}⊂W⊂S1such that tn:=tun→+∞as n→∞.Since W is compact,there exists u∈W such that un→u in E.Consequently,by(f4)we deduce that as n→∞.But,(f3)implies that which gives a contradiction.So conclusion(iii)follows. (iv)For λ >0 and u ∈ Sρ,by the proof of(i)we know that for small ρ >0.Furthermore,for every u ∈ N,there exists t1>0 such that t1u ∈ Sρ.Hence by(i)we have Lemma 2.2Iλis coercive on N,i.e.,Iλ(u)→+∞ as u∈N and kuk→∞. ProofIf the conclusion is false,then there exist a sequence{un}⊂N and a positive number d such that→ ∞ and Iλ(un)≤ d.Set wn=.Then,up to a subsequence,we have Since wn6=0,there exists a point y∈RNsuch thatThen the integral absolute continuity implies that β (z)is continuous on RN. Hence By the continuity of β and the compactness of(0),there exists(0)such thatTherefore By the properties of the complex number we can easily obtain the pointwise diamagnetic inequality Hence we can proceed as in Lemma 3.1 in[16]to prove that if u∈E,then|u|∈Hs(RN,R)and the following fractional diamagnetic inequality holds.Consequently i.e.,{|wn|}is bounded in Hs(RN,R).So in view of Lemma 3.8 in[10]we know that|wn|→0 in(RN,R).By the interpolation inequality,one has as n→∞,a contradiction,which indicates that the assertion that is valid.Consequently,by(f4)we obtain for large n,a contradiction.This completes the proof. Lemma 2.3There exists λ∗>0 such that 0 ProofIf the conclusion is false,then there exists a sequence{λn}with λn→ +∞ such that cλn≥.Take u ∈ E{0}.Then by Lemma 2.1(i),there exists a unique tλn>0 such thatIλn(tu)=Iλn(tλnu).Hence by(f4)we have which implies that{tλn}is bounded in R.Hence,up to a subsequence,there exists t0≥ 0 such that tλn→ t0as n → ∞.If t0>0,then,in view of(f4)and Fatou’s lemma,we have But,on the other hand, a contradiction.Hence t0=0.Set w=tλnu.Then Consequently,again by(f4)one has as n→∞.Hence a contradiction.This completes the proof. De fine the mapping m:S1→N by setting m(w):=tww,where twis as in Lemma 2.1. Lemma 2.4(see[31])The mapping m is a homeomorphism between S1and N,and the inverse of m is given by Considering the functional ψλ:S1→ R given by then we have the following lemma. Lemma 2.5(see[31]) (i)If{wn}is a Palais-Smale sequence for ψλ,then{m(wn)}is a Palais-Smale sequence for Iλ.If{un} ⊂ N is a bounded Palais-Smale sequence for Iλ,then{m−1(un)}is a Palais-Smale sequence for ψλ. (ii)w ∈ S1is a critical point of ψλif and only if m(w)is a nontrivial critical point of Iλ. Moreover,the corresponding values of ψλand Iλcoincide and (iii)A minimizer of Iλon N is a ground state of eq.(1.1). Lemma 2.6If{un}⊂E satis fies un⇀0 in E and ϕn∈E is bounded in E.Then and and ProofFor any ε>0 and R>0,set where h appears in(f5)–(ii).By h ∈ H we can deduce that there exists R1>0 such that|Dε(R1)|< ε.By un⇀ 0 in E,we have for large n.Note that By Hölder inequality,(2.6)and the boundedness of{kunk}and{kϕnk}we can derive that and for large n and i.e.,(2.4)holds.Similarly,by(V2)we can conclude that(2.3)holds and for all t∈[0,1].Consequently, i.e.,(2.5)holds.This completes the proof. Proof of Theorem 1.1By Lemma 2.5(iii),it suffices to prove that the in fi mum cλis attained for fixed λ > λ∗.For fixed λ > λ∗,let{wn} ⊂ S1be a minimizing sequence satisfyingby Lemma 2.5(ii).By the Ekeland variational principle,we suppose ψ′λ(wn)→0 in E∗.Set un=m(wn)∈N.Then Lemma 2.5(i)implies that Iλ(un)=ψλ(wn)→cλand(un)→0 in E∗.By Lemma 2.2 we see that{un}is bounded in E.Therefore,up to a subsequence,there exists u∈E such that un⇀u in E,un→u in(RN,C)for 2≤t Since un⇀ u in E,by the de finition of weak convergence we know that hun,ϕi→ hu,ϕi.Furthermore,in the light of(2.1)and Young’s inequality we derive that Set Then 0 ≤ Gδ,n(x) ≤ Cδ|ϕ|2+2|u||ϕ|+C1Cδ|ϕ|q+C2|u|q−1|ϕ|∈ L1(RN)and Gδ,n(x)→ 0 a.e.on RN.By Lebesgue dominated convergence theorem,we haveRRNGδ,n(x)dx→0 as n→∞.Hence By the arbitrariness of δ,we know that Similarly,we can deduce that Thus(2.7)implies that Case 1u 6=0.Then u ∈ N and cλ≤ Iλ(u).Consequently,by weakly lower semicontinuity of the norm,Fatou lemma and(f3)one has which means that Iλ(u)=cλ. Case 2u=0.We shall apply the concentration-compactness principle due to Lions to the sequence of L1functions|un|2and we know that two cases may happen. Case(ii) Nonvanishing,i.e.,there exist a sequence{yn} ⊂ RNand a constant δ>0 such that If the former occurs,as mentioned above,by virtue of Lemma 3.8 in[10]we have|un|→0 in Lt(RN,R)for 2 As a consequence and Then cλ≥,which contradicts with Lemma 2.3.As a consequence,the latter occurs. Without loss of the generality,we may assume that yn∈ZN.Set(·)=un(·+yn).Up to a subsequence,there existsu¯∈E such that⇀in E,in(RN,C)for 2≤ t Step 1We prove that=0.Indeed,for all ϕ∈E,set ϕn(·):=ϕ(·−yn).In view of Lemma 2.6 we conclude thatZ and Consequently, Step 2We claim that≤cλ.Indeed,by the boundedness of{}and Lemma 2.6 we have and and Consequently, Again by the periodicity of Vpand fpin the variable x,weakly lower semi-continuity of the norm,(f5)–(iii)and Fatou lemma we deduce that Step 3We prove thatIndeed,by6=0 and=0 we have ¯u∈Np.Consequently,Lemma 2.1(ii)implies that the conclusion holds. All in all,cλis attained.And then the corresponding minimizer is a ground state of eq.(1.1)by Lemma 2.5(iii).This completes the proof.

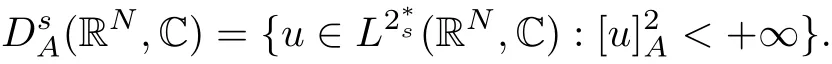
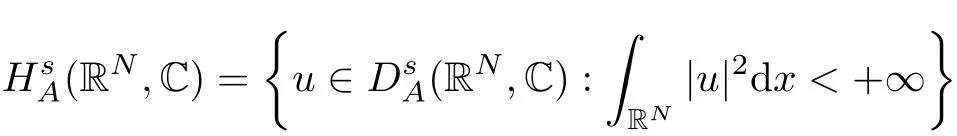
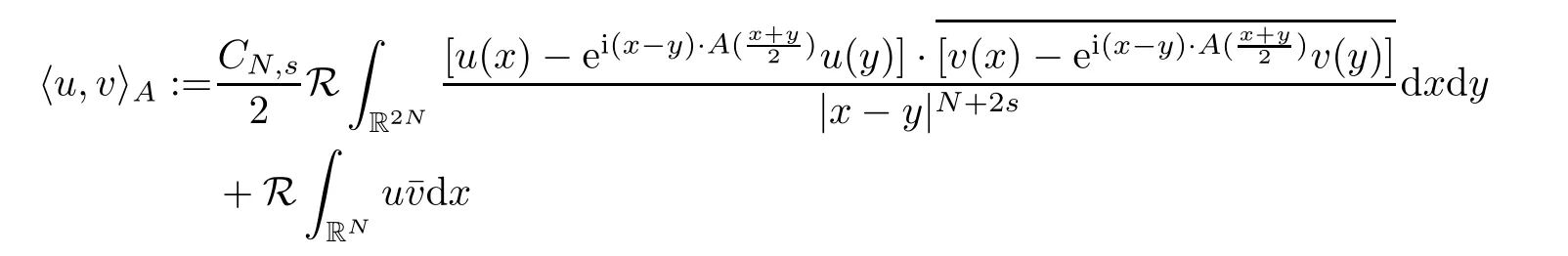

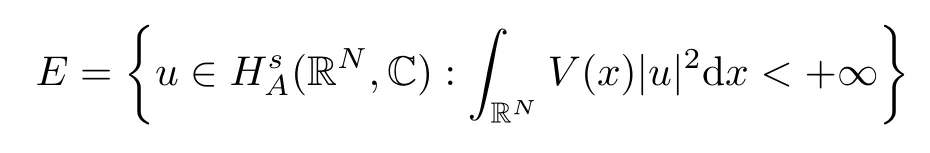
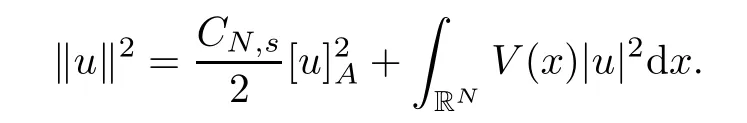

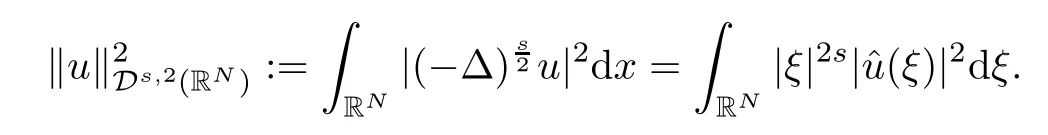

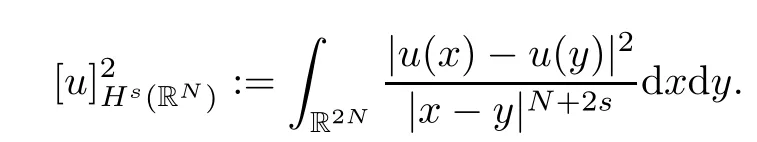


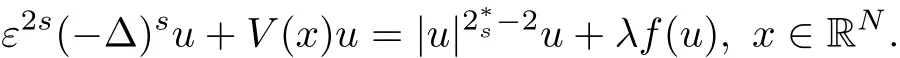



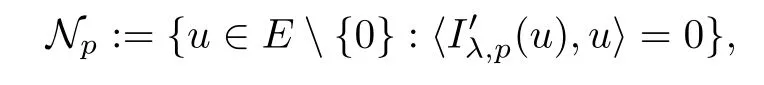
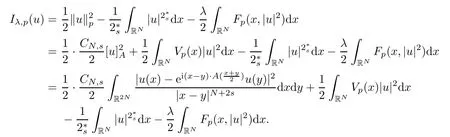
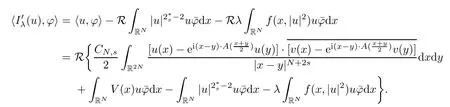
2 Proof of Theorem 1.1


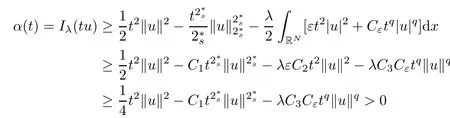
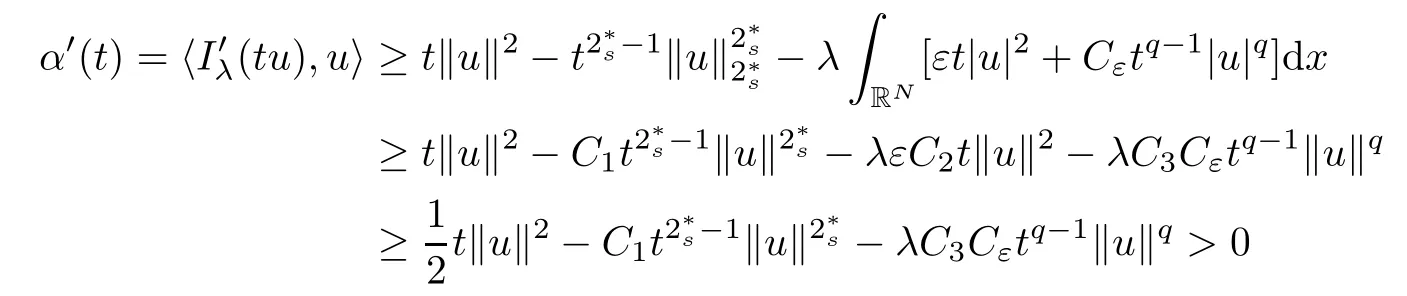

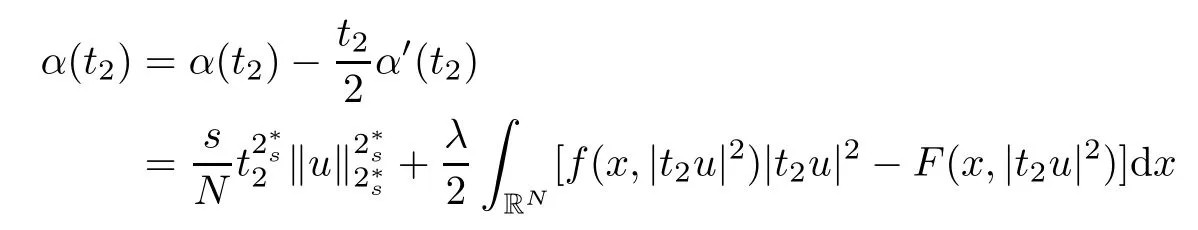

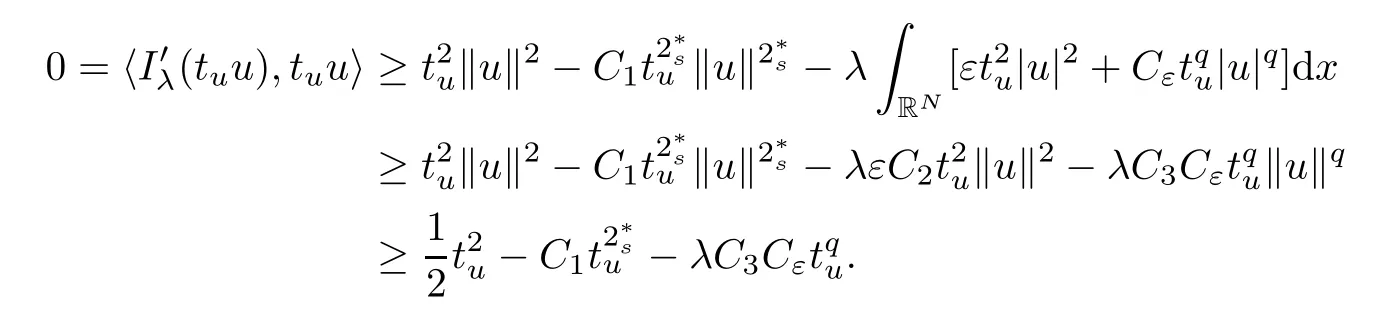
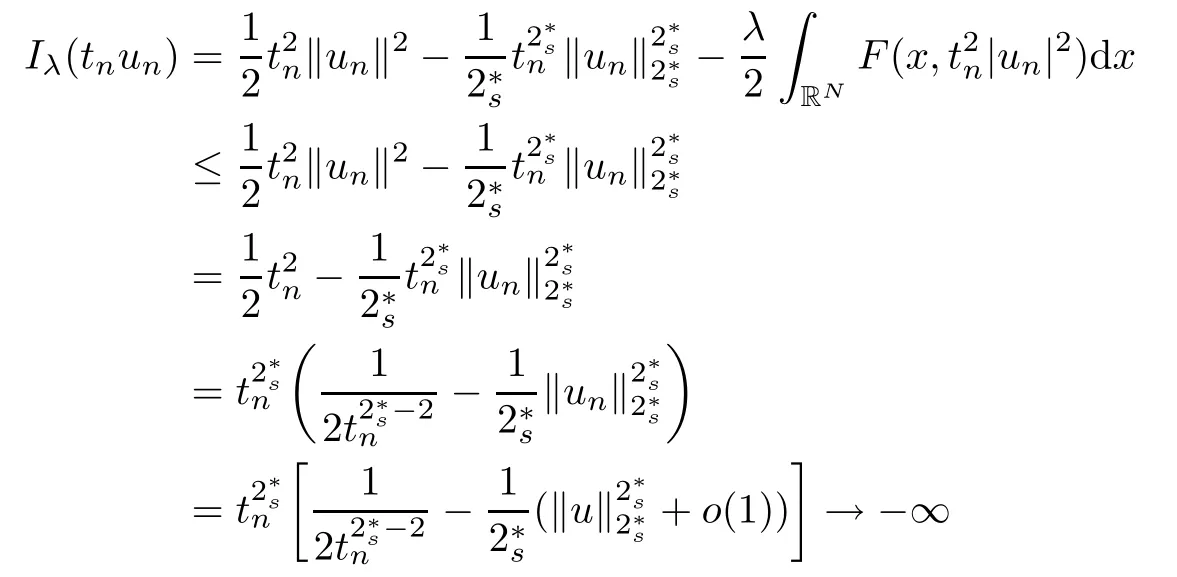



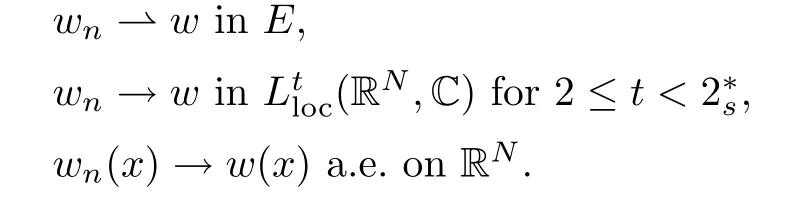
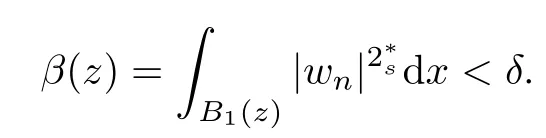




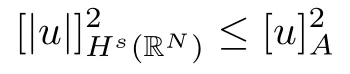
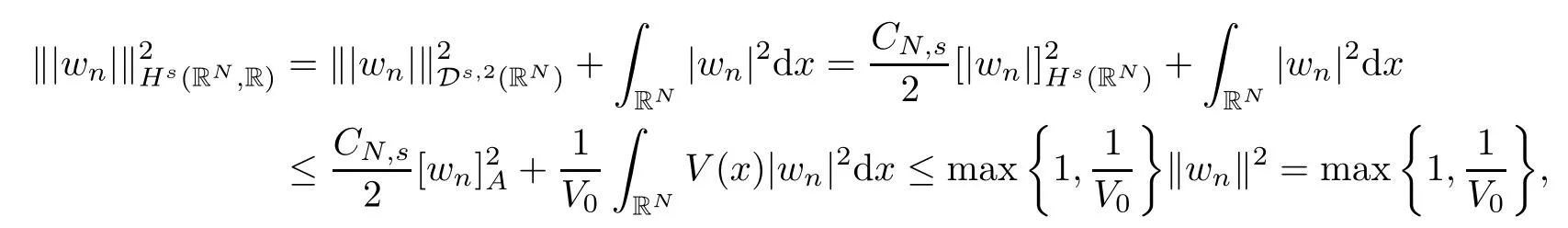

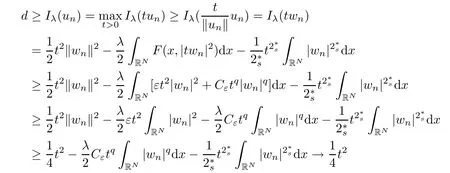
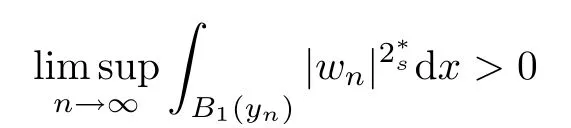

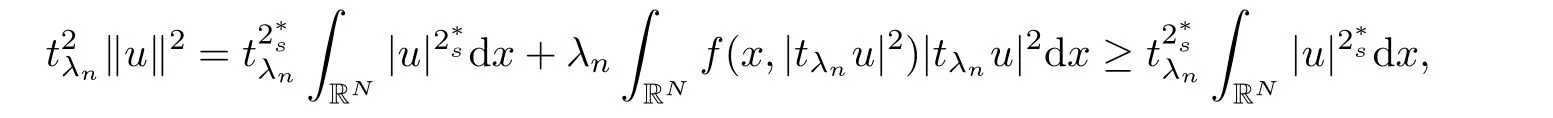







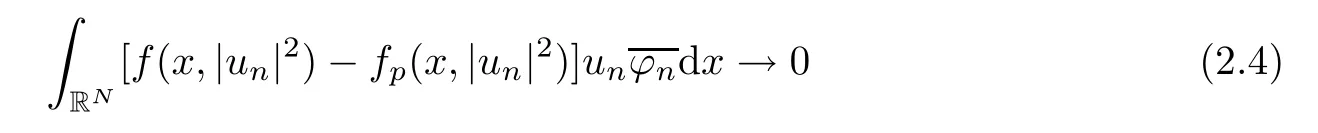
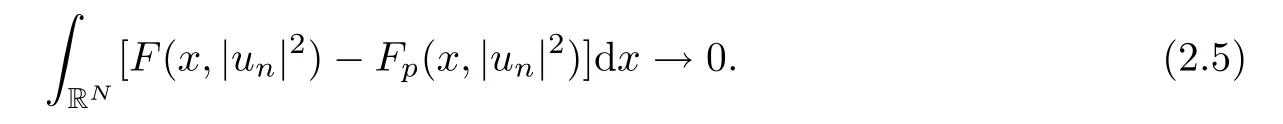

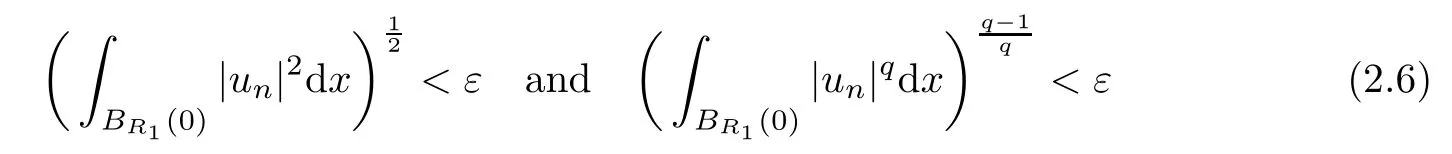
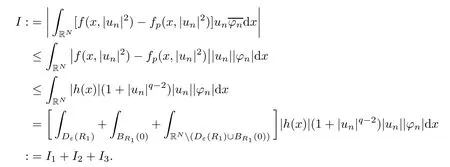

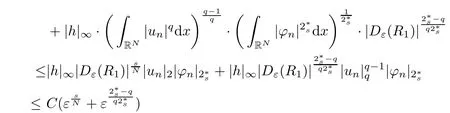
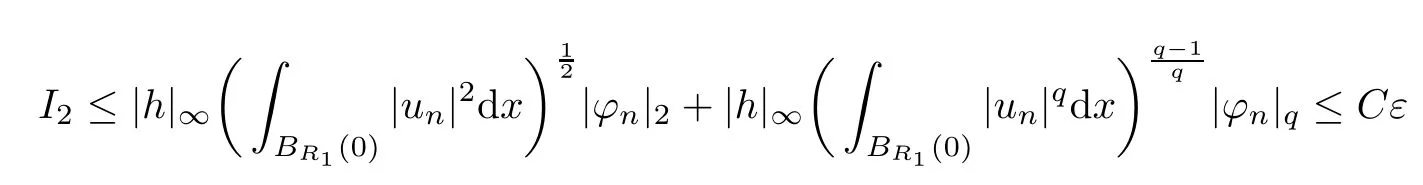
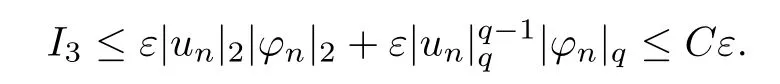
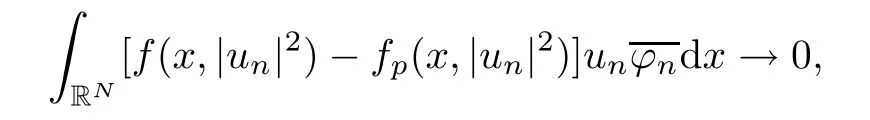
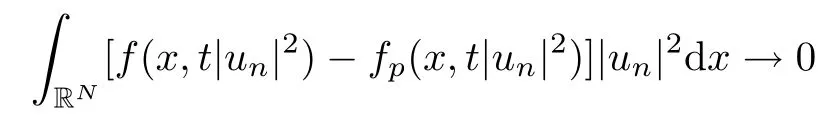
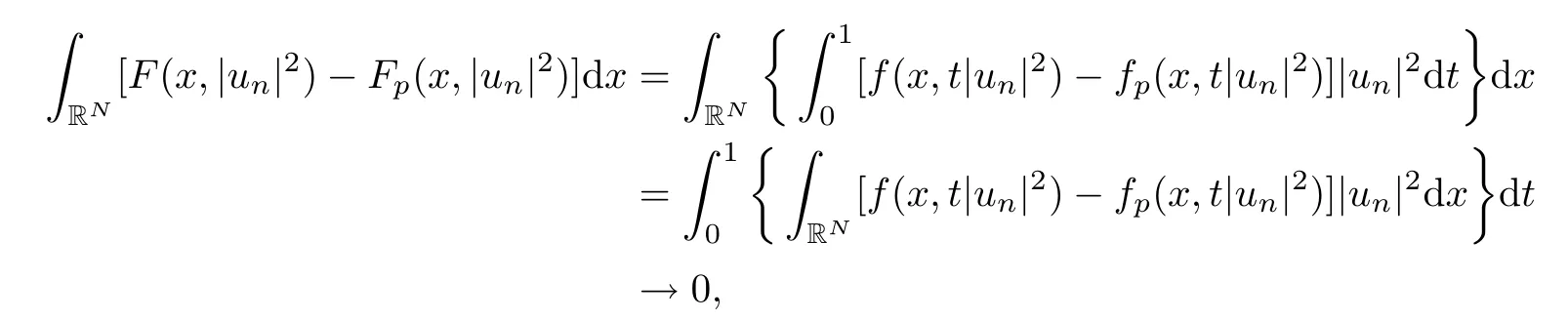


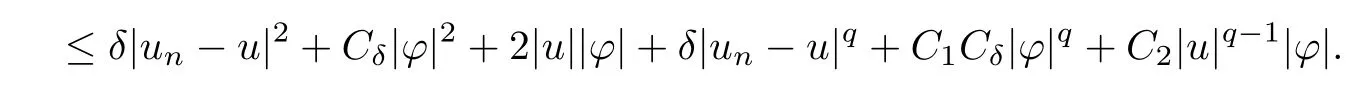


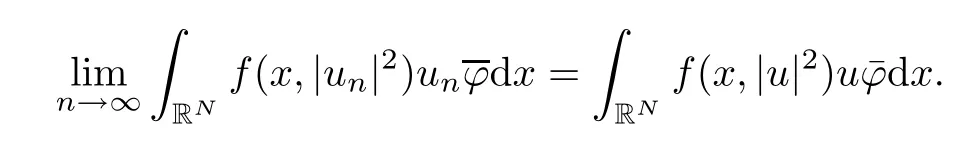
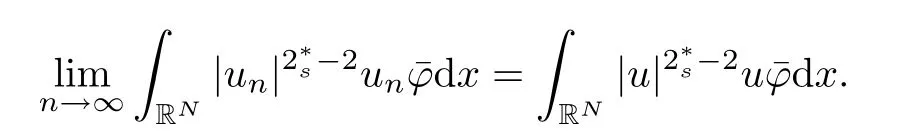
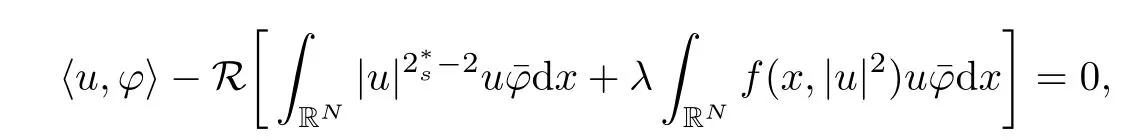
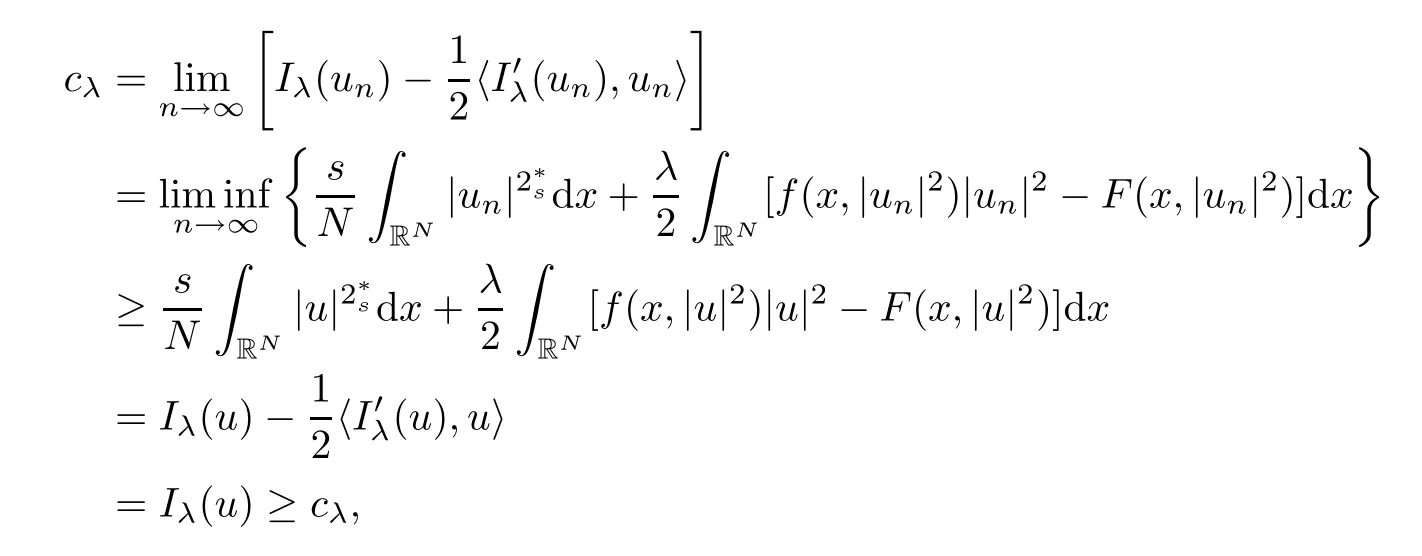
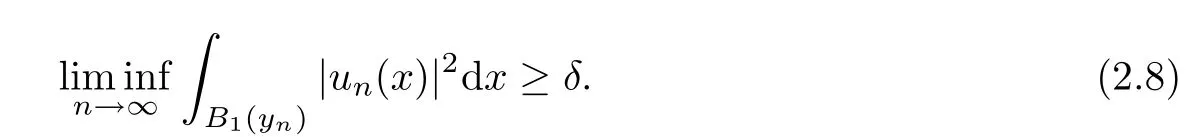
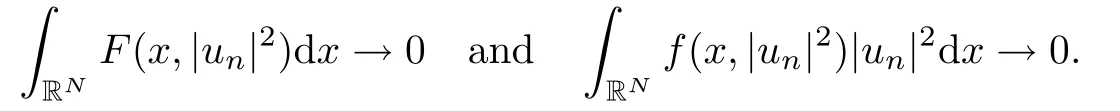
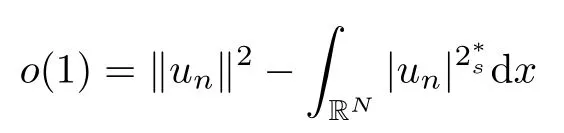





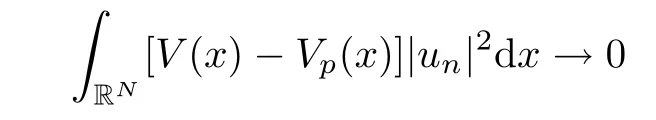
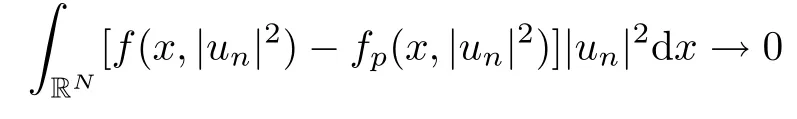
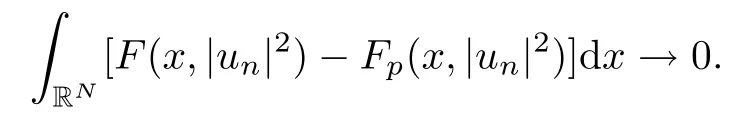
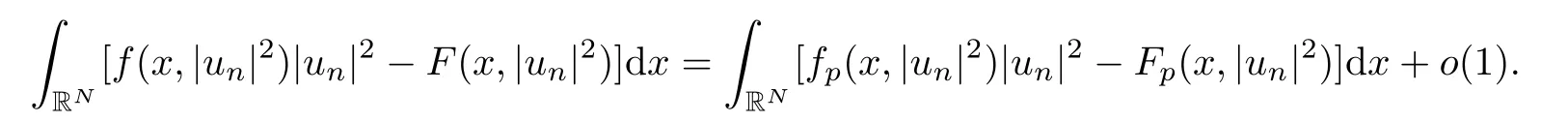
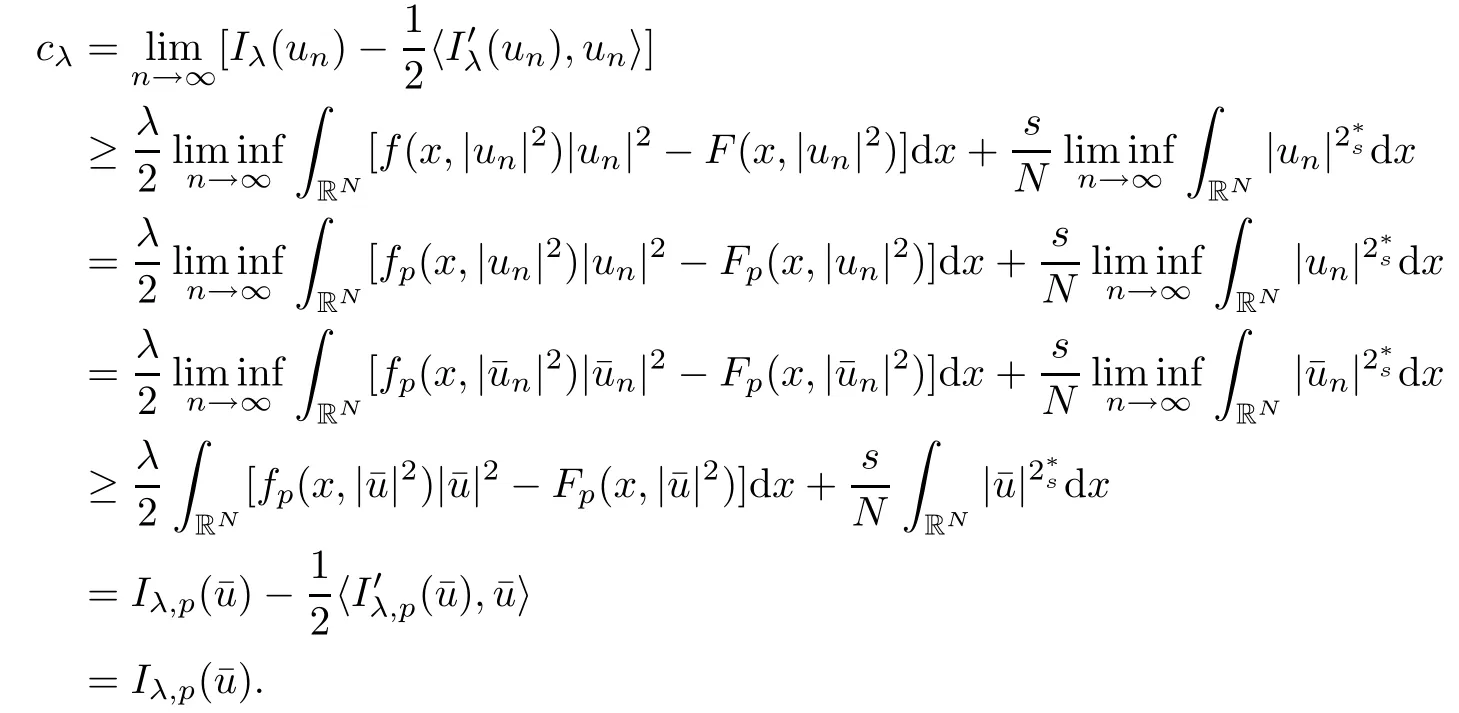
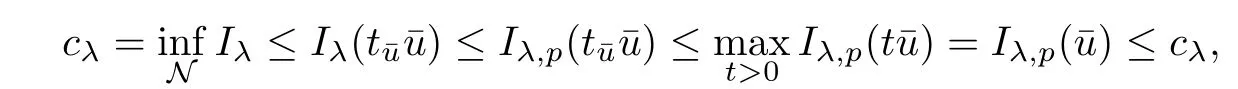
 Acta Mathematica Scientia(English Series)2020年1期
Acta Mathematica Scientia(English Series)2020年1期
