THE EXISTENCE AND LOCAL UNIQUENESS OF MULTI-PEAK POSITIVE SOLUTIONS TO A CLASS OF KIRCHHOFF EQUATION∗
Gongbao LI(李工宝) Yahui NIU(牛亚慧)
Hubei Key Laboratory of Mathematical Sciences and School of Mathematics and Statistics,Central China Normal University,Wuhan 430079,China
E-mail:ligb@mail.ccnu.edu.cn;yahuniu@163.com
Abstract In the present paper,we consider the nonlocal Kirchho ffproblemwhere a,b>0,1
Key words Kirchho ffequations;multi-peak positive solutions;local uniqueness;local Pohozaev identity;Lyapunov-Schmidt reduction
1 Introduction and Main Results
In this paper,we consider the existence and local uniqueness of muti-peak positive solutions to the following singularly perturbed Kirchho ffproblem

where a,b>0,1
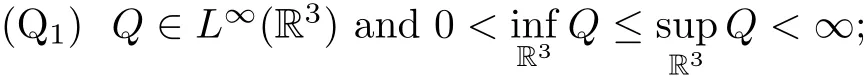
(Q2)there exist θ∈ (0,1)and k(k ≥ 2)distinct points{b1,···,bk} ⊂ R3such that for everyand

(Q3)There exist m>1,η>0,k∈N,bj=(bj,1,bj,2,bj,3)∈R3,cj,i∈R with cj,i6=0 for each i=1,2,3 and j=1,···,k such that

where x=(x1,x2,x3)∈R3.
To be precise,we first give the de finition of k-peak solutions of eq.(1.1)as usual.
De finition 1.1Let k∈N,bj∈R3,1≤j≤k.We say that uǫ∈H1(R3)is a k-peak solution of(1.1)concentrated at{b1,···,bk},if
(i)uǫhas k local maximum points xjǫ∈ R3,j=1,2,···,k,satisfying

as ǫ→ 0 for each j;
(ii)for any given τ>0,there exists R ≫ 1,such that

(iii)there exists C>0 such that

Problem(1.1)and its variants were studied extensively in the literature.To extend the classical D’Alembert’s wave equations for free vibration of elastic strings,Kirchho ff[20]proposed for the first time the following time dependent wave equation

Bernstein[4]and Pohozaev[25]studied the above type of Kirchho ffequations quite early.Since Lions[22]introduced an abstract functional framework to this problem,much attention was received,such as[1,11]and the references therein.
Problem(1.1)is a typical case of the equation

where V:R3→R is a bounded continuous function.First,we review some known results on(1.2)in the case where f(x,u)=f(u).He and Zou[18]considered problem(1.2)where V is assumed to satisfy the global condition of Rabinowitz[26]
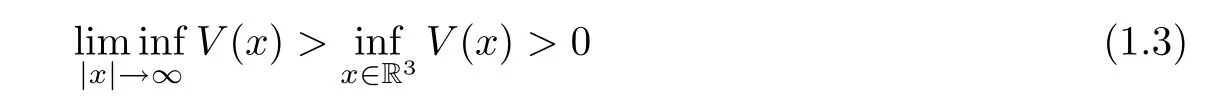
and f:R→R is a nonlinear function with subcritical growth of type uqfor some 3 They proved the existence of multiple positive solutions to(1.2)for ǫ sufficiently small.Later,Wang et al.[27]extended the result of[18]to the case of critical growth,they established some existence and nonexistence results for(1.2)where f(u)∼ λg(u)+u5,V and g satisfy similar conditions as that of[18].By a penalization method,He,Li and Peng[17]improved an existence result of Wang et al.[27]by allowing that V only satis fies a local condition:there exists a bounded open set Ω⊂R3such that Afterwards,by introducing a new manifold and applying a new approximation method of[13],He and Li[16]proved the existence of solutions for ǫ sufficiently small to problem(1.2)where f(u)∼uq+u5,1 On the other hand,if a=1,b=0,R3is replaced by RN,(1.1)reduces to the problem where 1 admits a unique positive solution(up to translations)which is also nondegenerate(see e.g.[3,10]).Basing on this uniqueness and nondegeneracy property,by using the Lyapunov-Schmidt reduction method,Cao et al.[7]and Cao et al.[6,8],Noussair and Yan[24]proved the existence of solutions to eq.(1.5)for ǫ>0 sufficiently small on bounded domains and in the whole space,respectively.As far as we know,the results on the uniqueness of solutions which have the concentration phenomena are few,we only mention the recently work by Cao[5],which proved the local uniqueness of multi-peak positive solutions to equation −ǫ2∆u+V(x)u=up.For more work concerning the uniqueness of solutions with the concentration phenomena,one can also refer to[7,14]. We remark that all the results of Kirchho ffequation mentioned above were derived by variational methods.To deal with nonlinearity of type uqfor q in different subintervals of(1,5],different variational methods have to be applied.Recently,Li et al.[21]and Luo et al.[23]dealt with(1.2)(where f(x,u)=up)in the case of 1 Motivated by the work of[21]and[24],we study the existence and local uniqueness of multipeak positive solutions to the problem(1.1)by Lyapunov-Schmidt reduction method.Here,by local uniqueness,it means that ifare two solutions of equation(1.1)concentrating at the same family of concentration points,thenfor ǫ sufficiently small. Before stating our main results,we introduce the following notation.Denote The energy functional corresponding to eq.(1.1)is for u∈Hǫ,where u+=max(u,0). We call u ∈ Hǫa(weak)solution to eq.(1.1)if for any ψ ∈ Hǫ,it holds that Similar to the proof in[23,Proposition 2.3],we can prove that the limiting problem of eq.(1.1)is given by the following system the positive solution of(1.8)(we denote it by(U1,···,Uk))is unique and each Uiis also nondegenerate in H1(R3)in the sense that for ϕ∈H1(R3). Our main result is as follows. Theorem 1.2Assume that Q(x)satis fies(Q1)and(Q2).Then,for ǫ>0 sufficiently small,equation(1.1)has a k-peak solution de fined as in De finition 1.1 concentrating around bi,1≤i≤k. Theorem 1.3Assume that Q(x)satis fies(Q1)and(Q3).If,j=1,2,are two k-peak solutions,then for ǫ sufficiently small,we have for i=1,···,k. Remark 1.4If we replace condition(Q2)in Theorem 1.2 by Remark 1.5Our main result Theorem 1.2 extend the main results in[24]which considered the Schrödinger equation(1.5)to the Kirchho ffequation(1.1). We will follow the scheme of Cao and Peng[9]to prove Theorem 1.2 by using the Lyapunov-Schmidt reduction.The main difficulties are the appearence of the nonlocal term?R?∆u,which brings more technical difficulties than Schrödinger equation(1.5)did.Moreover,when we prove the existence and local uniqueness of the multi-peak solution of(1.1),on the one hand,there are many cross iterms,and on the other hand,the limiting equation of(1.1)is in fact a system of partial differential equations(1.8),which is different from the case of singlepeak solution and Schrödinger equation(1.5),the difference of these two aspects also make the estimate more complex. Now,we give the main idea of the proof of Theorem 1.2.Our arguments are based on the variational method.The basic idea is to use the unique positive solution of the system(1.8)as the building block to construct solutions for(1.1).Following the scheme of Luo et al.[23],we will construct solutions of the formThen we reduce the problem we are dealing with to a finite-dimensional one by a type of Lyapunov-Schmidt reduction.The nonlocal term?RR3|∇u|2?∆u brings more delicate and complicate estimates on the orders of ǫ. Next,we give the main idea of the proof of Theorem 1.3.We will follow the idea of Cao,Li and Luo[5].More precisely,if,i=1,2,are two distinct solutions,derived as in Theorem 1.2,then it is clear that the function Our notations are standard.We writeRu to denote Lebesgue integrals over R3,unless otherwise stated,and.We use BR(x)(andto denote open(and close)balls in R3centered at x with radius R. By the usual abuse of notations,we write u(x)=u(r)with r=|x|whenever u is a radial function in R3.We will use C and Cj(j∈N)to denote various positive constants,and O(t),o(t)to mean|O(t)|≤C|t|and o(t)/t→0 as t→0,respectively. The paper is organized as follows.In Section 2,we give some notations and some preliminary estimates which play a key role in the rest of the arguments.In Section 3,we prove Theorem 1.2 and in Section 4 we prove the local uniqueness results. Let Iǫbe given by(1.7),we can easily check that Iǫ∈ C1(Hǫ),so its positive critical points are solutions of eq.(1.1).We will restrict ourselves to the existence of critical points of Iǫof the the following form where To construct solutions to eq.(1.1)in form(2.1),we will follow the scheme of Cao and Peng[9],combining reduction method and variational method.We denote and let Let 0<δ Note that since the unique positive solution of equation−∆u+u=Q(bi)updecays exponentially at in fi nity,we infer that for some σ>0. Note that if(x1,···,xk)∈ Dδ,then|xi−xj|≥ |bi− bj|/2 ≥ 2δ with i 6=j,which implies by(2.3)that for any given r,s>0,where γ>0 is constant. De fine for X=(x1,···,xk)∈ R3kand ϕ ∈ Hǫ. Expand Jǫ(X,ϕ)near ϕ =0 for each fixed X: where Jǫ(X,0)=Iǫ(Hǫ,X),and operators hǫ,Lǫand Rǫas follows:for ϕ,ψ ∈ Hǫ, and For every ǫ,δ>0 sufficiently small and for every fixed X ∈ Dδ,we will prove that Jǫ(X,·):Eǫ,X→ Eǫ,Xhas a unique critical point ϕǫ,X∈ Eǫ,X,Then,for each ǫ,δ sufficiently small,we will find a critical point Xǫfor the function Fǫ:Dδ→R induced by It is standard to verify that(Xǫ,ϕǫ,Xǫ)is a critical point of Jǫfor ǫ sufficiently small by the chain rule.Furthermore,by Bartsch and Peng[2],we have the following lemma. Lemma 2.1There exist ǫ0>0, δ0>0 satisfying the following property:for any ǫ∈(0,ǫ0)and δ∈ (0,δ0),Xǫ∈ Dδis a critical point of the function Fǫde fined as in(2.8)if and only if is a critical point of Iǫ. As a result,we obtain a solution uǫ≡ Hǫ,Xǫ+ϕǫ,Xǫto eq.(1.1). In the rest of this section,we will estimate lǫ:Hǫ→ R and Rǫ:Hǫ→ R,which will combine with the invertibility of operator Lǫbe used to prove the existence of unique critical point ϕǫ,Xof Jǫ(X,ϕ)for every fixed X ∈ Dδ. Lemma 2.2Assume that Q satis fies(Q1)and(Q2).Then,there exists a constant C>0,independent of ǫ,δ,such that for any X ∈ Dδthere holds for ϕ ∈ Hǫ,here θ denotes the order of Hölder continuity of Q in the neighborhood of bj,1≤j≤k. ProofFirst,we have To estimate h1,using(2.4)yields To estimate h2,note that So Finally,combining the above estimates gives the required estimate. Lemma 2.3There exists a constant C>0,independent of ǫ and b such that for i ∈{0,1,2},there hold for all ϕ∈Hǫ,where R(i)ǫis the ith derivative of Rǫ. ProofThis lemma can be proved by the similar method as that of Lemma 3.3 in[21]. Next we consider the operator Lǫde fined as in(2.6). Proposition 2.4For ǫ small enough and X ∈ Dδ,the operator Lǫis invertible on Eǫ,Xwith uniformly bounded inverse.In other words,there exists ǫ1,δ1and ρ >0 such that for all ǫ∈ (0,ǫ1),δ∈ (0,δ1)and all X ∈ Dδ,there holds As the proof of Proposition 2.4 is standard,we leave it in Appendix. In the last of this section,we give the estimate of Iǫ(Hǫ,X). Lemma 2.5Assume that Q(x)satis fies(Q1)and(Q2).Then for ǫ>0 sufficiently small,we have where and and θ is the Hölder continuity of Q(x)in the neighborhood of bj,1 ≤ j ≤ k. ProofRecall that Since estimates(2.4)hold for i 6=j,hence,for ǫ>0 sufficiently small,we have for some γ>0. As Uisatis fies eq.(1.8),thussatis fies Combining with the following elementary inequalities we have The required estimate follows from(2.11)and(2.12). In this section,we prove Theorem 1.2.First,we give the result of the existence of the reduction map ϕǫ,X. Proposition 3.1For ǫ, δ sufficiently small,there exists a C1map ϕǫ,X:Dδ→ Hǫwith∈ Eǫ,Xsatisfying Moreover,we can choose τ∈ (0,θ/2)as small as we wish such that This proposition can be proved by the similar arguments as that of Li et al.[21]by using Lemma 2.2,Lemma 2.3 and Proposition 2.4.We omit the details. Now we prove Theorem 1.2. ProofFor given X ∈Dδ,by Proposition 3.1,we will find a critical point for the function Fǫde fined as in(2.8)by Lemma 2.1.We consider the minimizing problem Suppose Xǫ∈ Dδsatis fieswe claim that Xǫis an interior point of Dδand thus Xǫis a critical point of Fǫ,then by Lemma 2.1,uǫ≡ Hǫ,Xǫ+ϕǫ,Xǫis a solution of eq.(1.1),hence Theorem 1.2 follows. We prove the claim by a comparison argument.First,we analyze the asymptotic behavior of Fǫwith respect to ǫ.By the Taylor expansion,we have By using the method of the proof of Lemma 4.3 in[21],we getby direct computation.Combining(2.9),(2.10),(3.1)and Lemma 2.3,we have Let ej∈R3(j=1,···,k)with|ej|=1,ei6=ejfor i 6=j and=bj+ǫηejwith η>1 sufficiently large such that Zǫ=(,···,)∈Dδ.By the above asymptotical formula,we have Applying the Hölder continuity of Q,noting the fact that τ≪ θ/2,we derive that Thus,by using F(Xǫ)≤ F(Zǫ),we deduce If Xǫ∈∂Dδ,then by assumption(Q2),we have for some constants 0 This proves the claim.Hence,we finish tne proof. Remark 3.2If Q satis fies(Q1)and(),Theorem 1.2 can be proved by the similar arguments by replacing(3.2)with In this section,we prove the local uniqueness results Theorem 1.3.First,we give some important estimates:we will show that the estimates ofandin(2.2)can be improved step by step by using a Pohozaev type identity and assuming that Q(x)satis fies(Q3). The crucial Pohozaev type identity we will use is as follows. Proposition 4.1Let u be a positive solution of eq.(1.1).Let Ω be a bounded smooth domain in R3.Then,for each α=1,2,3,there hold here ν =(ν1,ν2,ν3)is the unit outward normal of∂Ω. Proposition 4.1 can be proved by multiplying both sides of equation(1.1)by ∂xαu for each 1≤α≤3 and then integrating by parts.We omit the proof,see Cao,Li and Luo[5,Proposition 2.3]for the detials. We recall an inequality:for any 2≤q≤6,there exists a constant C>0 depending only on n,a and q but independent of ǫ such that holds for all ϕ ∈ Hǫ.For a proof,see e.g.(3.6)of Li et al.[21]. Proposition 4.2Assume that be a solution derived as in Theorem 1.2.Then and ProofFor simplicity,we denote ϕ = ϕǫ,Xin the rest of this section.First,we prove(4.3)for fi x i ∈ {1,···,k}.Applying the Pohozaev-type identity(4.1)to u=uǫwith Ω =Bd(xiǫ),where 0 for any ϕ ∈ Hǫ.We have We estimate each side of(4.6)as follows.Using(2.2),a straightforward computation givesSo From(4.5)and(2.3),we know for any γ>0.Using similar arguments and choosing a suitable d if necessary,we also derive Furthermore,since Q(x)is bounded,from(4.2)and(4.5),we have Combing the above estimate and(4.6),we obtain for any γ>0. Next we estimate the left side of(4.8).Substituting the form of uǫinto the integral,and recall(2.4)and(4.2),we obtain for any given constant γ>0.By assumption(Q3),we have Thus,by(4.8),(4.9)and(4.10),we get The following inequality is elementary where a,b∈R,m>1,m∗=min{m,2},the constant C is independent of a,b. Applying(4.12)to a= ǫxα,b=− bi,α,we have Take α = α0such thatNote also that Thus,by(4.11),(4.13)and Hölder’s inequality,we have which implies Then,from(4.11),we obtain where tαis the αth component of t for α =1,2,3.As Ui(x)is radially symmetric decreasing,we get t=0.This yields(4.3). Next,we will use property Recall that summing over i in both sides of system(1.8)for Ui,we have as uǫis a solution of equation(1.1),we get As a result,ϕ must satisfy with Hence Furthermore,by the fact that we have and where γ>0 is a constant.By the similar estimate as the proof of Proposition 5.2 in[5],we have Z Combining the above estimate with(4.16)and(4.3),we obtain As a result, Thus we complete the proof of Proposition 4.2. In the rest of this section,we devoted to prove Theorem 1.3.We argue by way of contradiction.Assumeare two distinct solutions concentrating around bj(1≤j≤k)derived as in Theorem 1.2.Set then and where It is clear that We will prove that to obtain a contradiction. For fixed j ∈ 1,···,k,set To prove(4.21),we will prove thatandholds seperately.To this end,we will establish a series of results.First,we have Proposition 4.3There holds ProofAdding(4.19)and(4.20)together gives Multiply ξǫon both sides of(4.22)and integrate over R3.As the terms containing b is positive,we can throw away them,so Since Q is bounded,we have and where we have used(4.2).Hence which implies the desired estimate.The proof is complete. Next we study the asymptotic behavior of ξǫ,j. Proposition 4.4There exist dβ∈ R,β =1,2,3 such that(up to a subsequence) as ǫ→ 0. ProofWe will prove that the limiting function of ξǫ,jbelongs to the kernel of a linear operator associated to Uj.It is straightforward to deduce from(4.19)that ξǫ,jsolves We claim that ξj∈ KerLj,that is, Then by the fact that Ujis nondegenerate,we havefor some dβ∈ R(β =1,2,3),and thus Proposition 4.4 is proved. To deduce(4.24),we only need to show that(4.24)is the limiting equation of eq.(4.23).Observing that where we have used(2.3),(2.4)and(4.4),so as ǫ→ 0.For convenience,we denote for i=1,2.Similarly,we have Here,we have used(4.3),which implies Combining with implies for j 6=l as ǫ→ 0.From the above two formulas and ξǫ,j→ ξjin,we conclude that in H−1(R3).Also,as we have Finally,from(4.25)(4.26)(4.27),we obtain(4.24).The proof is completed. Proposition 4.5Let dβbe de fined as in Proposition 4.4.Then ProofApplying(4.1)toandwith Ω=,where d is chosen in the same way as that of(4.5),which combine with(4.4)and Proposition 4.3 implies Z and We obtain where 1≤α≤3 and By(4.7)and(4.4),we have by choosing γ>3+2m. By(4.28),(4.29)and Hölder’s inequality,we get As to Aǫ,by(2.3),we have for any given γ>0.Hence we can deduce that Hence by the above estimate,there holds On the other hand,as combining with assumption(Q3),we get as ci,α6=0.Combining with(4.3)and Proposition 4.4,we obtain Then dα=0 for α =1,2,3,since Uiis a radially symmetric decreasing function. Proof of Theorem 1.3By Propositions 4.4 and 4.5,we havefor any j=1,···,k.On the other hand,by using maximum principle,we can prove we can refer to[5,Proposition 3.5]for the similar detail proof.Consequently,we got(4.21),which contradict to=1.The proof of uniqueness is completed. Appendix In this section,we give the proof of Proposition 2.4. ProofWe use a contradiction argument.Assume,on the contrary,that there exist ǫn→0,δn→ 0 and Xn=(,···,)∈ Dδnand ϕn∈ En≡ Eǫn,Xnsuch that Since the equality is homogeneous,we may assume,with no loss of generality,that=. To deduce contradiction,for each i0=1,···,k,we introduce and Note also that and let hn∈.Substituting hninto(A2)and send n→∞,we get,by the same argument as that of[9,Appendix],that Claim that ϕ≡0.Indeed,since for each j=1,2,3,sending n→∞yields Recalling that Ui0decays exponentially,we have where ot(1)→∞ as t→∞.So We reach a contradiction.The proof is completed.


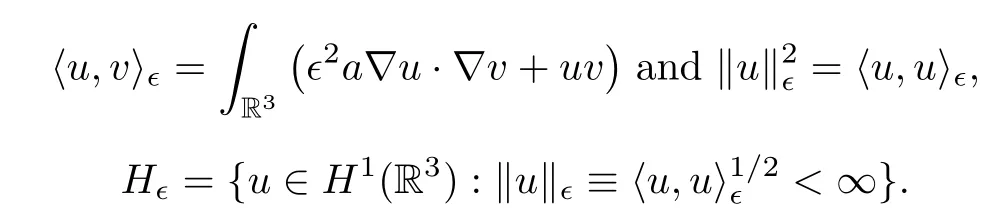

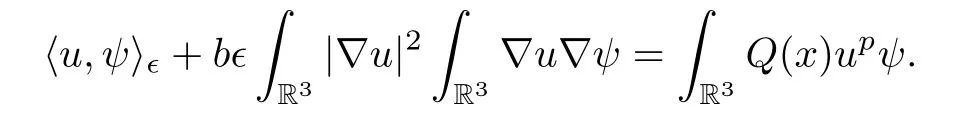





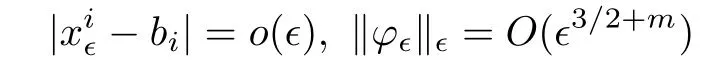
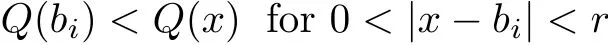

2 Preliminaries
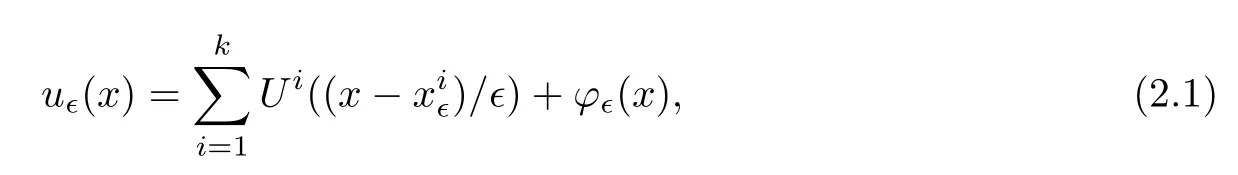
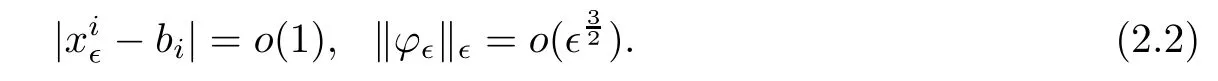





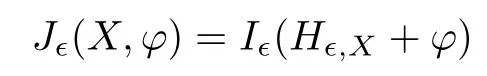



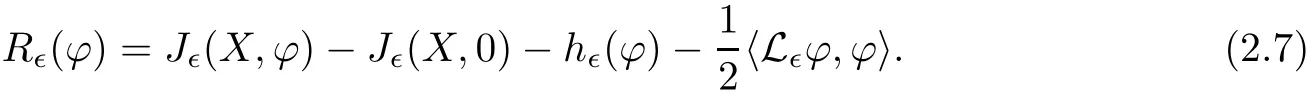











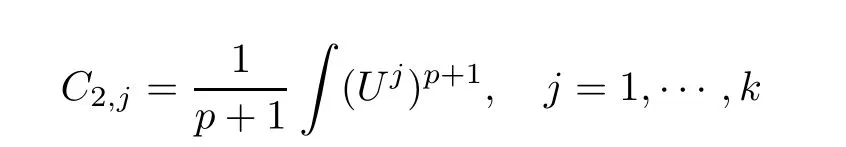



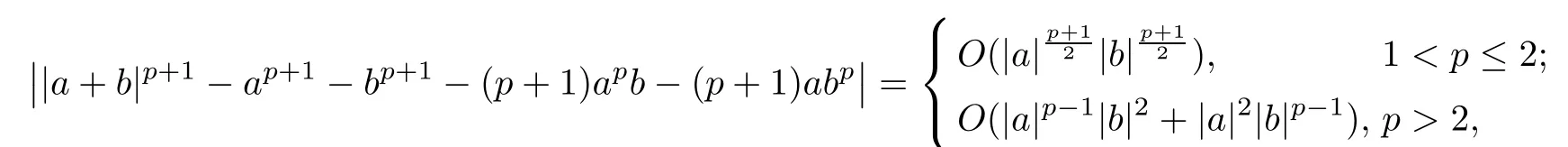

3 Proof of Theorem 1.2

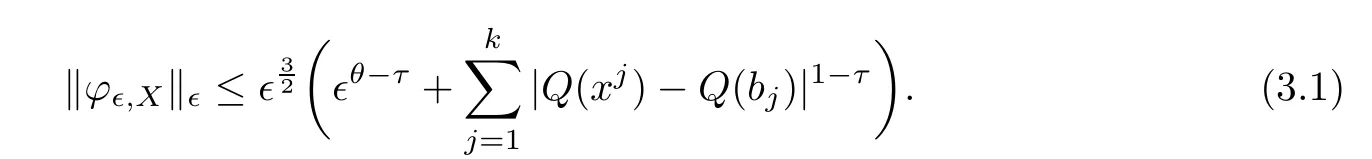


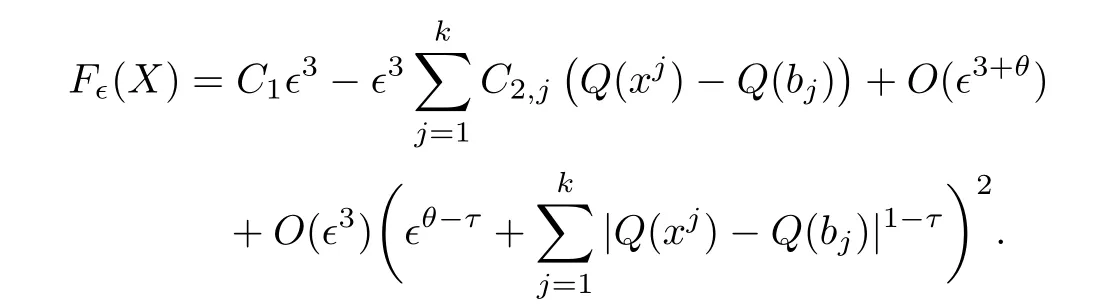
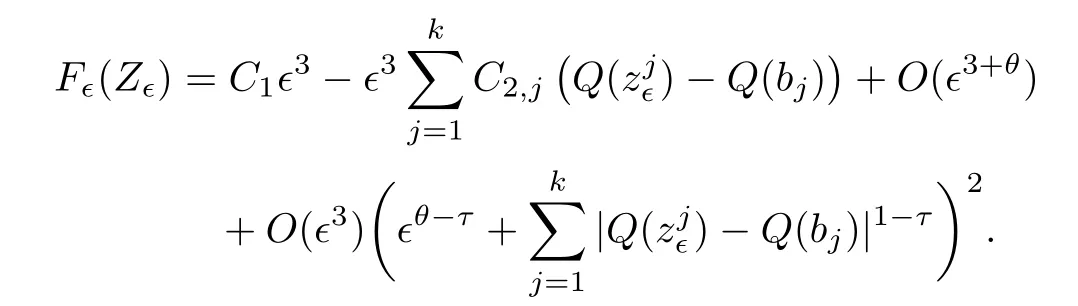
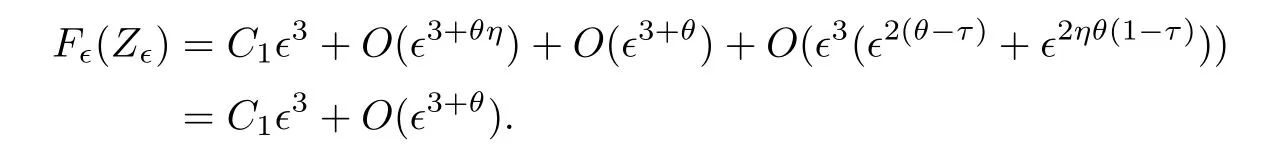

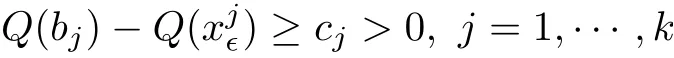
4 Local Uniqueness Results







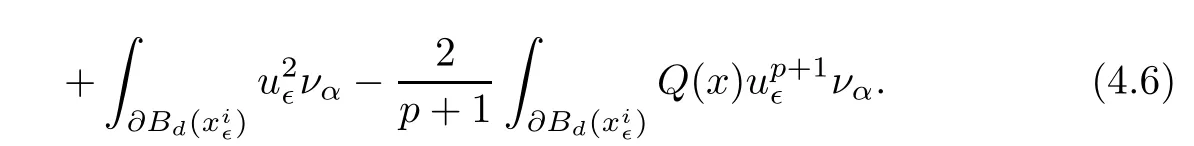


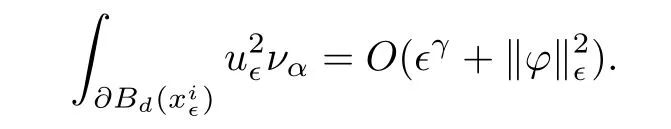
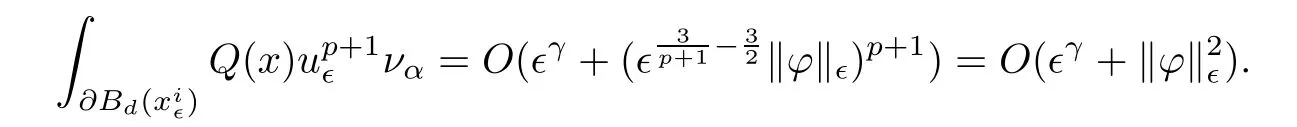


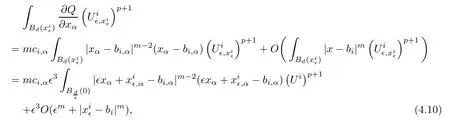
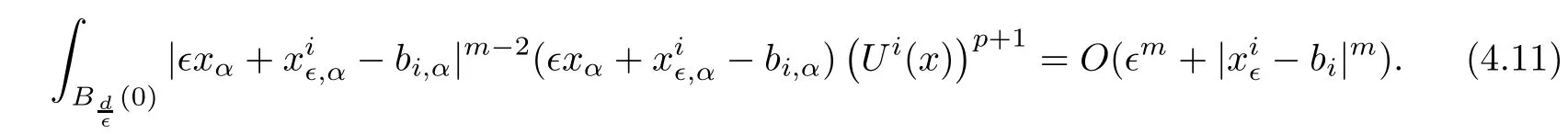
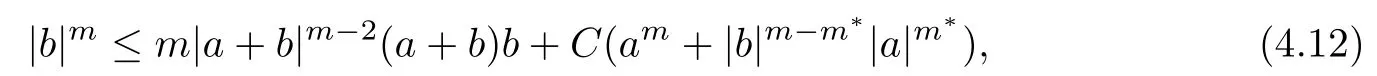

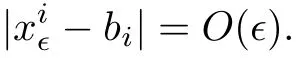


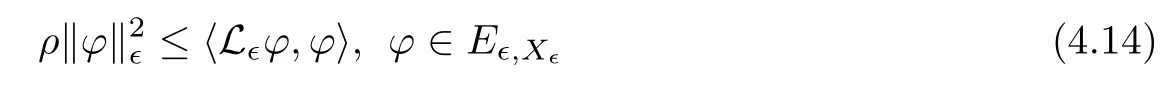




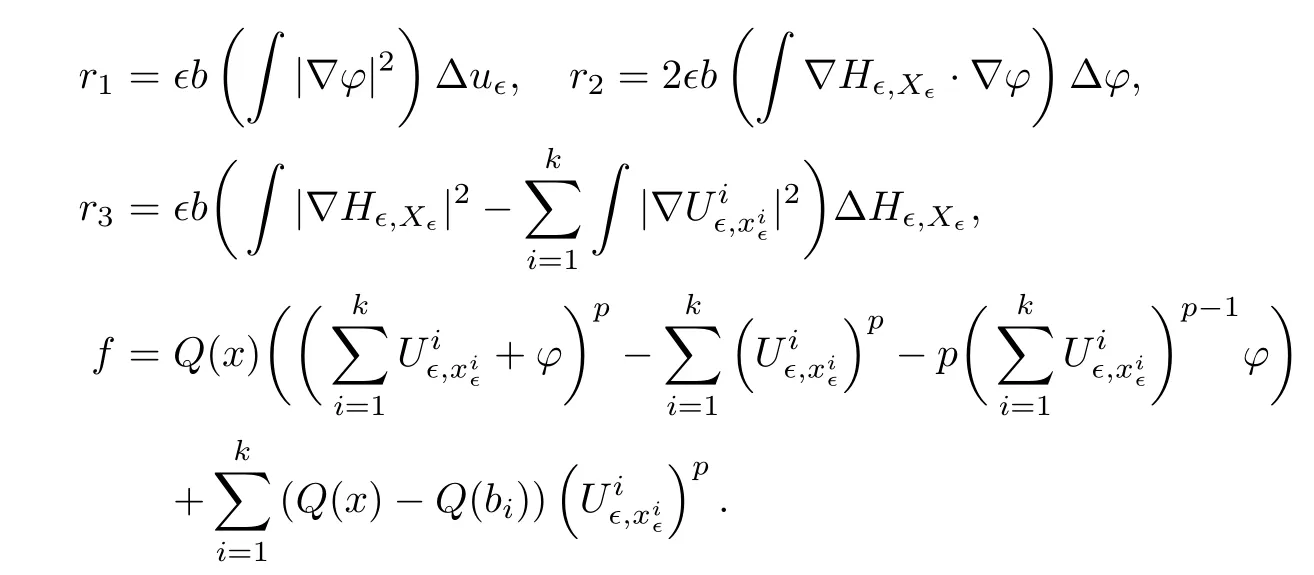









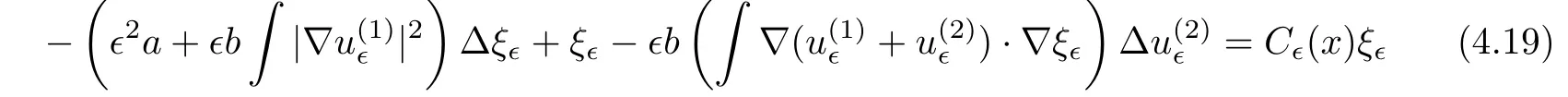





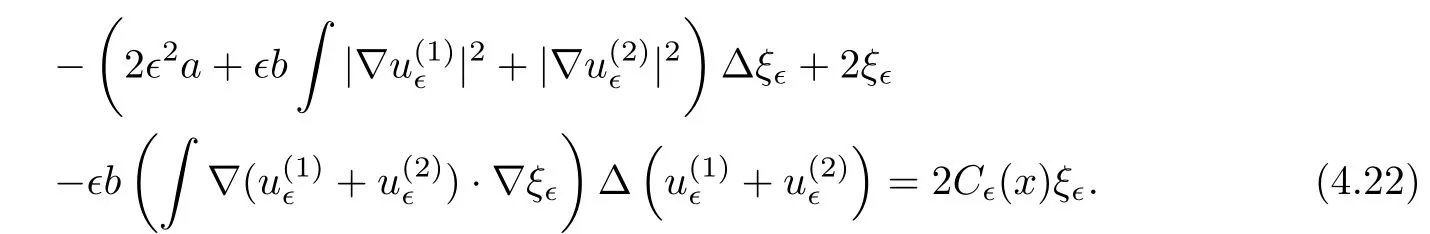
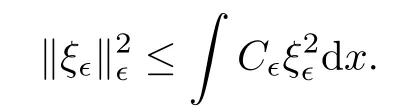
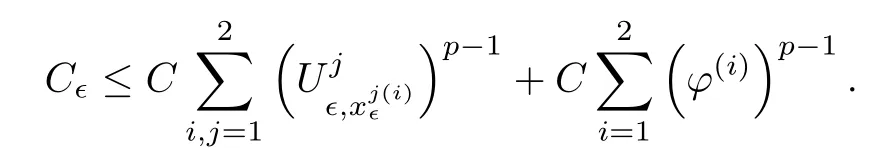

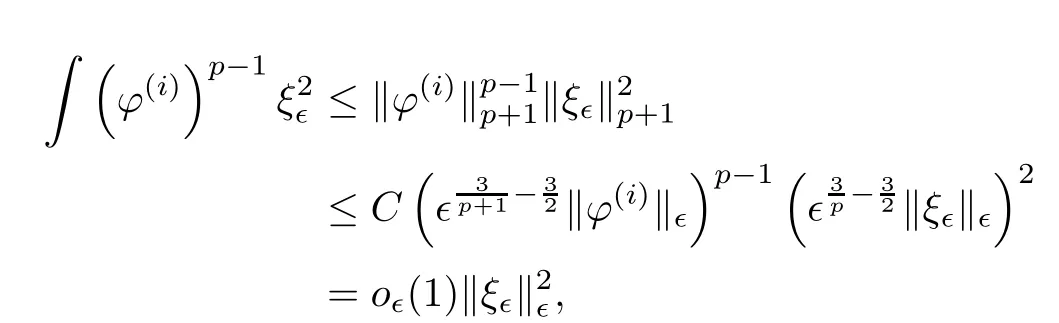



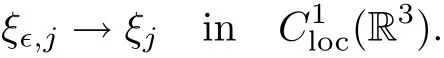




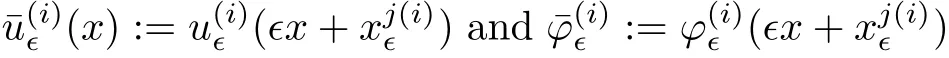



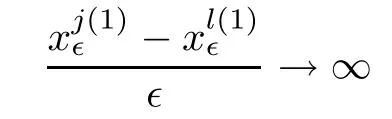

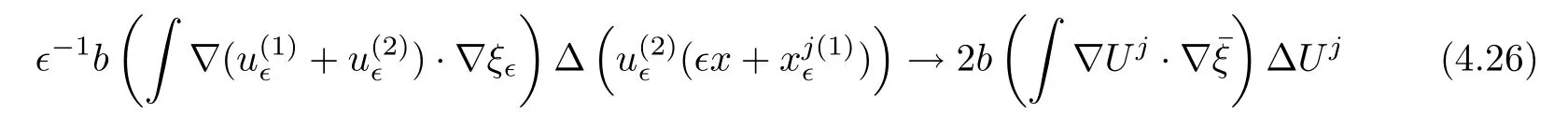



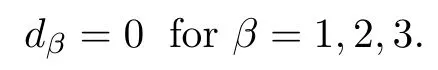
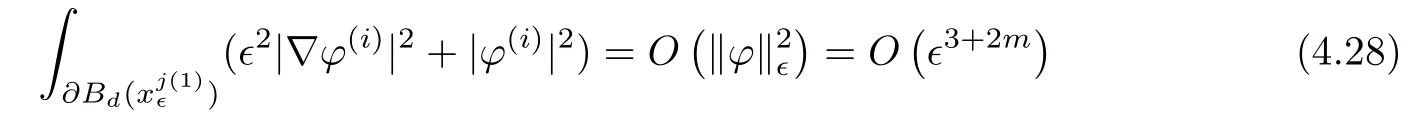




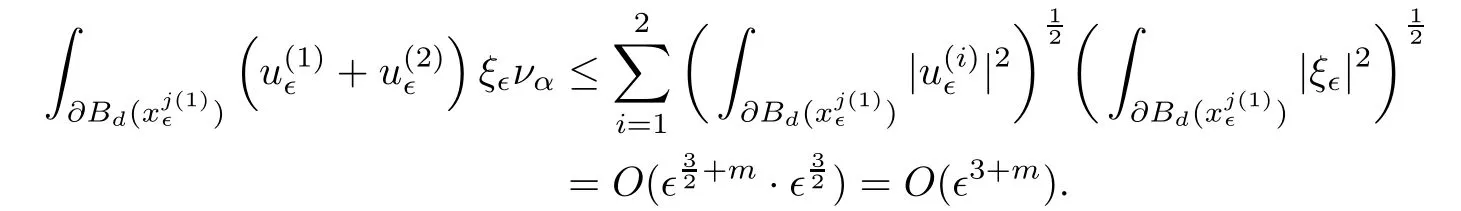

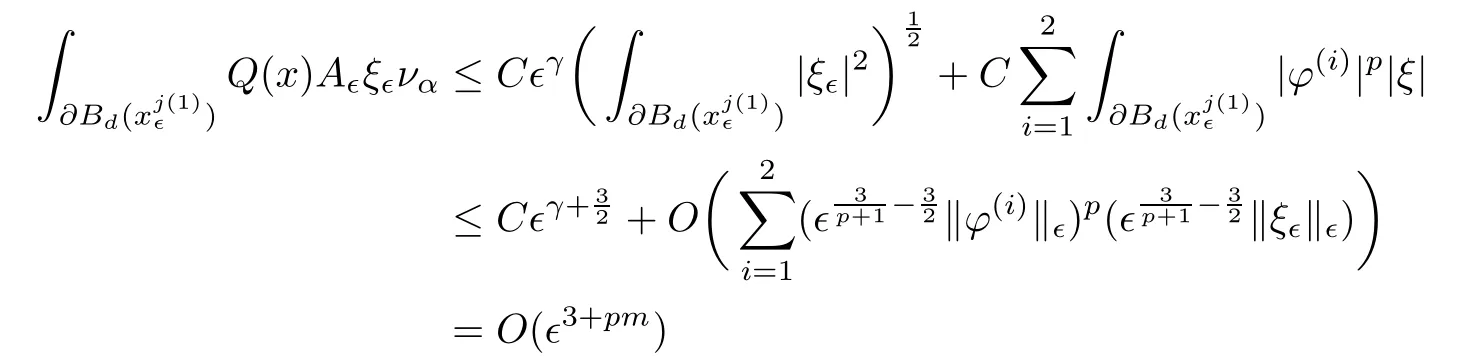



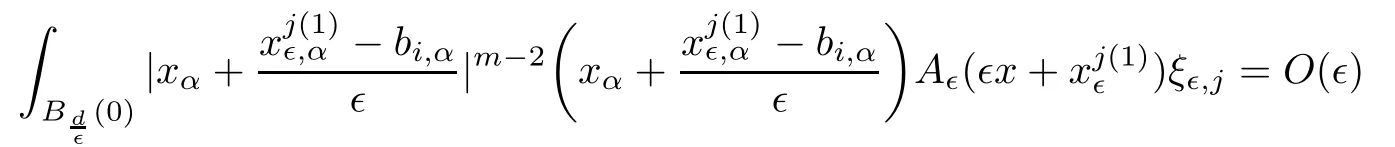
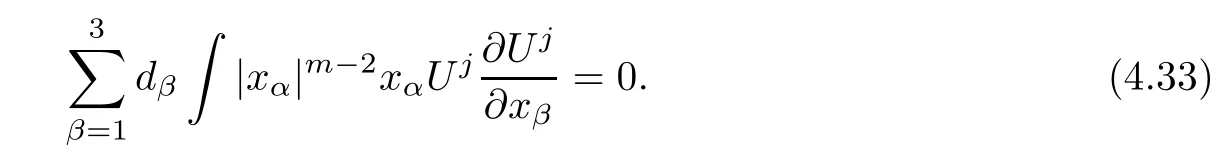
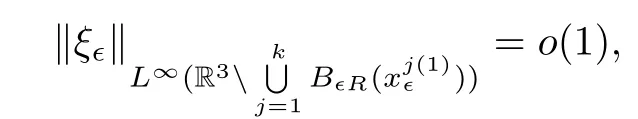




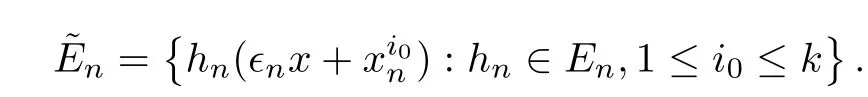



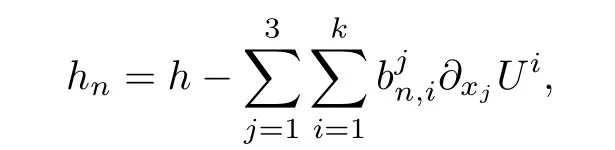







 Acta Mathematica Scientia(English Series)2020年1期
Acta Mathematica Scientia(English Series)2020年1期
