COMPLEX SYMMETRIC TOEPLITZ OPERATORS ON THE UNIT POLYDISK AND THE UNIT BALL∗

Cao JIANG(蒋操)

School of Mathematics and Information Sciences,Nanchang Hangkong University,Nanchang 330063,China

E-mail:jiangcc96@163.com

Xingtang DONG(董兴堂)†

School of Mathematics,Tianjin University,Tianjin 300350,China

E-mail:dongxingtang@163.com;dongxingtang@tju.edu.cn

Zehua ZHOU(周泽华)

School of Mathematics,Tianjin University,Tianjin 300350,China

E-mail:zehuazhoumath@aliyun.com;zhzhou@tju.edu.cn

Abstract In this article,we study complex symmetric Toeplitz operators on the Bergman space and the pluriharmonic Bergman space in several variables.Surprisingly,the necessary and sufficient conditions for Toeplitz operators to be complex symmetric on these two spaces with certain conjugations are just the same.Also,some interesting symmetry properties of complex symmetric Toeplitz operators are obtained.

Key words complex symmetric operator;Toeplitz operator;Bergman space;pluriharmonic Bergman space

1 Introduction

Let H be a complex separable Hilbert space.A conjugation on H is an anti-linear operator C:H→H such that C2=I and hCf,Cgi=hg,fi for all f,g∈H.A bounded linear operator T on H is said to be complex symmetric if there exists a conjugation C such that CT=T∗C.In this case,we say that T is complex symmetric with respect to C.

The general study of complex symmetric operators was initiated by Garcia and Putinar in[6].For any conjugation C on H,it is shown in[6]that there is an orthonormal basis{en}∞n=0for H such that Cen=en,n≥0.With this observation,an operator is complex symmetric precisely when it has a symmetric matrix representation under certain basis.Also,the class of complex symmetric operators turns to be quite diverse,which includes all normal operators,operators that are algebraic of order two,Hankel operators,compressed Toeplitz operators,and the Volterra integration operator.Over the past decade,numerous authors made signifi cant contributions to the study of complex symmetric operators;see[5,7–10,13,15,16]for example.

The problem of when a Toeplitz operator is complex symmetric on the classical Hardy space H2(D)was first studied by Guo and Zhu in[10].In a recent article[12],Ko and Lee provided a complete description of complex symmetric Toeplitz operators with the conjugation Cξ,θf(z)=on H2(D).The aim of this article is to obtain the corresponding results on the Bergman space and the pluriharmonic Bergman space over some n-dimension complex domains.

Let Dnbe the unit polydisk in the complex vector space Cn.For λ =(λ1,···,λn)with λj> −1,j=1,···,n,and z=(z1,···,zn)∈ Dn,we write

where dA denotes the normalized area measure on the unit disk D.

Another domain in Cnwe consider is the open unit ball Bn.We fi x a parameter t>−1 and consider the weighted volume measure on Bn

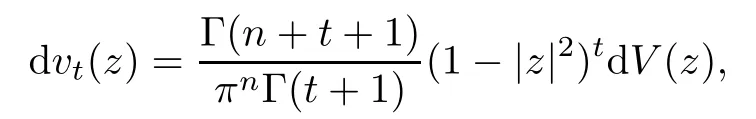
where dV denote the standard volume measure on Bn.

To simplify presentation throughout the article,we denote Ω as Dnor Bn,and let L2(Ω)be the square-integrable function spaces equipped with the corresponding weighted measure dvλor dvt.The Bergman space A2(Ω)is the closed subspace of L2(Ω)consisting of all holomorphic functions on Ω.Let P be the orthogonal projection from L2(Ω)onto A2(Ω).For a function u ∈ L∞(Ω),the Toeplitz operator Tuwith symbol u on A2(Ω)is de fined by Tu(f)=P(uf)for f ∈ A2(Ω).

The pluriharmonic Bergman space b2(Ω)is the closed subspace of L2(Ω),consisting of pluriharmonic functions.Because every pluriharmonic function on Ω can be expressed,uniquely up to an additive constant,as the sum of a holomorphic function and an antiholomorphic function,we see that b2(Ω)=A2(Ω)+Thus,the orthogonal projection Q from L2(Ω)onto b2(Ω)can be represented by Qf=Pf+−Pf(0).Then,the Toeplitz operatorwith symbol u on b2(Ω)is de fined by(f)=Q(uf)for f ∈ b2(Ω).

As we all know,every function ϕ ∈ L∞(Ω)has the polar decomposition

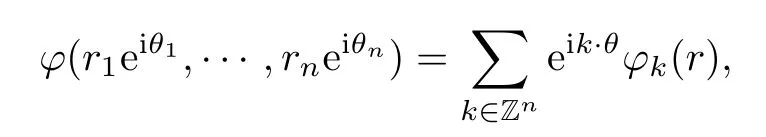
where k·θ=k1θ1+···+knθnand ϕk(r)= ϕk(r1,···,rn)are bounded separately radial functions on Ω.In particular,each component eik·θϕk(r)is called the quasihomogeneous function of degree k.See[1,2]for more details.

In this article,we fully concentrate on the following conjugation.For everyµ∈C with|µ|=1 and ζ=(ζ1,···,ζn) ∈ Rn,we de fine an operator Cµ,ζ:L2(Ω) → L2(Ω)by

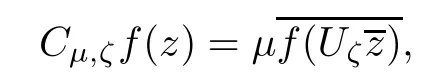
where Uζ=diag{eiζ1,···,eiζn}.It is easy to check that Cµ,ζis a conjugation on both A2(Ω)and b2(Ω).More precisely,both A2(Ω)and b2(Ω)reduce Cµ,ς.

Our first result gives a sufficient and necessary condition for Toeplitz operators to be complex symmetric with the conjugation Cµ,ζon A2(Ω)or on b2(Ω).Somewhat surprisingly,we find that there is no difference between the condition for Toeplitz operators to be complex symmetric with the conjugation Cµ,ζon A2(Ω)and that on b2(Ω).

Theorem 1.1Letbe a bounded function on Ω.Then the following statements are equivalent.

(b)Tϕis complex symmetric with respect to the conjugation Cµ,ζon A2(Ω).

(c) ϕ−k=eiζ·kϕkfor every k ∈ Zn.

When the parametersµ =1 and ζ=0,we simply write C1for Cµ,ζ,namely,C1f(z)=Ferreira[4]showed that every conjugation C on H2(D)is of type C=T∗C1T,where T is a topological linear isomorphism.So the conjugation C1plays an important role in the study of complex symmetric operators.As a consequence of Theorem 1.1,we obtain a conceptual condition for Toeplitz operators to be complex symmetric with the conjugation C1on A2(Ω)or on b2(Ω).

Corollary 1.2Let ϕ be a bounded function on Ω.Then the following statements are equivalent.

(b)Tϕis complex symmetric with respect to the conjugation C1on A2(Ω).

(c) ϕ(z)= ϕ(z).

From condition(c)of Theorem 1.1,we see that the polar decomposition for the symbol of the complex symmetric Toeplitz operator with the conjugation Cµ,ζon A2(Ω)has a symmetrical form.A natural question arises:for any complex symmetric Toeplitz operator Tϕon A2(Ω),does the condition ϕk(r)=0 imply that ϕ−k(r)=0 for any k ∈ Zn?It turns out that the answer is positive under certain conditions.To state our next result,we need the following notation.For a multi-index k=(k1,···,kn)∈ Zn,we write k?0 if kj≥ 0 for all j ∈ {1,···,n},and k?0 if ki<0 for some i∈ {1,···,n}.

Theorem 1.3Letbe a bounded function on Ω.If kerTϕ={0}on A2(Ω),then the following statements hold.

(a)Tϕis not complex symmetric on A2(Ω).

(b)Suppose that C is a conjugation on both A2(Ω)and b2(Ω).is not complex symmetric with respect to C on b2(Ω).

As direct consequences of Theorem 1.3,some interesting results concerning complex symmetric Toeplitz operators on the Bergman space are obtained:when n=1,Theorem 1.3 shows that a bounded function whose polar decomposition has only positive(or negative)components cannot deduce a nontrivial injective complex symmetric Toeplitz operator on A2(D);the Toeplitz operator with certain quasihomogeneous symbol on A2(Ω)is complex symmetric if and only if it is diagonal(see Corollaries 4.1 and 4.2);recall that[12,Theorem 2.1]shows that the complex symmetric analytic or co-analytic Toeplitz operator on H2(D)must be constant,we have a similar result for the Bergman space as follows.

Corollary 1.4Let ϕ be a bounded analytic or co-analytic function on Ω with ϕ(0)=0.If Tϕis a complex symmetric Toeplitz operator on A2(Ω),then ϕ is identically zero on Ω.

In addition,we would like to mention that the hypothesis for the conjugation C on condition(b)of Theorem 1.3 is necessary.Consider the ordinary complex conjugationon b2(Ω).Because the reproducing kernel of b2(Ω)is real-valued,it follows from the integral representation for the projection Q that=Q,hence

Therefore,all Toeplitz operators on b2(Ω)are complex symmetric with the conjugation

We end this introduction by mentioning that Toeplitz operators on the pluriharmonic Bergman space have special structure and enjoy some very interesting symmetry properties;see[3,11,14]for example.In this article,another symmetric property is discovered.Speci fically,a Toeplitz operatoris complex symmetric with the conjugation Cµ,ζon b2(Ω)if and only if Cµ,ζ=Cµ,ζwhen applied to the holomorphic part or the conjugate holomorphic part of the orthonormal basis for b2(Ω)(see Proposition 2.2).

2 Some Propositions

To study complex symmetric Toeplitz operators, first let us provide some important properties in this section.The first proposition establishes an interesting relationship of complex symmetric Toeplitz operator on A2(Ω)and that on b2(Ω).

Proposition 2.1Suppose C is a conjugation on both A2(Ω)and b2(Ω),and let ϕ be a bounded function on Ω.Ifis complex symmetric with respect to C on b2(Ω),then Tϕis also complex symmetric with respect to C on A2(Ω).

ProofFor each fixed α∈Nn,it is clear that

and

Recall that C is a conjugation on both A2(Ω)and b2(Ω).Thus,C[P(ϕwα)(z)]∈ A2(Ω),and

Hence,it follows from(2.1)that

which implies that

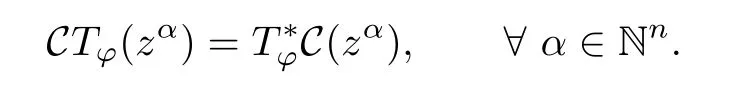
We next give the following proposition,which provides a critical symmetry property of complex symmetric Toeplitz operators with the conjugation Cµ,ζon b2(Ω).

Proposition 2.2Let ϕ be a bounded function on Ω.Then for any α ∈ Nn,

if and only if

ProofObserve that

We have

Acting Cµ,ζon both sides we have

Taking the conjugation on both sides of(2.3),we have

On the other hand,it is clear that

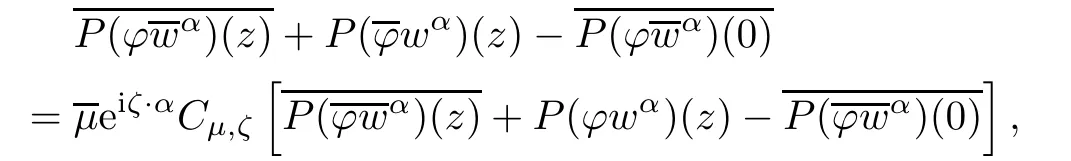
which is the same with(2.2)as,and.This completes the proof.

Lastly,let us take a review of the following classical proposition,which will be used in the next section.

Proposition 2.3Let f be a bounded holomorphic function onRezj> δj,j=1,···,n}for some δ=(δ1,···,δn) ∈ Nn.If there exists a positive integer N and a multi-index α0∈ Nnsuch that

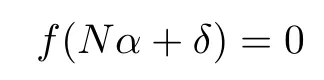
for all α ∈ Nnwith,then f is identically zero in

ProofThe proof is obvious from[1,Proposition 2.6].

3 Proof of Theorem 1.1

This section is devoted to the proof of Theorem 1.1.First we focus on the case when Ω is the unit polydisk Dn.One of the most useful tools in the following calculations shall be the Mellin transform.The Mellin transform bϕ of a separately radial function ϕ∈L1(Dn,dvλ)is de fined by the equation:

It is clear that bϕ is well de fined on{z∈Cn:Rezj≥2,j=1,···,n},and holomorphic on{z ∈ Cn:Rezj>2,j=1,···,n}.

Now we are ready to prove Theorem 1.1 in the case of the unit polydisk.

Proof of Theorem 1.1It follows from Proposition 2.1 that(a)implies(b).

To show that(b)implies(c),we fi x α∈Nn.Because the reproducing kernel of A2(Dn)is

we have

Replace k by −k and ϕkby.We arrive at

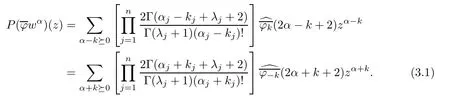
Recall that Cµ,ζ(zα)= µe−iζ·αzα.It follows that

and

As Tϕis complex symmetric with respect to Cµ,ζon A2(Dn),we have

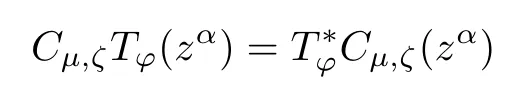
for any fi x α∈Nn.Combining this with the previous paragraph,we see that

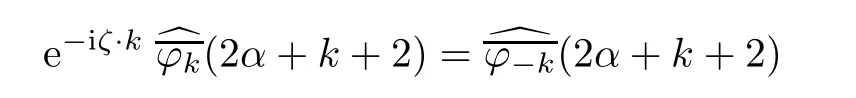
for all k ∈ Znwith α+k?0.Taking the conjugation on both sides,we obtain

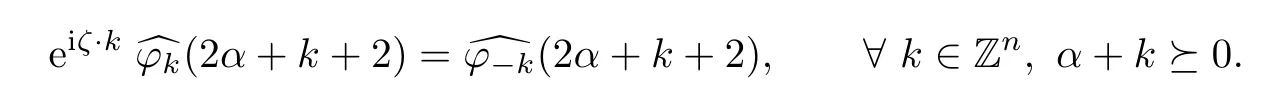
Then,for any fixed k∈Zn,we have

Consequently,eiζ·kϕk= ϕ−kfor each fixed k ∈ Znby Proposition 2.3,which shows that(b)implies(c).

To show that(c)implies(a),we also fi x α∈Nn.By a simple calculation,we obtain

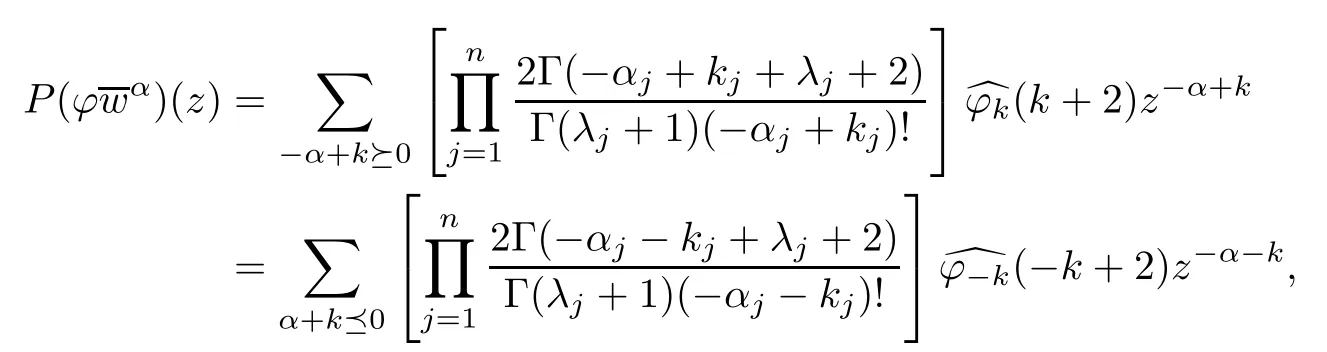
and

Recall that Cµ,ζ(zα)= µe−iζ·αzα,and=.It follows that

and

As ϕ−k=eiζ·kϕkfor every k ∈ Zn,we have

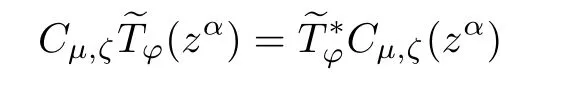
for each fixed α∈Nn.This together with Proposition 2.2 shows that(c)implies(a).

In the rest of this section,we focus on the case of the unit ball.In what follows,we will use the notation τ(Bn)for the base of the unit ball Bn,that is,

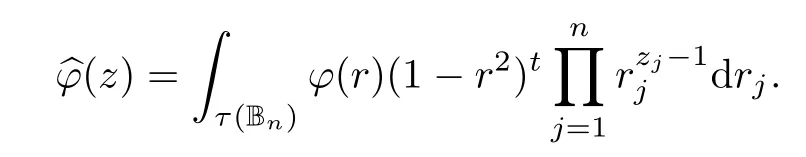
It is safe to use the same notationto denote the Mellin transform of a separately radial function on both Dnand Bn,as we always specify the space on which the operator Tϕacts.

Now fi x α ∈ Nn.For any β ∈ Nnon A2(Bn),we have

Then,applying formula(1.23)of[17],we have

and hence

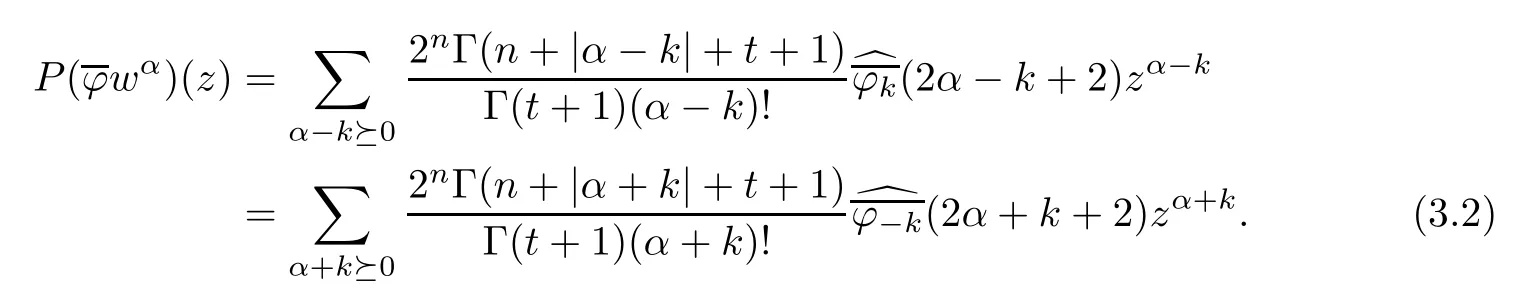
Using the similar argument,we obtain

and

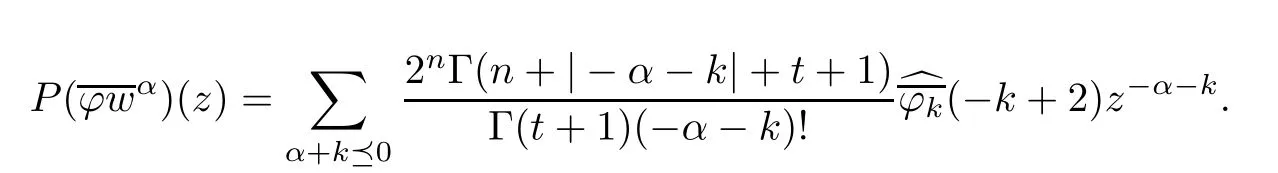
Therefore,Theorem 1.1 in the case of the unit ball can be proved by the same method as employed in the case of the unit polydisk.

4 Proof of Theorem 1.3

In this section,we will prove Theorem 1.3 and give some corollaries.

Proof of Theorem 1.3Without loss of generality,assume that

Then,it is clear from(3.1)and(3.2)that T∗ϕ(1)=P(ϕ)=0 on A2(Ω).

To prove(a),let us assume the contrary,namely,Tϕis complex symmetric with respect to some conjugation C on A2(Ω).Thus

Recall that the conjugation C is an isometric on A2(Ω),so TϕC(1)=0.As kerTϕ={0}on A2(Ω),it follows that C(1)=0.This contradicts the fact that C is an isometric on A2(Ω),then we completes the proof of(a).

Part(b)follows directly from(a)and Proposition 2.1.The proof of the theorem is now completed.

Consider the Toeplitz operators Teik·θϕkwith the quasihomogeneous symbols of degree k?0 on A2(Ω).For any fwe have Teik·θϕk(f)=0 if and only if

where Ck,αare nonzero constants.If we further assume that(β+2)6=0 for any β∈Nn,then it follows that kerTeik·θϕk={0}.Furthermore,it is easy to check that all Toeplitz operators with separately radial symbols are complex symmetric.Another application of Theorem 1.3 then gives the following result.

Corollary 4.1Let f=eik·θϕk(r)be a bounded quasihomogeneous function of degree k0 or k0 on Ω.If(α+2)6=0 for any α∈Nn,then Tfis complex symmetric on A2(Ω)if and only if it is a diagonal operator.

Because Mellin transforms of any nonzero separately radial monomial are never equal to zero,we obtain the following simple result about the complex symmetric monomial Toeplitz operators on A2(Ω).

Corollary 4.2The monomial Toeplitz operatorswith pq0 or qp0 are complex symmetric on A2(Ω)if and only if p=q.

When n=1,Corollary 4.2 implies that the monomial Toeplitz operatoris complex symmetric on A2(D)if and only if it is diagonal with respect to the standard monomial basis.In higher dimensions,the case p−q/∈Nn∪(−N)nremains an open problem.As a direct consequence of[3,Theorem A],the second author and Zhu gave a complete characterization of all normal monomial Toeplitz operators on A2(Bn),namely,is normal on A2(Bn)if and only if p=q.This together with Corollary 4.2 leads us to ask whether or not all complex symmetric monomial Toeplitz operators on A2(Ω)are normal.We leave this open for future research.