双变量协同的无人直升机发动机恒转速滑模控制

胡春明，魏石峰，刘 娜，宋玺娟，米 雪

双变量协同的无人直升机发动机恒转速滑模控制

胡春明1, 2，魏石峰2，刘 娜1，宋玺娟1，米 雪2

(1. 天津大学内燃机研究所，天津 300072；2. 天津大学机械工程学院，天津 300350)

针对无人直升机发动机恒转速控制问题，提出了一种油门/点火提前角双变量协同调节的恒转速滑模控制策略．发动机输出扭矩控制是恒转速控制问题关键的一环，而油门开度和点火提前角作为调节发动机输出扭矩的两个变量具有不同的特点．油门调节虽然调节范围宽，但是响应较慢，易受时滞效应的影响而产生超调现象；点火提前角响应较快，但是调节范围有限．将二者的优点结合起来实现协同控制，可以进一步加强恒转速控制效果．为实现此目的，对发动机进行了数学建模，并基于该模型和滑模控制设计了协同控制策略．该策略包括点火提前角优先调节的主逻辑和点火提前角回归逻辑．最终通过仿真和试验验证了控制策略的效果．仿真结果显示：负载突变时，双变量协同滑模控制器相较于传统PID控制器，转速误差减小61%；同样基于滑模控制，双变量协同控制相较于双变量分离控制，转速误差减小21.4%；存在负载扭矩干扰或进气压力波动时，双变量协同滑模控制的转速稳定性也优于其他两种控制方式；整机系留试验中，双变量协同滑模控制的转速波动范围比双变量分离滑模控制小24%，比传统PID控制小62%．经过多次系留试验观测，使用双变量协同滑模控制，可使转速波动范围在±70r/min以内，控制误差在2%以内，能够满足无人直升机飞行稳定性的要求．

双变量协同调节；滑模控制；发动机数学模型；恒转速控制；无人直升机

活塞式发动机具有油耗低、结构简单易维护、成本低等优点，在轻型、中小型、低空作业的无人直升机领域拥有很大的应用优势[1]．无人直升机主轴旋翼的转速控制精度直接影响其飞行安全及稳定性，而旋翼转速的稳定依赖于发动机转速的稳定，因此恒转速控制策略是设计无人直升机发动机控制器的第1要务[2]．活塞式发动机是一个典型的非线性、时滞性、随机性的系统[3]．针对非线性问题，文献[4]采用了模糊PID方法，文献[5]采用了神经网络PID方法，文献[6-7]采用了滑模控制方法；针对时滞性，文献[8]采用了Smith预测补偿方法，文献[9]采用了非线性模型预测控制方法；针对随机性，文献[3]采用了广义预测控制方法，文献[7]采用了鲁棒控制方法，文献[10]采用了自抗扰反馈控制方法．在这些无人直升机恒转速控制研究中，都没有考虑油门、点火提前角两个控制变量控制优先级的问题，而油门的调节范围宽但是响应慢，点火提前角的调节范围窄但是响应快[11-12]，通过设计一种点火提前角优先调节的双变量协同控制策略，将两者的优点有机结合，能够进一步优化转速稳定性．

本文对一款无人直升机的发动机进行了数学建模，并在模型和滑模控制的基础上提出了一种新型的油门/点火提前角双变量协同调节的控制策略，最后结合仿真和试验证明了控制策略的优越性．

1 发动机数学模型

建立研究对象的数学模型是设计控制器的基础．本文所研究的发动机为一台单缸四冲程汽油机，飞行时其目标转速恒定在6500r/min．其数学模型包括发动机进气通路模型、发动机扭矩输出模型、发动机转速模型．

1.1 发动机进气通路模型

进气通路模型描述了发动机的进气量、转速、油门开度、进气压力之间的关系．进气流量与转速和进气压力的关系由速度密度法[13]表示为

式中1、2为常数．

进气压力由油门开度和转速共同决定，对进气压力进行标定，建立进气压力与油门开度、转速对应关系的三维MAP，依此进行进气量计算．为了方便控制器中油门开度的反求，故建立油门开度关于进气压力和转速的三维MAP．综上，已知发动机油门开度和转速，可通过插值计算出进气压力．相反，如果得知发动机转速和进气压力，也可通过插值计算出油门开度，其表达式为

式中为油门开度，%．式(3)可用于进气量计算，式(4)可用于油门开度控制．

1.2 发动机扭矩输出模型

发动机扭矩输出模型描述了输出扭矩与进气量、过量空气系数、曲轴角速度、效率、机械损失扭矩之间的关系．效率由进气压力效率、点火提前角效率和过量空气系数效率3部分组成．输出扭矩表达式为

式中1、2、3均为常数．

1.3 发动机转速模型

发动机作为无人直升机动力系统的动力源，给无人直升机输出扭矩，无人直升机的旋翼及主轴作为负载，输出扭矩与负载扭矩共同决定发动机的转速．此系统可以表示为

(14)

式中：load为发动机负载扭矩，N·m；为无人直升机动力系统整体的转动惯量，kg·m2．恒转速控制过程中，转速基本稳定，负载扭矩load主要由旋翼桨距决定，两者之间的关系通过一维MAP表示为

1.4 总体模型与参数辨识结果

结合式(11)和式(14)，无人直升机发动机的总体模型为

上述模型中包含若干待定参数，根据大量的发动机试验数据对待定参数进行优化辨识，形成最终的数学模型．辨识结果如表1所示．

表1 模型参数辨识结果

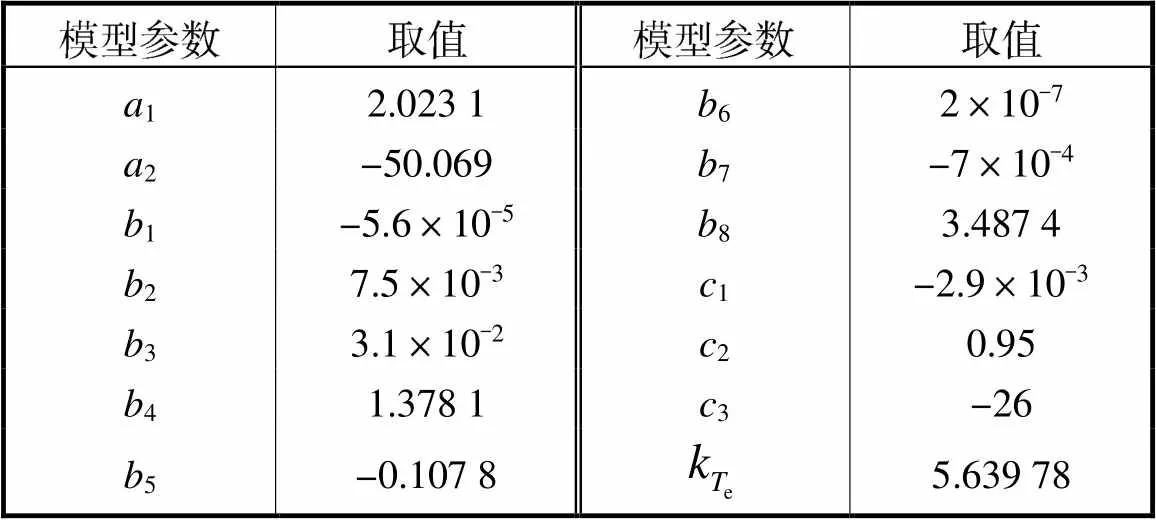
Tab.1 Identification results of the model parameters

在MATLAB/Simulink仿真软件下搭建发动机数学模型，并将仿真结果与试验结果进行对比．如图1所示，6500r/min工况下发动机输出扭矩的仿真值与试验值之间拟合精度较高，最大误差为3.4%．

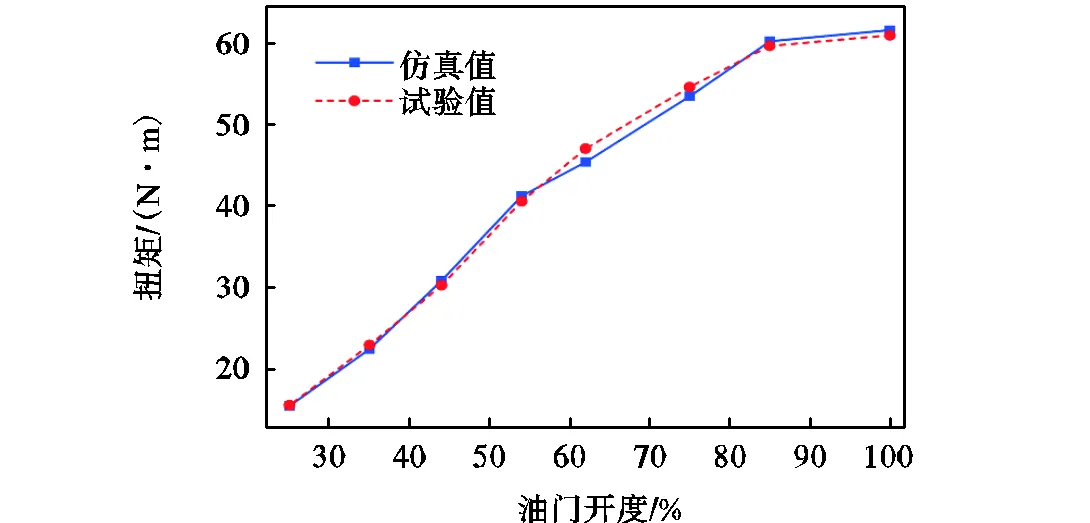
图1 仿真值与试验值对比

2 恒转速控制器设计

2.1 控制器逻辑的提出

2.1.1 研究背景

图2所示为目前无人直升机普遍采用的传统PID恒转速控制器，当转速存在误差时，油门和点火提前角同时调整，由于油门调节范围比点火提前角大，因此油门调节起主导作用，点火提前角调节起辅助作用．一般为保证大扰动下的调节能力，油门反馈增益取值较大，但负载扭矩趋于稳定时，油门调节程度仍较大，会造成转速波动．虽然此问题可以通过变增益系数的方式优化，但是标定难度较大．为充分利用点火提前角响应快、调节精度较高的特点，可对这两个控制变量进行优先级划分．

图2 无人直升机发动机传统PID恒转速控制器

面对双变量控制优先级的问题，在过程控制领域有一种成熟的控制策略——Mid-Ranging，目前该方法已应用在发动机怠速转速控制当中[11-12]，其原理如图3所示，根据转速误差先进行点火提前角调节；检测到点火提前角偏离标称值时，油门再进行调节．但是由于无人直升机发动机的负载扭矩变化剧烈，有时油门需要立即进行调节而不等待点火提前角的反馈调节，因此Mid-Ranging的思想不适用于无人直升机发动机恒转速控制，需设计一种更加灵活的双变量协同方式，根据目标输出扭矩的大小决定调节方式．

图3 Mid-Ranging发动机转速控制策略

2.1.2 双变量协同的滑模控制

笔者基于滑模提出了一种油门/点火提前角双变量协同调节的发动机转速控制策略．如图4所示，总体控制逻辑分为基于滑模控制的主逻辑和点火提前角回归逻辑．主逻辑中，滑模控制根据转速误差和负载扭矩计算目标输出扭矩．根据目标输出扭矩和当前发动机输出扭矩状态量评估仅调节点火提前角能否达到目标输出扭矩，如果可以，则计算点火提前角调整量，若不可以，则执行最大的点火提前角调整量，并计算油门补充调节量以达到目标输出扭矩，从而实现点火提前角优先调节．

主逻辑的调用频率为目标输出扭矩改变的频率，受系统惯性的影响其值不能过快，根据试验优化结果，主逻辑的调用时间为100ms较为合适．在主逻辑调用之后需将点火提前角逐渐调整为标称值以保证点火提前角调节能力，并在此期间调整油门开度保证输出扭矩不变．这个逻辑称为点火提前角回归逻辑．由于额定转速在6500r/min附近，两次做功间隔约为20ms，因此设置该逻辑20ms调用一次．

图4 油门/点火提前角协同调节发动机恒转速滑模控制逻辑

2.2 控制器设计

2.2.1 主逻辑

采用滑模控制计算目标输出扭矩，首先根据控制目标设计输出误差，即

式中：为输出误差；d为目标角速度．

为分配油门和点火提前角的调节量，设计系统输入为

代入式(16)，系统状态方程为

设计滑模面的特性如下：

式中1、2、为常数，且＞0．选择李雅普诺夫函数进行稳定性判定，即

因为＞0，显然式(23)成立，满足滑动模态的到达性条件，系统是稳定的．由式(19)～(21)可推导出系统输入的控制率为

控制器总体结构如图5所示，系统输入实际上并不是执行器的直接输出，它包含了油门调节和点火提前角调节在发动机输出扭矩中的共同作用．接下来介绍已知的控制率后，油门和点火提前角的具体分配方式．

图5 控制器总体结构

通过式(18)的发动机模型计算当前时刻发动机的输入状态量，用表示，再计算的调节倍数K，

式中()为(i)的反函数．在i的取值范围内，该反函数表达式为

2.2.2 点火提前角回归逻辑

点火提前角回归逻辑的任务是将点火提前角逐渐向标称点火提前角靠拢，以保证下次调节时点火提前角的调整能力．同时计算油门开度调整量以消除点火提前角回归带来的扭矩变化，期间油门缓慢动作，相当于把1次油门动作分解为4次，减弱了时滞效应的影响．点火提前角回归的输出为目标点火提前角和目标油门开度，具体表达式为

3 仿真及试验结果

3.1 仿真结果

在MATLAB/Simulink仿真环境下搭建发动机模型及控制器，仿真对比双变量协同滑模控制器和图3所示的传统PID控制器的转速稳定性．传统PID控制器的3个增益系数用P、I、D来表示，油门PID反馈和点火提前角PID反馈调用的周期不同，根据优化调整，最终取值如表2所示．

表2 传统PID控制器的参数取值

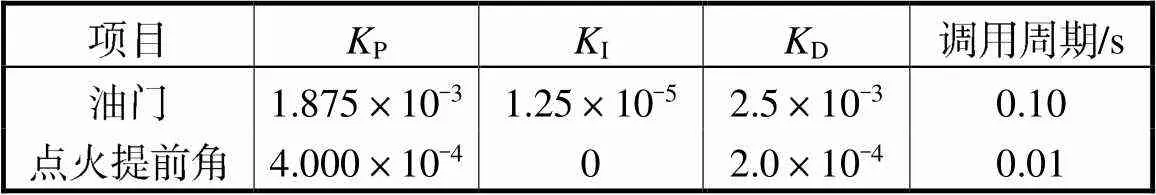
Tab.2 Parameter values of traditional PID controller

如图6所示，模拟无人直升机飞行和受扰动的情况，旋翼桨距经历突增突降和快速抖振的过程．可以看出双变量协同控制器的点火提前角调节比传统控制更快速，当需用扭矩变化时，点火提前角的快速调节可以及时调整输出扭矩，同时油门也随之响应．油门开度相较于传统控制器能够快速稳定在平衡点，超调量小．最终双变量协同控制器相较传统控制器，转速误差最大减小61%．

图6 双变量协同滑模控制与传统PID控制的对比

上述对比说明了本文提出的控制器整体性能较好，但是其中包含了滑模控制在非线性问题上相较于传统PID控制的优越性．为了单独验证双变量协同调节机制的优越性，设计了一种基于滑模的双变量分离控制器，即在双变量协同控制器的基础上，将目标输出扭矩值直接转化为油门调节量，而点火提前角由转速误差PID反馈来修正，这样的控制器油门/点火提前角的控制回路是分离的．仿真对比时控制器中相同部分的参数保持不变．

图7对比了双变量协同调节与双变量分离调节的控制效果，双变量协同调节的点火提前角调节更加频繁快速，发挥了其响应迅速的优点，同时油门开度的变化更加缓和，最终转速误差减小了21.4%．

图7 双变量协同滑模控制与双变量分离滑模控制对比

前述的仿真算例都是通过改变旋翼桨距来改变负载扭矩，而在无人直升机运行过程中，随机出现的负载扭矩干扰也是改变负载扭矩的重要因素．同时，发动机输出扭矩受到随机性的影响也会出现波动，最具代表性的就是进气过程的随机性．因此，设计了负载扭矩干扰和进气过程中的进气压力波动两种仿真算例，从而验证控制器的稳定性和适应性．

设置负载扭矩干扰在±3N·m内随机波动，且干扰信号采样周期为0.1s．仿真过程中旋翼桨距保持不变，负载扭矩只受负载扭矩干扰的影响．图8所示为3种控制方式在负载扭矩干扰下的转速波动情况．双变量协同滑模控制相较于其他两种控制方式，转速波动更小．

图8 存在负载扭矩干扰的仿真结果

根据经验设置进气压力干扰在±3kPa内随机波动，采样周期为0.1s．进气压力由油门开度和进气压力波动共同决定．图9所示为3种控制方式在进气压力波动下的转速波动情况．双变量协同滑模控制相较于其他两种控制方式，转速波动更小．

存在负载扭矩干扰和进气压力波动时的仿真结果表明，双变量协同滑模控制的点火提前角优先调节原则，可以有效增加系统的动力响应性；又因为滑模控制本身的鲁棒性强，使得控制器具有较好的抗扰动能力．

3.2 试验结果

将上述双变量协同转速控制器嵌入到无人直升机发动机ECU内，进行无人直升机的地面整机系留试验．无人直升机系留试验装置如图10所示，无人直升机固定在地面上，飞控系统和发动机ECU搭载在无人直升机上，由遥控和地面站进行飞行意图的远程操控．飞控系统可改变桨距，发动机ECU控制发动机转速．运行过程中的桨距、转速、油门开度等信息会保存下来以供分析．

图11所示的旋翼桨距变化过程是参考无人直升机恶劣飞行条件下的操作情况而制定的．将该旋翼桨距变化过程固化在飞控系统中，分别使用双变量协同滑模控制、双变量分离滑模控制、传统PID控制进行3次相同的系留试验．

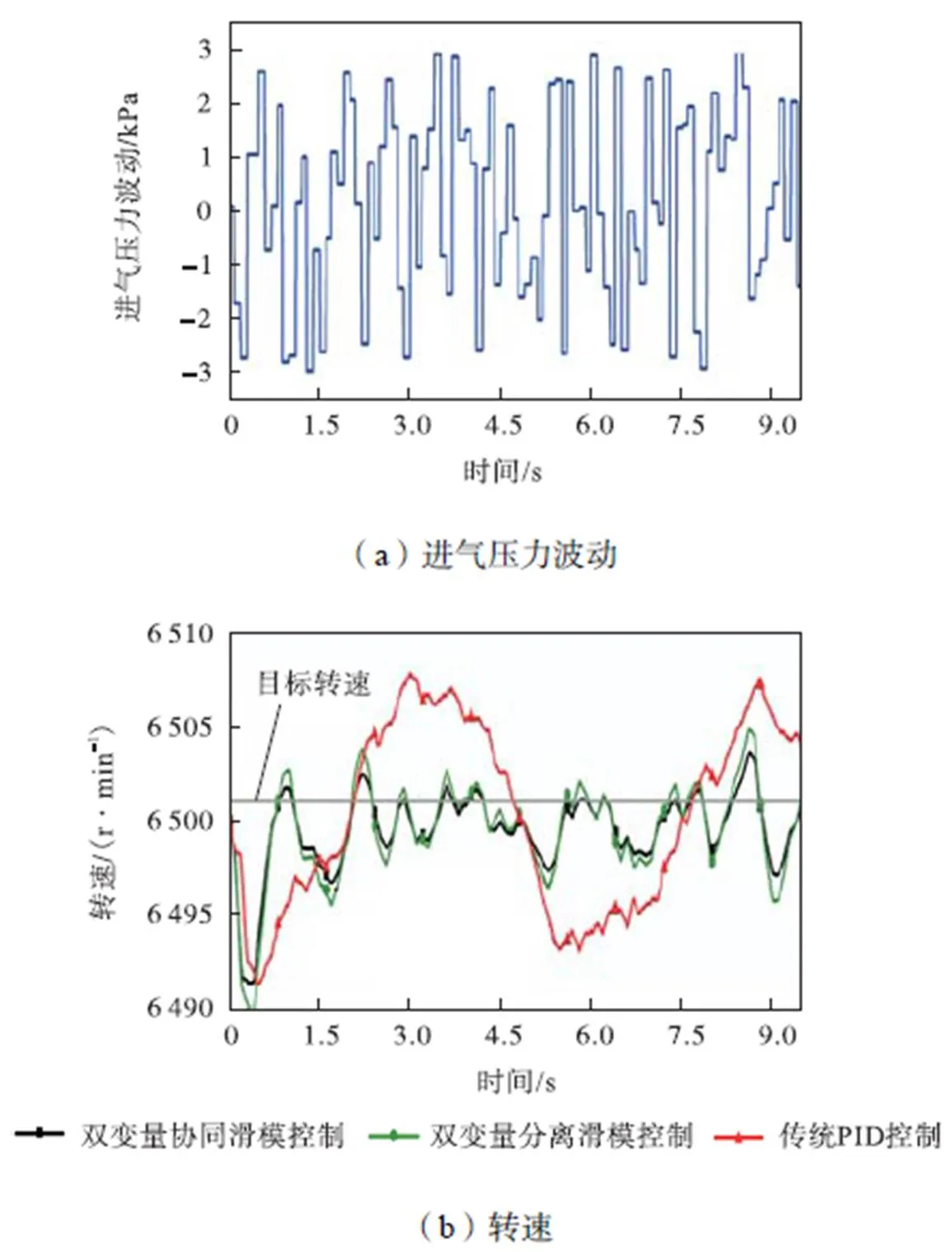
图9 存在进气压力波动的仿真结果

图10 无人直升机系留试验装置

在发动机转速到达6500r/min之后，恒转速控制器开始工作．图11展示了3种控制方式的转速波动情况．在恒转速工作区间，双变量协同滑模控制的转速在6444.7～6568.8r/min以内波动；双变量分离滑模控制的转速在6442.2～6606.2r/min以内波动；传统PID控制的转速在6341.9～6668.3r/min以内波动．

双变量协同滑模控制相较于双变量分离滑模控制，转速波动减小24%；相较于传统PID控制，转速波动减小62%．经过多次系留试验观测，使用双变量协同滑模控制，可使转速波动在±70r/min以内，即控制误差在2%以内，能够满足无人直升机飞行稳定性的要求．

图11 试验结果

4 结 论

(1) 建立了无人直升机发动机的数学模型，通过试验数据进行了参数辨识和验证，6500r/min工况下发动机输出扭矩的模型计算值与实测值之间拟合精度较高，最大误差为3.4%．

(2) 设计了基于滑模的油门/点火提前角双变量协同控制主逻辑以及点火提前角回归逻辑，将点火提前角响应快和油门调节范围宽的优点结合起来，从而进一步增强恒转速控制效果．

(3) 仿真结果表明：双变量协同滑模控制可使得点火提前角的调节更加迅速，油门调节更加缓和．其相较于传统PID控制，转速误差减小61%；相较于双变量分离调节方式，转速误差减小21.4%．存在负载扭矩干扰和进气压力波动时，双变量协同滑模控制相较于其他两种控制方式具有更好的稳定性．

(4) 无人机整机系留试验结果表明：在相同的测试循环下，双变量协同滑模控制相较于其他两种控制方式，转速波动更小．经多次试验观测，使用双变量协同滑模控制，可使转速波动在±70r/min以内，即控制误差在2%以内，能够满足无人直升机飞行稳定性的要求．

［1］ 王晓滕. 无人直升机用活塞式发动机技术发展现状与趋势[C]// 内燃机科技(企业篇)——中国内燃机学会第六届青年学术年会论文集. 杭州，中国，2015：358-361.

Wang Xiaoteng. Development status and trend of piston UAV engine technology[C]//Internal Combustion Engine Technology(Enterprise Chapter)—Proceedings of the 6th Annual Youth Academic Meeting of China Internal Combustion Engine Society. Hangzhou，China，2015：358-361(in Chinese).

［2］ 曾国贵，廖智麟，阚兆成. 某型无人直升机活塞式电喷发动机转速控制设计及试验[J]. 航空动力学报，2011，26(6)：1384-1388.

Zeng Guogui，Liao Zhilin，Kan Zhaocheng. Speed control design and test for piston EFI engine of unmanned helicopter[J]. Journal of Aerospace Power，2011，26(6)：1384-1388(in Chinese).

［3］ 陈林林，魏民祥，邵金菊. 无人直升机发动机恒转速广义预测控制[J]. 电子科技大学学报，2010，39(3)：475-480.

Chen Linlin，Wei Minxiang，Shao Jinju. Generalized predictive controller design for an unmanned helicopter engine speed[J]. Journal of University of Electronic Science and Technology of China，2010，39(3)：475-480(in Chinese).

［4］ 乔伯真，缑林峰. 模糊自整定PID的航空发动机转速控制研究[J]. 计算机仿真，2013，30(4)：63-67.

Qiao Bozhen，Gou Linfeng. Rotating speed based on fuzzy control for aero-engine self-tuning PID controller[J]. Computer Simulation，2013，30(4)：63-67(in Chinese).

［5］ 邢科龙，暨仲明. 基于神经网络PID的发动机转速控制系统[J]. 工业控制计算机，2015，28(11)：66-67.

Xing Kelong，Ji Zhongming. System of engine speed control based on neural network PID[J]. Industrial Control Computer，2015，28(11)：66-67(in Chinese).

［6］ 赵松涛. 小型无人直升机发动机控制系统研究与设计[D]. 广州：华南理工大学，2015.

Zhao Songtao. Research and Design of the Engine Control System for Small Scale UAV[D]. Guangzhou：South China University of Technology，2015(in Chinese).

［7］ 王 莉，刘德新. 稀燃汽油机空燃比滑模-神经网络控制及实验[J]. 天津大学学报，2006，39(增1)：51-56.

Wang Li，Liu Dexin. Sliding mode-neural network control for air-fuel ratio of lean burn gasoline engine and experiment research[J]. Journal of Tianjin University，2006，39(Suppl 1)：51-56(in Chinese).

［8］ Hong Jinlong，Gao Bingzhao，Lü Liang，et al. Engine speed control during gear shifting of AMT HEVs with identified intake-to-power delay[J]. IFAC Papers on Line，2016，49(11)：793-799.

［9］ Puleston P F，Spurgeon S，Monsees G. Automotive engine speed control：A robust nonlinear control framework[J]. IEEE Proceedings - Control Theory and Applications，2001，148(1)：81-87.

［10］ Tibola J R，Lanzanova T D M，Martins M E S，et al. Modeling and speed control design of an ethanol engine for variable speed gensets[J]. Control Engineering Practice，2015，35：54-66.

［11］ Solyom S，Eriksson S. Mid-ranging scheme for idle speed control of SI engines[C]// SAE Technical Paper. Detroit，USA，2006：2006-01-0608.

［12］ Huang X，Xie H，Song K. Idle speed control of FSAE racing engines based on mid-ranging ADRC[C]// Proceedings of the 33rd Chinese Control Conference. Nanjing，China，2014：201-206.

［13］ 王 莉，刘鲁源，刘德新，等. 基于控制的稀薄燃烧汽油机进气模型[J]. 天津大学学报，2005，38(3)：201-205.

Wang Li，Liu Luyuan，Liu Dexin，et al. Control based intake airflow dynamics model of lean burn gasoline engine[J]. Journal of Tianjin University，2005，38(3)：201-205(in Chinese).

［14］ 赵 华，宁锦标，谢 辉，等. 用于柴油机扭矩控制的摩擦扭矩在线修正算法[J]. 天津大学学报：自然科学与工程技术版，2014，47(10)：849-855.

Zhao Hua，Ning Jinbiao，Xie Hui，et al. On-line correction algorithm of friction torque for diesel engine torque control[J]. Journal of Tianjin University：Science and Technology，2014，47(10)：849-855(in Chinese).

［15］ Chevalier A，Müller M，Hendricks E. On the validity of mean value engine models during transient operation[J]. SAE Transactions，2000，109(3)：1571-1592.

Bivariate Coordinated Sliding Mode Constant Speed Controller for an Unmanned Helicopter Engine

Hu Chunming1, 2，Wei Shifeng2，Liu Na1，Song Xijuan1，Mi Xue2

(1. Tianjin Internal Combustion Engine Research Institute，Tianjin University，Tianjin 300072，China；2. School of Mechanical Engineering，Tianjin University，Tianjin 300350，China)

The constant speed control of unmanned helicopter engines is important．To address this issue，a bivariate coordinated sliding mode constant speed controller is proposed．In this study，bivariate refers to throttle opening and ignition advance angle．Notably，throttle opening and ignition advance angle，as two important variables for adjusting engine torque，have different characteristics．Throttle opening has a wide adjustment range but a slow responsiveness，which makes it susceptible to overshoot by the effects of time delay．By contrast，ignition advance angle has a narrow adjustment range but a fast responsiveness．If the advantages of these two variables are combined，then the constant speed control effect could be further enhanced．For this purpose，the engine was mathematically modeled．On the basis of the model of sliding mode control，a bivariate coordinated control strategy was designed．The strategy includes a master logic，spark advance angle priority adjustment based on sliding mode，and spark advance angle regression logic．Finally，the effect of the control strategy was verified by simulation and experiment．The simulation results showed that，when the load changes abruptly，the bivariate coordinated sliding mode controller reduces the speed error by 61% compared with the traditional PID controller．Furthermore，on the basis of sliding mode control，the bivariate coordinated controller reduces the speed error by 21.4% compared with the bivariate separated controller．Moreover，when the load and intake disturbance is simulated，the proposed controller has better anti-interference capability than the two other controllers．Finally，the results of the helicopter mooring experiment showed that the speed fluctuation range of the bivariate coordinated sliding mode controller is 24% smaller than that of the bivariate separated sliding mode controller and 62% smaller than that of the traditional PID controller．The results of multiple experiments showed that the speed fluctuation range is within ±70r/min using the bivariate coordinated sliding mode controller．The error is within 2%，which satisfies the flight stability requirements for unmanned helicopters．

bivariate coordinated regulation；sliding mode control；mathematical model of engine；constant speed control；unmanned helicopter

Supported by the National Natural Science Foundation of China(No.51476112).

V233.742

A

0493-2137(2020)05-0483-09

10.11784/tdxbz201907020

2019-07-07；

2019-08-12.

胡春明（1967—  ），男，博士，研究员.

胡春明，cmhu@tju.edu.cn.

国家自然科学基金资助项目(51476112).

(责任编辑：金顺爱)