基于MEMS加速度传感器的位移测量系统
牛伟萌,房立清,齐子元,郭德卿
(陆军工程大学石家庄校区火炮工程系,河北石家庄 050003)
0 引言
随着 MEMS(微机电系统)技术的不断发展,MEMS传感器正以其高性能、高稳定性、低功耗、小体积等优势广泛应用于运动载体姿态测量中,如车载导航、精确制导、卫星发射等[1-2]。在位移测量方面,一般采取的方式是雷达测试、光学测试和高速摄影等[3-4]。这些技术发展到现阶段,测量精度基本都比较高,是实现位移测量行之有效的方法,但是对于外界工作环境的依赖使系统的自适应能力和智能化水平受到了限制。由于加速度是一个易于测量的物理量,使用加速度信号进行位移解算一直是人们研究的热点[5],国内外对于积分算法进行了大量的研究,文献[6]使用最小二乘的多项式拟合方法消除趋势项误差,取得了十分良好的效果。文献[7]设计了移动窗截取相邻3个采样点进行Lagrange多项式拟合的积分法,在不损失采样频率的情况下提高了精度。文献[8]针对时域积分和频域积分的特点,设计了一种混合积分算法控制二次积分的累积误差。但这些位移解算大多是针对振动、变形的微小位移,并且没有集成化为完整的测量系统。本文以加速度传感器位移控制原理为基础,设计了一种适用于较长距离的位移测量系统,采用MEMS加速度传感器精确获得运动载体加速度,设计了加速度数值积分的多项式拟合算法减小误差,在直线导轨运动平台上进行了位移测试实验,实验表明该位移测量系统精度较高,位移测量误差最大为1.6%,最小可达0.3%,在误差允许的范围内满足工程化应用的要求,可适用于军事导航控制系统以及生活消费方面的位移测量控制。
1 加速度传感器位移测量控制原理
实际应用中通过加速度信号进行积分解算位移时,获得的加速度数据是一组离散值,当n>1时,在离散域中
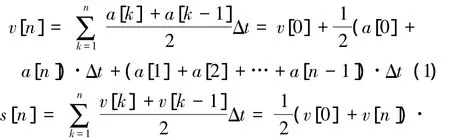
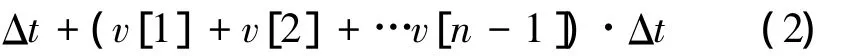
式中:a[n]为第 n 时刻的加速度读值;v[n]、s[n]为对应时刻的速度、位移值。
根据式(1)、式(2)可以得出目标物体在n时刻单方向的移动位移为

从式(3)可以得出,只需获知运动载体的初始速度v[0],结合MEMS加速度传感器输出的实时加速度便可求出目标物体的实时位移结果。在实际的处理算法中,为了避免n值增大时给处理器带来的巨大运算量,降低运行内存,避免重复运算,采用迭代方法简化运算过程。根据式(1)得:

将式(4)、式(5)改写为

从式(6)、式(7)可以得出,利用上一次的测量加速度 a[n-1]和运算结果 v[n-1]、s[n-1],以及实时测量加速度a[n],就可以求出物体的实时运动位移s[n]和实时运动速度 v[n]。
2 系统算法设计
系统算法设计以位移测量控制原理为基础,针对积分解算误差加入了加速度修正算法。具体分析和设计如下。
2.1 测量误差分析
在工程实际中,加速度信号包含环境中的各种干扰信号,直接进行时域积分会产生严重的趋势项误差[11],趋势项的误差来源于干扰信号会在加速度采集过程中产生直流误差项ε,因此实际测得的加速度应该为

经过时域的一次积分得到的速度信号和两次积分得到的位移信号分别为
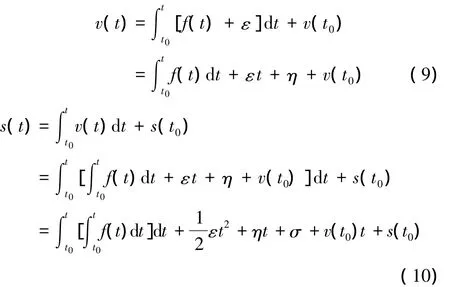
式中:ε为加速度信号的直流分量;η为第一次积分产生的常数项误差;σ为第二次积分产生的常数项误差。
在离散域积分中,实际速度和位移信号就变为
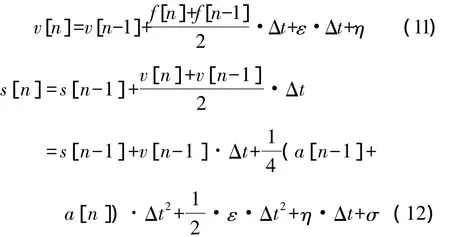
由式(2)可知,每积分一次,常数项ε、η、σ造成的趋势项误差都会指数倍放大。一次积分得到速度时出现一次趋势项误差ε·Δt+η,二次积分得到位移时会出现二次趋势项误差且迭代算法中初始的微小误差会随着迭代次数的增加而不断增大。
为解决上述问题,本文采用多项式拟合趋势项的方法去除积分过程中产生一次误差和二次误差,提高位移测量精度。
2.2 加速度修正算法设计
2.2.1 多项式拟合算法
根据测量得到的加速度信号,利用梯形公式进行数值积分得到速度信号和位移信号:

假设存在多项式ym(t),使得vi,si之间的差值平方和最小,利用最小二乘法拟合出趋势项误差:

式中:m为最高次项系数;pk为多项式系数;φ为最高次项不超过m的多项式集合。
从而得出如下方程式:

由式(15)可知,只要找出一组系数pk,使得函数I取得最小值,就可以确定积分趋势项。根据多元函数取极值的条件可得:

即

利用矩形公式表示为

可以证明,式(18)中系数矩阵是正定矩阵,存在唯一解,解出pk就可以求出多项式ym(t)进而可得到该算法下的加速度信号以及对应的速度和位移信号:
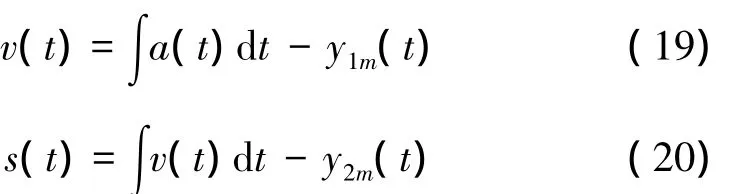
2.2.2 加速度修正算法
加速度传感器在使用过程中不可避免地会受到温度的影响,并且存在零点偏移,采用非线性特性的加速度值修正算法,将温度误差补偿at和零点漂移补偿ac统一到Δa中,即
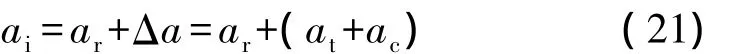
式中:ai,ar分别为加速度的理想输出值和实际输出值。
观察式(21)可发现,实际的补偿可以看成一个常数值,因此进行理想值计算时可以构建几何关系:

将式(22)进行变换可得:

因此只需要知道k值就可以完成对零点漂移和温度的双向补偿。在进行k值求取的过程中,设修正的加速度即测量加速度为 ar[j](j=1,2,3,…,n),所对应的精确值为 ai[j](j=1,2,3,…,n)。根据式(2)可得

代入式(11)、式(12)可得:
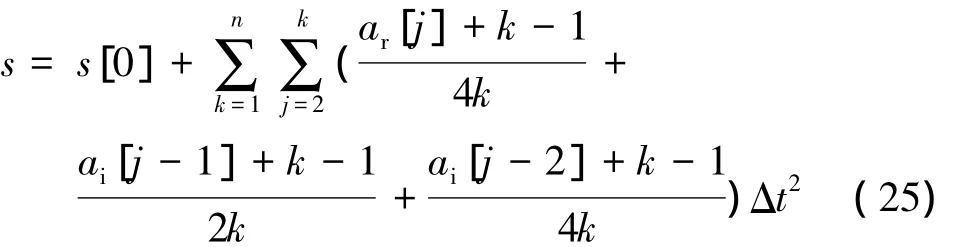
在进行标准试验时,已知s[0]和每个时刻n的加速度数值a[n],根据式(25)就可以计算出k值,随后将k值带入到位移控制算法中进行加速度修正。
3 系统硬件设计
此测量系统采取集成化设计,共分为电源模块、测量模块、存储模块3部分,各个模块之间的关系如图1所示。

图1 系统整体框图
测量模块采用MXC400xXC热对流式三轴加度传感器精确获得运动载体的加速度信号,测量值以数字量通过IIC接口输出。为增加获取的实验数据,在电路板上下两面的中心处分别安装一个加速度传感器,便于对比分析和数据验证。测量系统的处理器选用TMS320D28027芯片,此系列DSP芯片采用先进的哈佛结构,即存储线和指令线并行,在数字信号处理方面具有十分独特的优越性。其配有专门的数字信号处理算法指令,运算速度快,结果更加精确[9-10]。
供电模块使用3 V干电池供电即可满足要求。本系统为了充分减小体积,设计了一种高性能锂离子电池,其储存总电量 55 mA·h,额定电压为 3.7~4.2 V,经过接入电路板测试,在放电电流约为100 mA时,电压3.7 V以上工作时间约为50 s,满足相关供电需求。其尺寸和外形如图2所示。
图2 锂离子电池外形图与尺寸图
存储模块采用FM25V20A铁电存储器,它是一款集低功耗和高性能于一体的非易失存储器,在没有电源时不会丢失存储的数据,并且可以长时间地保留数据,随用随取。实验结束后将数据传输至电脑进行数据分析和处理。
存储模块用于线下的数据观测和分析处理,实际应用时存储模块可去掉,可由测量板上的DSP直接输出位移结果。整体测量系统如图3所示。

图3 位移测量系统
4 定距实验
4.1 实验装置
为了验证位移测量系统的综合性能和定距精度,设计了直线滑轨定距实验,实验装置如图4所示。轨道长4 m,等间距设置螺纹孔用于滑轨调平。滑块与轨道为滚珠接触,在垂直滑道方向卡紧滑块,减小二者之间摩擦的同时保证左右滑动时的稳定。

图4 直线滑轨定实距验台
4.2 实验方案
为了对试验数据进行详细分析以及对试验过程的数据进行监控,本实验利用存储测试技术进行直线滑轨定距实验,即采用存储测试技术存储滑块滑动过程中的有效数据,在线下对数据进行处理分析。存储测试技术指的是在测量系统中采用存储装置,此存储装置不会对被测对象产生影响或产生的影响比较小,不会影响原系统的正常运行,在运动过程中完成数据信息的实时快速采集与记录,试验结束后传输存储装置中的数据,利用计算机再现测试信息并分析处理。
将位移测量系统固定在滑块上,确保加速度传感器的X轴与前进方向平行。将滑块置于滑道一端,在另一端设置挡板,用人力手拉滑块分别进行2 m和4 m的定距滑动,滑块撞击挡板后等待单次18 s采集周期结束,后取下存储板读取数据,通过线下对数据进行积分处理来利用加速度实现对位移的解算,观察实际测量精度。
4.3 实验过程
首先利用激光笔调平直线滑轨。然后利用清零程序将存储板数据全部清0,连接好测量系统,按照方案设计固定至滑块上。将滑块滑动到位之后,打开电源开关,看到LED指示灯亮起,说明电路开始正常工作,滑块静止7 s左右后开始拉动。拉动时注意用力要猛,防止滑块出现后退或者起步困难等现象。开始滑动后尽量以平滑的速度使滑块向前运动,直至撞到滑道末端的挡板,如图5所示。此时并不马上关闭电源,等测量LED指示灯熄灭,代表单次测量周期结束后再切断电路,取下存储板并读取数据。然后在计算机上对数据进行线下处理。以此过程分别进行3次2 m和4 m滑动实验。

图5 滑块撞击挡板
4.4 实验结果与分析
2 m与4 m直线定距测试分别进行3组,部分原始数据如表1所示,测试结果如表2所示。由于篇幅限制只分别展示其中一次的加速度-时间图线以及部分加速度数据,如图6所示,其中图6(a)、图6(c)为存储器内全部数据绘制的图线,图6(b)、图6(d)为将运动过程截取之后的数据图线。

图6 部分加速度-时间图线
从图6可以看出,前700个数据点对应静止的7 s,此时加速度传感器的数据在0上下浮动。开始运动后,观察可知轴的负向为滑块的前进方向,首先经历一个迅速的加速过程,图6(b)、图6(d)出现一个向下的尖峰;之后滑块进入较为平稳滑动过程,所以此时滑块加速度逐渐变小;等到滑块撞击挡板时出现一个正值的高冲击过载,此冲击值远远大于加速度传感器的量程,故传感器为满量程输出。之后在稍微的扰动过后加速度传感器输出马上趋于稳定。实际撞击后滑块有可能出现小幅的后退,冲击后的扰动即对应滑块的轻微后退。稳定后的输出值仍在0上下浮动,前后状态大致不变,系统运行稳定。

表1 传感器原始数据
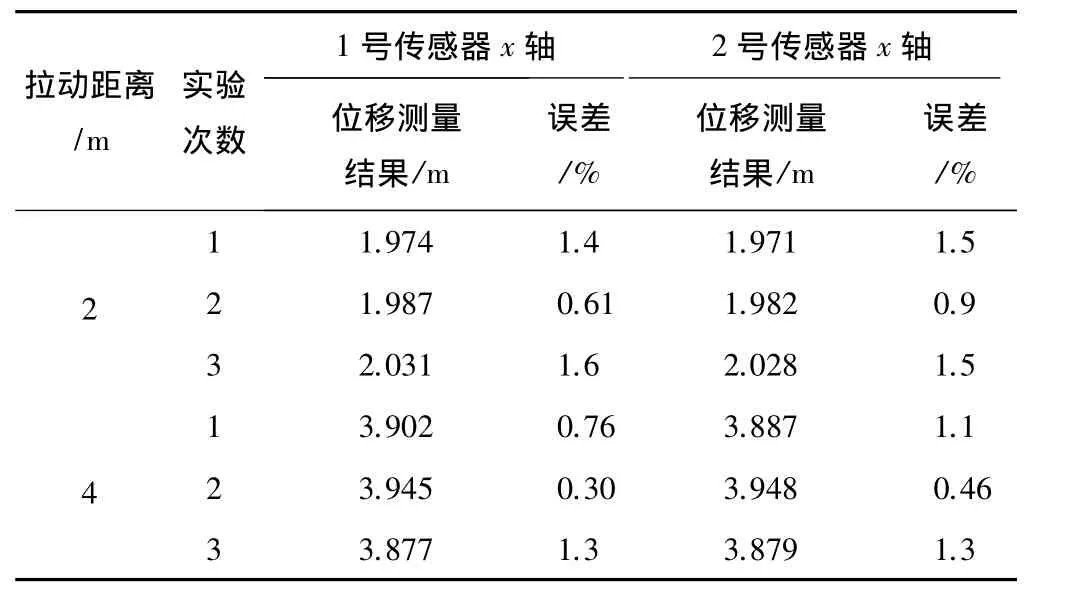
表2 位移测量结果
4.5 数据分析
从实验结果来看,2 m和4 m均有较为精确的位移测量结果,最大误差为1.6%,最小误差可达0.6%。经过分析,造成误差不同的原因有:
(1)受到滑动距离的限制,误差难以进一步控制;
(2)滑动过程由人力控制,拉动过程力的输出方向、大小难以控制。对比可以发现较为准确的实验图线较为平滑,而误差较大的实验则加速度数据很不稳定,这对积分的结果有一定影响;
(3)滑道不可能保持绝对水平,中间存在弯曲和变形,影响位移测量结果。
5 结论
经过直线滑轨实验台测试可以看到,本位移测量系统不仅体积小、可靠性强,并且精度高,能够准确反映出运动载体的直线运动状态,在引信定距、车载导航、飞行器惯导、智能电子产品等领域具有十分广阔的应用前景。

