基于最优变现时间的存货质押融资质押率研究

邓逸男 （昆明理工大学 管理与经济学院，云南 昆明 650093）

0 引言

随着我国供应链金融业务的不断发展，存货质押业务在中小企业融资中也扮演着越来越重要的角色，存货质押融资业务是指资金提供方根据借款方所提供的质物，向借款方出借资金。并由第三方的物流企业作为中介方，对质物进行合法保管。在我国，由于市场风险及自身缺乏不动产等原因，中小企业往往难以获得银行贷款，以中国建设银行的“小微企业信用贷”为例：最高贷款金额不超过300万元，且需达到银行规定的信用评级。各大商业银行对中小企业申请贷款苛刻的要求。使得中小企业虽然占我国企业总数的99%，并且每年为我国贡献63%的GDP，却只占有不足20%的金融资源[1]。西南财经大学发布的《中国中小企业发展报告》显示，在全国约5 800万中小企业中，仅25.8%的中小企业有正规借贷渠道，且只有46%的企业获得了银行贷款[2]。存货质押融资业务的出现，为中小企业走出这一困境提供了新的路径。但是，该业务各参与方对供应链系统风险、信用风险等各项风险的担忧，仍然制约着存货质押融资业务的发展。质押率是存货质押合约中的关键风险控制指标，同时还体现着质物的担保能力。因此，质押率成为了存货质押融资业务各方共同关注的焦点。质押率是指贷款本金与标准仓单市值的比率，其设定的核心在于预测质物长期价格风险。商业银行通常规定“以货物或者货权质押的，为借款人提供融资的比例最高不得超过质物价值的70%”[3]。但这种一刀切的设定往往不够精确，因而，探索如何合理的设定质押率具有重要的意义。

1 质押率相关变量模型构建

1.1 最优变现时间

为了根据质押期间风险的变化动态地设定质押率，商业银行应选择合适的风险窗口T来度量实时、动态的流动性风险。风险窗口T一般被视为变现时间。在现有文献中，变现模型一般都来自于股票、证券市场，然而考虑到流动性较弱的农产品市场与金融市场在交易模式等方面的不同，因此本文假设在连续时间框架下，给出作为质押物的存货在现货市场上进行交易的最优变现策略。

假设市场价格运动缺乏趋势性，按照Smith&McCardle[4]理论，认为市场价格服从几何布朗运动，但几何布朗运动不便于数学运算，因此，本文用算术布朗运动代替几何布朗运动，即：ds=σdWt，其中Wt为标准维纳过程。令x0=X为初始待变现存货量，xT=0为期末存货量，质押存货的清算速度为vt=-dx/dt。Almgren和Chriss认为价格变动受漂移率、波动率和市场冲击三种因素的共同影响。根据Hlothausen等[5]的观点，本文将市场冲击分为永久市场冲击和瞬时市场冲击。假定市场冲击与变现速度之间为线性关系，因此，永久市场冲击为g vt［］=γvt,γ＞0，γ为永久冲击系数，瞬时市场冲击为h （vt）=ηvt，η＞0，η为瞬时冲击系数。

在以上假定下，市场交易价格为：

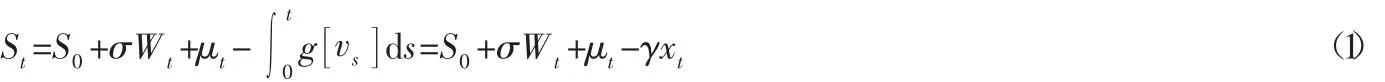
其中：σ为质押物价格的波动率，μ为质押物价格的漂移率。由于瞬时冲击效应的存在，真实的交易价格为：

采用执行损失思想描述变现成本，则银行变现成本为：

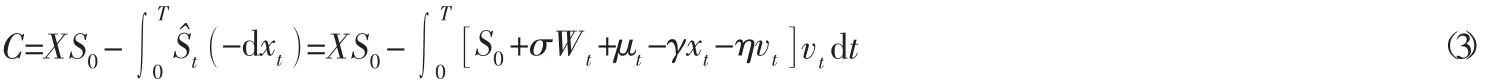
根据王春峰等[6]在股票市场中所使用的清算策略｛xt｝=x0,x1,…,xn，本文将VaRp（x）定义为：在变现期间内，变现策略在p置信水平下可能造成的最大交易成本，因此，有：

其中：Zp为标准正态分布的p分位数，表明在清算策略｛xt｝下，交易成本不超过VaRP（x）的概率为p。以实现银行变现成本最小化为最优变现目标，因此，最优清算策略等价于式（4）最小值时的清算策略，即：

Bertsimas和Lo[7]认为最优变现策略是指假设市场冲击函数是线性的，股票价格服从随机游走过程时，以固定的速度卖出股票的策略。因此，假定以恒定的速率卖质押物，则：

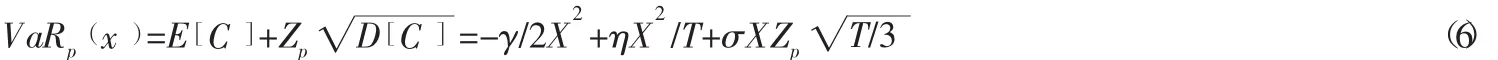
在连续时间框架下,最优变现时间可以表示为:

即连续时间框架下最优变现时间是由待变现存货量X，瞬时冲击系数η，质押物价格的波动率σ所决定的函数。

1.2 AR （1）-GARCH （1,1）-GED 模型

假设Pt是质押物在t日的市场价格，Pt-1是质押物在t-1日的市场价格，日收益率为：

GARCH模型可以用于解决时间序列的波动性问题，引入了以下GARCH（1,1）过程：

其中：μt为t日收益率的条件均值，εt≡σtzt为随机扰动项，λ是一阶自相关系数，σt为t日的条件波动率，为t日的波动率的条件方差。本文假定由AR（1）过程描述自相关，α0为常数项，α1为ARCH项的参数估计值，β1为GARCH项的参数估计值，令φ=α1+β1，收益率的无条件方差为：σ∞=α0/1-φ。为确保条件方差对应的所有zt过程保持为正，且GARCH模型平稳，需满足约束条件：（1） 参数限制为非负，（2） α1+β1＜1。

本文使用GED分布来刻画收益率序列的尖峰厚尾特征，假设zt服从GED分布，其概率密度函数如下：

1.3 质物VaR方法的建立及质押率的确定

现有的VaR文献在长期风险衡量方面提供的最著名方法是平方根规则，即然而遗憾的是，这一规则并不足够可靠，它可能造成对VaR一定程度的高估（参见，Blake[8]等人的文献）。因此，为了解决这个问题，本文引用了Dowd[9]对时间平方根法则的修正，即：

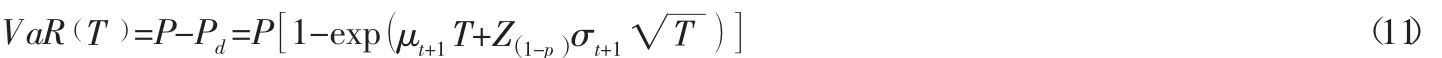
其中：P是质押物的当前价值，Zp是与我们选择的置信水平相关的标准正态变量。

质押率是贷款本金与质物当前市场价值的比率，而贷款本金V等于质物初始价值减去可能的损失，即则质押率可以表示为：

2 实证分析

本文数据来自西本新干线提供的上海热轧卷板Q235B/SS400的价格波动数据，选取的时间段为2015年6月1日至2018年6月1日，共749个样本点。假定对热轧卷板进行模拟质押，质押期间从2018年9月1日开始，质押期设为6个月，选取置信度为95%，Zp=1.65。引用Bikker[10]对瞬时冲击和永久冲击的定义，得η=0.0007298。

2.1 收益率序列波动特征和正态检验结果考察

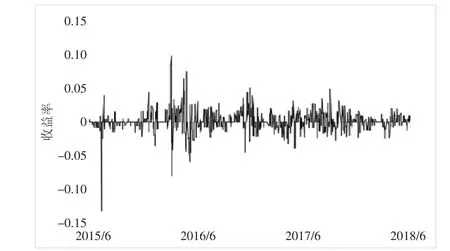
图1 热轧卷板收益率线性图

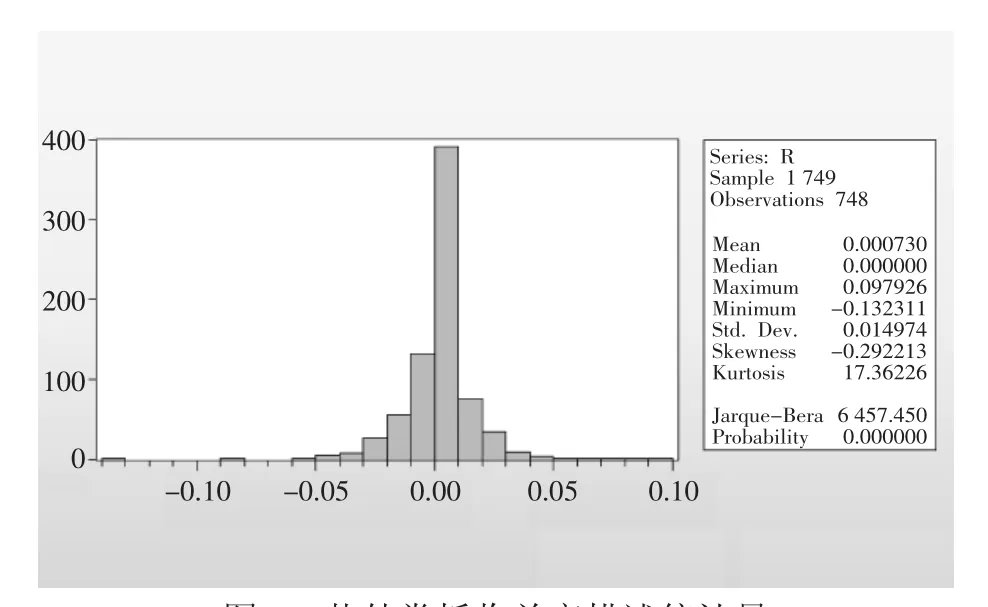
图2 热轧卷板收益率描述统计量

图1可得，热轧卷板的收益序列的波动具有明显的集聚效应。图2可得，收益率序列偏度为-0.29，小于0，说明序列分布左侧尾部比右侧长。峰度为17.38，远大于正态分布的峰度3。说明收益率序列具有尖峰厚尾的特点。J-B统计量为6 457.45，P值为0，说明拒绝“收益率服从正态分布”的假设。

2.2 收益率序列平稳性、自相关及ARCH-LM检验考察

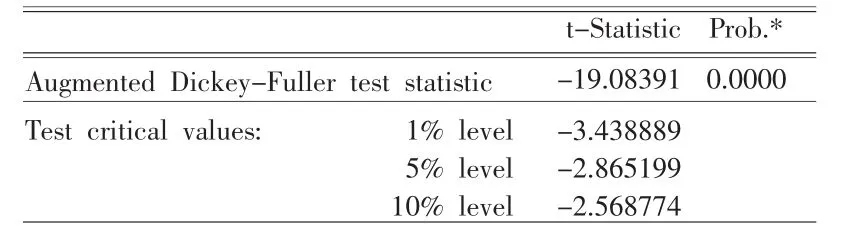
图3 收益率序列ADF单位根检验

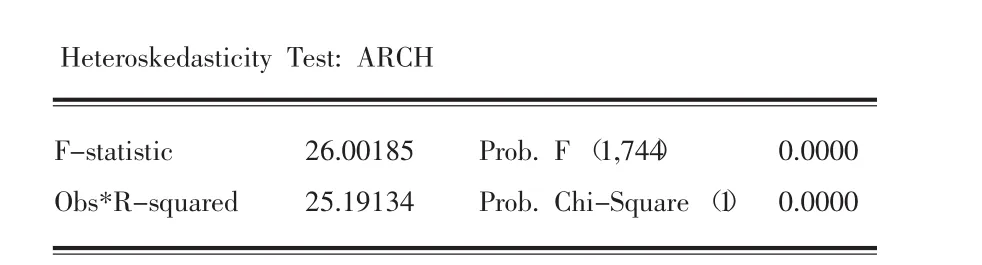
图4 收益率序列残差项ARCH效应检验

为了考察收益率序列平稳性，本文运用了ADF单位根检验法，由图3可得，收益率序列的t统计量为-19.08，对应P值为0，且小于检验水平1%、5%、10%的t统计量检验值，说明收益率序列是平稳的。对收益率进行了滞后20阶自相关性检验，结果得出一阶自相关和偏自相关系数都超过了95%的置信区间，且Q统计量对应的概率均为0，说明存在显著的自相关。同时，根据图4中ARCH-LM检验的结果，统计量F为26.00，T·R2统计量为25.19，对应概率值均为0，说明拒绝“收益率序列残差项不存在ARCH效应”的假设。

2.3 质押率测算结果

表1 AR（1）-GARCH（1,1）-GED模型参数估计结果

由表1，模型参数估计结果可得，GED分布中的参数y=1.17，小于2，根据前文所述，再一次验证了收益率序列具有尖峰厚尾特征；常数项c接近于0，且对应z统计量概率值也接近为0，因此可以忽略；其他各估计的z统计量概论值均为0，即系数显著，根据赤池信息准则，模型数据拟合较好，残差序列不存在自回归条件异方差效应，进而得出在GED分布下GARCH（1,1）模型是合理的。因此模型对应的条件均值方程和条件方差方程可以表示为：

α1＋β1=0.985＜1,α0＞0,α1＞0,β＞0满足前文中GARCH（1,1） 模型平稳所需满足的两个约束条件，无条件方差可表示为：σ∞=1.13E-04。

据此，在假定持有不同质押存货头寸条件下，热轧卷板最优变现时间及质押率测算结果如表2所示。

表2 不同存货头寸条件下热轧卷板质押率设定

2.4 质押率合理性检验

为了检验本文模型设定的质押率精度，需要进行失败率检验，即统计VaR对质物实际损失的覆盖程度。本文采用被广泛运用的Kupiec[11]的失效率检验方法。分别对传统时间平方根法则设定的质押率和本文采用的AR（1）-GARCH（1,1）-GED模型设定的质押率进行合理性检验，结果如表3所示：

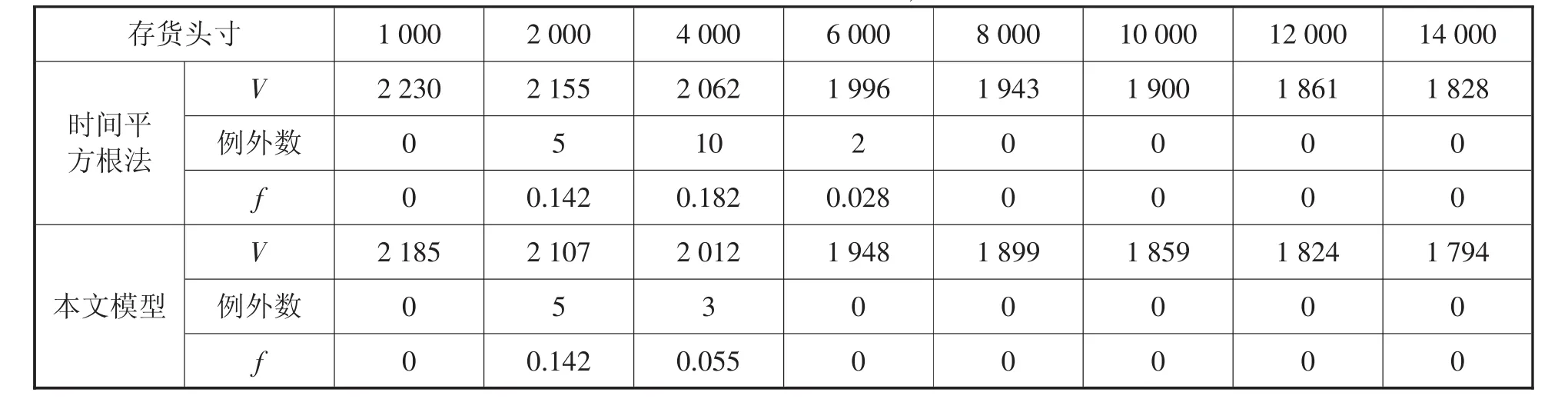
表3 使用时间平方根法则设定与AR（1）-GARCH（1,1）-GED模型的质押率合理性检验

观测表3中的V、例外数、f等变量，使用传统时间平方根法则在大部分情况下，能够正确预测长期风险值，但是在存货头寸2 000、4 000与6 000处，预测价格与实际价格分别出现了5、10和2次的例外数，特别在2 000、4 000处失效率超出了95%置信水平所接受的例外情况，与之不同的是，使用本文模型，虽在2 000、4 000处出现了例外数，但失效率明显低于时间平方根法则。因此，使用本文中AR（1）-GARCH（1,1）-GED模型对长期价格风险预测的准确度要优于时间平方根法则。但不容忽视的是检验结果在2 000存货头寸处出现了0.142的例外，超过95%置信水平所接受的例外情况，这也说明了仅采用本文模型进行质押率设定并不能达到完全的精确。

3 结论

尽管我国存货质押融资业务发展潜力巨大，但供应链系统风险、信用风险等各项风险的存在仍然制约着它的发展。此外，在存货质押合约中，如何正确预测质物的市场价值也是一个关键的风险点。而质押率是存货质押合约中的关键风险控制指标，同时还是质物担保能力的重要体现。因此质押率的合理设定具有重要的意义。综上所述，本文的主要贡献有两点：一是将股票市场的最优变现策略引入存货质押率定价模型，得出基于变现时间的VaR模型；二是AR（1）-GARCH（1,1）-GED模型与RiskMetrics模型相比，对长期La-VaR值的预测具有更高的精确度，能够为中小企业质押融资提供一个较为合理的质押率模型。