基于天气对地铁的短时客流预测

金 聪，周健勇 （上海理工大学 管理学院，上海 200093）

城市轨道交通因为便捷、环保、经济等特征逐渐成为人们主要的日常出行方式。国家大力建设轨道交通来满足人民日益增长的出行需求，而有关部门也迫切需要掌握不同时段及各种影响条件下客流变化的规律，方便后续针对性的开展关于客流预测以及拓流等工作。相关研究表明，当出现不利天气情况，如：下雨、刮风或者雾霾天气时，地铁客流量会呈现波动状态，对地铁当天的运营情况造成一定的影响。除了天气，其他一些如节假日等客观因素也会一定程度上影响到当天的客流情况。因此通过分析掌握好在不利天气因素以及其他客观因素条件下客流变化的规律，不仅可以增加一定的经济效益，也能一定程度上为轨道交通更好的运营和开发建设提供战略性规划的指导意见。

1 研究方法

国内外针对城市轨道交通客流主要从客流量受气象温度或者是各类恶劣天气因素影响分析、轨道客流影响因素关联性分析、城市轨道交通客流预测等方面着手研究。

关于城市轨道交通的客流预测，王飞[1]通过对包含出行生成、出行分布、交通方式分担以及交通分配方式的预测来生成客流预测的模型。卢志义[2]采用自回归滑动平均时间序列（ARMA）模型对天津1号线客流量进行预测，提高了预测的精度。

杜恒[3]通过基于天气的随机场客流预测模型对乘客出行目的进行预测并拟合路网实时的客流分布，提高了客流预测的精度。李军龙[4]基于多元回归线性模型对雨雪天气下的交通出行需求以及基于SEM-MNLN模型生成居民在雨雪天气的出行方式进行分析和研究。

王静[5]通过对轨道交通客流影响因素分析，得出客流在不同区域不同时段显示出的差异性。马晓毅[6]则得出高效运营、土地开发程度、城市发展成熟度等6个因素对客流大小有明显的影响。

本文数据包括宁波地铁3条线的客流数据，网络获取的天气数据以及各站点周边业态分布的数据。首先通过K-means聚类对宁波现有的站点进行分类，针对不同类型站点分别做预测。其次通过大量阅读关于天气因素引起客流量变化的论文筛选出影响客流变化的指标。以筛选好的指标用于预测中，通过多元线性回归模型来预测客流，并在初步预测的基础上对模型进行优化，继而提升预测的精度。同时引入KNN预测客流的方式，比较两种方式的预测结果。

2 站点类型判别

各类因素对地铁站点客流的影响程度也因为站点的类型不同而变化，比如当出现大雨或低温天气时交通枢纽类型的站点客流并未受到很大程度的影响，而同等条件下对应的居民生活区的站点客流会受到很大程度的影响。为了研究针对不同类型的站点在天气及其他影响因素条件下的客流预测，应先对站点进行分类。

本文选取站点工作日日均客流、进出站客流峰度、进出站客流偏度、客流高峰小时系数、客流时段分布均衡系数、客流ABBA日均（7月到8月）、周边办公楼数量、周边居民区数量作为站点类型判别的指标，如表1所示：

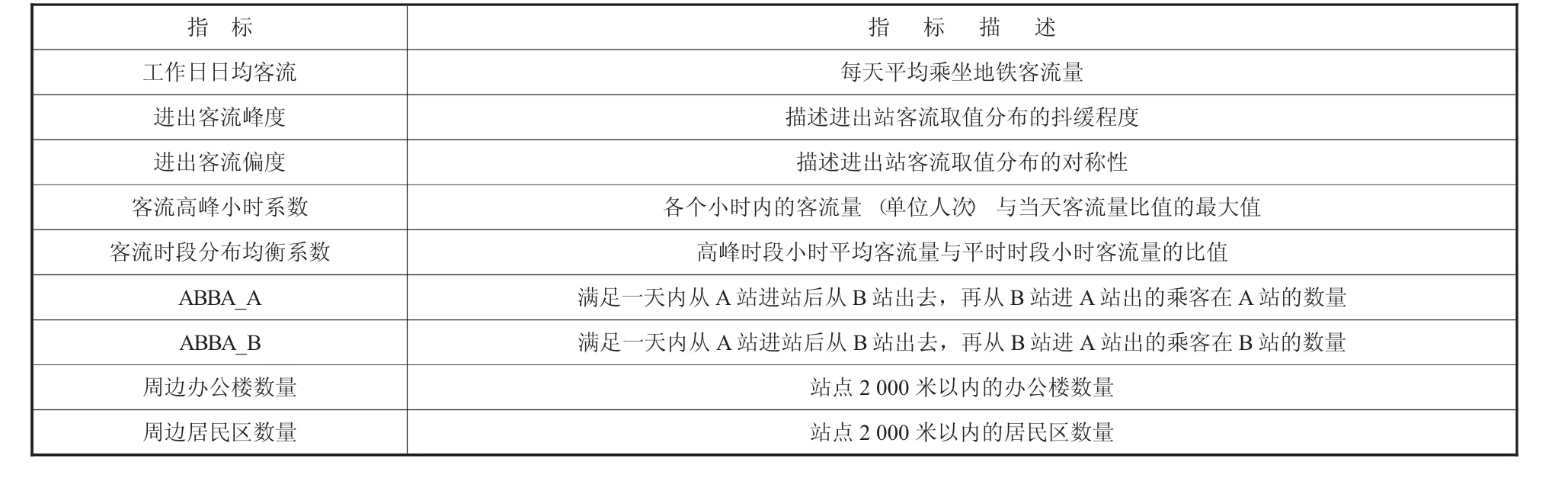
表1

为了降低指标数据之间因为数值大小、数值类型以及对应区间的差异可能会对聚类的结果造成影响，因此对数据做标准化的处理。在标准化处理方面采取归一化处理的方法，即将各项数据处于同一数据区间内，方便对其统一进行评价分析。原始数据经过数据标准化处理后，各指标处于同一数量级，适合进行综合对比评价。由于采取的指标数据相对来说较为集中，采用离差标准化，将数据的大小统一在0到1之间。函数如下

通过标准化后的部分数据如表2：（注：由于进站客流与出站客流之间峰度以及偏度相关性很强，因此选取进站客流的峰度及偏度）

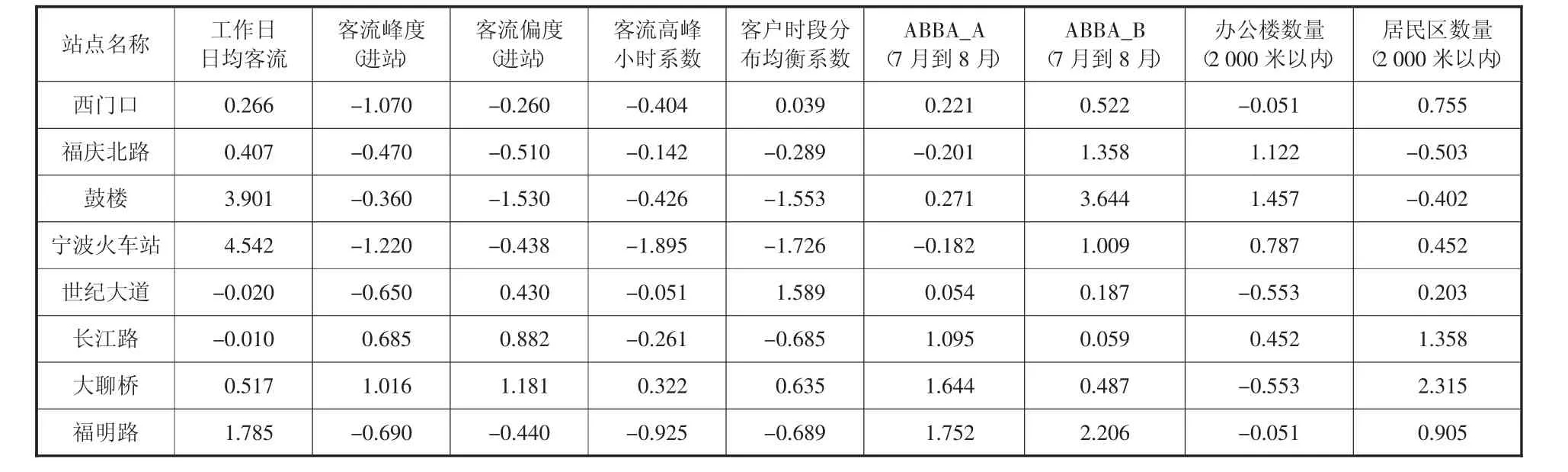
表2 标准化后的站点指标数据

2.1 K-means聚类。由于本文采取的站点聚类数据样本较少，为了优化少量样本分类不合理的情况，通过采用K-means聚类的方式基于已知的少数聚类样本对树剪枝并多次迭代修正聚类的样本，一定程度上降低了聚类的时间复杂度。

K-means聚类的本质是不断迭代，不断求解。首先随机定义K个聚类中心对象，在计算这些定义好的对象与不同子聚类中心的距离。通过距离的计算，将K个对象包括在最近的聚类中心里。此时就可以将对象与聚类中心看成是一个聚类。每当聚类样本增加时，聚类的中心会随着现有的对象而更迭。

2.2 聚类结果。在聚类之前，由于宁波栎社机场、宁波火车站、宁波客运中心站这类明显表现为交通枢纽类型的站点且不同天气对其影响因素不大，从聚类的站点中抽出，以便聚类的效果更加明显。如图1所示，通过K-means聚类的结果表明：将宁波的地铁站点分为4个类型。第一类是以五乡、世纪大道这类周边居民区分布特别多、又分布很多混合偏居住类型其他业态的站点；第二类是泽民、高桥这类居住型的站点；第三类是以鼓楼、城隍庙为主的商业商务混合类型的站点；第四类是以鄞州区政府、体育馆、儿童乐园这类偏职能类型的站点。下文以这些具有明显特征的站点作为研究对象分别对其进行回归模型的预测。

3 预测指标选取

研究表明，随着季节性的气候变化，如当温度表现为夏天的炎热或者冬天的寒冷时，人们的出行需求会改变，出行方式也会受到影响而发生改变。一定程度上影响了轨道交通客流量。相关论文基于出行目的的分析建立天气影响出行的模型，并得出降雨、雾霾天气以及刮风天气会影响客流量。

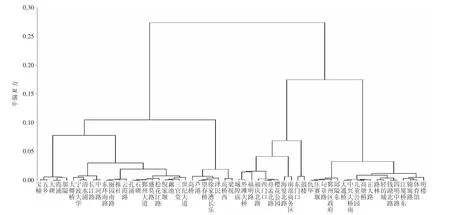
图1 站点聚类图

综上本文选取的预测地铁客流的指标为：天气因素（8～10月），包括降雨量情况、能见度、温度、风速、历史进站客流数据。

其中降雨量的单位为毫米，温度指标采用的是平均温度，历史客流数据主要采取宁波8、9、10月份的进站客流数据。在计算客流指标时采取以下处理：首先定义站点全日客流的平滑值，即取一个正常天气的日期，并找出与它相近的前后3个正常天气的日期，将这7个日期的平均客流作为当日客流的平滑值。计算公式如下：

其中：His表示客流平滑值，rz表示日期i与它前后3个正常天气日期的客流情况。

再定义降雨客流的基准值，即确定一个降雨的天气，并以这个星期的这天为中心，向前后分别找寻3个非降雨天气的同一星期内的日期，取这些日期的客流平均值作为降雨客流的基准值。计算公式如下：

其中：Hie表示降雨客流的基准值，rz表示日期i前后3个没有降雨天气的客流平滑值，单位为人/天。

由于宁波8、9、10月份的降雨天气样本较小，为了精确定义站点客流的波动率，因此本文以宁波1到7月份的客流样本来计算客流的波动率。计算公式如下：

其中：Rg表示客流的波动率，Hg为当天下雨时的实际客流，单位为人/天。

为了研究天气指标与客流量之间是否具有很强的线性关系，先对其做皮尔森相关性系数研究，它是用来表述两个数据是否在同一条线上。一般判定结果以相关系数所处的取值范围来判断，当系数处于0.8与1之间相关性极强，处于0.6与0.8之间相关性强，处于0.4与0.6之间相关性中等，处于0.2与0.4之间相关性弱，处于0到0.2之间无相关性。皮尔森回归值如表3所示。

如表3，从结果可以表明各类指标间的范围大部分都处在0到0.2之间，说明各类指标间的相关性不强，可以用于下文的回归预测。

表3 皮尔森回归值

4 多元线性回归预测客流

4.1 多元线性回归。在研究天气对客流影响时，考虑到选取的几个影响指标都会对地铁的客流量变化产生影响，而且无法说明哪些因素对客流的影响较大，哪些影响可以忽略。因此本文采取多元线性回归分析。

假设因变量即客流量的大小为y，自变量即影响的因素分别为x1,x2,x3,…,xk，并且自变量与因变量之间为线性关系时，则多元线性回归模型为：

其中：b0表示常系数，b1,b2,…,bk表示回归的系数。回归系数b1表示当其他的自变量固定时，每当x1增加或者减少时对应的y的变化，即x1对y的偏回归系数。同理可得b2,b3,…,bk。

使用最小二乘法进行参数估计，公式如下：

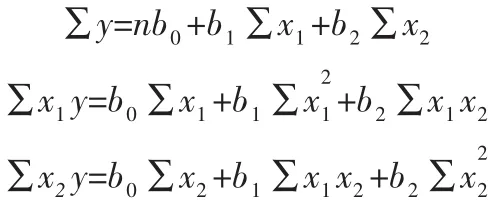
表4至表7为多元预测回归完后，真实客流数据与预测值的情况。

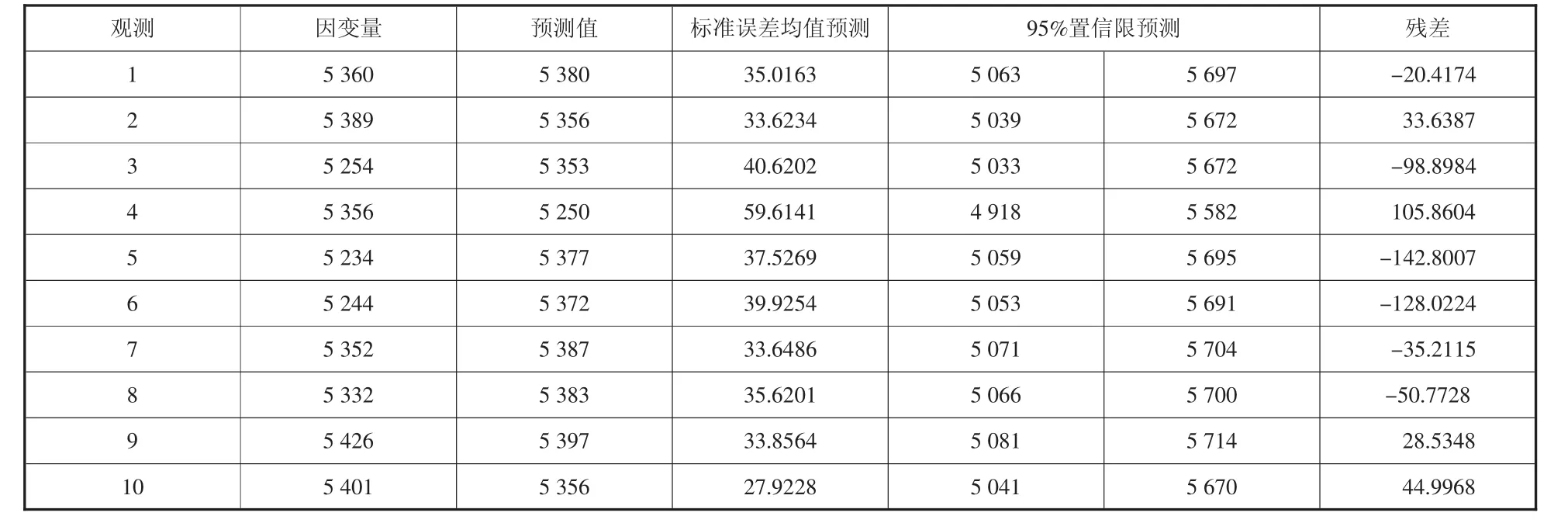
表4 类型1站点客流预测

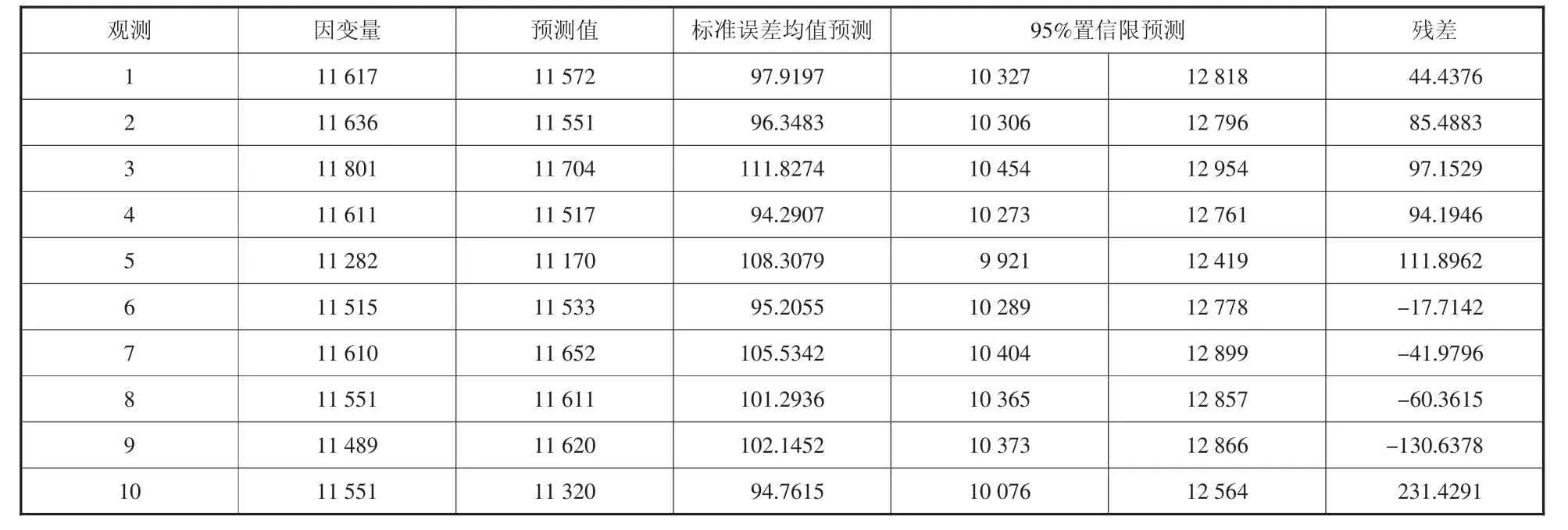
表5 类型2站点客流预测

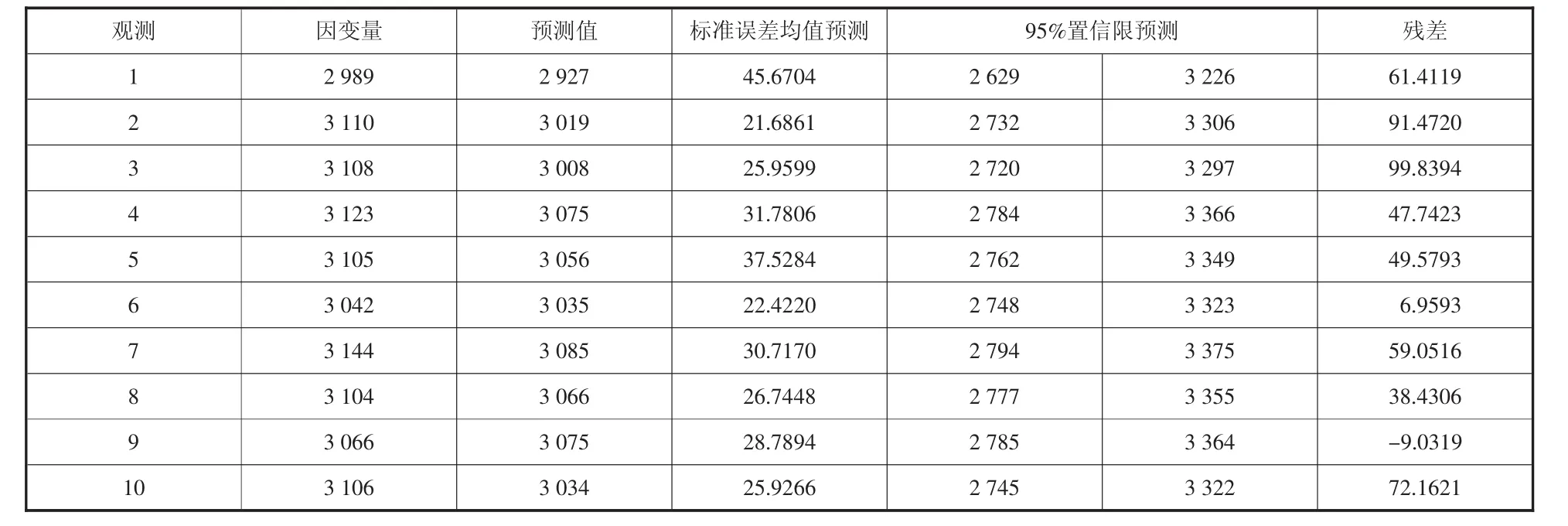
表6 类型3站点客流预测

4.2 参数检验。一般计算得到最小二乘法的估值后，会通过检验回归值与实际值的拟合程度来评价回归模型的效果。通过估计F检验，将所有影响因素即自变量作为整体来检验其与y之间的相关程度，评价其回归效果。F检验公式如下：F

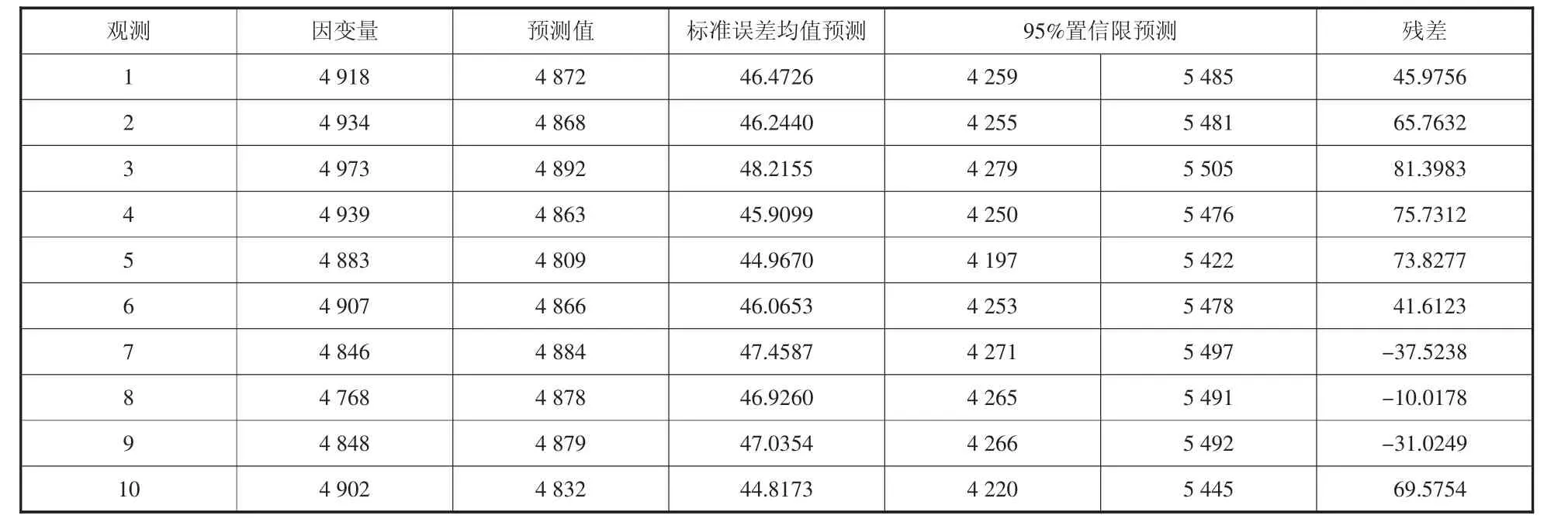
表7 类型4站点客流预测

回归模型的稳定性容易受到自变量与因变量以及自变量之间线性关系的影响，最后导致回归系数无法确定。在建模过程中会碰到多重共线的情况，为了避免方程发生多重共线，一般会通过计算变量之间的可决系数或者计算自变量间的相关系数特征值。因此为了检验各项影响指标是否对地铁客流有影响以及影响的程度，通过多重线性判别检验将结果不显著的解释变量去除，并重新建立回归模型，从而提升预测的精度。

以站点1为例，由参数估计结果（如表8所示）表明：能见度、温度、风速对应的Pr值都超过了0.005，且R方值远低于0.9，即在类型1站点的能见度、风速、温度对其影响不是很大。因此将这些影响指标去除再做一次回归预测来观察结果。

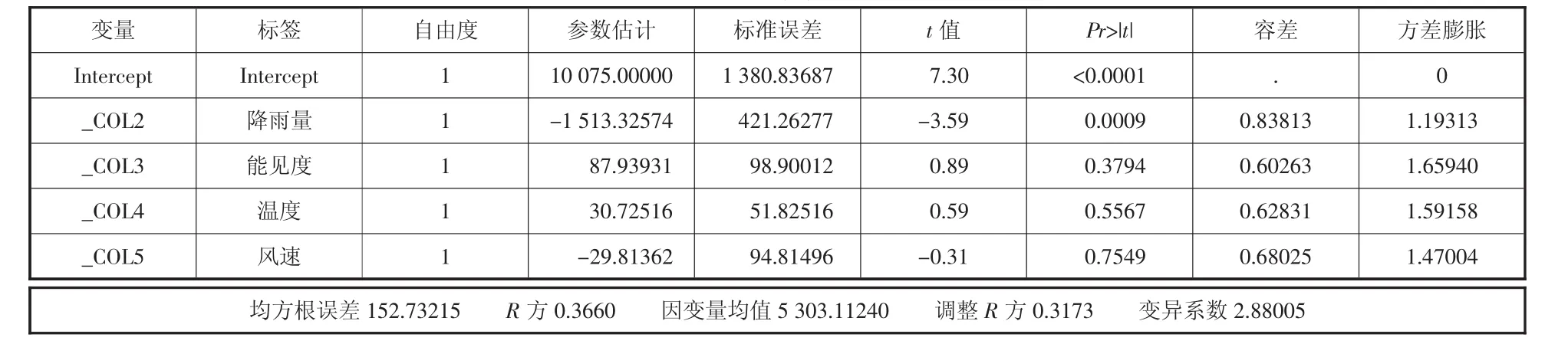
表8 参数估计表

表9即为去除相关影响指标后的参数估计。通过筛选影响指标再做预测模型后，从结果中可以观测出对应的Pr值以及R方数值都在正常范围内，初步完成了模型的优化。

表9 参数估计表

4.3 KNN模型预测。在影响因素模型中同时采取K近邻算法。KNN因为预测结果与实际的误差率小且对异常的数值不敏感而被用于预测客流方面，这里的预测模型采用的是加权平均算法。

（1）首先定义影响客流预测的因素。用y1表示预测时段前n个时段的客流量状态，用y2表示受天气因素影响的客流量状态。

（2）测量距离，即y1与y2的加权欧式距离。公式如下：

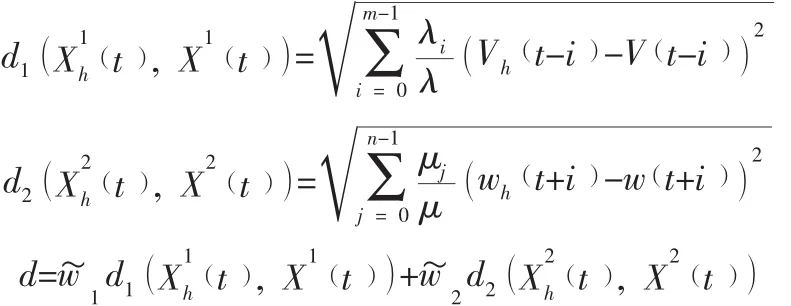
（3）加权平均预测给予每个近邻不同的权重，假设与测量距离越小的近邻对预测的贡献度越大。权重一般取假设与测量之间的倒数，各近邻的权重大小取决于其对预测值的贡献的大小，各近邻权重为：

式中：di为第i个近邻与状态向量之间的欧式距离；d为各加权距离倒数之和。根据上述的近邻值和权重，可预测下一时段的客流量为：

KNN预测的部分结果如表10：

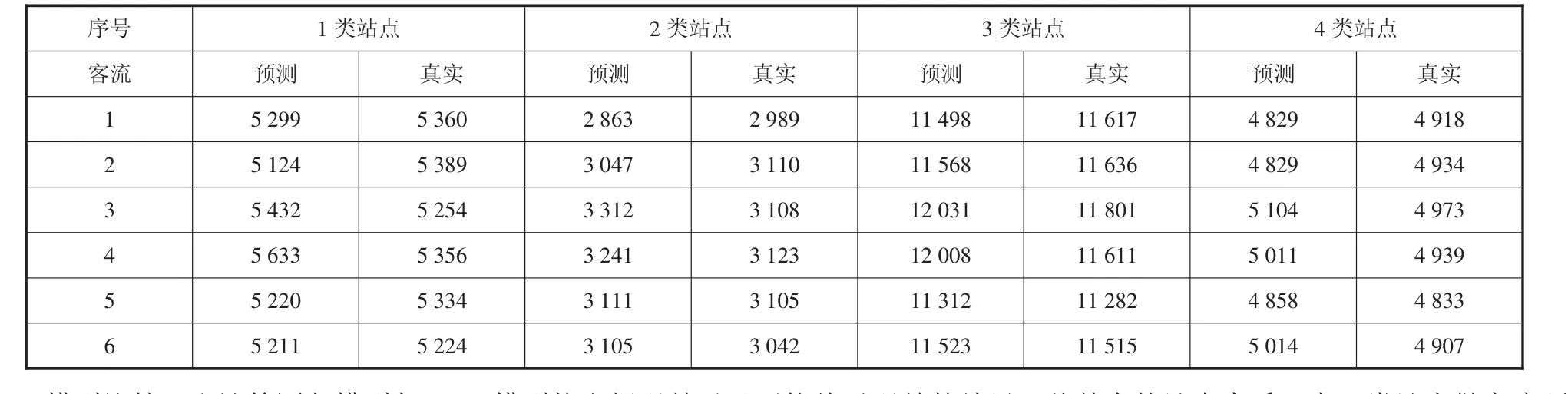
表10KNN预测表

4.4 模型比较。由计算回归模型与KNN模型均方根误差以及平均绝对误差的结果，从单个的站点来看：在1类站点做客流预测两种算法的结果相近，但是在2、3、4类站点预测的结果是多元线性的预测误差相对小一些。从总体来看，多元回归平均MAE为131.51，平均RMSE为224.87；KNN预测平均MAE为165.66，平均RMSE为281.71，即在客流预测上多元回归的效果更好一些。

表11

5 总结

本文之所以采取短时客流预测：一是由于历史客流量的采集比较困难，采集到的数据量较小；二是从长期发展角度去做客流预测需要考虑的因素太多，不可控因素比如城市的建设规划、城市的经济发展状况、人口的出行需求特征等都是处在不断的变化状态中，对长期预测中的预测精度会造成影响。

本文采取相应算法构建预测模型以及在站点分类型时采用聚类算法将地铁站点进行分类，收集地铁客流数据、天气情况、站点周边业态分布情况等数据，划分出不同的站点类型，并对各类型不同影响因素进行分析，短时预测当天的客流情况。在站点分类阶段，本文通过K-means聚类将宁波的站点分成4类：混合偏居住类型，居住类型，商务商业混合类型以及偏职能区类型的站点，并在此基础上分别基于多元线性回归模型去预测客流。实际的结果都置于预测的置信区间内，表明基于天气因素通过多元线性回归算法能预测短时客流。

对于地铁短时客流预测是一个不断探索的过程，随着技术的不断创新，会有更多契合的算法、更适合研究的指标加入客流预测的过程中。