软基深挖引起既有桥梁偏位研究现状分析

韩海宏

摘  要：经济的大力发展需要以加大对公路、桥梁、港口等基础设施的建设，来满足日益增长的对交通的需求。基础设施的建设，往往伴随着基坑深挖，尤其在我国长江中下游地区，地质情况以软土居多，软土地基深挖使基础设施建设变得更加复杂。

关键词：软土地基  深层开挖  既有桥梁  现状分析

中图分类号：U441.2                           文献标识码：A                    文章编号：1674-098X（2020）12（c）-0020-04

Abstract： The vigorous development of economy needs to increase the construction of infrastructure such as roads， bridges and ports to meet the growing demand for transportation. The construction of infrastructure is often accompanied by deep excavation of foundation pit. Especially in the middle and lower reaches of Yangtze River in China， the geological situation is mostly in soft soil， which makes the infrastructure construction more complicated.

Key Words： Soft foundation; Deep excavation; Existing bridges; Status analysis

软基深挖引起既有桥梁偏位，是由土体滑移引起桥梁桩基偏位造成的，属于被动桩的研究范畴。虽然，国内外学者对整个桥梁的偏位研究较少，但对被动桩的研究已硕果累累。“被动桩”的概念最早是由DeBeer提出来的，是指为阻挡桩周土体位移而被动承受土压力的桩。

1  被动桩实验研究

在1948年，由Franx和Boonsrta最早报道了既有桥梁在土体产生滑移导致桩体偏位并造成破坏的观测资料，引起了众多学者的广泛关注。随后，Heyman（1965），DeBeer and Wallay（1972）等分别对被动桩进行了现场试验研究。研究表明：软土滑移将对既有桩体产生很大的侧向力，甚至使既有桩基发生断裂。在国内，一些科研院也先后对堆载作用下既有桩基的位移进行了监测，通过现场试验研究，取得了一定的成果。

日本学者Tomio Ito，et al（1982），以室内模型试验，研究了不同桩径和桩距时，土体的滑移对被动桩的偏移及受力产生的影响。该项试验实测结果，与其理论结果相吻合，验证了被动桩在土体作用下的塑性变形。我国铁道部第二勘测设计院（1986） 、南京水利科学研究院（1990、1992）等曾通过室内模型试验研究了抗滑桩在不同布置情况下，其桩体受到压力的分布情况，为抗滑桩的设计提出了有价值的结论：

（1）土体滑移作用于桩体的侧压力，基本以三角形的形式分布，与土体的类别无关。试验还表明，侧压力合力重心作用于滑动面以上抗滑桩桩长的0.26～0.30位置处。

（2）土体的下滑力，一部分被抗滑桩传至滑动面以下的稳定地层，另一部分传至桩前土体。

（3）桩前土体抗力的合力重心位于滑动面以上0.45倍的桩长左右，且抗力图形与抛物线形接近。

总之，对被动桩问题早期研究及处理形成的经验方法，不需要考虑土体性质，通过桩顶水平位移实测值、堆载荷载大小、桩体柔度等参数关系，绘制桩顶位移、桩身最大弯矩-荷载-桩土相对柔度关系曲线，以经验公式，推求桩身最大弯矩、位移等变量（Stewart 1992），使用具有局限性。

2  被动桩分析、设计方法研究

被动桩工程问题的处理关键，就是要准确计算出桩体承受的侧向力，分析出桩体所处的受力状态、变形情况。对于建筑工程深基坑支护中的这类被动桩，由于桩侧临空较高，一般可以运用主动土压力、静止土压力及被动土压力公式加以计算。对于基坑开挖中的既有建筑物桩基，由于桩前土体以及边界约束的存在使受力计算变得复杂。目前，国内外对被动桩的分析、设计方法分为如下三类。

2.1 基于土压力的分析、设计方法

（1）TomioIto（1975）塑性变形理论法。

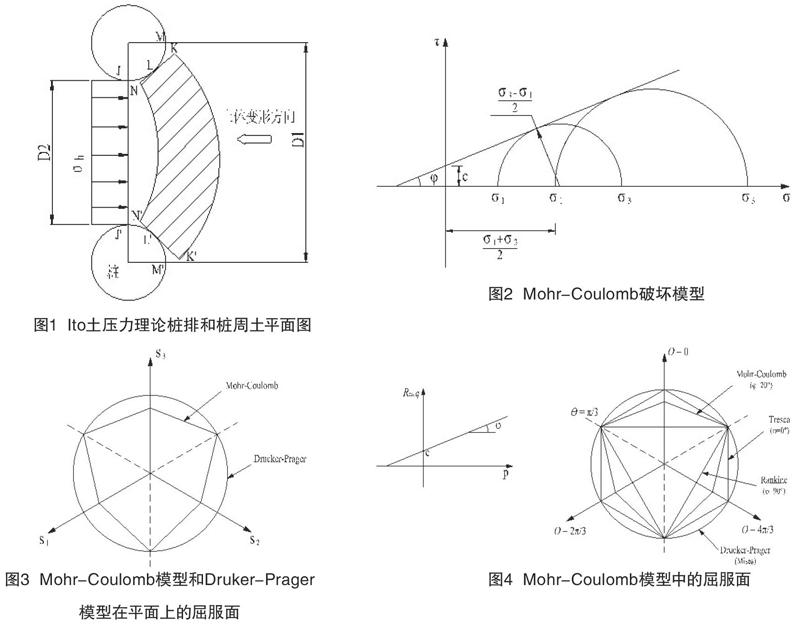
日本学者TomioIto，针对单排桩基，根据塑性变形理论，提出了移动土体产生的极限侧压力计算公式，如图1所示。

理论假设：

当土体发生变形时，将产生JNK和J′N′K′两个滑动面，NK和N′K′与X轴的交角等于π/4+φ/2;

JNKK′N′J′區域土层为塑性，服从Mohr-coulomb屈服准则;

土层在深度方向服从平面应变假定;

桩体假定为刚性;

假设在JJ′面上作用主动土压力;

以塑性区JNKK′N′J′为研究对象，在计算其应力的分量时，认为作用在JNK（J′N′K′）面上的剪应力忽略不计。

根据塑性区JNKK′N′J′力的平衡条件，认为作用于平面KK′和平面JJ′上的侧向力之差就是X轴方向上单位厚度土层作用在桩上的侧向力P（h）：

尽管该计算公式假设桩体为刚性，若弹性桩体在桩周土变形较小的情况下，仍可适用。

（2） 沈珠江散体极限平衡理论法。

在国内，沈珠江在考虑土体绕桩滑动的基础上，利用散体极限平衡理论推导出了绕流土压力计算公式。该公式的推导，作出如下假定：

土层无限广阔并沿水平向对垂直桩作相对运动;

桩表面绝对粗糙。

在上述假定基础上，以圆形桩为研究对象，推导出单位桩长上作用的绕流阻力：

式中，c为土体粘聚力，L为桩中心距，d为桩径，p为附加荷载。

TomioIto、沈珠江和A.C.CTPOFAHOB以不同的理论依据及假设，对桩周土进入塑性状态时桩体的受力，得出了不同的计算公式。研究表明，当φ=0时，沈珠江和A.C.CTPOFAHOB理论公式的计算结果很接近，而TomioIto理论公式在D2/D1大于0.3时的计算结果与沈珠江和A.C.CTP0FAHOB的结果较接近。

2.2 基于桩土变形理论的分析方法

（1）Poulos基于弹性理论的解答。

在Poulos对被动桩的分析中，将土体滑移中长度为H，宽度为B的桩等分为m段，则共有节点m+1个，认为每段长度H0，则通过建立有限差分格式，转化为m+1个代数方程，在考虑桩和桩周土位移相同的基础上，可推导出如下表达式：

式中，[D]为差分系数矩阵;[I]-1为土的位移系数矩阵的逆阵;KR为桩的无量纲柔度系数，;为桩的侧向位移增量;为土体侧向位移增量，即不考虑桩存在时的土的位移量。

在解答了式（6）后，可以根据桩的弯矩方程式计算压力增量，最后得到总的桩土压力。

（2）李国豪弹性地基梁解答。

假设地基土体水平变位u（z），造成桩体产生的位移为y（z），根据Winkler假定，滑移土体中桩的挠曲方程可写为：

式中，EP为桩的弹性模量，IP为桩的截面惯性矩，b为桩宽。

利用上式求解y（z）时，李国豪取土体的水平位移u（z）为：

式中，λ=π/L，L为桩长，将其代入挠曲方程得：

式中的积分常数A和B用以满足桩顶边界条件。土与桩之间的水平位移之差u（z）-y（z）表示桩土之间作用力的分布情况，它等于：

在两种基于桩土变形理论的分析方法中，李国豪弹性地基梁解答将土体假设为线弹性材料，因此该方法仅适用于土体变形较小的情况;Poulos基于弹性理论的解答，可用于土体大变形计算。

2.3 有限元分析方法

有限元理论的成熟和计算机技术的发展，为有效模拟桩基、土体及相互作用提供了有效手段。该方法可以合理模拟复杂的地质水文环境、边界约束，并可以赋予桩基、土体不同的材料属性，还能够模拟基坑开挖过程中土体、桩基的变形及受力。

近年来，国内外不少专家和学者对基坑开挖过程中桩土相互关系进行了有限元分析，对被动桩的研究提出了有价值的结论，如：Ellis（2001）等基于平面应变有限元分析，建立了软土地基中桥台桩-土的共同作用模型;魏汝龙（1991）等利用二维、三维有限元法，分析了土坡坡度、坡高、填土厚度、桩顶约束条件等因素对码头桩基受力性状的影响，指出二维有限元模型分析在高桩码头桩-土工程问题分析中的适用性。

在有限元分析方法中，ABAQUS在岩土工程领域有很强的适用性，其突出优点是用于非线性问题的求解，能够模拟土体性状的本构关系，如土体的屈服、剪胀性等。ABAQUS提供了线弹性、正交各向异性、多孔结构弹性等弹性模型，而且还提供了Mohr-Coulomb（摩尔库仑）模型、Druker-Prager模型、Cam-Clay模型等塑性模型，能够真实反应土体大部分应力应变特点。ABAQUS还能够准确的模拟土体与结构物之间的接触特性，并具备处理复杂边界及载荷条件的能力等等。在分析过程中，对土体的弹塑性本构关系模拟时，弹性部分可采用线弹性模型，塑性部分采用Mohr-Coulomb模型。

Mohr-Coulomb塑性模型主要适用于在单调载荷下以颗粒为特征的材料，在岩土工程领域有广泛应用，其特点如下：

（1）屈服主应力不受第二主应力σ2大小的影响;

（2）材料是初始各向同性的;

（3）ABAQUS中的Mohr-Coulomb模型，可通过控制凝聚力的大小，实现屈服面的大小变化即硬化或软化;

（4）材料的性质可受温度影响;

（5）Mohr-Coulomb模型不考虑材料率相关性。

屈服准则：

经典Mohr-Coulomb屈服准则认为，当作用在土体某一点处的剪应力等于该点的抗剪强度时，该点发生破坏，其中剪切强度与作用在该面的正应力呈线性关系，即：

式中，τ为剪切强度，c为土体的粘聚力，σ为正应力，φ为土体的内摩擦角。

Mohr-Coulomb破坏模型，基于材料破坏时的应力状态，可由莫尔圆表示，如图2所示，假定了材料的破坏与中主应力无关，因此，在 平面上，Mohr-Coulomb模型为等边不等角的六变形，屈服面存在尖角，与Druker-Prager模型存在不同，如图3所示。

ABAQUS采用的Mohr-Coulomb本构模型是经典Mohr-Coulomb屈服准则的扩展，采用Mohr-Coulomb模型屈服面函数，方程为：

式中，φ是q-p应力面上Mohr-Coulomb屈服面的倾斜角，为材料的摩擦角，p为等效压应力，q为Mises等效应力，c为材料的粘聚力，Rmc（θ，φ）为Mohr-Coulomb偏应力系数，计算式为：

式中，为广义剪应力方位角，定义为，r为第三偏应力不变量。Mohr-Coulomb屈服面在子午面及π面上的形状以及其与Druker-Prager屈服面，Tresca屈服面，Mises屈服面之间的相对关系，如图4所示。

参考文献

[1] 甄晓义.软土地基在堆载作用下被动桩桩土相互作用研究[D].福建：福建农林大学，2019.

[2] 陈璟斌.不同深基坑开挖条件对邻近桩基受力性能影响研究[D].广州：广州大学，2019.

[3] 李明阳.深基坑开挖对桥桩基础变形影响及特性分析[D].福建：华侨大学，2019.

[4] 刘策，宋郁民.基坑开挖对既有小直径桥墩的影响分析及加固设计[J].武汉工程大学学报，2018（6）：649-654.

[5] 孙剑平，唐超，王军，等.堆载致桥梁桩基偏移机理分析与纠偏技術研究[J].建筑结构，2020（6）：61-67.

[6] 林本海，郭乾坤.广州某桥梁桩基偏位的受力性能分析[J].水利与建筑工程学报，2011（4）：55-60，65.

[7] De Beer.Piles Subjected to Static Lateral Loads.Proc.9thICSMFE，Sp.Sess.No.10，1977.

[8] Tomio Ito， et al.Extended Design Method for Multi-Row Stabilizing Piles Against Landslide.Soils and Foundations，Vol.22.No.1，1982.