利用旋转变换解决几何问题

江苏省常州市外国语学校 黄 韦

一、旋转全等变换之1：自旋转模型

例1 已知：在△ABC中，∠BAC＝60°。

（1）如图1，若AB＝AC，点P在△ABC内，且PA＝3，PC＝4，∠APC＝150°，则PB的长为 。

图1

图2

解析：解题的第一步是认真读题。要解题，首先得熟悉题目，弄清已知什么、求什么。这道题目条件简明，但无法将这些条件集中到一起，给解题带来了困难。如图2，将△APC绕着点A逆时针旋转60°到△ADB，由旋转有AD=AP，BD=PC，∠DAB=∠PAC，所以∠DAP=∠BAC=60°，△ADP为等边三角形。由此可以得到DP=PA=3，∠ADP=60°，∠ADB= ∠APC=150°，所以∠BDP=90°，在Rt△BDP中，BD=4，DP=3，根据勾股定理得PB=5。

（2）如图3，若AB＝AC，点P在△ABC外，且PA＝3，PB＝5，PC＝4，则∠APC的度数为 。

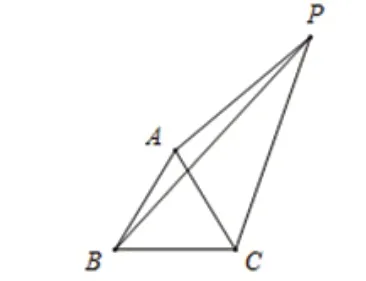
图3

图4

解析：如图4，把△APC绕点A顺时针旋转，使点C与点B重合，得到△ADB，连接PD，可得△DAP是等边三角形，所以PD=3，∠1=60°，由勾股定理逆定理可知△PDB是直角三角形，所以∠PDB=90°，∠APC=30°。

二、旋转全等变换之2：半角模型

半角模型的基本条件是：（1）共端点且相等的线段；（2）共顶点的倍半角；（3）对角互补。半角模型的解题策略是：在半角的旁边再构造一个半角，从而得到两对旋转全等三角形。

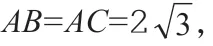
图5

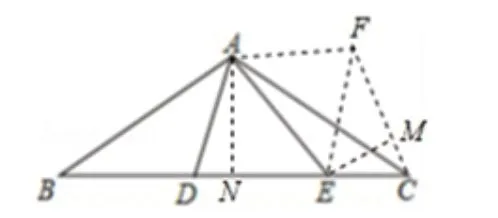
图6

三、旋转全等变换之3：费马旋转60°模型

费马点问题是指解决从同一顶点出发的三条线段和，即“PA+PB+PC”的最小值问题。通常的处理套路是：旋转60°—构造等边三角形—三“折”转一“直”—利用两点之间线段最短—解决问题。

例3 如 图7， △ABC中， ∠ACB=30°，BC=6，AC=5， 在△ABC内部有一点P，连接PA，PB，PC，则PA+PB+PC的最小值为 ___________________。

图7

图8

解析：如图8，∵将△APC绕点C顺时针旋转60°，得到△EDC，∴△APC≌△EDC，

∴∠ACP=∠ECD，AC=EC=5，∠PCD=60°，

∴∠ACP+∠PCB=∠ECD+∠PCB，

∴∠ECD+∠PCB=∠ACB=30°，

∴∠BCE=∠ECD+∠PCB+∠PCD=30°+60°=90°。

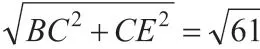
旋转变换是三大几何基本变换之一，它是解决几何问题中的重要手段。当题目给的条件较为分散时，可以依据题意，通过旋转变换，将分散的条件集中起来，从而把复杂问题简单化，便于求解。